6.4 ತ್ರಿಕೋನಗಳು   (Triangles):

 

6.4.1 ತ್ರಿಭುಜಗಳ ವರ್ಗೀಕರಣ ಮತ್ತು ತ್ರಿಭುಜಗಳು ಮೇಲಿನ ಪ್ರಮೇಯಗಳು  (Classification and Theorems on triangles):

 

ತ್ರಿಕೋನ = ತ್ರಿ + ಕೋನ = ಮೂರು ಕೋನಗಳು

ತ್ರಿಭುಜ = ತ್ರಿ + ಭುಜ = ಮೂರು ಭುಜಗಳು

ವ್ಯಾಖ್ಯೆ: ಮೂರು ಖಂಡಗಳಿಂದ ಆವೃತವಾದ ಆಕೃತಿಯೇ ‘ತ್ರಿಕೋನ’ ಅಥವಾ ‘ತ್ರಿಭುಜ’ (Triangle)

ಒಂದು ತ್ರಿಕೋನದಲ್ಲಿ: ಮೂರು ಬಾಹುಗಳಿವೆ :- AB, BC, CA

                              ಮೂರು ಶೃಂಗಬಿಂದುಗಳಿವೆ :- A, B, C

                              ಮೂರು ಕೋನಗಳಿವೆ:-  ABC, BCA, CAB

 

 

ತ್ರಿಭುಜದಲ್ಲಿ ಅಳೆಯಬಹುದಾದದ್ದು ಭುಜಗಳು ಮತ್ತು ಬಾಹುಗಳು ಮಾತ್ರ(ಬಿಂದುವನ್ನು ಅಳೆಯಲು ಸಾಧ್ಯವೇ?)

ತ್ರಿಕೋನದಲ್ಲಿರುವ ಬಾಹುಗಳು ಮತ್ತು ಕೋನಗಳ ಅಳತೆಗಳಿಗನುಗುಣವಾಗಿ ಅವುಗಳನ್ನು ಈ ಕೆಳಗಿನಂತೆ ವರ್ಗೀಕರಿಸಬಹುದು: 

ವರ್ಗೀಕರಣ

ತ್ರಿಕೋನದ ವಿಧ

ಲಕ್ಷಣ

ಉದಾಹರಣೆ ಚಿತ್ರ

ಕೋನಗಳ ಅಳತೆಗೆ ಅನುಸಾರವಾಗಿ

ಲಘುಕೋನ ತ್ರಿಕೋನ

ಪ್ರತಿಯೊಂದು ಕೋನವೂ 900 ಗಿಂತ ಕಡಿಮೆ .

 

ಲಂಬಕೋನ ತ್ರಿಕೋನ

ಒಂದು ಕೋನವು 900

PQR =900

 

ವಿಶಾಲಕೋನ  ತ್ರಿಕೋನ

ಒಂದು ಕೋನವು  900  ಗಿಂತ ಹೆಚ್ಚು (ವಿಶಾಲಕೋನ)

BCA > 900

 

ಸಮಕೋನ ತ್ರಿಕೋನ

ಎಲ್ಲಾ ಕೋನಗಳು ಪರಸ್ಪರ ಸಮ PQR =QRP =RPQ = 600

ಸಮದ್ವಿಕೋನ ತ್ರಿಕೋನ

ಎರಡು ಕೋನಗಳು ಪರಸ್ಪರ ಸಮ ABC =BCA

 

ಬಾಹುಗಳ ಅಳತೆಗೆ ಅನುಸಾರವಾಗಿ

ಅಸಮಬಾಹು ತ್ರಿಕೋನ

ಎಲ್ಲಾ ಬಾಹುಗಳ ಅಳತೆ ಭಿನ್ನ PQ≠QR≠RP

ಬಾಹುಗಳ ಅಳತೆಗೆ ಅನುಸಾರವಾಗಿ

ಸಮಬಾಹು ತ್ರಿಕೋನ

(ಸಮಕೋನ ತ್ರಿಕೋನವು ಹೌದು)

ಎಲ್ಲಾ ಬಾಹುಗಳು ಸರ್ವಸಮ AB=BC=CA

ಬಾಹುಗಳ ಅಳತೆಗೆ ಅನುಸಾರವಾಗಿ

ಸಮದ್ವಿಬಾಹು ತ್ರಿಕೋನ

ಎರಡು ಬಾಹುಗಳು ಸಮ PQ=PR

ಬಾಹುಗಳ ಅಳತೆಗೆ ಅನುಸಾರವಾಗಿ

ಸಮದ್ವಿಬಾಹು ಲಂಬಕೋನ ತ್ರಿಕೋನ

ಲಂಬಕೋನ ತ್ರಿಕೋನದಲ್ಲಿ 2 ಬಾಹುಗಳು ಸರಸ್ಪರ ಸಮ.

ABC =900

 AB=BC


ನಮಗೆ ತ್ರಿಕೋನದ ಮೂರು ಕೋನಗಳ ಮೊತ್ತ 1800 ಎಂದು ತಿಳಿದಿದೆ. ಇದನ್ನು ತಾರ್ಕಿಕವಾಗಿ ಸಾಧಿಸುವುದು ಹೇಗೆ?

 

6.4.1 ಪ್ರಮೇಯ 1:  ಒಂದು ತ್ರಿಕೋನದ ಮೂರು ಕೋನಗಳ ಮೊತ್ತ 1800 ಆಗಿದೆ.

ದತ್ತ: ABC ಯು ಒಂದು ತ್ರಿಕೋನ..

ಸಾಧನೀಯ:  ABC+BAC +ACB = 1800

ರಚನೆ: A ಬಿಂದುವಿನ ಮೂಲಕ ಹಾದು ಹೋಗುವಂತೆ,, BC ಸಮಾಂತರವಾಗಿ DE ರೇಖಾಖಂಡವನ್ನೆಳೆದಿದೆ.

 

ಸಂ.

ನಿರೂಪಣೆ

ಕಾರಣಗಳು

1

EAB =  ABC

DE || BC, AB  ಛೇದಕರೇಖೆ, ಪರ್ಯಾಯ ಕೋನಗಳು .

2

EAC = ACB

DE || BC, AC  ಛೇದಕರೇಖೆ, ಪರ್ಯಾಯ ಕೋನಗಳು .

3

EAB+BAC +EAC= 1800

ಒಂದೇ ಸರಳರೇಖೆಯ ಮೇಲಿನ ಕೋನಗಳು .

4

ABC+BAC +ACB= 1800

3 ರಲ್ಲಿ EAB ಗೆ  ACB ಯನ್ನು EAC ಗೆ  ABC ಯನ್ನು ಆದೇಶಿಸಿದೆ.


6.4.1 ಸಮಸ್ಯೆ 1: ಒಂದು ಸಮದ್ವಿಬಾಹು ತ್ರಿಕೋನದಲ್ಲಿ ಒಂದು ಕೋನ 400 ಆದರೆ ಉಳಿದೆರಡು ಕೋನಗಳನ್ನು ಕಂಡುಹಿಡಿ.

 

ಪರಿಹಾರ:

ಒಂದು ಸಮದ್ವಿಬಾಹು ತ್ರಿಕೋನದಲ್ಲಿ ಎರಡು ಕೋನಗಳು ಪರಸ್ಪರ ಸಮ ಎನ್ನುವುದನ್ನು ಗಮನಿಸಿ(ಮುಂದೆ 6.4.3 ರಲ್ಲಿ ಇದನ್ನು ಸಾಧಿಸಲಿದ್ದೇವೆ). ತ್ರಿಕೋನದ ಮೂರು ಕೋನಗಳ ಮೊತ್ತ 1800.

ಎರಡು ಸಾಧ್ಯತೆಗಳಿವೆ:

1 ಪರಸ್ಪರ ಸಮವಿರುವ ಪ್ರತೀ ಕೋನ  x ಆಗಿರಲಿ. ಮೂರನೇ ಕೋನ 400

ಆಗ, x + x + 400 = 1800  

2x =1800 - 400  = 1400

 x = 700

ತ್ರಿಕೋನದ ಮೂರು ಕೋನಗಳು: 700,700 ಮತ್ತು 400.

 

2)  ಪರಸ್ಪರ ಸಮವಿರುವ ಪ್ರತೀ ಕೋನ 400 ಆಗಿರಲಿ. ಮೂರನೇ ಕೋನ x ಆಗಿರಲಿ

ಆಗ, 400 + 400 + x = 1800  

800 + x = 1800

 x = 1000

ತ್ರಿಕೋನದ ಮೂರು ಕೋನಗಳು: 400,400 ಮತ್ತು 1000.

 

6.4.1 ಸಮಸ್ಯೆ 2: ಸಮಕೋನೀಯ (ಸಮಬಾಹು) ತ್ರಿಕೋನದ ಕೋನಗಳನ್ನು ಕಂಡುಹಿಡಿ.

 

ಪರಿಹಾರ:

ಒಂದು ಸಮಕೋನೀಯ (ಸಮಬಾಹು) ತ್ರಿಕೋನದಲ್ಲಿ ಮೂರು ಕೋನಗಳು ಪರಸ್ಪರ ಸಮ. ತ್ರಿಕೋನದ ಮೂರು ಕೋನಗಳು ಮೊತ್ತ 1800.

ಆದ್ದರಿಂದ, ಸಮಬಾಹು ತ್ರಿಕೋನದ ಒಂದು ಕೋನ x ಆಗಿದ್ದರೆ,

x + x + x = 1800  

3x =1800

 x = 600.

 

ವ್ಯಾಖ್ಯೆ:

ತ್ರಿಭುಜದ ಯಾವುದೇ ಬಾಹುವನ್ನು ವೃದ್ಧಿಸಿದಾಗ, ಶೃಂಗದಲ್ಲಿ ಉಂಟಾಗುವ ಕೋನವನ್ನು ‘ಬಹಿರ್‍ಕೋನ’ (exterior) ಎನ್ನುತ್ತೇವೆ. ಚಿತ್ರದಲ್ಲಿ  ACD ಯು ಬಹಿರ್‍ಕೋನ.

ಬಹಿರ್‍ಕೋನದ ಪಕ್ಕದಲ್ಲಿರುವ ಕೋನದ ಎದುರು, ತ್ರಿಕೋನದ ಒಳಭಾಗದಲ್ಲಿ ಇರುವ ಎರಡು ಕೋನಗಳನ್ನು ‘ಅಂತರಾಭಿಮುಖ ಕೋನಗಳು’ (interior opposite angles) ಎನ್ನುವರು. ಚಿತ್ರದಲ್ಲಿ  BAC ಮತ್ತು ABC

ಗಳು ಅಂತರಾಭಿಮುಖ ಕೋನಗಳು

 

 

 

ಚಿತ್ರ

ಬಹಿರ್‍ಕೋನ

ಅಂತರಾಭಿಮುಖ ಕೋನ

k

 

ACD

 

ಇಲ್ಲಿ ಬಹಿರ್‍ಕೋನವು ವಿಶಾಲಕೋನವಾಗಿದೆ (ACD > 900)

 

BAC ಮತ್ತು ABC

CBD

 

ಇಲ್ಲಿ ಬಹಿರ್‍ಕೋನವು ಲಘುಕೋನವಾಗಿದೆ (CBD < 900)

 

BAC ಮತ್ತು ACB

ABD

 

ಇಲ್ಲಿ ಬಹಿರ್‍ಕೋನವು ಲಂಬಕೋನವಾಗಿದೆ  (ABD =900)

 

BAC ಮತ್ತು BCA

 

ಗಮನಿಸಿ: ತ್ರಿಕೋನದಲ್ಲಿ 3 ಬಾಹುಗಳಿರುವುದರಿಂದ, ಮೂರು ಬಹಿರ್‍ಕೋನಗಳಿರುತ್ತವೆ.

 

6.4.1 ಪ್ರಮೇಯ 2: ಒಂದು ತ್ರಿಕೋನದ ಒಂದು ಬಾಹುವನ್ನು ವೃದ್ಧಿಸಿದಾಗ ಉಂಟಾಗುವ ಬಹಿರ್‍ಕೋನವು ಅಂತರಾಭಿಮುಖ ಕೋನಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮವಾಗಿರುತ್ತದೆ.

ದತ್ತ: ABC ತ್ರಿಕೋನದಲ್ಲಿ BC ಬಾಹುವನ್ನು D ವರೆಗೆ ವೃದ್ಧಿಸಿದೆ.

ಸಾಧನೀಯ ACD = ABC + BAC

ಸಾಧನೆ:

ಸಂ.

ನಿರೂಪಣೆ

ಕಾರಣಗಳು

 

1

ABC+BCA +CAB = 1800

ಪ್ರಮೇಯ : ತ್ರಿಕೋನದ 3 ಕೋನಗಳ ಮೊತ್ತ = 1800

2

BCA+ACD = 1800

ಸರಳಯುಗ್ಮ ಕೋನಗಳು

3

ABC+BCA +BAC =

BCA+ACD

ಸ್ವಯಂಸಿದ್ಧ1

4

ABC + BAC= ACD

ಸ್ವಯಂಸಿದ್ಧ 2, BCAಯನ್ನು ಕಳೆದಿದೆ

 

ಗಮನಿಸಿ:

ಸಂ.

ಮೇಲಿನೆರಡು ಪ್ರಮೇಯಗಳ ಉಪ ಪ್ರಮೇಯಗಳು

ಕಾರಣಗಳು (x,y,z ಗಳು ತ್ರಿಕೋನದ 3 ಕೋನಗಳಾಗಿರಲಿ

1

ಬಹಿರ್‍ಕೋನವು ಪ್ರತಿಯೊಂದು ಅಂತರಾಭಿಮುಖ ಕೋನಕ್ಕಿಂತಲೂ ದೊಡ್ಡದು.

ಬಹಿರ್‍ಕೋನ = x+y: x,y > 0 ಆದಾಗ, x+y >x, x+y > y

2

ಒಂದು ತ್ರಿಕೋನದಲ್ಲಿ ಒಂದಕ್ಕಿಂತ ಹೆಚ್ಚು ಲಂಬ ಕೋನಗಳಿರಲು ಸಾಧ್ಯವಿಲ್ಲ.

x+y+z =180 ಆದಾಗ,  x ಮತ್ತು y ಗಳೆರಡೂ 90 ಆಗಲು ಸಾಧ್ಯವಿಲ್ಲ.

3

ಒಂದು ತ್ರಿಕೋನದಲ್ಲಿ ಒಂದಕ್ಕಿಂತ ಹೆಚ್ಚು ವಿಶಾಲ ಕೋನಗಳಿರಲು ಸಾಧ್ಯವಿಲ್ಲ

x>90 ಆದಾಗ, y+z <90 ಆಗಿರುತ್ತದೆ.

4

ಯಾವುದೇ ತ್ರಿಕೋನದಲ್ಲಿ ಕನಿಷ್ಟ 2 ಕೋನಗಳು ಲಘು ಕೋನಗಳಾಗಿರುತ್ತವೆ.

x < 90 ಆದಾಗ, y, zಗಳೆರಡೂ90 ಕ್ಕಿಂತ ಹೆಚ್ಚಿರಲು ಸಾಧ್ಯವಿಲ್ಲ.

5

ಒಂದು ಲಂಬಕೋನ ತ್ರಿಕೋನದಲ್ಲಿ ಉಳಿದೆರಡು ಕೋನಗಳ ಮೊತ್ತ = 900

x=90 ಆದಾಗ, x+y+z = 180 ಆದ್ದರಿಂದ y+z = 90 ಆಗಿರಲೇಬೇಕು

6

ಒಂದು ತ್ರಿಕೋನದ 2 ಕೋನಗಳು ಇನ್ನೊಂದು ತ್ರಿಕೋನದ 2 ಕೋನಗಳಿಗೆ ಸಮವಾಗಿದ್ದರೆ. ಆ ಎರಡೂ ತ್ರಿಕೋನಗಳ 3ನೇ ಕೋನಗಳು ಸಮವಾಗಿರುತ್ತವೆ.

x+y+z = 180,  a+b+c = 180 ಮತ್ತು x=a, y=b  ಆದರೆ

z =c ಆಗಿರಲೇಬೇಕು.

 

6.4.1 ಸಮಸ್ಯೆ 3:  ಒಂದು ತ್ರಿಕೋನದ ಒಂದು ಬಹಿರ್‍ಕೋನವು 900 ಆಗಿದ್ದು, ಒಂದು ಅಂತರಾಭಿಮುಖ ಕೋನ 450 ಆದರೆ ತ್ರಿಕೋನದ ಉಳಿದೆರಡು ಕೋನಗಳನ್ನು ಕಂಡುಹಿಡಿ.

 

ಪರಿಹಾರ:

ದತ್ತ: ಒಂದು ಅಂತರಾಭಿಮುಖ ಕೋನ 450.

ಇನ್ನೊಂದು ಅಂತರಾಭಿಮುಖ ಕೋನ = x ಆಗಿರಲಿ

ಕೋನದ ಬಹಿರ್‍ಕೋನ = ಅಂತರಾಭಿಮುಖ ಕೋನಗಳ ಮೊತ್ತ

900 = x+450

x = 450.

 

6.4.1 ಸಮಸ್ಯೆ 4:   ಕೆಳಗೆ ಕೊಟ್ಟ ತ್ರಿಕೋನದ ಎಲ್ಲಾ ಕೋನಗಳನ್ನು ಕಂಡುಹಿಡಿ.

ಪರಿಹಾರ:

p+q = 1000  ------(1)

r+q = 1300   ------(2)

p + q + r = 1800    ಆಗಿದೆ

1000 + r = 1800

 r = 1800-1000=800

ಆದೇಶಗಳಿಂದ q= 500 ,p= 500.

ತ್ರಿಕೋನದ ಕೋನಗಳು 500 (=p) 500 (=q) ಮತ್ತು 800(=r)  ಆಗಿವೆ.

 

6.4.1 ಸಮಸ್ಯೆ 5:  ಒಂದು ಚತುರ್ಭುಜದ ನಾಲ್ಕು ಕೋನಗಳ ಮೊತ್ತ  3600 ಎಂದು ಸಾಧಿಸಿ.

 

ಪರಿಹಾರ:

ಯಾವುದೇ ಚತುರ್ಭುಜದಲ್ಲಿ ಒಂದು ಕರ್ಣವನ್ನೆಳೆದಾಗ, ಅದು 2 ತ್ರಿಭುಜಗಳಾಗಿ ವಿಭಾಗವಾಗುತ್ತದೆ.

ಯಾವುದೇ ತ್ರಿಕೋನದ 3 ಕೋನಗಳ ಮೊತ್ತ 1800

* ಚತುರ್ಭುಜದ ನಾಲ್ಕು ಕೋನಗಳ ಮೊತ್ತ = 2*(ಪ್ರತಿ ತ್ರಿಕೋನದ ಕೋನಗಳ ಮೊತ್ತ)

                                                     = 2*1800 =3600

 

 

6.4.1 ಸಮಸ್ಯೆ 6:  ABC ಯಲ್ಲಿ, 2(A-20) = B+10= 2(C-10) ಆದರೆ ಪ್ರತಿ ಕೋನವನ್ನು ಕಂಡುಹಿಡಿ.

 

ಪರಿಹಾರ:

A+B+C =180 ಆದ್ದರಿಂದ  B = 180-C-A

2(A-20) = B+10  ==== ದತ್ತ

2A-40 =B+10

2A = B+50 = (180-C-A)+50 = 230 –C –A. 

3A = 230-C ------(1)

2(A-20) = 2(C-10) ==== ದತ್ತ

A-20  = C-10

A = C+10         ==== (2)

A ಯ ಬೆಲೆಯನ್ನು ಸಮೀಕರಣ (1)ರಲ್ಲಿ ಆದೇಶಿಸಿದಾಗ,

3A = 3C+ 30 =230-C 4C = 200 C = 50

ಯ ಬೆಲೆಯನ್ನು ಸಮೀಕರಣ  (2)ರಲ್ಲಿ ಆದೇಶಿಸಿದಾಗ, A =60.

A+B+C = 180  B = 70

 ಕೋನಗಳು A = 60, B=70,C=50.

 

 

 

6.4.1 ಸಮಸ್ಯೆ 7:   ಒಂದು ವಜ್ರಾಕೃತಿಯ ಯಾವುದೇ ಎರಡು ಕೋನಗಳ ಕೋನಾರ್ಧಕ ರೇಖೆಗಳು ಲಂಬಕೋನ ತ್ರಿಕೋನವನ್ನುಂಟು ಮಾಡುತ್ತವೆ ಎಂದು ಸಾಧಿಸಿ

ಸಾಧಿಸಬೇಕಾದದ್ದು: POQ = 900.

ಸಾಧನೆ:

ಸಂ.

ನಿರೂಪಣೆ

ಕಾರಣಗಳು

 

1

SPQ+PQR =1800

PQRS ಒಂದು ವಜ್ರಾಕೃತಿ.  PS||QR

ಆಗ ಅಂತರ್‍ಕೋನಗಳು ಪರಿಪೂರಕ.

2

2(OPQ+PQO) = 1800

PO ಮತ್ತು QO ಗಳು ಕೋನಾರ್ಧಕ ರೇಖೆಗಳು          

3

OPQ+PQO = 900

ಹಂತ 2

4

POQ = 180- (OPQ+PQO) = 900

 

 

6.4.2 ತ್ರಿಭುಜಗಳ ರಚನೆ (Construction of Triangles):

 

ತ್ರಿಕೋನದಲ್ಲಿ ಮೂರು ಬಾಹುಗಳಿವೆ ಮತ್ತು ಕೋನಗಳಿವೆ. ಒಟ್ಟು 6 ಭಾಗಗಳಿವೆ. ಆದರೆ ಒಂದು ತ್ರಿಭುಜವನ್ನು ರಚಿಸಲು ಈ ಆರೂ ಅವಯವಗಳು ಬೇಕಾಗುವುದಿಲ್ಲ. ಬದಲಾಗಿ ಬರೇ ಮೂರು ಅವಯವಗಳು ಸಾಕು. ಆದರೆ ಅದರಲ್ಲಿ ಕನಿಷ್ಟ ಒಂದಾದರೂ ಬಾಹು ಆಗಿರಬೇಕು.

 

6.4.2.1. ಮೂರು ಬಾಹುಗಳನ್ನು ಕೊಟ್ಟಾಗ ತ್ರಿಭುಜದ ರಚನೆ (Construction of a triangle when 3 sides are given):

 

6.4.2 ಸಮಸ್ಯೆ 1: AB = 3 ಸೆಂ.ಮಿ. BC = 4 ಸೆಂ.ಮಿ. ಸೆಂ.ಮಿ.  AC = 5 ಸೆಂ.ಮಿ. ABC ಇರುವಂತೆ ತ್ರಿಭುಜವನ್ನು ರಚಿಸಿ.

 

ರಚನಾ ಕ್ರಮ:

ಮೊತ್ತಮೊದಲಿಗೆ ABC ತ್ರಿಕೋನದ ಕರಡು ಚಿತ್ರ ರಚಿಸಿ.

1)3 ಸೆಂ.ಮಿ ಉದ್ದದ AB ಸರಳರೇಖೆಯನ್ನೆಳೆಯಿರಿ(ಕಂಸದ ಸಹಾಯದಿಂದ)

2) A ಯನ್ನು ಕೇಂದ್ರವಾಗಿಟ್ಟುಕೊಂಡು 5 ಸೆಂ.ಮಿ. ತ್ರಿಜ್ಯದಿಂದ ಒಂದು ಕಂಸವನ್ನೆಳೆಯಿರಿ.

3) B ಯನ್ನು ಕೇಂದ್ರವಾಗಿಟ್ಟುಕೊಂಡು 4 ಸೆಂ.ಮಿ. ತ್ರಿಜ್ಯದಿಂದ  ಮೇಲೆ ಎಳದ ಕಂಸವನ್ನು C ಯಲ್ಲಿ ಕಡಿಯುವಂತೆ ಇನ್ನೊಂದು  ಕಂಸವನ್ನೆಳೆಯಿರಿ.

4) AC ಮತ್ತು BC ಗಳನ್ನು ಜೋಡಿಸಿ. ABC ಯು ನಮಗೆ ಬೇಕಾದ ತ್ರಿಕೋನ.      

 

6.4.2 ಸಮಸ್ಯೆ 2: ಒಂದು ಮೈದಾನವು ಸಮಬಾಹು ತ್ರಿಭುಜಾಕೃತಿಯಲ್ಲಿದೆ. ಅದರ ಸುತ್ತಳತೆ 2490ಮೀಟರ್‍ಗಳು. ಸೂಕ್ತವಾದ ಅಳತೆಗನುಸಾರವಾಗಿ ಮೈದಾನದ ಚಿತ್ರ ರಚಿಸಿರಿ.

 

ಪರಿಹಾರ:

ತ್ರಿಕೋನದ ಸುತ್ತಳತೆಯು ಅದರ ಮೂರು ಬಾಹುಗಳ ಮೊತ್ತವಾಗಿದೆ. ಮೈದಾನವು ಸಮಬಾಹು ತ್ರಿಕೋನಾಕೃತಿಯಲ್ಲಿರುವುದರಿಂದ ಅದರ ಎಲ್ಲಾ ಬದಿಗಳು ಸರ್ವಸಮ.

3 ಬದಿ = 2490 ಮಿ.  ಬದಿ = 2490/3 = 830 ಮಿ.

ಈಗ = 830 ಮಿ. ಬದಿಯುಳ್ಳ ತ್ರಿಕೋನ ರಚಿಸಲು ಸಾಧ್ಯವಿಲ್ಲ. ಅದಕ್ಕಾಗಿ ಸೂಕ್ತ ಪ್ರಮಾಣ ಇಟ್ಟುಕೊಳ್ಳುವಾ. 100ಮಿ. = 1ಸೆಂ.ಮಿ. ಆಗ ನಾವು ರಚಿಸಬೇಕಾದ್ದು = 8.3ಸೆಂ.ಮಿ. ಬಾಹುವುಳ್ಳ ಸಮಬಾಹು ತ್ರಿಭುಜ.

ಸಮಾಂತರ ತ್ರಿಭುಜದ ಎಲ್ಲಾ ಬಾಹುಗಳು ಸಮವಾದ್ದರಿಂದ ತ್ರಿಕೋನದ ಮೂರು ಬಾಹುಗಳು 8.3ಸೆಂ.ಮಿ., 8.3ಸೆಂ.ಮಿ. ಮತ್ತು 8.3ಸೆಂ.ಮಿ.

ಅಭ್ಯಾಸ: 6.4.2.1(ಹಿಂದಿನ) ಸಮಸ್ಯೆಯಂತೆಯೇ ಈ ತ್ರಿಭುಜವನ್ನು ರಚಿಸಿ.

 

 

 

6.4.2.2. ಎರಡು ಬಾಹುಗಳು ಮತ್ತು ಅವುಗಳ ನಡುವಿನ ಕೋನವನ್ನು ಕೊಟ್ಟಾಗ ತ್ರಿಭುಜದ ರಚನೆ (Construction of a triangle when 2 sides and an included angle are given)

 

6.4.2 ಸಮಸ್ಯೆ 3: AB = 3ಸೆಂ.ಮಿ., BC = 4 ಸೆಂ.ಮಿ ಮತ್ತು ABC =1200 ಇರುವಂತೆ ABC ತ್ರಿಭುಜವನ್ನು ರಚಿಸಿ. 

ರಚನಾ ಕ್ರಮ:

ಮೊತ್ತ ಮೊದಲಿಗೆ ABC ತ್ರಿಭುಜದ  ಕರಡು ಚಿತ್ರ ರಚಿಸಿ

A ಬಿಂದುವನ್ನು ಗುರುತಿಸಿ ಅಲ್ಲಿಂದ  ಒಂದು ಸರಳ ರೇಖೆ ಎಳೆದು 3 ಸೆಂ.ಮಿ ದೂರದಲ್ಲಿ(ಕಂಸದ ಮೂಲಕ)

B ಬಿಂದುವನ್ನು ಗುರುತಿಸಿ

B ಯಿಂದ  ಕೋನಮಾಪಕದ ಮೂಲಕ 1200 ಆಗುವಂತೆ ಒಂದು ಸರಳ ರೇಖೆ ಎಳೆಯಿರಿ.

B ಕೇಂದ್ರವಾಗಿಟ್ಟುಕೊಂಡು,4 ಸೆಂ.ಮಿ ಕಂಸದಿಂದ ಮೇಲಿನ ರೇಖೆನ್ನು C ಯಲ್ಲಿ ಕಡಿಯಿರಿ.

AC ಜೋಡಿಸಿದೆ. ABC ಯು ನಮಗೆ ಬೇಕಾದ ತ್ರಿಕೋನ.

 

 

ಗಮನಿಸಿ: ಲಂಬಕೋನ ತ್ರಿಕೋನದಲ್ಲಿ 2 ಬಾಹುಗಳನ್ನು ಕೊಟ್ಟಾಗ ಇದೇ ಕ್ರಮವನ್ನು ಅನುಸರಿಸಿ ತ್ರಿಕೋನವನ್ನು ರಚಿಸುತ್ತೇವೆ.

 

 

6.4.3 ತ್ರಿಕೋನಗಳ ಸರ್ವಸಮತೆ (Congruency of Triangles):

 

ಅದೇ ರೀತಿ, ನೀರಿಗಿಳಿಯದೆ ಒಂದು ನದಿಯ ಅಗಲವನ್ನು ಅಳೆಯುವುದು ಹೇಗೆ? ದಿನನಿತ್ಯದ ಇಂತಹ ಸಮಸ್ಯೆಗಳಿಗೆ ರೇಖಾಗಣಿತದಲ್ಲಿ ಪರಿಹಾರವಿದೆ.

ರೇಖಾಗಣಿತದಲ್ಲಿ ಎರಡು ಆಕೃತಿಗಳು ಎಲ್ಲಾ ವಿಧದಲ್ಲೂ ಒಂದಕ್ಕೊಂದು ಸಮವಾಗಿದ್ದರೆ, ಅವುಗಳನ್ನು ಸರ್ವಸಮ ಆಕೃತಿಗಳು ಎನ್ನುತ್ತೇವೆ. (ಎರಡು ರೇಖಾಗಣಿತ ಸಮತಲಾಕೃತಿಗಳನ್ನು ಒಂದರಲ್ಲಿ ಇನ್ನೊಂದು ಐಕ್ಯವಾಗುವಂತೆ ಇಡಲು ಸಾಧ್ಯವಾದರೆ. ಅವುಗಳನ್ನು ಸರ್ಮಸಮ ಎನ್ನುತ್ತೇವೆ.)

 

ಎರಡು ಸರಳರೇಖೆಗಳ ಉದ್ದಗಳು ಸಮವಾಗಿದ್ದರೆ, ಅವು ಸರ್ವಸಮ. 

ಎರಡು ಕೋನಗಳು ಒಂದೇ ಅಳತೆಯವುಗಳಾಗಿದ್ದರೆ, ಅವು ಸರ್ವಸಮ.

ಎರಡು ತ್ರಿಕೋನಗಳಲ್ಲಿ ಸಮವಾಗಿರುವ ಕೋನಗಳಿಗೆ ಅಭಿಮುಖವಾಗಿರುವ ಬಾಹುಗಳೇ ಅನುರೂಪ ಬಾಹುಗಳು (corresponding sides).ಎರಡು ಸರ್ವಸಮ ತ್ರಿಕೋನಗಳಲ್ಲಿ ಸಮವಾಗಿರುವ ಎರಡು ಬಾಹುಗಳಿಗೆ ಅಭಿಮುಖವಾಗಿರುವ ಕೋನಗಳು ಅನುರೂಪ ಕೋನಗಳು (corresponding angles).

ಚಿತ್ರ 3 ರಲ್ಲಿ AC ಮತ್ತು DF, AB ಮತ್ತು E, BC ಮತ್ತು ED ಅನುರೂಪಬಾಹುಗಳು. ABC ಮತ್ತು DEF, ACB ಮತ್ತು EDF, CAB ಮತ್ತು EFD ಗಳು ಅನುರೂಪ ಕೋನಗಳು. ಎರಡು ತ್ರಿಕೋನಗಳಲ್ಲಿ ಒಂದರ ಮೂರು ಬಾಹುಗಳು ಮತ್ತು 3 ಕೋನಗಳು ಇನ್ನೊಂದರ 3  ಅನುರೂಪಬಾಹುಗಳಿಗೆ ಮತ್ತು ಅನುರೂಪಕೋನಗಳಿಗೆ ಸಮವಾಗಿದ್ದರೆ, ಅವು ಸರ್ವಸಮ (congruent).

ಚಿತ್ರ 1 : AB=CD=3 ಸೆಂ.ಮಿ.

ಚಿತ್ರ 2  : ABC =FDE = 600

ಚಿತ್ರ 3: AC=DF,AB=EF BC=ED, CAB =EFD, ABC=DEF, ACB=EDF

ಸರ್ವಸಮತೆಯನ್ನು ಚಿಹ್ನೆ   ಯಿಂದ ಸೂಚಿಸುತ್ತೇವೆ.

ಚಿತ್ರ 1 : ABCD

ಚಿತ್ರ 2  : ABCFDE

ಚಿತ್ರ 3: ABCDEF

 

ಗಮನಿಸಿ: ಎರಡು ಸರ್ವಸಮ ತ್ರಿಕೋನಗಳು ಒಂದರಲ್ಲೊಂದು ಸಂಪೂರ್ಣ ಐಕ್ಯವಾಗುವಂತೆ ಇರುವುದರಿಂದ ಅವುಗಳ ವಿಸ್ತೀರ್ಣಗಳು ಸಮವಾಗಿರುತ್ತವೆ.

 

6.4.3 ಉದಾ 1: ಎರಡು ತ್ರಿಕೋನದಲ್ಲಿ ಒಟ್ಟು 6 ಅವಯವಗಳು (3 ಬಾಹುಗಳು ಮತ್ತು 3 ಕೋನಗಳು) ಇದ್ದರೂ ಸಹ, ನಾವೀಗ ಕೆಳಗೆ ಕೊಟ್ಟಿರುವ  ಮೂರು ಅಳತೆಗಳಿಂದ ABC ತ್ರಿಭುಜವನ್ನು ರಚಿಸುವಾ:

1.  BC = 4 ಸೆಂ.ಮಿ., CA = 4.5 ಸೆಂ.ಮಿ., BA= 5 ಸೆಂ.ಮಿ.

2.  BC = 3 ಸೆಂ.ಮಿ., ABC =400, BCA =500

3.  BC = 5 ಸೆಂ.ಮಿ., CA=6 ಸೆಂ.ಮಿ., BCA = 600

4,5.  ಒಂದು ತ್ರಿಕೋನದ ಮೂರು ಕೋನಗಳು 600, 500, 700

 

                        

 

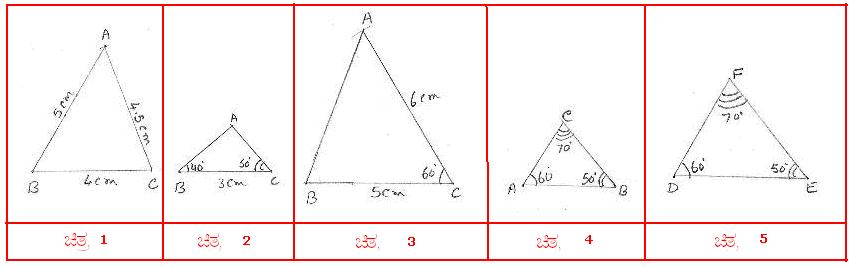
ಗಮನಿಸಿ: ತ್ರಿಕೋನದ 3 ಕೋನಗಳನ್ನು ಕೊಟ್ಟಾಗ ನಾವು ಹಲವಾರು ತ್ರಿಕೋನಗಳನ್ನು ರಚಿಸಬಹುದು:

(ಚಿತ್ರ 4 ಮತ್ತು ಚಿತ್ರ 5 ರಲ್ಲಿ ಅನುರೂಪ ಕೋನಗಳು ಸಮವಾಗಿದ್ದರೂ ಸಹ, AB ≠ DE, BC ≠ FE, AC ≠ DF) 

 

ತೀರ್ಮಾನ: ಕೆಳಗೆ ಕೊಟ್ಟಿರುವ ಮೂರು ಅಂಶಗಳಿಂದ ನಾವು ಏಕೈಕ (Unique) ತ್ರಿಭುಜಗಳನ್ನು ರಚಿಸಬಹುದು..

1.      ಮೂರು ಬಾಹುಗಳು

2.      ಒಂದು ಬಾಹು ಮತ್ತು 2 ಕೋನಗಳು

3.      ಎರಡು ಬಾಹುಗಳು ಮತ್ತು ಅವುಗಳ ನಡುವಿನ ಕೋನ.

 

ತಃಖ್ತೆ A: ನಾವು ಕಂಡುಕೊಂಡ ವಿಷಯಗಳನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಹೀಗೆ ಪಟ್ಟಿ ಮಾಡಬಹುದು:

ಬಾಹು

ಬಾಹು

ಬಾಹು

ಕೋನ

ಕೋನ

ಕೋನ

ಫಲಿತಾಂಶ

Y

Y

Y

-

-

-

ಏಕೈಕ ತ್ರಿಭುಜವನ್ನು ರಚಿಸಬಹುದು.

Y

-

-

Y

Y

-

ಏಕೈಕ ತ್ರಿಭುಜವನ್ನು ರಚಿಸಬಹುದು.

Y

Y

-

Y

-

-

ದತ್ತ ಕೋನವು ದತ್ತ ಬಾಹುಗಳ ನಡುವಿನ ಕೋನವಾಗಿದ್ದರೆ,

ಏಕೈಕ ತ್ರಿಭುಜವನ್ನು ರಚಿಸಬಹುದು.

-

-

-

Y

Y

Y

ಹಲವಾರು ತ್ರಿಭುಜಗಳನ್ನು ರಚಿಸಬಹುದು (ಏಕೈಕ ತ್ರಿಭುಜ ಸಾಧ್ಯವಿಲ್ಲ)

 

ಗಮನಿಸಿ:

1.      ತ್ರಿಕೋನದ 3 ಕೋನಗಳ ಮೊತ್ತ 1800. ಆದ್ದರಿಂದ 2 ಕೋನಗಳನ್ನು ಕೊಟ್ಟಾಗ 3 ನೇ ಕೋನವನ್ನು ಕಂಡು ಹಿಡಿಯಬಹುದು.

2.      ಸರ್ವಸಮತೆಯ ವ್ಯಾಖ್ಯೆಯಂತೆ, ಎರಡು ತ್ರಿಕೋನಗಳು ಸರ್ವಸಮವಾಗಲು ಎರಡೂ ತ್ರಿಕೋನಗಳ 3  ಬಾಹುಗಳು ಮತ್ತು 3  ಕೋನಗಳು ಸಮವಾಗಿರಬೇಕು. ಆದರೆ ನಾವು ತ್ರಿಕೋನಗಳನ್ನು ಏಕೈಕ ರೀತಿಯಲ್ಲಿ  ರಚಿಸಲು 6 ಅಂಶಗಳು ಬೇಕಿಲ್ಲ, ಬರೇ 3  ಅಂಶಗಳು ಸಾಕು ಎಂಬುದನ್ನು 6.4.2 ರಲ್ಲಿ ನೋಡಿದ್ದೇವೆ ಮತ್ತು ಯಾವ ಯಾವ ಸಂದರ್ಭಗಳಲ್ಲಿ ತ್ರಿಕೋನ ರಚಿಸಬಹುದೆಂದು ಮೇಲೆ ತಃಖ್ತೆ ಮಾಡಿದ್ದೇವೆ.

 

ನಾವು ಈಗಾಗಲೇ ನೋಡಿದಂತೆ, ಒಂದು ತ್ರಿಕೋನದ ಎರಡು ಬಾಹುಗಳು ಮತ್ತು ಅವುಗಳ ನಡುವಿನ ಕೋನವನ್ನು ಕೊಟ್ಟಾಗ ಏಕೈಕ ತ್ರಿಭುಜ ರಚಿಸಬಹುದೆಂದು ನೋಡಿದ್ದೇವೆ. ಆದ್ದರಿಂದ, ಎರಡು ತ್ರಿಕೋನಗಳಲ್ಲಿ ಒಂದರ ಎರಡು ಬಾಹುಗಳು ಮತ್ತು ಅವುಗಳಿಂದ ಏರ್ಪಟ್ಟ ಕೋನವು ಸಮವಾಗಿದ್ದರೆ, ಆ ಎರಡು ತ್ರಿಕೋನಗಳ ಸರ್ವಸಮತೆಯ ಬಾ.ಕೋ.ಬಾ. (ಬಾಹು, ಕೋನ, ಬಾಹು) ಸ್ವಯಂಸಿದ್ಧ ಎನ್ನುತ್ತೇವೆ.

 

6.4.3 ಸಮಸ್ಯೆ 1: ಒಂದು ಕೊಳದ ಅಗಲವನ್ನು ಅಳೆಯುವುದು: ಕೆಳಗಿನ ಕೊಳದ ಅಗಲವನ್ನು ಕಂಡುಹಿಡಿ. 

ಪರಿಹಾರ:

ಕೊಳದ ಎರಡೂ ಬದಿಗಳಲ್ಲಿ ಎರಡು ಕಂಬಗಳನ್ನು (A, B ಗಳು) ಸ್ಥಾಪಿಸಿ. ಕೊಳದ ಎದುರು ಭಾಗದಲ್ಲಿ A, B ಗಳು ಸ್ಪಷ್ಟವಾಗಿ ಕಾಣಿಸುವಂತೆ ಅ ಕಂಬವನ್ನು ಸ್ಥಾಪಿಸಿ.

AC=CE ಆಗುವಂತೆ AC ಯನ್ನು E ವರೆಗೆ ವೃದ್ಧಿಸಿ.

BC=CD ಆಗುವಂತೆ BC ಯನ್ನುD ವರೆಗೆ ವೃದ್ಧಿಸಿ.

ಆಗ ACB = DCE (ಶೃಂಗಾಭಿಮುಖ ಕೋನಗಳು)

ಆಗ, ಬಾ.ಕೋ.ಬಾ. ಸ್ವಯಂ ಸಿದ್ಧದಂತೆ, ABC  DEC

AB=DE

DE ಯ ಉದ್ದವು ಕೊಳದ ಅಗಲವನ್ನು ಸೂಚಿಸುತ್ತದೆ.  

 

6.4.3 ಸಮಸ್ಯೆ 2: ಪಕ್ಕದ ಚಿತ್ರದಲ್ಲಿ PQRS ಒಂದು ವರ್ಗ PQ ದ ಮಧ್ಯ ಬಿಂದು, SM=RM ಎಂದು ಸಾಧಿಸಿ.

 

ಪರಿಹಾರ:

PQRS ಒಂದು ವರ್ಗ. ಆದ್ದರಿಂದ  PS=QR, SPQ =900  & PQR = 900 (SPQ = PQR )

PQ ದ ಮಧ್ಯ ಬಿಂದು M ಆದ್ದರಿಂದ, PM=MQ.

ಆದ್ದರಿಂದ ತ್ರಿಕೋನ SPM ಮತ್ತು MQR ಗಳಲ್ಲಿ ಎರಡು ಬಾಹುಗಳು ಮತ್ತು ಅವುಗಳಿಂದ ಏರ್ಪಟ್ಟ ಕೋನಗಳು ಸಮವಾಗಿದೆ.

 

ಆದ್ದರಿಂದ, SPM  MQR

ತ್ರಿಕೋನಗಳ 3ನೇ ಬಾಹುಗಳು SM ಮತ್ತು MR ಗಳು ಪರಸ್ಪರ ಸಮ.

 

 

ಚಟುವಟಿಕೆ: AB=4 ಸೆಂ.ಮಿ., AC=BC=5 ಸೆಂ.ಮಿ. ಇರುವಂತೆ ಒಂದು ತ್ರಿಕೋನವನ್ನು ರಚಿಸಿ.

CAB ಮತ್ತು ABC ಗಳನ್ನು ಅಳೆಯಿರಿ.

ನೀವೇನು ಗಮನಿಸುವಿರಿCAB =ABC?

 

ಫಲಿತಾಂಶ:

ಒಂದು ತ್ರಿಕೋನದಲ್ಲಿ ಸಮವಾದ 2 ಬಾಹುಗಳಿಗೆ ಅಭಿಮುಖವಾಗಿರುವ ಕೋನಗಳು ಸಮವಾಗಿರುತ್ತವೆ.

ಇದನ್ನು ಈಗ ಗಣಿತಶಾಸ್ತ್ರ ರೀತಿಯಲ್ಲಿ ಸಾಧಿಸುವಾ.    

 

6.4.3 ಪಾದ – ಕೋನ ಪ್ರಮೇಯ:

ಒಂದು ತ್ರಿಕೋನದಲ್ಲಿ ಸಮವಾಗಿರುವ ಬಾಹುಗಳಿಗೆ ಅಭಿಮುಖವಾಗಿರುವ ಕೋನಗಳು ಸಮವಾಗಿರುತ್ತವೆ.

ದತ್ತ: ABC ಯಲ್ಲಿ AC=BC

ಸಾಧನೀಯ:CAB= ABC

ರಚನೆ:  ACB ಯ ಕೋನಾರ್ಧಕ ರೇಖೆಯನ್ನೆಳೆಯಿರಿ. ಅದು AB ಯನ್ನುD ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸಲಿ.

 

ಸಂ.

ನಿರೂಪಣೆ

ಕಾರಣಗಳು

1

AC=BC

ದತ್ತ

2

ACD=DCB

CD ಯು ACB ಯ ಕೋನಾರ್ಧಕ ರೇಖೆ.

3

CD ಸಾಮಾನ್ಯ ಬಾಹು

ACD ಮತ್ತು DCB ಗಳಿಗೆ

4

ತ್ರಿಕೋನ ACD DCB

ಬಾ.ಕೋ.ಬಾ. ಸ್ವಯಂಸಿದ್ಧ

5

CAB= ABC

ಸರ್ವಸಮ ತ್ರಿಕೋನಗಳ ಅನುರೂಪ ಕೋನಗಳು.

 

6.4.3 ಸಮಸ್ಯೆ 3: ಪಕ್ಕದ ಚಿತ್ರದಲ್ಲಿ AB=AC. AL=AM ಆಗುವಂತೆ L ಮತ್ತು M ಗಳು AB ಮತ್ತು AC ಯ ಮೇಲಿನ ಬಿಂದುಗಳು.

 ALM =AML ಅಲ್ಲದೆ,ABM ACL  ಮತ್ತು LCB MBC, LM||BC ಎಂದು ಸಾಧಿಸಿ.

 

ಪರಿಹಾರ:

ಸಂ.

ನಿರೂಪಣೆ

ಕಾರಣಗಳು

1

AL=AM

ದತ್ತ

2

BL = CM

AB=AC, ಹಂತ: 1

3

ALM =LMA

ALMನಲ್ಲಿAL=AM ಆದ್ದರಿಂದ ಪಾದಕೋನಗಳು ಸರ್ವಸಮ (ಪ್ರಮೇಯದಿಂದ)

4

AB=AC

ದತ್ತ      

5

BAM ಸಾಮಾನ್ಯ ಕೋನ

ABM , ACL ಗಳಿಗೆ

6

ABM  ACL

ಬಾ.ಕೋ.ಬಾ. ಸ್ವಯಂಸಿದ್ಧ (ಹಂತ:: 1,5,4)

7

ABC =BCA

ಪಾದಕೋನ ಪ್ರಮೇಯ (AB=AC)

8

LB=CM

ಹಂತ 1,2,3

9

BC ಸಾಮಾನ್ಯ ಬಾಹು

LCB, MBC ಗಳಿಗೆ

10

LCB MBC

(ಹಂತ 2, 7, 9) ಬಾ.ಕೋ.ಬಾ. ಸ್ವಯಂಸಿದ್ಧ           

11

2ALM = 1800-LAM

ALM+LMA+LAM = 1800  , ALM = LMA

12

2ABC = 1800-LAM

ABC+BCA+LAM = 1800  , ABC = BCA

13

ALM = ABC

ಹಂತ 11 ಮತ್ತು 12 ರಿಂದ ಬಲಭಾಗ ಎರಡೂ ಕಡೆ ಸಮವಾಗಿದೆ.

14

LM ||BC

ಅನುರೂಪ ಕೋನಗಳು ಪರಸ್ಪರ ಸಮ(ಹಂತ 13)

 

ಚಟುವಟಿಕೆ: ಅನುಕೂಲವಾದ ಯಾವುದೇ ಅಳತೆಯ ಪಾದದ ಮೇಲೆ ಪಾದಕೋನಗಳು ಸಮವಾಗಿರುವ (300 ಮತ್ತು 300 ಆಗಿರಲಿ) ಎರಡು ತ್ರಿಕೋನಗಳನ್ನು ರಚಿಸಿರಿ.

ನೀವೇನನ್ನು ಗಮನಿಸುವಿರಿ? ಸಮನಾದ ಕೋನಗಳಿಗೆ ಅಭಿಮುಖವಾಗಿರುವ ಬಾಹುಗಳು ಸರ್ವಸಮವಾಗಿರುತ್ತವೆ.

 

6.4.3 ಪಾದಕೋನ ಪ್ರಮೇಯದ ವಿಲೋಮ: ಯಾವುದೇ ತ್ರಿಕೋನದಲ್ಲಿ ಸಮವಾಗಿರುವ ಕೋನಗಳಿಗೆ ಅಭಿಮುಖವಾಗಿರುವ ಬಾಹುಗಳು ಸರ್ವಸಮವಾಗಿರುತ್ತವೆ.

ದತ್ತ: ABCಯಲ್ಲಿCAB= ABC

ಸಾಧನೀಯ: AC=BC

ರಚನೆ: ACB ಯನ್ನು ಅರ್ಧಿಸಿ. ಈ ಕೋನಾರ್ಧಕ ರೇಖೆಯು ABಯನ್ನುD ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸಿದೆ.

ಸಂ.

ನಿರೂಪಣೆ

ಕಾರಣಗಳು

1

CAB= ABC

ದತ್ತ

2

CD ಸಾಮಾನ್ಯ ಬಾಹು

ACD ಮತ್ತು  DCB ಗಳಿಗೆ

3

ACD =DCB

ರಚನೆ

4

ACD  DCB

ಕೋ.ಬಾ.ಕೋ. ಸ್ವಯಂಸಿದ್ಧ

5

AC=BC

 ಸರ್ವಸಮ ತ್ರಿಕೋನಗಳ ಅನುರೂಪ ಬಾಹುಗಳು

 

 

6.4.3 ಸಮಸ್ಯೆ 4: ಒಂದು ಸಮದ್ವಿಬಾಹು ತ್ರಿಭುಜದಲ್ಲಿ ಶೃಂಗಕೋನವನ್ನು ಅರ್ಧಿಸುವ ರೇಖೆಯು ಪಾದವನ್ನು ಅರ್ಧಿಸುತ್ತದೆ ಮತ್ತು ಪಾದಕ್ಕೆ ಲಂಬವಾಗಿರುತ್ತದೆ ಎಂದು ಸಾಧಿಸಿ.

 

ಪರಿಹಾರ:

ದತ್ತ:ABC ಯಲ್ಲಿ AC=BC

ಸಾಧನೀಯ:: AD=DB ಮತ್ತು ADC =CDB = 900

ರಚನೆ:ACB ಯ ಕೋನಾರ್ಧಕ ರೇಖೆಯನ್ನೆಳೆಯಿರಿ. ಆ ರೇಖೆಯು ABಯನ್ನುD ಯಲ್ಲಿ ಸಂಧಿಸಲಿ.

ಸಂ.

ನಿರೂಪಣೆ

ಕಾರಣಗಳು

1

AC=BC

ದತ್ತ      

2

CAB = ABC

ರಚನೆ

3

CDಯು ಸಾಮಾನ್ಯ ಬಾಹು

ACD ಮತ್ತು DCB ಗಳಿಗೆ

4

ACD  DCB

ಬಾ.ಕೋ.ಬಾ. ಸ್ವಯಂಸಿದ್ಧ

5

AD=DB

ಸರ್ವಸಮ ತ್ರಿಕೋನಗಳ ಅನುರೂಪ ಬಾಹುಗಳು

6

ADC = CDB

ಸರ್ವಸಮ ತ್ರಿಕೋನಗಳ ಅನುರೂಪ ಕೋನಗಳು        

7

ADC+CDB=1800

ಸರಳಯುಗ್ಮ ಕೋನಗಳು 

8

ADC =CDB = 900

 

 

ಚಟುವಟಿಕೆ: ಬಾಹುಗಳು 4 ಸೆಂ.ಮಿ., 5 ಸೆಂ.ಮಿ., ಮತ್ತು 6 ಸೆಂ.ಮಿ. ಇರುವಂತೆ ಕೆಲವು ತ್ರಿಭುಜಗಳನ್ನು ರಚಿಸಿ. ನೀವೇನನ್ನು ಗಮನಿಸುತ್ತೀರಿ? ಇವೆಲ್ಲವೂ ಸರ್ವಸಮವಾಗಿರುತ್ತವೆ. ತ್ರಿಕೋನದ ಮೂರು ಬಾಹುಗಳನ್ನು ಕೊಟ್ಟಾಗ ತ್ರಿಭುಜವನ್ನು ರಚಿಸಬಹುದೆಂದು ನಮಗೆ ಗೊತ್ತಿದೆ. 

ಆದ್ದರಿಂದ, “ಒಂದು ತ್ರಿಕೋನದ ಮೂರು ಬಾಹುಗಳು ಇನ್ನೊಂದು ತ್ರಿಕೋನದ ಮೂರು ಅನುರೂಪ ಬಾಹುಗಳು ಸಮವಾಗಿದ್ದರೆ, ಆ ಎರಡು ತ್ರಿಕೋನಗಳು ಸರ್ವಸಮ”. ಈ ಹೇಳಿಕೆಯನ್ನ ತ್ರಿಕೋನಗಳ ಸರ್ವಸಮತೆಯ ಬಾ.ಬಾ.ಬಾ. (ಬಾಹು, ಬಾಹು, ಬಾಹು) ಸ್ವಯಂಸಿದ್ಧ ಎನ್ನುವರು 

6.4.3 ಸಮಸ್ಯೆ 5:  PQRS ಒಂದು ವರ್ಗ. A, B, C, D ಗಳು ಕ್ರಮವಾಗಿ PQ, QR, RS ಮತ್ತು SP ಗಳ ಮಧ್ಯ ಬಿಂದುಗಳು.  BAC=BCA ಎಂದು ಸಾಧಿಸಿ.

 

ಪರಿಹಾರ:

PQ=SR ಒಂದು ವರ್ಗ. ಆದ್ದರಿಂದ PQ = SR. A ಮತ್ತು C ಗಳು PQ ಮತ್ತು SR ಗಳ ಮಧ್ಯ ಬಿಂದುಗಳು.

 AQ=CR.

Bಯು QR ನ ಮಧ್ಯ ಬಿಂದು  QB=BR.

PQRS ಒಂದು ವರ್ಗ   AQB=900 =BRC

AQB  CRB ಬಾ.ಕೋ.ಬಾ ಸ್ವಯಂಸಿದ್ಧ.

AB=BC ……. ಸರ್ವಸಮ ತ್ರಿಕೋನದ ಅನುರೂಪಬಾಹುಗಳು.

CBA ಒಂದು ಸಮದ್ವಿಬಾಹು ತ್ರಿಕೋನ.

ಪ್ರಮೇಯದಂತೆ, ಸಮನಾದ ಬಾಹುಗಳಿಗೆ ಅಭಿಮುಖವಾಗಿರುವ ಕೋನಗಳು ಸಮ. BAC=BCA

 

ಚಟುವಟಿಕೆ: ಒಂದು ತ್ರಿಕೋನದ 2 ಕೋನಗಳು ಮತ್ತು ಸಾಮಾನ್ಯಬಾಹುವು (600,700 ,4 ಸೆಂ.ಮಿ. ಆಗಿರಲಿ) ಇನ್ನೊಂದು ತ್ರಿಕೋನದ 2 ಕೋನಗಳು ಮತ್ತು ಸಾಮಾನ್ಯ ಬಾಹುವಿಗೆ ಸಮವಾಗಿ ಇರುವಂತೆ ಕೆಲವು ಜೊತೆ ತ್ರಿಕೋನಗಳನ್ನು ರಚಿಸಿ. ನೀವೇನನ್ನ ಗಮನಿಸುವಿರಿ? ಪ್ರತೀ ಜೊತೆಯಲ್ಲಿರುವ ತ್ರಿಕೋನಗಳು ಸರ್ವಸಮವಾಗಿರುತ್ತವೆ.

 

           ಯಾವುದೇ ಕೋನಗಳು ಮತ್ತು ಸಾಮಾನ್ಯ ಬಾಹುವನ್ನು ಕೊಟ್ಟಾಗ ಏಕೈಕ ತ್ರಿಕೋನವನ್ನು ರಚಿಸಬಹುದೆಂದು ನಮಗೆ ಗೊತ್ತು. ಹಾಗಾದರೆ ನಾವು ಹೀಗೆ ತೀರ್ಮಾನಿಸಬಹುದು:

“ಒಂದು ತ್ರಿಕೋನದ 2 ಕೋನಗಳು ಮತ್ತು ಒಂದು ಸಾಮಾನ್ಯ ಬಾಹುವು ಇನ್ನೊಂದು ತ್ರಿಕೋನದ ಅನುರೂಪಕೋನಗಳು ಮತ್ತು ಅನುರೂಪ ಬಾಹುವಿಗೆ ಸಮವಾಗಿದ್ದರೆ, ಆ ಎರಡು ತ್ರಿಕೋನಗಳು ಸರ್ವಸಮವಾಗಿರುತ್ತವೆ”. ಈ ಹೇಳಿಕೆಯನ್ನು ತ್ರಿಕೋನದ ಸರ್ವಸಮತೆಯ ಕೋ.ಬಾ.ಕೋ. (ಕೋನ, ಬಾಹು, ಕೋನ) ಸ್ವಯಂಸಿದ್ಧ ಎನ್ನುವರು 

ಉಪನಿಬಂಧನೆ:- (corollary)

“ಎರಡು ತ್ರಿಭುಜಗಳಲ್ಲಿ, ಒಂದರ ಎರಡು ಕೋನಗಳು ಮತ್ತು ಯಾವುದಾದರೂ ಒಂದು ಬಾಹು ಮತ್ತೊಂದು ಅನುರೂಪವಾದ ಎರಡು ಕೋನಗಳು ಮತ್ತು ಒಂದು ಬಾಹುವಿಗೆ ಸಮವಾಗಿದ್ದರೆ, ಆ ಎರಡು ತ್ರಿಭುಜಗಳು ಸರ್ವಸಮವಾಗಿರುತ್ತವೆ”. ಇದನ್ನು ಕೋನ, ಕೋನ, ಬಾಹು (ಕೋ.ಕೋ.ಬಾ) ನಿಬಂಧನೆ ಎನ್ನುತ್ತೇವೆ.

 

ಮೇಲಿನ ಉಪನಿಬಂಧನೆಯ ಸಾಧನೆ:

1) ತ್ರಿಕೋನದ ಎಲ್ಲಾ ಕೋನಗಳ ಮೊತ್ತ =1800

2)  ಎರಡು ಕೋನಗಳನ್ನು ಕೊಟ್ಟಾಗ 3ನೇ ಕೋನವನ್ನು ಕಂಡುಹಿಡಿಯಬಹುದು (=1800 –2 ಕೋನಗಳ ಮೊತ್ತ)

3) ಮೂರು  ಕೋನಗಳಲ್ಲಿ ಯಾವುದಾದರೂ 2 ಕೋನಗಳು ಸಾಮಾನ್ಯ ಬಾಹುವಿನ ಮೇಲೆಯೇ ಇರುತ್ತದೆ.

 

ಆಗ ಎರಡು ತ್ರಿಕೋನಗಳಲ್ಲಿ ಅನುರೂಪ ಕೋನಗಳು ಮತ್ತು ಸಾಮಾನ್ಯ ಬಾಹುವು ಸಮವಾಗುವುದರಿಂದ ಕೋ.ಬಾ.ಕೋ. ಸ್ವಯಂಸಿದ್ಧದ ರೀತ್ಯಾ ಆ ಎರಡು ತ್ರಿಕೋನಗಳು ಸರ್ವಸಮವಾಗುತ್ತವೆ.

6.4.3 ಸಮಸ್ಯೆ 6: ನದಿಯ ಅಗಲವನ್ನು ಅಳೆಯುವುದು:

 

ಪರಿಹಾರ:

ನದಿಯ ಇನ್ನೊಂದು ದಡದಲ್ಲಿ ಒಂದು ಸ್ಥಿರವಾದ ವಸ್ತು (ಮರ) B ಯನ್ನು ಗುರುತಿಸಿ. ನೀವು ನಿಂತ ಈಚೆ ದಡದಲ್ಲಿ B ಗೆ ಎದುರಾಗಿ  A ಕಂಬವನ್ನು ನಿಲ್ಲಿಸಿ.

Aಯಿಂದ¸ ಸ್ವಲ್ಪ ದೂರದಲ್ಲಿ ದಡದ ಮೇಲೆ ಇನ್ನೊಂದು ಕಂಬ C ಯನ್ನು ನಿಲ್ಲಿಸಿ.

CಯಿಂದAC ಯಷ್ಟೇ ದೂರದಲ್ಲಿ D ಕಂಬವನ್ನು ನಿಲ್ಲಿಸಿ.(Cಯು AD ಯ ಮಧ್ಯಬಿಂದು).

AD ಗೆ ಲಂಬವಾಗಿ, B,C ಮತ್ತು E ಒಂದೇ ಸರಳರೇಖೆಯಲ್ಲಿರುವಂತೆ E ಕಂಬವನ್ನು ನಿಲ್ಲಿಸಿ. ಆಗ

1) BAC = 900= CDE (BA ಮತ್ತು DE AD ಗೆ ಲಂಬವಾಗಿ ರಚಿಸಲ್ಪಟ್ಟವುಗಳು).

2) AC=CD (ರಚನೆ)

3) ACB = DCE  (ಶೃಂಗಾಭಿಮುಖ ಕೋನ)

ABC  DEC ಕೋ.ಬಾ.ಕೊ. ಸ್ವಯಂಸಿದ್ಧ    AB=DE 

DE ಯ ಉದ್ದವನ್ನು ಅಳೆಯುವುದರಿಂದ, ನೀರಿಗಿಳಿಯದೇ ನದಿಯ ಅಗಲವನ್ನು ತಿಳಿಯಬಹುದು.

 

6.4.3 ಸಮಸ್ಯೆ 7: ಪಕ್ಕದ ಚಿತ್ರದಲ್ಲಿ ACಯು DF ನ್ನ ಅರ್ಧಿಸುತ್ತದೆ. ಮತ್ತು  EDC =AFE ಆದರೆ AE=EC  ಎಂದು ಸಾಧಿಸಿ.

 

ಪರಿಹಾರ:

ಚಿತ್ರದಲ್ಲಿ AEF =DEC (ಶೃಂಗಾಭಿಮುಖ ಕೋನ)

 

DE=EF, EDC =AFE (ದತ್ತಾಂಶಗಳು)

 

AEF  DEC ಕೋ.ಬಾ.ಕೊ. ಸ್ವಯಂಸಿದ್ಧ

 

AE=EC ಸರ್ವಸಮ ತ್ರಿಕೋನಗಳ ಅನುರೂಪಬಾಹುಗಳು

 

ತಃಖ್ತೆ: ತ್ರಿಕೋನಗಳ ಸರ್ವಸಮತೆಯ ಸ್ವಯಂಸಿದ್ಧಗಳು

ಬಾಹು

ಬಾಹು

ಬಾಹು

ಕೋನ

ಕೋನ

ಕೋನ

ಸ್ವಯಂಸಿದ್ಧ

Y

Y

Y

-

-

-

ಬಾ.ಬಾ.ಬಾ.

Y

-

-

Y

Y

-

ಕೋ.ಬಾ.ಕೋ.

Y

Y

-

Y

-

-

ಬಾ.ಕೋ.ಬಾ.

 

ಗಮನಿಸಿ: ಮೇಲಿನ ತಃಖ್ತೆ ಗಮನಿಸಿ. ತ್ರಿಕೋನಗಳು ಸರ್ವಸಮ ಆಗಲು ಕನಿಷ್ಟ ಒಂದು ಬಾಹುವಾದರೂ ಸಮವಾಗಿರಬೇಕು.

.

6.4.3 ಅಭ್ಯಾಸ: ಮೇಲಿನ ಸ್ವಯಂಸಿದ್ಧಗಳನ್ನು ಉಪಯೋಗಿಸಿ, ಈ ಕೆಳಗಿನ ರಚನೆಯ ಕ್ರಮಗಳು (ಅಧ್ಯಾಯ 6.1 ನೋಡಿ: ಅಲ್ಲಿ ರಚಿಸುವುದನ್ನು ಮಾತ್ರ ಕಲಿತಿದ್ದೆವು) ಸರಿಯೆಂದು ಸಾಧಿಸಿ:

1.      ಕೋನಾರ್ಧಕ ರೇಖೆಯನ್ನೆಳೆಯುವುದು.

2.      ಒಂದು ಸರಳರೇಖೆಯ ಮೇಲಿನ ಬಿಂದುವಿನಲ್ಲಿ ಲಂಬವನ್ನೆಳೆಯುವುದು.

3.      ದತ್ತ ಸರಳರೇಖೆಯ ಲಂಬ ದ್ವಿಭಾಜಕವನ್ನೆಳೆಯುವುದು 

6.4.3 ಪ್ರಮೇಯ: ಎರಡು ಲಂಬಕೋನ ತ್ರಿಭುಜಗಳಲ್ಲಿ ಒಂದರ ಕರ್ಣ ಮತ್ತು ಒಂದು ಬಾಹು, ಮತ್ತೊಂದರ ಕರ್ಣ ಮತ್ತು ಅನುರೂಪವಾದ ಒಂದು ಬಾಹುವಿಗೆ ಸಮವಾಗಿದ್ದರೆ, ಆ ಎರಡು ಲಂಬಕೋನ ತ್ರಿಭುಜಗಳು ಸರ್ವಸಮವಾಗಿರುತ್ತವೆ.

ದತ್ತ:  ABC ಮತ್ತು DEF ಗಳು ಎರಡು ಲಂಬಕೋನ ತ್ರಿಕೋನಗಳು

(ABC =DEF= 900)

AB=DE, AC=DF

ಸಾಧನೀಯ: ABC  DEF

ರಚನೆ: FEಯನ್ನುGE=BC ಆಗುವಂತೆ G ವರೆಗೆ ವೃದ್ಧಿಸಿದೆ. DG ಯನ್ನು ಸೇರಿಸಿದೆ.

 

ಸಂ.

ನಿರೂಪಣೆ

ಕಾರಣಗಳು

 

 

 

 

 

1

AB=DE

ದತ್ತ

2

ABC =DEF= 900

ದತ್ತ

3

ABC =DEG = 900

DEG+DEF = 1800

4

BC=GE

ರಚನೆ

5

ABC DEG

ಹಂತ 1, 3, 4 ರಿಂದ, ಬಾ.ಕೋ.ಬಾ. ಸ್ವಯಂಸಿದ್ಧ

6

ACB=DGE

ಸರ್ವಸಮ ತ್ರಿಕೋನಗಳ ಅನುರೂಪ ಕೋನಗಳು

7

DG=AC

ಅನುರೂಪ ಬಾಹುಗಳು

8

AC=DF

ದತ್ತ

9

DG=DF

ಹಂತ 7, 8

10

DE  ಯು ಸಾಮಾನ್ಯ ಬಾಹು.

DEF   ಮತ್ತು  DEG ಗಳಿಗೆ

11

DEG = DEF = 900

ರಚನೆ

12

DFE = DGE

GDFಗೆ ಪಾದ-ಕೋನ ಪ್ರಮೇಯ

13

GDE = EDF

GDE =1800 –DEG-DGE

=1800 –DEF -DFE= EDF

13

DEG DEF

ಕೋ.ಬಾ.ಕೋ. ಸ್ವಯಂಸಿದ್ಧ  (ಹಂತ 13, 10, 11)

14

ABC DEF

ಹಂತ  5,13

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ಇದನ್ನು ಲಂ.ಕ.ಬಾ. (ಲಂಬ ಕೋನ, ಕರ್ಣ, ಬಾಹು) ಸ್ವಯಂಸಿದ್ಧ ಎಂತಲೂ ಕರೆಯುತ್ತೇವೆ.

 

6.4.3 ಸಮಸ್ಯೆ 8: ಒಂದು ತ್ರಿಕೋನದಲ್ಲಿ ಮೂರು ಎತ್ತರಗಳು ಸಮವಾಗಿದ್ದರೆ. ಅದು ಒಂದು ಸಮಬಾಹು ತ್ರಿಕೋನ ಎಂದು ಸಾಧಿಸಿ.

 

ಪರಿಹಾರ:

ತ್ರಿಕೋನದ ಶೃಂಗ ಬಿಂದುವಿನಿಂದ ಅಭಿಮುಖ ಬಾಹುವಿಗೆ ಎಳೆದ ಲಂಬಗಳೇ ತ್ರಿಕೋನದ ಎತ್ತರಗಳು.

ಪಕ್ಕದ ಚಿತ್ರದಲ್ಲಿ EC,BF ಮತ್ತು AD ಗಳು ಎತ್ತರಗಳು.

ಸಂ.

ನಿರೂಪಣೆ

ಕಾರಣಗಳು

 

 

 

 

 

1

 BEC ಮತ್ತು BFC ಗಳಲ್ಲಿ

2

EC=BF

ಎತ್ತರಗಳು ಪರಸ್ಪರ ಸಮ (ದತ್ತ)    

3

 BEC=BFC = 900

BE ಮತ್ತು BF ಗಳು ಲಂಬಗಳು     

4

BC ಸಾಮಾನ್ಯಬಾಹು

 

5

BEC BFC

ಲಂ.ಕ.ಬಾ.ಸ್ವಯಂಸಿದ್ಧ    

6

ABC = BCA

ಅನುರುಪ ಕೋನಗಳು

7

ADB  ಮತ್ತು ADC ಗಳಲ್ಲಿ

8

 ADB=ADC = 900

AD ಯು ಎತ್ತರ   

9

AD ಸಾಮಾನ್ಯಬಾಹು

 

10

ABC = BCA

ಹಂತ  6 ರಿಂದ

11

ADB ADC

ಕೋ.ಬಾ.ಕೋ. ಸ್ವಯಂಸಿದ್ಧ

12

AB =AC

ಅನುರೂಪ ಬಾಹುಗಳು

13

BC= AC

ಮೇಲಿನಂತೆಯೇ BFC BFA ಎಂದು ಸಾಧಿಸಬಹುದು.

14

AB=AC=BC

ಹಂತ 12,13 ರಿಂದ

 

 

 

6.4 ಕಲಿತ  ಸಾರಾಂಶ

 

 

ಸಂ.

ಕಲಿತ ಮುಖ್ಯಾಂಶಗಳು

1

ಯಾವುದೇ ತ್ರಿಕೋನದಲ್ಲಿ ಮೂರು ಕೋನಗಳ ಮೊತ್ತ 1800

2

ತ್ರಿಕೋನದ ಒಂದು ಬಾಹುವನ್ನು ವೃದ್ಧಿಸಿದಾಗ ಉಂಟಾಗುವ ಬಹಿರ್‍ಕೋನವು ಅಂತರಾಭಿಮುಖ ಕೋನಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮ.

3

ಎರಡು ತ್ರಿಕೋನಗಳಲ್ಲಿ ಅವುಗಳ ಅನುರೂಪ 3 ಬಾಹುಗಳು ಮತ್ತು 3 ಕೋನಗಳು ಸಮವಾಗಿದ್ದರೆ, ಅವು ಸರ್ವಸಮ ತ್ರಿಕೋನಗಳು

4

ಬಾ.ಕೋ.ಬಾ. ಸ್ವಯಂಸಿದ್ಧ

5

ತ್ರಿಭುಜದಲ್ಲಿ ಸಮವಾದ ಬಾಹುಗಳಿಗೆ ಅಭಿಮುಖವಾಗಿರುವ ಕೋನಗಳು ಪರಸ್ಪರ ಸಮ (ಪಾದ-ಕೋನ ಪ್ರಮೇಯ) ಮತ್ತು ಇದರ ವಿಲೋಮವೂ ಸತ್ಯ

6

ಬಾ.ಬಾ.ಬಾ. ಸ್ವಯಂಸಿದ್ಧ

7

ಕೋ.ಬಾ.ಕೋ. ಸ್ವಯಂಸಿದ್ಧ