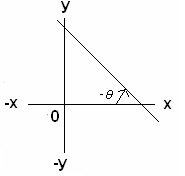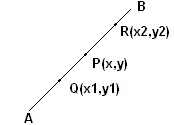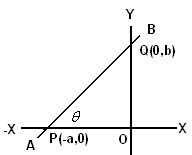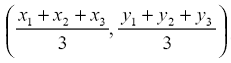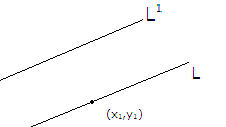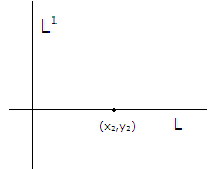7.3 Equation of a line:

Introduction:

In section 7.1 we had studied that the linear equation of the generic form y=mx+c is a straight line. We have learnt that every straight line can be represented as a linear equation. We have also observed that any point on the line satisfies the linear equation and conversely, any point which satisfies the linear equation lies on that line

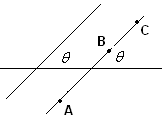
The ‘inclination’ of a line is the angle which the line makes with x axis.


Figure 1	Figure 2	Figure 3
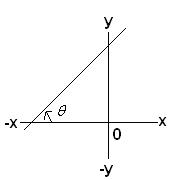
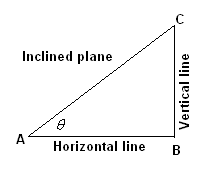
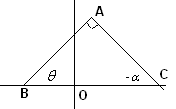
If inclination angle is measured in anti clockwise direction as in Figure 1, is positive	If inclination angle is measured in clockwise direction as in Figure 2, is negative.	The ‘slope’ of any inclined plane (see Figure 3) is the ratio between the length of vertical line to the horizontal line
If is the angle made by the inclined plane to the horizontal line, then Slope = Length of Vertical line/Length of horizontal line = BC/AB=tan (Refer section 8.1) The ‘slope’ of a straight line is the tangent (tan) of inclination and is denoted by letter m. m=tan

Observations:

1. Slope of x axis = 0 (tan=0 as =0⁰)

2. Slope of y axis = undefined (tan= as =90⁰)

3. Slope of a line is positive (tan), if it makes an acute angle in the anti-clockwise direction with x–axis (Figure 1)

4. Slope of a line is negative (- tan= tan(-), if it makes an obtuse angle in the anti-clockwise direction with x–axis or an acute angle in the clockwise direction with x–axis (Figure 2)

Slope of a straight line passing through fixed points

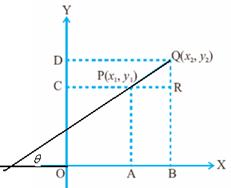
Let P (x₁,y₁) and Q (x₂,y₂) be the two given points.

We are required to find the slope of the line PQ.

Extend QP to meet x-axis to form the angle with x-axis

Since CR is || x-axis

= QPR

m = tan = QR/PR = (y₂- y₁)/ (x₂- x₁) = (y₁- y₂)/ (x₁- x₂)

1. Note that slope of two parallel lines are same.

(Parallel lines make same inclination with x-axis)

Conversely, if the slopes of two lines are same then they are parallel.

2. From above, it follows that slopes of lines joining points on a straight line are same.

Relationship between slopes of two perpendicular lines:

Let BAAC. Let be the angle of inclination of AB with x axis.

Let - be the angle of inclination of AC with x axis (acute angle measured in clock-wise direction)

Slope of AB = tan = AC/AB

Since slope is negative if the angle of inclination is obtuse in anti-clockwise direction,

Slope of CA = - tan = - (AB/AC) Slope of AB * Slope of CA = (AC/AB)*-(AB/AC) = -1.

3. Thus the product of slopes of two perpendicular lines is -1; conversely, if the product of slopes of two lines is -1 then the lines are mutually perpendicular

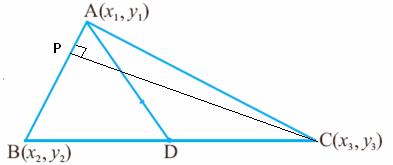
7.3 Problem 1: A(5,4),B(-3,-2) and C(1,-8) are the vertices of a triangle ABC. Find

(I) The slope of altitude of AB,

(II) The slope of the median AD

(III) The slope of the line parallel to AC.

Solution:

(I)

By formula, the slope pf AB = (4-(-2))/(5-(-3)) = (6/8) = 3/4

Since the product of slopes of two perpendicular lines is -1

The slope of CP which is perpendicular to AB = -4/3

(II)

In order to find the slope of AD we need to find the point D(x,y)

Since D is mid point of BC

x= (-3+1)/2 = -1 : y = (-2+(-8))/2 = -5

Thus D is D(-1,-5).

Slope of AD = ( 4-(-5))/(5-(-1)) = 9/6 = 3/2

(III)

Slope of AC = (4-(-8))/(5-1) = 12/4 = 3

Thus any line parallel to AC has same slope of 3

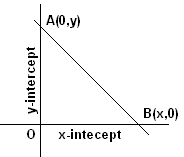
Intercepts:

In section 7.1 we have learnt what intercepts are.

To recollect,

x-intercept is the distance from O to the point where the line cuts x-axis(x co-ordinate).

y-intercept is the distance from O to the point where the line cuts y-axis(y co-ordinate).

Forming equation of a line:

We have studied that y=mx+c is the general format for the equation of a line and we have also studied what slope is.

Let us formulate an equation for a given line.

1. Slope-intercept form

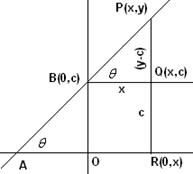
Let P be any point on the given line with co-ordinates (x,y).

Let AB be the line and be it’s angle of inclination.

Let its y-intercept be c, hence OB=c=RQ

PQ = PR-QR = y-c

From the figure it is clear that

PBQ =

m = tan = PQ/BQ = (y-c)/x

mx = y-c

i.e. y = mx+c is the equation of the given line AB.

2. Slope-Point form

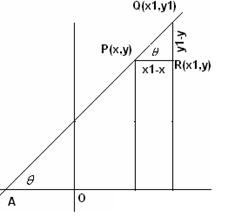
Let AP be the line and be it’s angle of inclination.

Let Q(x₁.y₁) be any point on AP.

From the figure it is clear that R is R(x₁,y)

Hence PR=(x₁-x) and RQ = (y₁-y)

Also

QPR =

m = tan = QR/PR = (y₁-y)/(x₁-x)

m(x₁-x) = (y₁-y) (Multiply both sides by -1 to get)

y-y₁ = m(x-x₁)

Note y = mx+(y₁- mx₁) is the equation of the given line AP which is of the form y=mx+c

3. Two Point form

Let R(x₂,y₂),Q(x₁,y₁) be two points on the given line AB.

We are required to find the equation of this line.

As learnt earlier in this section, the slope of a line through two points is:

Slope of AB = m = (y₂-y₁)/(x₂-x₁). Let P (x,y) be another point on this line

It’s slope = m = (y-y₁)/(x-x₁)

y-y₁ = m(x-x₁)

i.e. y = mx+(y₁-mx₁) where m = (y₂-y₁)/(x₂-x₁) which is of the form y=mx+c. This is the equation of the given line AB passing through 2 points.

4. Intercepts form:

Let P(-a,0) and Q(0,b) be the x and y intercept respectively of the line AB.

m = Slope of AB = tan = OB/OA = b/(-a) = -b/a

From Slope – intercept form which was discussed earlier in this section

The equation of a line AB is y = mx + (y-intercept)

= -(b/a)x+b (Note Y intercept = b)

i.e. y = (-bx+ab)/a

i.e. ay = -bx+ab

i.e. ay+bx = ab

i.e. (y/b) + (x/a) = 1

7.3 Problem 2: A(1,4),B(3,2) and C(7,5) are the vertices of a triangle ABC.

Find

(i) The co-ordinates of the centroid of triangle ABC

(ii) The equation of the line through the centroid of the triangle and parallel to AB

Solution:

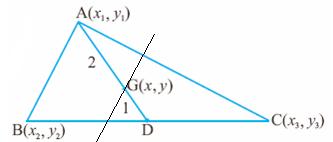
(i) In section 7.2 we have learnt that the co-ordinates of centroid G(x,y) of any triangle is:

x = (1+3+7)/3 =11/3 y = (4+2+5)/3 = 11/3 G(x,y) = G(11/3,11/3)

(ii) Slope of the line passing through G and || to AB, is same as the slope of AB.

Slope of AB = m = (y₂-y₁)/ (x₂-x₁) = (2-4)/(3-1) = -1

The equation of the line passing through G(x,y) and having a slope of -1 is (slope–point form)

y = mx+(y₁-mx₁) Note: Here x₁ and y₁ are co-ordinates of G.

y = -x + [11/3-(-1)(11/3)] = -x+22/3

i.e. 3x+3y = 22 is the equation to the line, parallel to AB and passing through the centroid G of the triangle ABC.

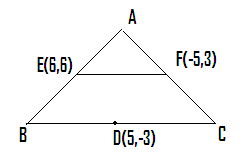
7.3 Problem 3: The mid points of three sides of a triangle are (5,-3), (6,6) and (-5,3).

Find the equation of the sides of the triangle.

Solution:

Let the triangle be ABC and D, E and F be the mid points of BC, AB and AC respectively,

so that the co–ordinates of D, E and F are (5,-3), (6,6) and (-5,3) respectively.

We are required to find the equation to the lines BC, AB and AC.

Hint:

Note that BC||EF and hence the slope of BC = Slope of EF = 3/11

Hence the equation to BC is 3x-11y = 48 (use slope-point form)

DE||AC, Slope of AC = slope of DE = 9 and hence the equation to AC is 9x-y+48=0

DF||AB, Slope of AB = slope of DF = -3/5 and hence the equation to AB is 3x+5y=48

Equation of lines parallel and perpendicular to a given line.

Let L be a line passing through the point (x₁,y₁) with slope m.

Then the equation of L is y = mx+(y₁-mx₁) which is of the form y=mx+c₁ where c₁ = (y₁-mx₁).

Let L¹ be a line parallel to L and passing through the point (x₂,y₂) with slope m_1.

Then the equation of L¹ is y = m₁x+(y₂-m₁x₂)

Since L and L¹ are parallel, m=m_1.

Hence the equation of L¹ is y = mx+(y₂-mx₂) = mx+c₂ ,where c₂= (y₂-mx₂).

1. Thus equations of two parallel lines differ only by constants.

( For L it is mx+(y₁-mx₁) and for L¹ it is mx+(y₂-mx₂))

Let L be a line passing through the point (x₁,y₁) with slope m = tan.

Then the equation of L is y = mx+(y₁-mx₁)

Let L¹ be a line perpendicular to L and passing through the point (x₂,y₂) with slope m₁.

Then the equation of L¹ is y = m₁x+(y₂-m₁x₂)

Earlier in this section, We have learnt that product of slopes of two perpendicular line is -1.

m₁= -1/m

2. Thus the equation of L¹ which is perpendicular to L is y = –(1/m)x+(y₂+(1/m)x₂)

Let ax+by+c = 0 be an equation in first degree.

(i) If a = 0 then y =-c/b which represents a line parallel to x-axis

(ii) If b = 0 then x = -c/a which represents a line parallel to y-axis

(iii) If b is non zero then y = (-a/b)x-(c/b) = mx+c which represents an equation of a straight line.

3. Thus ax+by+c = 0 represents an equation to a straight line.

The general form of an equation to a line is ax+by+c = 0 with a,b,c R. Properties of this line depends on the values of a, b, c and are as follows:

Value of			Equation :	Line :	Slope :	x-intercept:	y-intercept:
a	b	c	Equation :	Line :	Slope :	x-intercept:	y-intercept:
= 0	0	= 0	y=0	x-axis	0	-	0
= 0	0	0	y=-c/b	\|\|to x-axis	0	-	-c/b
0	0	= 0	y=-(a/b)x	Line through O(0,0)	-(a/b)	0	0
	0	0	ax+by+c=0	Neither \|\| to x-axis nor \|\| to y-axis	-(a/b)	-(c/a)	-(c/b)
	= 0	0	x=-c/a	\|\| y-axis		-(c/a)	-
	= 0	= 0	x=0	y-axis		0	-

7.3 Problem 4: Find the equation of a line passing through (4,-3) and perpendicular to the line 2x-5y+4=0

Solution:

Slope of the given line 2x-5y+4=0 is 2/5 (y = (2/5)x+(4/5))

Slope of the line perpendicular to the above line is –(5/2) (the product of the slopes of two perpendicular lines =-1)

Since this perpendicular line passes through (4,-3) its equation is

y= mx+(y₁-mx₁) = –(5/2)x + (-3) + (5/2)4

= –(5/2)x+ 7

i.e. 2y = -5x+14 Or 5x+2y-14=0

Testing concurrency of straight lines when their equations are given:

Steps:

1. Solve any two equations to get their point of intersection

2. Substitute the co-ordinates obtained from step 1 in the third equation

3. If the third equation is satisfied then the point is on the third line and hence the three lines are concurrent

7.3 Summary of learning

No	Points to remember
1	If P (x₁,y₁) and Q (x₂,y₂) then m = (y₁- y₂)/(x₁- x₂)
2	If m is the slope and c is the y-intercept then y = mx+c
3	If m is the slope and P (x₁,y₁) is a point on this line then y = mx+(y₁-mx₁)
4	If P (x₁,y₁) and Q (x₂,y₂) are two points then y = mx+(y₁-mx₁) where m = (y₂-y₁)/(x₂-x₁)

Their Name:
Their Email:
Your Email:
Your Name:
Your message to your friend: