7.5 Graphical method of solving a Quadratic equations:

We have learnt how to draw graph for an equation of type y=mx+c(Where m is a constant).

We have also observed that the equation of this type represents a straight line.

Let us learn to solve quadratic equation of type ax² +bx+ c =0

We can solve the equation by two methods

First method:

ax² +bx+ c = 0 can be written as

ax²= -bx-c

Let each be equal to y

So we have two equations y = ax²and y =-bx-c

Draw the graph for both these equations. The intersecting points of the two graphs are solutions to the given equation ax² +bx+ c=0

Note that y = =bx-c is an equation to a line. Problem 7.5.1 illustrates this method.

Second method:

Draw the graph ax² +bx+ c and then find the points on the graph which touches x-axis (I.e. when y=0).The x-co-ordinates of the points on the graph, whose y-co-ordinates are zero, are roots of the given equation. Problem 7.5.2 illustrates this method.

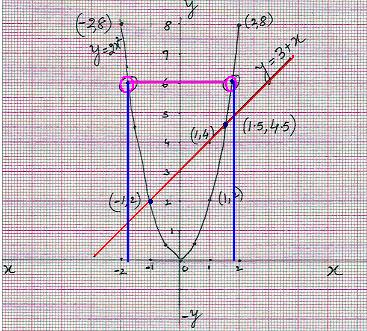
7.5 Problem 1: Draw the graph for y=2x² and y= 3+x and hence

1. Solve the equation 2x²-x-3=0

2. Find the value of

Solution:

1. Solving of equation 2x²-x-3=0

Step 1: For few values of x tabulate the values of y (=2x²) as shown below:

x à	0	1	-1	2	-2
y à	0	2	2	8	8
(x, y)	(0,0)	(1,2)	(-1,2)	(2,8)	(-2,8)

Step 2: On a graph sheet mark the (x, y) co-ordinates. Join these points by a smooth curve. This smooth curve is called ‘parabola’

Step 3: For two values of x tabulate the values of y (=3+x) as shown below

x à	-1	1
y à	2	4
(x, y)	(-1,2)	(1,4)

Why did we ask you to find coordinates for only 2 values of x?

(y=3+x is of type y=mx+c and it represents a straight line. To draw a straight line, two points are enough)

Step 4: On a graph sheet mark these two (x,y) co-ordinates. Join these two points.

The parabola and the straight line cut each other at two points. They are (-1, 2) and (1.5, 4.5).

Their x co-ordinates are -1 and 1.5 respectively.

-1 and 3/2 satisfy the given equation 2x²-x-3=0.

Verification:

The given equation 2x²-x-3=0 is of the form ax² +bx+ c =0. We have learnt that the roots of this equation are x = [-b (b²-4ac)]/2a Here a=2, b= -1,c= -3 (b²-4ac) = (1+24)= 5

The roots are (15)/4 = -1 and 3/2 which are as derived using the graphical method

2. Finding value of :

We need to find the value of y when x =. The graph for parabola is of the form y=2x². Thus if x = then y=2x²= 6 So we need to find the value of x when y=6. From the graph we can see that there are two values of x (circled points in the graph in I Quadrant and II Quadrant) which satisfy y=6

We notice that x co-ordinate of the parabola at y=6 are -1.7 and +1.7 which gives the value of

Exercise and observations:

1. Draw few graphs for the equation y =mx² for few values of m (both +ve and –ve) and observe the following:

- All graphs are parabolas and pass through the origin

- They are all symmetric about y-axis.

2. Draw few graphs for the equation x =my² for few values of m (both +ve and –ve) and observe the following:

- All graphs are parabolas and pass through the origin

- They are all symmetric about x- axis.

7.5 Problem 2: Solve the equation 2x²+3x-5=0

Solution:

Step 1: For few values of x tabulate the values of y(=2x²+3x-5) as given below:

x à	0	1	-1	2	-2	-3
y à	-5	0	-6	9	-3	4
(x, y)	(0,-5)	(1,0)	(-1,-6)	(2,9)	(-2,-3)	(-3,4)

Step 2: On a graph sheet mark these (x, y) co-ordinates.

Join these points by a smooth curve. This smooth curve is a parabola.

We need to find the point on graph when 2x²+3x-5=0( i,e when y=0)

We notice that the graph touches the x axis (note that y=0 for any point on x axis) at

x= -2.5(= -5/2) and at x=1.

Therefore 1 and -5/2 are the roots of the given equation.

Verification: The given equation 2x²+3x-5=0 is of the form ax² +bx+ c =0

We have learnt that the roots of this equation are

x = [-b (b²-4ac)]/2a Here a=2, b= 3,c= -5

Determinant b²-4ac = 9+40=49 (b²-4ac) = 7

The roots are (-37)/4

I.e. = 1 and -5/2 are the roots which we derived using the graphical method

Exercise and observations:

Draw graphs for the following equations in both the methods and observe the following

	Equation	Method1		Method 2		Reason
		Draw 2 graphs	Observations	Draw 1 graph for	Observations	Determinant = b²-4ac =
1	2x²+2x-15=0	y = 2x² y = -2x+15	The graphs meet at two points:(-5,0),(3,0)	2x²+2x-15	The graph touches x axis at 2 points and thus has two roots.	4-60=64 = 8² (perfect square)
2	4x²-4x+1=0	y = 4x² y = 4x-1	The graphs meet at one point: (1/2,0)	4x²-4x+1=0	The graph touches x axis at 1 point and has only one root	16-16=0 (zero)
3	x²-6x+10=0	y = x² y = 6x-10	The graphs do not meet at all!	x²-6x+10=0	The graph does not touch x axis and thus no roots.	36-40 = -4 (negative)

7.5 Summary of learning

No	Points studied
1	Quadratic equations can be solved by drawing graphs

Their Name:
Their Email:
Your Email:
Your Name:
Your message to your friend: