6.1 Introduction:
Geometry is that branch of mathematics which studies the
properties of figures such us lines, triangles, quadrilaterals etc.
Ancient Indians used the geometrical properties for
construction of fire places called ‘yajnakundas’. They also had profound knowledge of
astronomy, as even today the method of
calculation of occurrences of eclipses are precise and date and times are arrived at
many years in advance of their
occurrence.
1.
Can
you divide the below mentioned line segment in to two exact parts without using
the scale?

2.
What
should be the size of underground tank to store petrol/milk and water supplied
through tankers?
3.
Why
do people who prepare sweets, makers cut the ‘burfi’
in the shape of parallelograms rather than rectangulars?
In geometry we find answers/solutions to above mentioned concepts/problems.
6.1.0
Definitions and some basic constructions:
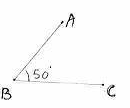
Definition:
|
‘Angle’ is
a figure formed by two rays with a common end point. They are measured in
degrees (00 to 3600) The
common end point is called ‘vertex’. In
the above figure B is a vertex; ABC is an angle and is denoted by |
|
|
No |
Type of angle |
Measure of angle
is |
Example in the
adjacent figure |
|
|
1 |
Acute Angle |
Between 00 and 900 |
|
|
|
2 |
Right Angle |
= 900 |
|
|
|
3 |
Obtuse Angle |
Between 900 and 1800 |
smaller |
|
|
4 |
Straight Angle |
= 1800( Angle on straight line) |
|
|
|
5 |
Reflex Angle |
Between 1800 and 3600 |
Larger |
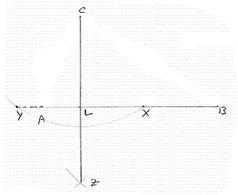
6.1.1. Construction
of Perpendicular to a line from a point.
|
Step 1:
Draw the line AB of given measurement and C be an external point. Step 2: With C as center, draw an arc of suitable radius
to cut the line AB at 2 points (If necessary extend the line) X, Y as shown in the
figure. Step 3: With X and Y as centers, draw arcs (of radius
more than half of XY) to cut at point Z on the other side of AB. Step 4: Join C, Z to intersect the line AB at L CL is perpendicular to AB. Note: The procedure for construction of perpendicular at
a point on the line is same as above. (C could be a point like L on AB) |
|
Note:
Using SSS and SAS postulate (Refer Section 6.4.3), you can prove that ![]() CLY =
CLY =![]() CLX = 900)
CLX = 900)
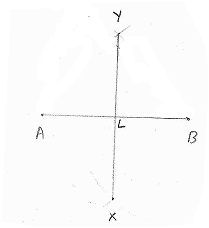
6.1.2. Construction
of Perpendicular bisector to a line.
|
Step1 : Draw the line AB of given measurement. Step2: With A, B as centers, draw
arcs of radius more than half the length of AB on both sides of AB. Let these
arcs meet at X and Y. Step3: Join XY to meet AB at L. (Note that XY bisects AB and XY is perpendicular to AB and
L is mid point of AB) |
|
Note:
Using SSS and then SAS postulate (Refer Section 6.4.3), you can prove
that ![]() ALY =
ALY =![]() YLB = 900)
YLB = 900)
6.1.3. Construction
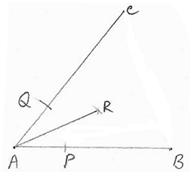
of Angular bisector.
|
Step1: construct Step2: With A as center, draw arcs of same radius to cut
the sides AB and AC at P and Q respectively. Step3: With P and Q as centers as and with more than
half of PQ as radius, draw arcs to intersect at R. Step4: Join |
|
Note:
Using SSS postulate (Refer Section 6.4.3), you can prove that ![]() CAR =
CAR =![]() RAB)
RAB)
|
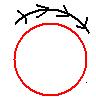
Locus is the path traced by a moving point, which moves so as
to satisfy the given condition/conditions. An example is the circumference
of a circle. Any point on a
circumference is at equal distance from the center of the circle. Thus circumference
is locus of circle. |
|
6.1 Summary of learning
|
No |
Points learnt |
|
1 |
Definitions
and basic constructions |