6.12 Circles - Part 3:

6.12.1: Arcs of a circle

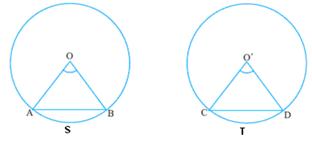
Two arcs of two different circles having same radii are said to be ‘congruent’ if their central angles are same.

Arc ASB = Arc CTD if AOB = CO’D

6.12.1 Theorem 1: If two arcs are congruent then their chords are equal

To prove: AB=CD

Proof:

1. OA = O’C, OB = O’D (Radii)

2. AOB = CO’D (it is given that arcs are congruent)

Hence by SAS Postulate on congruence AOB CO’D

Hence AB = CD

6.12.1 Theorem 2: If two chords of circles having same radii are same,

then their arcs are congruent.

Note: This is converse of the previous theorem.

Use SSS postulate to show that AOB = CO’D

6.12.1: Areas of sectors/segments of circle

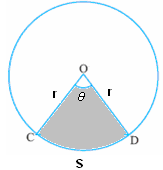
If ‘r’ is the radius of a circle, we know that the circumference and area of the circle are given by

Circumference of the circle = 2r,

Area of the circle = r²,

Where is a constant whose approximate value we use for our calculations is 22/7 (3.1428).

If (where is in degrees) is the angle at center (COD) formed by the arc CSD then

1. Length of the arc CSD = (/180) *r

2. Area of the sector CSDO (shaded portion in the adjoining figure) = (/360) *r²

= (/180) *(r*r)/2 = {(/180) *r}*(r/2)

= Length of the arc*(radius/2)

Note: radians = 180⁰ and x⁰ = (x*)/180 radians

Let AOB = in the adjoining figure with AB as chord

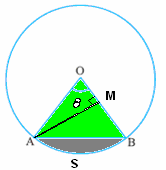
We note that

Area of triangle ABO = (1/2)*base*height = (1/2)*BO*AM = (1/2) *r*rsin= (1/2) r²*sin

(AM = rsin : Refer to section 7.1 for definition of sin of an angle)

From the figure we notice that

Area of Sector ASBO = Area of triangle ABO + Area of segment ASB

Area of segment ASB = Area of Sector ASBO - Area of triangle ABO

= (/360) *r²- (1/2) r²*sin

= r²{(*/360) - (sin/2)}

Note: For all the above calculations must be in degrees.

6.12 Summary of learning

No	Points to remember
1	Congruency of arcs
2	Formula for length of an arc, area of an arc, Area of a segment