4.1
Profit and loss:
1 Assume that
you have a friend who is a merchant who sells chocolate and biscuits in addition to other items
1.
He sells chocolate at 11Rs after buying them at 10Rs
2.
He sells biscuit packet at 23 Rs after buying them at 20Rs
If he wants more
profit from his sales, what do you suggest him to sell more of chocolate or more biscuit packets?
2
A
shop keeper buys 1000 coconuts by paying Rs 6000. Of these 100 coconuts were
spoiled. If he sells remaining coconuts at Rs 5, did he incur loss or profit?
We shall learn to solve these types of problems in this
and subsequent lessons
4.1.1 Percentage:
You must have heard the word percentage very often (%
marks, % rate of interest, %pass in the board examination…)
The word percent can be split as per
and cent and means per 100
Definition: ‘Percentage’ is a fraction with denominator as
100 and is represented by the symbol %.
Examples are :
7% = 7 out of 100 = 7/100 = 0.07
0.025 = 0.025*100% = 2.5%
1/5 = 1/5*100% = 20%
100% means 100 out of 100
4.1.1
Example 1:
Let your marks in mathematics be as given below:
1) In the first monthly test it is 15 out of 25
( 15/25)
2) In the Mid term examination it is 65 out of
100(65/100)
3) In the third monthly test it is 34 out of
50(34/50)
4) In the final examination it is 105 out of 150(
105/150)
With the above data how can we compare your progress in
Mathematics in a year?
You must have thought why not conduct examination for 100
marks always, so that comparison is easy. We can use percentage calculation to
measure the progress.
For calculating % we convert the basis of comparison
(denominator) to 100
Let us convert the basis of comparison to 100 in case of
above example
1. The marks scored in the first test can be represented
as
For 25, the marks is 15
For 100 how much? = (15/25)*100 = 60
Thus the marks got in the first monthly test is 60%
2. Since the mid term exam is based on 100, conversion is
not required and hence marks got is 65%
3. The marks in the third monthly test can be represented
as
For 50, the marks is 34
For 100 how much? = (34/50)*100 = 68
Thus the marks got in the first monthly test is 68%
4. The marks got in the in the final examination can be
represented as
For 150, the marks is 105
For 100 how much? = (105/150)*100 = 35*2 = 70
Thus the marks got in the final examination is 70%
We conclude that marks scored in mathematics are 60%, 65%,
68% and 70%.
4.1.1
Problem 1: An
architect’s fees are worked out at 10% of the first Rs. 25,000 and 4% on the
reminder of cost. If the cost of house is Rs. 1, 50,000 find out
(1) Architect’s fee
(2) Express the architect’s fee as % to the total
cost
Solution
:
The cost of house can be split as25,000 and
1,50,000(1,50,000 = 25000+125000)
Since Architects fee are different for different amount,
we need to be calculate the fee separately on 25,000 and 125000
1. Architect’s fee on 25,000 is 10%
10% on 25,000 = 25000*10/100 = 2500
2. Architect’s fee on 1,25,000 is 4%
4 % on 125000= 125000 *4/100 = 5000
Total fee = 2500+5000 = 7500
For the total cost of house of Rs. 1, 50,000 his fee is Rs
7500
For a cost of Rs 100 the fee is =(7500/150000 )*100
=5
Thus we can say the architect has charged a fee of 5% on
the total cost
Verification:
5% of 150000 = (5/100)* 150000 = 7500, which is the fee
charged by the architect and hence our answer is correct
4.1.1
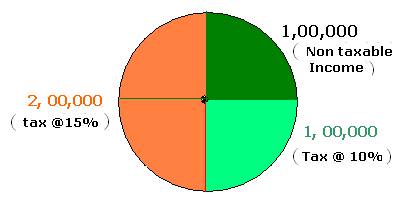
Problem 2:
Government of
|
1) Of
the total income, tax is not collected on the first Rs.1,00,000 2) On
the next 1 Lakh rate of tax is 10% 3) On
the rest of the income tax rate is 15% 4) In
addition, on the total tax collected it charges an educational cess(levy) of
2% Find
out the following for an individual whose income is Rs 4,00,000 (1)
Total tax paid by the individual (2)
Express the total tax as % to the total income |
|
Solution
:
Total income = 4, 00,000
Non taxable income = 1, 00,000
Taxable income = 3, 00,000
Since the tax rates are different for different amount,
this taxable income needs to be split as 1,00,000 and 2,00,000. We also need to
be calculate tax separately on these two amounts.
1) On the first 1 Lakh the tax is at 10%
10% Tax on 1,00,000 = 100000*10/100 =
10,000
2) On the next 2 Lakhs the tax is at 15%
15% Tax on 2,00,000 = 200000*15/100 = 30,000
Thus the total Income tax to be paid is
40,000(10,000+30,000)
In addition to tax am educational cess of 2% has to be
paid
2% cess on 40,000 = = 40000*2/100 = 800
Total tax payable is = I.Tax
+cess = 40000+800 = 40800
On the total income of Rs. 4, 00,000, tax is Rs
40800
On an income of Rs 100 the tax is =
(40800/400000)*100 =10.2%
Thus we can say the tax payable by this individual is
10.2%
Verification:
10.2% of 400000 = (10.2/100)* 400000 = 40800, which is the
total tax to be paid by the individual.
4.1.1
Problem 3: The
population of a town is 24,000. If the number of males is increased by 6% and
that of females by 9%, the population would be 25,620 . Find the number of
females in the town.
Solution
:
|
Let x
be the number of males in the town. Then 24,000-x will be number of
females Since
the increase in males is 6% , the increase in males = x*6/100 Since
the increase in females is 9% , the increase in females =
(24000-x)*9/100 Total
increase =
x*6/100 + (24000-x)*9/100 =6x/100+
240*9 -9x/100 = 2160-3x/100 The
total population = original population + increase = 24,000 + 2160-3x/100 This is
given to be 25,620 25620 =
26160 -3x/100 3x/100
= 26160-25620 (Add 3x/100 to both sides and subtract 25620 from both sides)
Thus
number of males are 18,000 and number of females is 6000 Verification: Since
the increase in males is 6%, the increase in number of males =
18000*6/100 = 1080 Since
the increase in females is 9%, the increase in number of females = 6000*9/100
= 540 Total
increase = 1080+540 = 1620 Thus
the total population = original population + increase = 24,000 + 1620= 25620,
which is as given in the problem. |
|
4.1.1
Problem 4: Divide
the sum of Rs 45,500 among three persons A,B, C in such a way that A gets
(33)1/3% more than B and C gets 60% of A and B together get.
Solution
:
Let x be the amount got B
Since A gets 33 1/3 % more than B the amount got by A
= amount got by B +(33) 1/3 % of B = x+ 33(1/3)x/100 = x+(1/3)x = 4x/3
The amount got by A and B together = 4x/3+x = 7x/3
Since C gets 60% more than what A and B got together,
Amount got by C= 60% of (amount got by A and B together)
= (7x/3)*60/100 = 7x/5
The amount got by A+ amount got by B and amount got by C =
4x/3+x+7x/5
= (20x+15x+21x)/15 (15 is LCM of 3 and 5)
=56x/15
It is given that the total amount distributed is 45,500
45500 = 56x/15
On simplification we get x =
12187.5 which is the amount got by B
Amount got by A = Amount got by B +(33) 1/3 % of
B
= 12187.5 + 33(1/3)% of 12187.5 = 12187.5+ 4062.5 =16250
Amount got By A and B = 16250+12187.5 =28437.5
Amount got by C= 60% of (amount got by A and B
together)
= .6*28437.5 = 17062.5
Verification:
Check the following:
1. 16250 is (33)(1/3)% more than 12187.5
2. 17062.5 is 60% of (12187.5+16250)
4.1.2 Profit and Loss
You must have been to provision stores to buy daily
requirements. The merchant sells items at a price to you after he buys same
from the market or a producer of items.
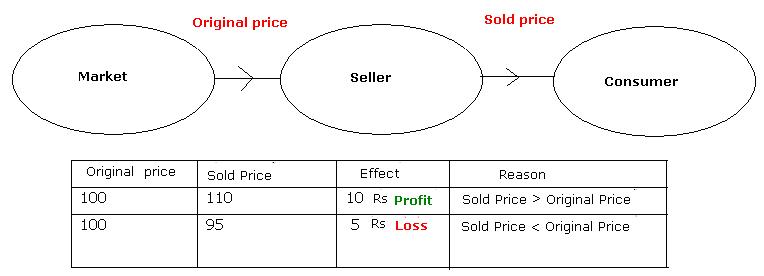
The price at which the item is sold is called ‘selling price(SP)’. In order to sell items to
you, he has to buy these items from some one, may be from a producer or from
another merchant.
The price at which the item is purchased is called ‘Cost price(CP)’
The merchant has his own expenses (He pays rent for the
shop, pays for electricity bills, and pays salary to employees…). For this
reason the seller has to sell items at a price more than the price at which he
has bought the items.
The extra money he gets is difference between selling
price and cost price. It is called profit.
Profit = SP-CP (
SP>CP)
There can be situations where a merchant wants to get rid
of old stock of items. In such cases, he may sell items at a price less than
the purchase price. In such cases he incurs loss.
Loss = CP-SP ( SP<CP)
Though we may buy items in smaller quantities from the
merchant, the merchant always purchases items in large quantities.
Since the merchant buys in large quantities he gets some
reduction in prices from the first (original) supplier.
The price at which goods are bought or sold on a large
scale is called ‘Wholesale price’
The price at which goods are bought or sold on a small
scale is called ‘Retail price’
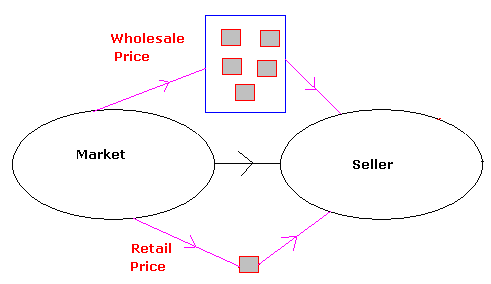
Whole sale price is always < Retail
Price.
Suppose a shop owner is a friend of yours. Apart from
selling other items assume he sells chocolates and biscuits as follows:
1. He sells a bar of chocolate at 11 Rupees which was
purchased by him at 10 Rupees
2. He sells a packet of biscuits at 23 Rupees which was
purchased by him at 20 Rupees
He wants to make more profit. For that, he is not sure
whether he should sell more biscuits or more chocolates. Since you are a student of mathematics he
wants your advice!. What will you suggest to sell more chocolates or more
biscuits?
|
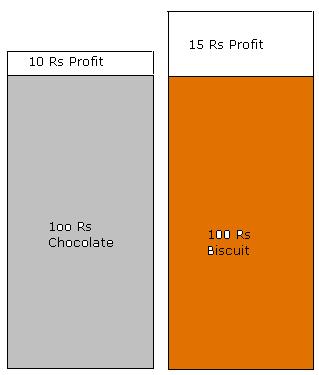
In the
first case for every chocolate of 10Rs, he got
a profit of 1Rs. So, for
chocolates of 100 Rs (=10Chcokolate bars) his
profit was 10Rs(=10*1) In the
second case for every biscuit pack of 20Rs, he got
a profit of 3Rs. So, for
biscuits of 100 Rs (=5 packs) his profit was 15 Rs (=5*3) So, for
same amount of sale (=100 Rs), he gets 5 Rs(=15-10) extra if he sells
biscuit packs. Thus it
is profitable to sell more biscuits than chocolates. |
|
What did we do? In both the case we arrived at his profit
on sale of 100Rs (%) to Cost Price (CP).
The ‘profit percentage’
is the profit made on a Cost price of 100Rs.
There could be losses on sales also
The ‘loss percentage’ is the
loss made on a Cost price of 100Rs.
The formulas used for various calculations are:
Profit = SP-CP
Loss = CP-SP
Profit % = Profit*100/C.P.
Loss % = Loss*100/C.P.
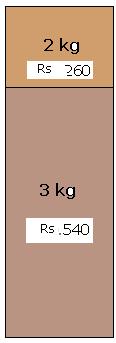
4.1.2 Problem 1: A grocer mixed 3 kg of tea powder at Rs 180Rs
per kg with 2kg of tea powder at Rs.130 per kg. If he sells the mixture of two
at Rs 192 per kg. Did he make profit or loss and what is the percentage?
Solution
:
|
1. Cost
of 3kg tea powder @180 Rs = 3*180*3 = Rs 540 2. Cost
of 2kg tea powder @130 Rs = 2*130*2 = Rs 260 Total
cost of tea powder = Rs
800 By
mixing tea powders he will have total of 5 kg of tea powder. His
sale price of 5kg at Rs 192 = 192*5
= Rs. 960 Since
SP > CP, he has made a profit
|
|
4.1.2 Problem 2: A coconut seller purchased 1000 coconuts for
Rs.6000. Unfortunately 100 coconuts were rotten. He sold remaining coconuts at
Rs each. Find the profit %.
Solution
:
Since 100 coconuts were rotten the seller was left with
only 900 coconuts.
The money he got by
selling 900 coconuts at Rs.5 = 900*5 = 4500
Since SP> CP he has made a loss = CP-SP =6000-4500 =
1500.
Loss % =
Loss*100/C.P.= 1500*100/6000 = 25%
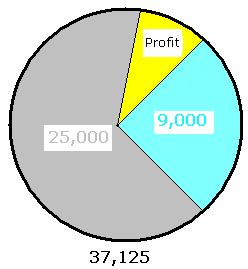
4.1.2 Problem 3 : A shop keeper makes a business of Rs 37,125 in
a month. He spends Rs 25,000 for purchase of items. He pays Rs 9000 towards
rent, salary to employees and other expenses. Find the profit or loss
percentage
Solution
:
|
His
expenses (equivalent to CP) are Rs 34,000(=25,000+9000) His
income (equivalent to SP) = 37,125 Since
SP>CP, he has a made a profit of SP-CP= 37,125-34,000 = 3125
|
|
If we are given selling price(SP) and profit or loss % ,
we can find cost price by the formula
CP = 100*SP/(100+Profit%) when there is a profit
CP = 100*SP/(100-Loss%) when there is a loss
4.1.2
Problem 4: A fruit seller cuts a papaya into 12pieces
and sells each piece at Rs 2.50.If he gains 50% find the cost price of papaya
fruit
Solution
:
|
Since
Papaya fruit is cut in to 12 pieces and selling price of each is Rs 2.50 Selling
price of papaya(SP) = 2.50*12 = Rs 30. His
profit% is given as 50. We are required to find CP Since
he has made a profit of 50% CP = 100*SP/(100+Profit%) = 100*30/(100+50) =
100*30/150 = 20 Rs Veification: SP =30
and CP=20
|
|
4.1.2
Problem 5:
If a vegetable vendor sells 10 Kg of beans at
Rs71.25 and incurs a loss of 5%, What is his cost price?
Solution
:
Since he has made loss of 5%
CP = 100*SP/(100-Loss%) = 100*71.25/(100-5) = 100*71.25/95
= 75Rs
Veification:
SP =71.25 and CP=75
Loss = CP-SP =
75-71.25 = 3.75 Rs
Loss % = Loss*100/C.P
= 3.75*100/75 = 5% which is the loss% as given.
If we are given Cost price(CP) and profit or loss % , we
can find List price by the formula
SP = (100+Profit %)*CP/100 when there is a profit.
SP = (100-Loss %)*CP/100 when there is a loss.
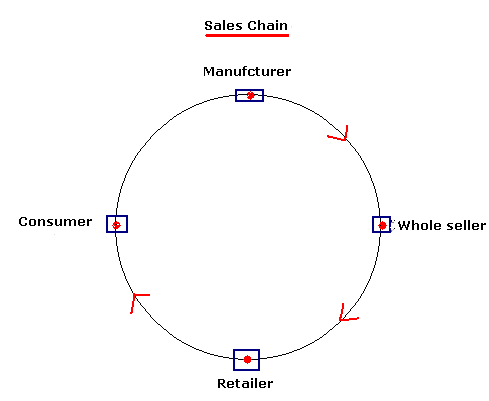
4.1.2
Problem 6: Let us understand how an item manufactured by
a manufacturer reaches a buyer. Firstly, the item is manufactured by a
manufacturer. Then, the manufacturer sells the items to a Wholesale merchant.
Then the wholesale merchant sells the
items to retailers. Finally retailer sells the item to Buyer.
|
|
A manufacturer gains 50% on each item when an item is sold
to a wholesale merchant. Wholesale merchant gains 25% on each item sold to
retailer. Retailer gains 10% on each item sold to a buyer. If cost of
manufacturing an item is Rs 200. Find
out the price paid by an individual.
Solution
:
We need to find SP of an item by Manufacturer, Wholesale
Merchant and Retailer.
Since each one is making a profit we need to use the formula:
SP = (100+Profit %)*CP/100
SP of a manufacturer = (100+50)*200/100 = 300Rs ( CP of a Manufacturer is 200)
SP of a Wholesale merchant = (100+25)*300/100 = 375Rs ( CP of a Wholesale merchant is 300)
SP of a Retailer = (100+10)*375/100 = 412.50 Rs ( CP of a Retailer is 375)
Veification:
Let us find gain for Manufacturer ,Wholesale merchant,Retailer:
For Retailer SP =412.50 and CP=375
Profit = SP-CP =
412.50-375 = 37.5
Profit % =
Profit*100/C.P = 37.5*100/375 = 10% which is the gain as given.
For Wholesale merchant
SP =375 and CP=300
Profit = SP-CP =
375-300 = 75
Profit % =
Profit*100/C.P = 75*100/300 = 25% which is the gain as given.
For Manufacturer SP
=300 and CP=200
Profit = SP-CP =
300-200 = 100
Profit % =
Profit*100/C.P = 100*100/200 = 50% which is the gain as given.
4.1.2
Problem 7: By selling an article for Rs 23 a man lost 8%.
At what price should he sell it to make a profit of 10%?. What is the cost
price of the article?
First we need to calculate CP and then find SP
Solution
:
Since man has lost 8% by selling at Rs 23.
CP = 100*SP/(100-Loss%) = 100*23/(100-8) = 100*23/92 = Rs
25
Since he has to make a profit of 10% on a CP of Rs 25
SP = (100+Profit %)*CP/100 =
(100+10)*25/100 = 110*25/100 = Rs.27.5
Veification:
When the man sold at a loss
CP =25, SP =23: loss = CP-SP = 25-23 =2
Loss % = Loss*100/C.P =
2*100/25 = 8% which is the loss% as given when he sold the article at Rs.23
When he makes a profit SP=27.5(as Arrived at above) and
CP is still =Rs25
he has made a profit = SP-CP = 27.5-25 = 2.5
Profit % =
Profit*100/C.P= 2.5*100/25 =10% which is as given
4.1.2
Problem 8: A merchant purchased 1000 cucumbers for
Rs.3800.He paid 2% tax and spent Rs.50 on transportation.40 of them were
spoiled. At what price should he sell the remaining to gain Rs.1114 on the
whole?
Solution
:
Since we want to know his SP, first we need to calculate
the CP. The CP should include his purchase price, tax and transportation.
Purchase price of 1000 cucumbers =
3800
Tax at 2% on RS 3800 = 3800*2/100 = 76
Transportation cost = 50
Total CP =
3926
SP = CP+ profit = 3926+1114 = 5040
Since 40 cucumbers were spoilt he could sell only 960
His rate of sale of
cucumber = 5040/960 = Rs 5.25
Veification:
SP = no of
cucumbers * rate = 960*5.25 = 5040
Profit = SP-CP = 5040-3926 = 1114 which is as given in the
Problem
4.1Summary of learning
|
No |
Points to remember |
|
1 |
Profit
= CP-SP (When SP>CP) |
|
2 |
Loss =
SP-CP (When SP<CP) |
|
3 |
Profit
% = Profit*100/C.P |
|
4 |
Loss %
= Loss*100/C.P |
|
5 |
CP =
100*SP/(100+Profit%) (when there is a
profit) |
|
6 |
CP =
100*SP/(100-Loss%) (when there is
a loss) |
|
7 |
SP =
(100+Profit %)*CP/100 (when there is a
profit) |
|
8 |
SP =
(100-Loss %)*CP/100 (when there is
a loss) |
Additional
Points:
4.1.2 Problem
9: A man sells a
TV set for Rs 6900 and makes a profit of 15%. He sells a second set at a loss
of 10%. If on the whole he neither gains nor loses, find the cost price of the
second TV set.
Solution:
SP = 6900. Profit% = 15
We know CP = 100*SP/(100+Profit%). By substituting values
we get,
CP
= 100*6900/115 = 6000
We also know that Profit = CP-SP and hence
Profit = 6900-6000 = 900
Since in all he does not make any profit or loss, it is
clear that he incurs a loss of Rs 900 while selling the second set.
We know
Loss % = Loss*100/C.P
Therefore
10 = 900*100/CP
And hence CP = 9000
Thus the cost price of second TV set is Rs 9000.
4.1.2 Problem
10: A man bought two transistors which costed him
Rs 720. He sold one of them at a loss of 15% and the other at a gain of 19%. If
the selling price of both transistors is same find the cost price of each
transistor.
Solution:
Let x be the cost price of first transistor.
The cost price of
second transistor is 720-x.
When sold at a loss we know
SP = (100-Loss %)*CP/100
SP = (100-15)*x/100 = 85x/100
Since the 2nd transistor was sold at profit we know
SP = (100+Profit %)*CP/100
SP = (100+19)*(720-x)/100 = 119*(720-x)/100
Since SP of both transistors is same, we have
85x/100 = 119*(720-x)/100
i.e. 85x =
119(720-x) = 119*720 - 119x
i.e. 85x+119x = 119*720
i.e. 204x = 119*720
x = 119*720/204 = Rs 420 which is the cost price of first
transistor
The CP of second
transistor = 720-x = 720-420 = Rs 300
Verify
that above working is correct.