3.1  Introduction to Sets:

 

A class has 60 students. Every one should choose to be in Kabadi team or hockey team or in both the teams. If 45 students chose to be in Kabadi team  and 30 students chose to be in Hockey team, how many are in both the teams?

 

Can you answer the above question quickly? We find answer to this question in the topic 3.3.

Study of sets helps us to solve problems similar to the given above

 

Definition: A ‘set’ is a collection of well defined objects. The objects which are members of the set are called elements. The elements of a set are listed within { }

A = {1, 4, 9, 16…}

B= {1, 8, 27, 64…}

 

A set can be represented either by listing elements or by the rule.

The above set A can also be represented as

C = {Perfect square numbers}

D = {Perfect cube numbers}

The method by which we list the individual elements of the set is called ‘roster method’ as is the case with sets A and B

The method by which we describe the set by specifying the common property of the elements of set is called ‘rule method’ as is the case with sets C and D.

 

Notes:

1. Definition of the set should be such that the objects are easily identifiable. With the clear definition, it should be possible to conclude whether an object belongs to the set or not. ‘Collection of tall people’ can not be a set; because the subjective word ‘tall’ can not identify people. However group of people whose height is more than 175cm is a set.C = {set of people whose height >175cm}.With this definition, we can clearly say whether a person belongs to the set or not.

 

2. Listing of elements in a set in an orderly or logical manner is not important.

For example, E = {1, 4, 9, 16…} is same as {4, 9, 16, 1, ..}.

 

3. An element need not be listed more than once even if the element is repeated.

For example, F ={1,2,3,4 } is same as {1,2,3,3,4}

 

Let X = {x:  x is an odd number such that 2<x<10}

The odd numbers are 1, 3,5,7,11,13….

Since the definition of X is such that the odd number has to be < 10 and > 2

X = {3, 5, 7}.

We note that 3 is an element of set X (We say that 3 belongs to X and symbolically this is denoted by 3  X.).

Though 11 is an odd number it is not an element of X (We say that 11 does not belong to X and symbolically this is denoted by 11  X).

Are 1900 and 2000 leap years?

Since 1900 is divisible by 4 and also divisible by 100, 1900 is not a leap year.

Since 2000 is divisible by 4 and it is also divisible by 400, 2000 is a leap year

Hence, 1900  {Leap Years} and 2000  {Leap years}

Have you noticed that, we can not count the number of elements in the set E?

However in case of set X, we could count the number of elements which is = 3

Definition: A finite set is a set which has countable number of elements. An  infinite set is a set whose elements are not countable (They have infinite number of elements).

Can a set have no elements (Zero number of elements) ?

Observe

Y = {number of human beings on moon}

Z = {z : z is a prime number  between  8 and 10}

These two sets do not have any element at all.

Definition: A set which has no elements is called an empty set or null set.

Null set is denoted by { } or  (pronounced as ‘phi’).

Note that {0} is not a null set as it has one element 0 in it.

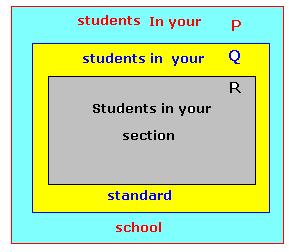
Let us consider the following examples P = {Students of your school} Q = {Students of your standard} R = {Students of your section} Is there a relation ship between these three sets? 1. ‘Students of your section’ are also ‘Students of your standard’ and ‘Students of your standard’ are also ‘Students of your school’, 2. Set P has more elements than the number of elements in Q and set Q has more elements than R. In simple terms, P is bigger than Q and Q is bigger than R. Mathematically we say that R is a sub set of Q and Q is a sub set of P and their relationship is symbolically represented as R    Q and Q   P.  is pronounced as ‘sub set’ The parent set P is called a universal set of Q and R.

 

Definition : If  A  and B are two sets such that every element of B is also an element of A, then we say, B is a ‘sub set’ of A. Their relationship is written as B  A.

Definition : The main or the bigger set  from which elements are taken out to form subsets is called the ‘universal set’ and is denoted by U.

 

Note that the universal set contains all the elements of all the sub sets under consideration. All sub sets are derived from universal set.

 

Let X= {1,3,5,7}

Does  {3,5,7,1}  X ? Yes it is

What about the null set?  Since null set does not have any element, it is a subset of every set.

Every set is a sub set of itself.  Every set   itself

An empty set is a sub set of every set.   every set

Definition:  A set having a single element is called a ‘singleton set’

P = {Set of even prime numbers},   X = {Identity element of addition}, Y= {1} are all examples of singleton sets.

Let Q =

Then   is a sub set of Q (When a set has no elements, we have 1 sub set)

Let   P = {p, q)

Then P₀ =, P₁ = {p}, P₂ = {q} and P = {p, q) are all the subsets of P (When a set has 2 elements we have 4 sub sets)

Let A = {a, b, c}

A₀ =, A₁ = {a}, A₂ = {b} A₃ ={C}, A₄ = {a, b}, A₅ = {b, c}, A₆ ={c, a} and A = {a, b, c} are all the subsets of A. (When a set has 3 elements we have 6 sub sets)

 

In topic 1.1 we have studied different type of numbers and let us try to represent them using set notations.   If     N = {Set of natural numbers},     W={Set of whole Numbers},     Z= {Set of integers} and     Q= {set of rational numbers}     Then  N  W  Z   Q     Note All these are infinite sets.

 

 

 

 

 

3.1 Summary of learning

 

 

No	Points learnt
1	Definitions of Finite set, Infinite set, Elements, Null set, Sub set, Universal set