3.3 Sets- Part 2:

Introduction: Is it not interesting to solve a problem similar to:

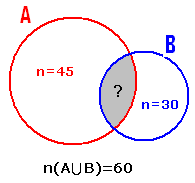
“A class has 60 students. Every one should choose to be in Kabadi team or hockey team or in both the teams. If 45 students chose to be in Kabadi team and 30 students chose to be in Hockey team, how many are in both the teams”

In this chapter we solve similar problems.

3.3.1 Properties of sets:

We know that 2+3 =3+2 and 2*3 =3*2.

Thus addition and multiplication are commutative.

Similarly (2+3)+4= 2+(3+4) and (2*3)*4= 2*(3*4).

Thus addition and multiplication are associative.

Let us study these properties for sets

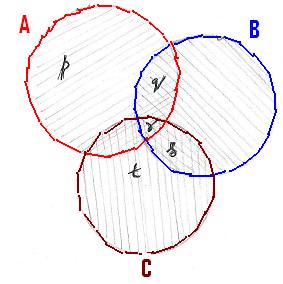
3.3.1 Example 1 : Let us consider the sets A = {p,q,r,} ,B = {q,r,s,} and C={r,s,t}

Prove that

1. BC =CB

2. BC = CB

3. A(BC) = (AB)C

4. A(BC) = (AB) C

5. A (BC) = (AB) (AC)

6. A (BC) = (AB)(AC)

BC = {q,r,s}{r,s,t} = {q,r,s,t} ------à(1)

CB = {r,s,t} {q,r,s} ={q,r,s,t} -------à(2)

From (1) and (2) we conclude that BC =CB

1. Union of sets is commutative

BC = {q,r,s}{r,s,t} = {r,s} -----à(3)

CB = {r,s,t} {q,r,s} = {r,s} -----à(4)

From (3) and (4) we conclude that BC = CB

2. Intersection of sets is commutative

AB = {p,q,r,}{q,r,s} = {p,q,r,s}

A(BC) = {p,q,r} {q,r,s,t} ={p,q,r,s,t,} ---à(5)

(AB)C= {p,q,r.s}{r,s,t} = {p,q,r,s,t} ---------à(6)

Since (5) and (6) are same A(BC) = (AB)C

3. Union of sets is associative

AB = {p,q,r}{q,r,s} = {q,r}

A (BC) ={p,q,r}{r,s} ={r} ------à(7)

(AB) C = {q,r}{r,s,t} = {r} ------à(8)

Since (7) and (8) are same A(BC) = (AB) C

4. Intersection of sets is associative

A (BC) = {p,q,r}{r,s} = {p,q,r,s} -----------------à(9)

AC = {p,q,r}{r,s,t} = {p,q,r,s,t}

(AB) (AC) = {p,q,r,s}{p,q,r,s,t} ={p,q,r,s} ----à(10)

Since (9) and (10) are same A (BC) = (AB) (AC)

5. Union of sets is distributive over intersection of sets

A (BC) = {p,q,r,}{q,r,s,t} ={q,r} ----à(11)

(AB) = {p,q,r}{q,r,s} = {q,r}

(AC) = {p,q,r}{r,s,t} = {r}

(AB)(AC)= {q,r}{r} = {q,r} --------à(12)

Since (11) and (12) are same A (BC) = (AB)(AC)

6. Intersection of sets is distributive over union of sets

De Morgan’s laws

Prove that

1. (AB)¹= A¹B¹ (The complement of union of sets is the intersection of their complements)

2. (AB)¹= A¹B¹(The complement of the intersection of sets is the union of their complements)

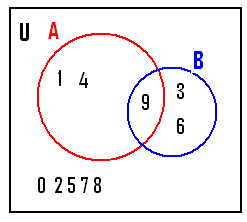
3.3.1 Example 2 : Let U = {0,1,2,3,4,5,6,7,8,9}:A = {x: x is a perfect square less than 10}:B = {x: x is a multiple of 3 less than 10}

Let us write the elements of the sets A and B

A = {1,4,9} (other numbers are not squares of any number)

B = {3,6,9} (3 = 3*1, 6=3*2,9=3*3)

A¹= U-A ( A¹ contains elements of U which are not the elements of A)

= = {0,1,2,3,4,5,6,7,8,9} - {1,4,9} ={0,2,3,5,6,7,8} =========à(1)

B¹= U-B ( B¹ contains elements of U which are not the elements of B)

={0,1,2,3,4,5,6,7,8,9} - {3,6,9} ={0,1,2,4,5,7,8} =========à(2)

From (1) and (2) we get

A¹B¹= {0,2,3,5,6.7,8}{0,1,2,4,5,7,8} ={0,2,5,7,8} ==================à(3)

(AB) = {1,4,9}{3,6,9} = {1,3,4,6,9}

(AB)¹= U -(AB) = {0,1,2,3,4,5,6,7,8,9}- {1,3,4,6,9} = {0,2,5,7,8} ==à(4)

Since (3) and (4) are same

1. (AB)¹= A¹B¹

From (1) and (2) we get

A¹B¹= {0,2,3,5,6,7,8}{0,1,2,4,5,7,8} ={0,1,2,3,4,5,6,7,8}==============à(5)

AB = {1,4,9}{3,6,9}= {9}

(AB)¹= U – (AB) = {0,1,2,3,4,5,6,7,8,9}- {9} ={0,1,2,3,4,5,6,7,8} =======à(6)

Since (5) and (6) are same

2. (AB)¹= A¹B¹

3.3.2 Relationship between numbers of elements of 2 sets

The number of elements in a set A is called ‘cardinal number’ of the set and is denoted by n(A).

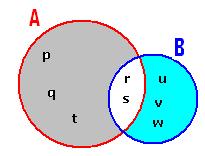
3.3.2 Example 1 : Let A= {p,q,r,s,t} and B= {r,s,u,v,w}

n(A) =n(B)=5

AB ={p,q,r,s,t}{r,s,u,v,w}= {p,q,r,s,t,u,v,w}

AB ={p,q,r,s,t}{r,s,u,v,w} =(r,s} n(AB) =8, n(AB) =2

n(A) +n(B) = 5+5 =8+2 = n(AB) +n(AB)

These equations can be re written as

1. n(AB)= n(A) +n(B)-n(AB)

2. n(AB)= n(A) +n(B)-n(AB)

3. When A and B are disjoint sets n(AB)= n(A) +n(B)

( n(AB)=0 as AB is a null set when A and B are disjoint sets).

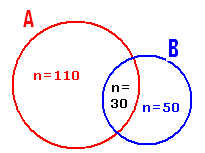
3.3.2 Problem 1: A florist has certain number of garlands. 110 garlands have Champak flowers in the garlands, 50 garlands have jasmine flowers in the garlands and 30 garlands have both the flowers in them. Find the total number of garlands he has.

Solution :

Let A be the set having garlands having Champak, therefore n(A) =110.

Let B be the set of garlands having Jasmine, therefore n(B)= 50.

AB is the set of garlands which has both these flowers. Therefore n(AB)=30.

AB is the set of garlands the florist has.

We know n(AB)= n(A) +n(B)-n(AB) = 110+50-30 =130

Therefore the florist has 130 garlands.

3.3.2 Problem 2: A class has 60 students. Every one should choose to be in Kabadi team or hockey team or in both the teams. If 45 students chose to be in Kabadi team and 30 students chose to be in Hockey team, how many are in both the teams?

Solution :

Let A be the set of students who are in Kabadi team. Therefore n(A) =45

Let B be the set of students who are in Hockey team. Therefore n(B) = 30

AB is the set of students who are in both the teams.

We are asked to find n(AB).

AB is the set of students in the class. It is given that n(AB)=60

We know that n(AB)= n(A) +n(B)-n(AB) n(AB)= n(A) +n(B)- n(AB)= 45+30-60 =15

15 students have taken both Mathematics and Science.

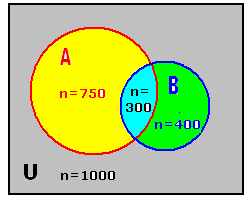
3.3.2 Problem 3 :A TV viewer ship survey was conducted by an agency. They conducted a survey on a sample of 1000 families in a place. They found that 750 families viewed News channel, 400 families viewed sports channel and 300 Families viewed both channels.

Find out

1. How many families viewed News channel only?

2. How many families viewed Sports channel only?

3. How many families viewed neither of the channels?

Solution :

Let U be the set of families who were surveyed

Let A be the set of families who viewed News channel. (A) =750

Let B be the set of families who viewed Sports channel. n(B)=400

AB is the set of families who viewed both news and sports channel. n(AB)=300

Notes:

1. A-AB is the set of families who see only News channel and its numbers is n [A-AB].

2. B- AB is the set of families who see only Sports channel and its numbers is n [B-AB].

3 AB is the set of families who see either News or Sports channel. its numbers is

n(AB)= n(A)+n(B)-n(AB)= 750+400-300 = 850

4. (AB)¹ is the set of families who neither see News nor Sports and its numbers is n(AB)¹

We have:

1. n [A-AB] = n(A) – n(AB) = 750 -300 = 450(Only news Channel viewers)

2. n [B-AB] = n(B) – n(AB) = 400 -300 = 100(Only Sports Channel viewers)

3. n(AB)¹= n[U – (AB)] = n(U) – n((AB)) = 1000-850 = 150( who do not view 2 channels)

3.3 Summary of learning

No	Points to remember
1	(AB)¹= A¹B¹
2	(AB)¹= A¹B¹
3	n(AB)= n(A) +n(B)-n(AB)
4	n(AB)= n(A) +n(B)-n(AB)

Additional Points:

Let us assume that you have been given the following question in an examination for matching.

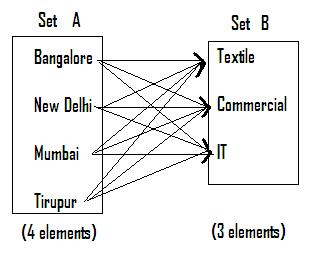
From examination point of view there can only be three right matches. However, as it can be seen from the figure (Every elements in set A is paired with every element in set B), we have 12 possible pairs. Thus we have in all 4*3 = 12 possible pairs.

Observe that (Bangalore, IT) (IT, Bangalore)

If A and B are two given sets, the set containing all the ordered pairs where the first element is taken from A and the second element taken from B is called ‘Cartesian product’ of two sets. The resulting set is denoted by AB (read as A cross B).

AB = { (x,y) : x A and y B}

Observe in the above figure that (Bangalore, IT) (IT, Bangalore)

Since (a,b)(b,a) AB BA

Note that n(AB) = n(A)*n(B)

Some times when we have an ordered pair, it is possible to have a relationship between elements of two sets. Some of these relations are =, <,>, ||.

A ‘relation’ is a set of ordered pair which explains how elements of one set are related to elements of other set and the relation is normally denoted by R. Let

A = {Uttar Pradesh, Andhra Pradesh, Bihar, ..}

B = {Bhubaneswar, Ahmadabad, Calcutta, Chennai,….}

We can have a relationship called ‘state’s capital is’.

Then the meaningful relationships are {(Orissa, Bhubaneswar), (Bihar, Patna), (Gujarat, Ahmadabad),….}

Note that (Bihar, Patna) (Patna, Bihar) as the relationship changes from ‘State’s capital is’ to ‘is capital of the state’.

Their Name:
Their Email:
Your Email:
Your Name:
Your message to your friend: