1.8 Progressions of numbers:
Will it not be interesting to solve a puzzle
similar to the one given below?
Puzz1e
1:
Suppose you had taken a loan of Rs.10, 000 from a friend
and you agree to pay few Rupees every day. You have following options to choose:
1.
You
repay the loan at the rate of Rupee a day. Do you think your friend will agree
for this? He may not agree. (Because repayment will take nearly 28 years
(10000/365))
2.
You
agree to pay the amount equal to the day of payment (1st day 1Rs, 2nd
day 2Rs, 3rd day 3Rs. 4th day 4Rs..). Will you agree to
pay for indefinite number of days?
3.
First
day you pay 1Rs and subsequently you pay twice the amount of previous day(1st
day 1Rs, 2nd day 2Rs, 3rd day 4Rs, 4th day
8Rs..) Will you agree to pay for indefinite number of days?
In the case of last 2 options don’t you need to know the
number of days of repayments?
Puzz1e
2: You decide to participate in a
Cycling race of 70km. In the first hour
of race you cycle at the rate of 16km/hr. If your cycling speed reduces by 1km
every hour thereafter, find out how much time you require to complete the race?
Let us see how mathematics can help us in finding
solutions to these real life problems.
1.8.1 Sequence:
1.8.1
Example 1: If you
are asked to list out all the classes in your school. What will you write?
Will you write the list as 3,10,4,1,12,8,7,5,6,2,9,11?
No, You will probably write them as
1,2.3,4,5,6,7,8,9,10,11,12
1.8.1
Example 2:
Similarly if you are asked to write the dates of Sundays in January 2006 you will
write them as?
1, 8,15,22,29
What did you do? Without being aware you applied a rule in
both the cases.
In the first case you started with 1st standard
and applied the rule of ‘one more than previous number’ to list other classes.
You stopped at 12 as it was the last standard in your school.
Similarly in the 2nd case you found that first
Sunday of January 2006 is 01 and applied the rule ’add 7 to previous number
till the date is less than31’. You stopped at 29 as any month does not have more than 31 days. But if you were
asked to find the Sundays in February of a year, you will apply a different
rule, depending upon whether the year is a leap year or not.
Observe the following list
1.8.1
Example 3 :
2,4,6,8,10,12……..
What did you notice? It is a list of even numbers and the
list does not end at all
Definition : A sequence is an ordered arrangement of numbers according
to a rule.
The individual numbers in the sequence are called ‘terms’
of the sequence.
The terms of a sequence are
generally denoted by T1 T2T3T4T5
…. as shown below
|
Order
number of the term ==à |
1st |
2nd |
3rd |
4th |
---- |
nth |
--- |
|
Corresponding
notation ===à |
T1 |
T2 |
T3 |
T4 |
---- |
Tn |
--- |
The sequence is generally denoted (represented) by {Tn }
A sequence which has definite number of terms is called a ‘finite sequence’,
If the sequence which has indefinite number of terms is
called a ‘infinite
sequence’,
In the first example we had 12 terms and in the 2nd
example we had 5 terms and hence both of them are examples of finite sequence.
The list of even numbers does not have finite number of
terms and hence it is an infinite sequence.
1.8.1
Example 4 : The
sequence can also be of fractions like
2/1 , 3/2 , 4/3, 5/4 ,,,,,,,,
What is the general term Tn here?
We observe
T1 = (1+1)/1
T2 =(2+1)/2
T3 =(3+1)/3
T4 =(4+1)/4
Thus
Tn=(n+1)/n .With this general
representation of the nth term we can find any term of the sequence.
Hence the 6th term isT6 =(6+1)/6 =7/6
1.8.1
Problem 1 : If Tn =2n2+1 find the value of n
if Tn=73
We have Tn =2n2+1 =73; 2n2
=73-1=72: 2n2 =72 : n2 =36: n = ![]() =
=![]()
Since it is a natural number, it has to be positive and
hence n=6.
Verify that T6 = 2*62+1 = 2*36+1=73
1.8.2 Series
Definition : The sum of terms of a sequence is called the series of
the corresponding sequence and is usually denoted by S or Sn.
Observe
that sum of the series is meaningful for
finite sequence, as summing up terms of an infinite sequence is meaningless. (In
later sections you will learn about infinite series whose sums are meaningful).
Sn = T1 + T2+T3.........Tn
Prove that Tn =Sn- Sn-1
We have Sn- Sn-1=(
T1 + T2+T3.........Tn-1+ Tn) -( T1 + T2+T3.........Tn-1)=
Tn
1.8.2
Problem 1 : If Tn ={(-1)n} prove that S1
= S3 : S2 = S4
Since Tn =(-1)n
we have
T1= (-1)1 = -1, T2 = (-1)2
=1, T3 = (-1)3 = -1, T4= (-1)4 =
1
Substituting values for series we have
S1 = T1 = -1
S3 = T1 + T2+T3=
-1+1-1 = -1 Thus S1 = S3
S2 = T1
+ T2 =-1+1 =0
S4 =T1 + T2+T3
+T4= -1+1-1+1 =0 Thus S2 = S4
1.8.3 Arithmetic Progression:
In the Example1.8.1.1 did you notice that, the difference
between 2 successive terms of the sequence is 1 ?
Similarly what was the difference between 2 successive
terms in Example 1.8.1.2 ? It is 7.
Definition : A sequence in which the difference between 2
successive(consecutive) terms is constant is called ‘Arithmetic Progression’(AP). The Common difference which is a constant is
denoted by ‘d’
Thus by definition in an AP Tn+1 – Tn =d
and Tn-1+d = Tn
The first term of an AP is generally a constant and is
denoted by ‘a’ and hence T1 =
a
Its other terms are
T2= a+d
T3= T2+d =(a+d)+d = a+2d = a
+ (3-1)d
T4= T3+d =(a+2d)+d =a+3d= a+(4-1)d
….
General term Tn= Tn-1+d = a+(n-1)d : thus d= (Tn -a)/(n-1)
{AP}=
{a, a+d, a+2d,a+3d …, a+(n-1)d}
1.8.3
Problem 1 :Find the AP in which Sn = 5n2+3n
Solution:
Sn-1 = 5(n-1)2+3(n-1) = 5(n2 -2n+1)
+3n-3 = 5n2-10n+5+3n-3 = 5n2-7n+2
We know that Tn= Sn- Sn-1= (5n2+3n) –(5n2-7n+2)
= 10n-2
![]() T1
= 8
T1
= 8
![]() T2
=18
T2
=18
![]() T3
=28
T3
=28
So {AP} is {8,18,28…..}
Verification: S3 = T1 + T2
+ T3 =8+18+28 = 54 = 45+9 = 5*32+3*3=( 5n2+3n
with n=3)
1.8.3
Problem 2 : In an AP T10 =20 T20 =10 Find T30
Solution:
If we can find a and d we can arrive at the solution.
By definition Tn
= a+(n-1)d
Thus
T10 = a+(10-1)d = a+9d
But it is given
that T10= 20 so we have
a+9d=20: a=20-9d ====à(1)
Be definition T20 = a+(20-1)d = a+19d ====à(2)
But it is given
that T20= 10
By substituting the value of ‘a’ obtained from (1) in (2)
we get
20-9d+19d =10: 20+10d =10: 10d =(10-20)= -10: d = -1
By (1) we get a =20-9d = 20+9 =29
![]() T30
=a+(30-1)d = 29+29*(-1) = 29-29 =0
T30
=a+(30-1)d = 29+29*(-1) = 29-29 =0
Verification: Note that T10 =29+9*(-1)=20:
T20 =29+19*(-1)=10 which are the given terms.
1.8.3
Problem 3: Find
AP whose 5th and 10th terms are in the ratio of 1:2 and T12
=36
Solution:
It is given that T5 : T10 = 1:2 (i.e T5 /T10 =1/2)
![]() 2T5 = T10
2T5 = T10
By substituting generic value for T5 & T10
in the above equation
We get 2(a+4d)
= (a+9d) i.e. 2a+8d =a+9d and by transposition of terms we
get a=d.
But it is given that T12 =36
Hence a+ 11d = 36: Since a=d we get 12d =36 and hence d=3
and since a=d, a=3
Therefore the {T} = 3,6,9,12…
Verification: Note that T5 = 15 and T10 =30 which are in the
ratio of 1:2 which is the given ratio
1.8.3
Problem 4: Find
the three numbers in AP whose sum is 15 and product is 105
Solution:
Let the middle number be a. hence the first term is a-d
and the 3rd term is a+d.
Sum of three numbers = (a-d)+a+(a+d
) = 3a which is given to be 15 and hence a =5.
The product of these 3 numbers = (a-d)*a*(a+d) = a*(a2-d2) which is given to be
105
![]() a*(a2-d2)
=105
a*(a2-d2)
=105
I.e. 5(52-d2) = 105
I.e. (25-d2) = 21
I.e. 25-d2 = 21
I.e. -d2 = 21-25
I.e. -d2= -4
I.e. d2= 4
I.e. d =![]()
So the series is 3,5,7 or 7,5,3
1.8.3
Problem 5: Find
the number of integers between 60 and 600 which are divisible by 9
Solution:
The first number greater than 60 and divisible by 9 is 63
The last number lesser
than 600 and divisible by 9 is 594
Thus the sequence is 63, 72,81 ….594
Here a= 63, d=9 and Tn
= a+(n-1)d = 594
I.e. 63+(n-1)9 =
594
I.e. (n-1)9 = 594-63 = 531
![]() (n-1) = 59
(n-1) = 59
![]() n=60
n=60
Thus there are 60 numbers between 60 and 600 which are
divisible by 9
1.8.3
Problem 6: If the
mth term of an AP is 1/n and nth term
is 1/m show that its (mn)th term is 1
Solution:
Let a be the first term and d be the common difference of
AP
![]() Tm = a+(m-1)d
= 1/n and Tn = a+(n-1)d = 1/m
Tm = a+(m-1)d
= 1/n and Tn = a+(n-1)d = 1/m
By subtracting the Tm
and Tn
we get
1/n – 1/m = a+md –d –(a+nd –d)
I.e. (m-n)/mn = (m-n)d
![]() d = 1/mn
d = 1/mn
Substituting this value
of d in Tm we get
a+(m-1)/mn = 1/n
![]() a = 1/n – (m-1)/mn
a = 1/n – (m-1)/mn
= 1/mn
![]() Tmn
= a+(mn-1)d =
Tmn
= a+(mn-1)d =
(1/mn) + (mn-1)/mn =
(1+mn-1)/mn
=1
1.8.4
Summation of arithmetic series
Let us consider the puzzle discussed in the beginning
(Section 1.8). for which we wanted to find the solution
1.8.4
Problem 1 : Suppose you had taken a loan for
Rs.10,000 from a friend and you agree to
pay him, few Rupees every day. Assume
that you have two options:
Option 1: You repay the loan at the rate of 1 Rupee a day.
Do you think your friend will agree to this?
He may not, as repayment will take nearly 28 years = ![]() .
.
Option 2: You agree
to pay the amount equal to the day of payment (1st day 1Rs, 2nd
day 2Rs, 3rd day 3Rs. 4th day 4Rs and so on). Will you
agree to pay the amount indefinitely?
With the 2nd option let us find out how much
money you would have paid totally in 10 days
Total money paid after 10 days = 1+2+3+4+5+6+7+8+9+10 =
55Rs.
How do we find the money paid after 100days? Does it not take time to find out?
Let us say we are asked to find the sum of 1+2+3+. . . .
+99+100. Do not we find it difficult to add
Instead let us pair the numbers as follows:
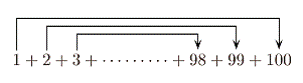
Then sum =
(1+100)+(2+99)+(3+99) . . +(50+51) =
101*50 = 5050
Let us apply this logic to find the sum of the first ‘n’
numbers of the series of natural numbers.
{T} = {1,2,3……n}
Sn = 1 + 2 + 3 ………….+(n-2)+
(n-1) +n(there are n terms)
+ Sn = n +(n-1)+(n-2) … +
3
+ 2 +1(repeated in reverse order)
==================================
2Sn= (n+1)+(n+1)+(n+1)
….. .+(n+1)+(n+1)+(n+1)
(there are n terms) = n(n+1)
![]() Sn=
Sn= ![]()
Using this formula in the above problem, let us cross
check the correctness of the amount paid by you after 10 days:
S10 =10*11/2=
55 Rs which is correct!
Now Let us find the amount paid by you after 100 days: S100
= 100*101/2 = 5050 Rs
Do you think you will require 200 days to clear the loan? :
S200 = 200*201/2 =20,100 Rs
In 200 days you would have paid 10,100 Rs extra! This is a
trial and error method. (In next sections you will learn to find the value of n
satisfying the condition n(n+1) =1000)
For now, note S141 = ![]() =10,011
=10,011
So you require 141 days to return the loan.
The above sum (Sn )
is also denoted by the symbol ![]() =
= ![]()
Definition: A series whose terms are in AP is
called an ‘arithmetic
series’ For example:
{2,5,8}, {1,4,7,},
{3,7,11}
Find the first ‘n’
terms of an AP:
{AP}= {a, a+d, a+2d, a+3d
….,a+(n-1)d}
Sn= [a+(a+d)+(a+2d)+(a+3d)
…..a+(n-1)d] = [a+a+a ….(n times) +d(1+2+3+ +(n-1)] = na+d[![]() ] =
] =
na+ ![]() (apply the formula by
replacing n by (n-1) in
(apply the formula by
replacing n by (n-1) in ![]() )
)
Sn = na+ ![]() =
= ![]() = n*(
= n*(![]() )
)
= n*(![]() )=n*(
)=n*(![]() )
)
Let us use the above formula to arrive at ![]() .
.
![]() = 1+2+3+4+5+6+7+8+ . . . +n
is an AP with a =1, d=1
= 1+2+3+4+5+6+7+8+ . . . +n
is an AP with a =1, d=1
![]() Sn =
Sn =
= n*(![]() )
)
= n*(1+{1+(n-1)*1}/2
= n*(n+1)/2
This is the same formula we had arrived
earlier in the beginning of 1.8.4.
1.8.4
Problem 2 : Find the sum of arithmetic
series which contains 25 terms and whose middle term is 20
Solution:
Given : n=25, T13 =20, we are required to find S25
But T13 = a+12d
S25 =
n*(a+ T25)/2= 25*(a+a+24d)/2 = 25*2*(a+12d)/2 = 25*(a+12d) = 25*20(![]() T13 = a+12d) = 500
T13 = a+12d) = 500
1.8.4
Problem 3 : Find the sum of all natural
numbers between 101 and 201 which are divisible by 4
Solution:
{AP} = (104,108,112 …200}
Sn = 104+108+112+……
= 104+(104+4) +
(104+8)… (104+96) (104 repeats 25 times)(Note that 1st term =104,
last term is 200 and difference = 4
![]() we have 24 =
we have 24 =![]() terms after the first
term, Thus in all 25 terms)
terms after the first
term, Thus in all 25 terms)
= 104*25
+4(1+2+3…..24)
= (104*25) +4*(![]() )
)
=2600+1200=3800
1.8.4
Problem 4 :
Assume you went on a trip to Shravanabelagola
where the statue of Bahubali, carved out of a
single stone is installed. Assume that
you climbed 23 steps in the first minute. After that you started climbing 2
steps less than what you had climbed in the previous minute. If you reached a
resting place after 7 minutes of climbing, find out how many steps did you
climb before reaching the resting place?
Solution:
Notice that you are climbing 2 steps
less than the previous minute. Hence your steps of climbing are an AP.
Since you have taken 7 minutes to reach the resting place, we are required to
find S7 of an AP.
{AP} = {23,21,19….) so we have a=23 and d = -2
Since Sn of an AP = n*(![]() )
)
![]() S7
S7
= 7* (![]() )
)
= 7*[46-12]/2
= 7*17 = 119
Exercise: If you need to climb 1000 steps
to reach the statue, find out how much time you will require to reach the statue?
1.8.4
Problem 5: You decide to participate in a Cycling race of
70km. In the first hour of the race you
cycle at the rate of 16km/hr. If your cycling speed reduces by 1km every hour
thereafter, find out how much time you require to complete the race.
Solution:
Notice that your cycling speed is (16,15,14, …) which is
an AP. We are required to find n such that Sn
=70
In the given AP, note that a =16 and d = -1
Since Sn = n*(![]() )
)
= n*(![]() )
)
= n*(![]() )
)
= n*(![]() )
)
n*(![]() ) = 70(
) = 70(![]() total distance =70km)
total distance =70km)
Thus we have an
equation to solve
(33n-n2
) = 2*70=140 or
-n2 +33n -140 =0 or
n2 -33n
+140 =0 or
(n-5)*(n-28) = 0
Thus n=5 or n=28
As per this solution the distance is covered in 5 hours or
28hours.
Though mathematically we have 2 answers to the same
problem, we have to eliminate one answer in this real life problem.
Let us observe the 28th term of this AP
Tn=
a+(n-1)d so
T28=
16+(28-1)*(-1) = 16-27 = -11
Since the cyclist can not cycle in a negative speed, n=28
is not a correct answer to the real life problem.
Thus the correct answer is 5 hours.
1.8.4
Problem 6: To catch a herd of elephants, a king starts
the journey starting with 2 ‘Yojana’s( unit of
distance) on the first day. O genius, tell me the increase in distance he has
to cover every day, if he takes 7 days
to cover the total distance of 80 ‘Yojana’s ( Lilavati Shloka 126 ).
Solution:
The distance covered by the king is an AP, with a =2, n=7 and Sn
=70. We need to find d
Sn = n*(![]() )
)
= 7*(![]() )
)
= 7*(![]() )
)
= 7*(2+3d) = 80
![]() 2+3d = 80/7
2+3d = 80/7
![]() 3d = (80/7)-2 = (66/7)
3d = (80/7)-2 = (66/7)
![]() d = (80/7)-2 = (22/7)
d = (80/7)-2 = (22/7)
Thus the king needs to increase the distance covered every
day by (22/7) Yojanas.
1.8.4
Problem 6: A person gifts every day 3 Pallas (A
unit of measurement of volume) of grains and increases it by 2 Pallas
every day, O Lilavati tell me the number of days needed
to gift 360 Pallas.
( Lilavati
Shloka 124
)
Solution:
The grains gifted by the person is an AP, with a =3, d=2 and Sn
=360. We need to find n
Sn = n*(![]() )
)
= n*(![]() )
)
= n*(3n+2n-2) = n(n+2)
![]() n2+2n =360
n2+2n =360
![]() n2+2n -360
=0
n2+2n -360
=0
![]() (n+20)*(n-18) =0
(n+20)*(n-18) =0
![]() n= -20 or n =18
n= -20 or n =18
Since number of days can not be negative, the person needs
18 days to gift the entire 360 Pallas.
1.8.5 Geometric Progression (GP):
Let us take some examples
1. {T}= {2,4,8,16
…….}. In this series we observe that any
term is twice the previous term. I.e. next term = 2* previous term or previous
term = ½ of next term. The ratio of the terms = 1:2.
2. {T}= {27,9,3,1
…….}. In this series we observe that any
term is one third the previous term. I.e.
next term = 1/3* previous term or previous term = 3times the next term.
The ratio of terms =3:1
Definition : A sequence whose ratio of term and its preceding or
succeeding term is constant is called ‘Geometric Progression(GP)’
Thus by definition, in a GP Tn /Tn-1 = constant. In the
first case T3 /T2=![]() =2 and in the 2nd case T3 /T2=
=2 and in the 2nd case T3 /T2=![]() = 1/3
= 1/3
In a GP if the first term T1 = a and the ratio
is r we have
T2= T1*r= ar(2-1)
T3= T2*r= ar*r
=ar2= ar(3-1)
T4= T3*r= ar2*r = ar3=
ar(4-1)
In general Tn= ar(n-1)
In a GP we also know that Tn=
Tn-1*r
So {a, ar, ar2, ar3
……….. ar(n-1)} is the standard form of GP.
1.8.5
Problem 1 : In a
GP 7th term is eight times the fourth term and the 5th
term is 12 find the GP if S10: S5= 33:1 and T6= 32
Solution:
Tn = arn-1
![]() T7=a r6
and T4=a r3 it is
also given that T7= 8T4
T7=a r6
and T4=a r3 it is
also given that T7= 8T4
![]() a r6= 8a r3
a r6= 8a r3
![]() r3= 8
r3= 8
![]() r=2
r=2
We know T5=a r4
= a 24=16a
=12 (given)
![]() a =
a = ![]() =
=![]()
Therefore {GP} = {![]() ,
, ![]() *2,
*2, ![]() *22 ,
*22 , ![]() *23….} = {3/4, 3/2,3,6…}
*23….} = {3/4, 3/2,3,6…}
Let us find the sum
of n terms of a GP = {a, ar,
ar2, ar3 ……….. ar(n-1)}(n
terms)
(1) Sn=
a +ar+ar2+ ar3 ……….. +ar(n-1) By
multiplying this equation by r we get
(2) rSn=
ar+ar2+ ar3 …… +ar(n-1)+
arn
Subtracting (2) from (1) we get Sn- rSn=a- arn
I.e. Sn(1-r) =a(1- rn)
Sn= a (1- rn) / (1-r)
-----à
we use this formula when r <1
= -a (1- rn) /-(1-r) (multiply numerator and denominator
by -1)
=
a ( rn-1) / (r-1)
-----à
we use this formula when r >1
What are the possible values of r ? ( r=1, r>1,r<1)
1) If r=1 then GP = {a ,a,a.a,a….}
2) When r<1.
Let us arrive at few terms of the GP when r = ![]() = 0.9 and n is very
large.
= 0.9 and n is very
large.
|
r2= |
0.81 |
|
r4= |
0.66 |
|
r8= |
0.43 |
|
r16= |
0.19 |
|
r64= |
0.0012 |
Thus when n becomes a large number rn
almost becomes zero (we say rn approaches
0).
This is true even when r is very close to 1(say 999/1000).
Sum of infinite terms of GP when r<1
Sn= a (1- rn)
/ (1-r)
When n approaches infinity we have
Sinfinity = ![]() =
= ![]()
From the above it follows that
1+(1/2)+(1/4)+(1/8)+(1/16)+………. = 1/[1-(1/2)] = 2
In a GP prove that S2n/ Sn = rn+1
S2n/ Sn
= [a(1- r2n)/(1-r)]/ [a(1- rn)/(1-r)]
= [a(1- r2n)*(1-r)]/[a
(1- rn)*(1-r)]
= (1- r2n)/
(1- rn)
= (1- rn) (1+ rn)/
(1- rn)
===à
apply the formula (a2- b2) = (a-b)*(a+b)
and note r2n= (rn)2
= (1+ rn)
1.8.5
Problem 2 : Find the sum of the finite series {
1,0.1,0.01,0.001,…. (0.1)9} (Note that the
series has 10terms and not 9 terms)
Solution:
In this problem a=1, r=1/10
We know Sn = a (1- rn) /
(1-r)
![]() S10 = 1(1- (1/10)10 ) / (1-1/10)
S10 = 1(1- (1/10)10 ) / (1-1/10)
= [(1010 -1)/1010]/(9/10)
= (1010 -1)/(9*109)
1.8.5
Problem 3 : Find
the GP if S10: S5= 33:1 and T6= 32
Solution:
We know in a GP S10: S5 = [a(r10-1)/(r-1)]/
[a(r5-1)/(r-1)]
= (r10-1)/
(r5-1)
= (r5+1) =====à apply the formula (a2- b2) =
(a-b)*(a+b) and note r10= (r5)2
= 33
(given)
![]() r5 =33-1=32
r5 =33-1=32 ![]() r =2
r =2
We know Tn =
arn-1
T6 = a25
= 32(given)
![]() a=1
a=1
{GP} = (1, 2, 4, 8, 16, 32,…}
1.8.5
Problem 4 : Suppose you
decide to celebrate your birthday
by distributing sweets to students of few schools. Assume that you distribute
sweets in such a way that packets given
to a school is 4 times the packets given in the previous school. To how many schools can you distribute packets, if you have 341 sweet
packets with you?
Solution:
Let us assume that the 1st school gets 1
packet.
Note that the sequence is a {GP} of {1,4,16,….} and hence
a=1, r=4. Sn = 341. We have
been asked to find n
Since r >1 We know Sn
= [a(rn-1)/(r-1)]
![]() Sn = a(4n-1)/(4-1)
Sn = a(4n-1)/(4-1)
= 1(4n-1)/3
= 341 (given)
![]() (4n-1) = 3Sn
= 3*341=1023 or 4n= 1024
(4n-1) = 3Sn
= 3*341=1023 or 4n= 1024
![]() n =5
n =5
Thus, you can distribute sweets to 5 schools.
1.8.5
Problem 5 : The
sum of the first three terms of a GP is 39/10 and their product is 1. Find the
terms and the common ratio.
Solution:
Let the first three terms be a/r, a ar
![]() (a/r)*a*ar =1
(a/r)*a*ar =1
![]() a3=1
a3=1
![]() a=1
a=1
It is given that a/r+a+ar =
39/10
![]() 1/r+1+r = 39/10(
1/r+1+r = 39/10(![]() a=1)
a=1)
![]() (1+r+r2)/r
=39/10
(1+r+r2)/r
=39/10
![]() 10(1+r+r2)=39r
10(1+r+r2)=39r
![]() 10r2-29r+10=0
10r2-29r+10=0
![]() (2r-5)(5r-2) =0
(2r-5)(5r-2) =0
![]() r =5/2 or r=2/5
r =5/2 or r=2/5
The two GPs satisfying the given conditions are
2/5, 1,5/2 Or 5/2,1,2/5
1.8.5
Problem 6: Find a
rational number which when expressed as a decimal will have 1.![]() as its expansion.
as its expansion.
Solution:
We write 1.![]() = 1.565656…
= 1.565656…
= 1+ 0.56 +.0056+.00056
= 1+a +ar +ar2+. .
. with a =.56 and r =0.01
= 1+0.56/(1-0.01)
= 1+0.56/0.99
= 1+56/99
=155/99
Thus 155/99 is the required rational number.
1.8.5
Problem 7: If a, b, c are three consecutive terms of an AP,
then show that ka kb
and kc are in GP
Solution:
Let b=a+d and c=b+d
Thus d=b-a =c-b
Hence k(b-a)= k(c-b): kb/
ka= kc/ kb
1.8.5
Problem 8: If a, b, c, d are in GP. Prove that
(b-c)2+(c-a)2+(d-b)2
=(a-d)2
Solution:
Since a, b, c , d
are in GP b =ar, c= ar2 and d = ar3
LHS = (ar –ar2)2 + (ar2-a)2+(ar3-ar)2
= a2{ r(1-r)2+(r2-1)2+
r2(r2-1)2}
= a2{ r6-2r3+1) = a2(r3-1)2
= (ar3-a)2
= (d-a)2 = RHS
1.8.5
Problem 7: If a person gifts 2 Varatakas
( A unit of measurement of money) on the first day and gives out on subsequent
days, twice the amount given on previous day, O Lilavati
tell me quickly,how much he gives out in a month?( Lilavati Shloka 130)
Solution:
The series given out
as gift { 2, 4, 8,16 . . . } is a GP. If a=2,
r =2 and n=30 we need to find out Sn
![]() Sn =
[a(rn-1)/(r-1)]
Sn =
[a(rn-1)/(r-1)]
![]() Sn = 2(230-1)/(2-1)
Sn = 2(230-1)/(2-1)
= 2(10243-1) ( ![]() 230 ={210}3=10243
230 ={210}3=10243
=
2147483646
Thus the number of Varatakas
given out as gift is 214,74,83,646.
1.8.6 Harmonic Progression:
Consider the sequences:
{![]() ,
, ![]() ,
, ![]() ,
,![]() …}
…}
{![]() ,
,![]() ,
,![]() …}
…}
By taking reciprocals of the terms of these sequences we
get
{ 3, 6, 9 12…} which
is an {AP}(Problem 1.8.3.3)
{8,18,28….} which
is an {AP}(Problem 1.8.3.1)
Definition : A sequence whose terms are
reciprocals of terms of an AP is called ‘Harmonic progression’
and is denoted by ‘{HP}’
We have seen that the general term Tn
of an {AP} is a+(n-1)d and hence general term Tn
of a {HP} is ![]() ( Reciprocal of nth term of an AP)
( Reciprocal of nth term of an AP)
{HP}= {![]() ,
, ![]() ,
, ![]() ,
, ![]() …….
……. ![]() }
}
Note: There is no formula to find Sn of a HP.
For easy understanding we can say {HP} = {1/AP}.
In order to solve a problem on HP, we could take reciprocal of terms of given
HP and then solve the problem as if it is a problem on AP.
1.8.6
Problem 1 : In a
HP T4= ![]() and T10=
and T10= ![]() find T19.
find T19.
Solution:
In a HP Tn= ![]()
![]() T4=
T4= ![]() =
= ![]() (given)
(given)
![]() T4=
T4=
![]() =
= ![]()
![]() a+3d =12 ==========à(1)
a+3d =12 ==========à(1)
T10= ![]() =
= ![]() (given)
(given)
![]() a+9d =42 ==========à (2)
a+9d =42 ==========à (2)
Subtract (1) from (2) we get
a+9d-(a+3d) =42-12
![]() 6d = 30
6d = 30
![]() d =5
d =5
Substitute 5 for d in (1) we get
a+3*5 =12
a = (12-15) = -3
Substitute values for a and d in T19 we get
T19= ![]()
= ![]()
= ![]()
1.8.7 Arithmetic, Geometric and
Harmonic means (AM,GM and HM)
Definition : if {a, A and b }are in AP then A is called ‘Arithmetic Mean
(AM)’ between a and b and is denoted by ‘A’
The derivation for A is shown below.
Since a, A and b are in AP, by definition we have
A-a =b-A( ![]() difference between a term and its preceding term is a
constant in an AP)
difference between a term and its preceding term is a
constant in an AP)
2A = a+b
A = ![]()
Definition : if {a, G and b }are in GP then G is called ‘Geometric Mean (GM)’ between a and b and is
denoted by ‘G’
The derivation for G is shown below.
Since a, G and b are in GP, by definition we have
![]() =
=![]() (
( ![]() the ratio of a term to
its preceding term is constant in a GP)
the ratio of a term to
its preceding term is constant in a GP)
G2= ab
G = ![]()
Definition : if {a, H and b }are in HP then H is called ‘Harmonic Mean (HM)’ between a
and b and is denoted by ‘H’
The derivation for H is shown below.
Since a, H and b are in HP, by definition we have
(![]() ,
,![]() ,
,![]() ) are in AP
) are in AP
Thus ![]() -
-![]() =
= ![]() -
-![]() (
( ![]() difference between a term and its preceding term is constant in an AP)
difference between a term and its preceding term is constant in an AP)
![]() =
= ![]() +
+![]()
= ![]()
![]() 2ab =H(a+b)
2ab =H(a+b)
![]() H =
H = ![]()
1.8.7 Theorem: If A, G and H are AM, GM and HM
of 2 positive numbers respectively, then prove that A,G and H are in GP
We need to prove that G/A =H/G (i.e. the ratio of term to
its preceding term is constant)
We are given:
A = ![]()
G = ![]()
H = ![]()
A*H = ![]() *
*![]() = ab= (
= ab= (![]() )2= G2
)2= G2
Or ![]() = G/A : This proves that A,G and H are in GP
= G/A : This proves that A,G and H are in GP
Observations : We
notice that A![]() G
G![]() H for two positive numbers
H for two positive numbers
1.8 Summary of learning
|
No |
Points to remember |
|
1 |
{AP}=
{a, a+d, a+2d,a+3d …..a+(n-1)d} General term of an AP
is Tn= a+(n-1)d |
|
2 |
|
|
3 |
Sn of an AP = n*[2a+(n-1)*d]/2= n*(a+ Tn)/2 |
|
4 |
{GP} =
{a, ar, ar2, ar3 ……….. ar(n-1)}
Tn= Tn-1*r = ar(n-1) |
|
5 |
Sn of a GP = a(1- rn)/(1-r) If r<1 then Sinfinity
= a/(1-r) |
|
6 |
{HP}= { |
|
7 |
Arithmetic
Mean(AM): A= |
|
8 |
Geometric
Mean (GM): G = |
|
9 |
Harmonic Mean (HM): H = |
Additional Points:
1.8.8 Mathematical Induction:
In 1.8.4, we have arrived at the formula for the series
1+2+3…+n as
Sn= ![]()
We shall prove the same by principle of mathematical
induction:
Mathematical Induction states that :
If f(n) is a statement such that f(n) is true for n=1,
then we prove the statement for n=n+1 after assuming it to be true for n.
Note that by using this method, we cannot arrive
at a formula/statement which is true for all values of n, however given the formula/statement,
We can prove them.
Example
: Prove that
1+2+3 ….+n = ![]() by mathematical
induction.
by mathematical
induction.
Proof :
Let the statement be f(n) = (1+2+3 ….+n)
We notice that f(1) = 1
And we also notice that 1(1+1)/2=1. Hence f(1) is true
Let the given statement be true for n
i.e. 1+2+3 …+n = ![]()
Let us now prove that statement is also true for n+1.
Add the next term, (n+1) to both sides of the above
statement.
![]() 1+2+3 ….+n +(n+1) =
1+2+3 ….+n +(n+1) = ![]() +(n+1)
+(n+1)
= (n+1)(n/2+1) =
(n+1)(n+2)/2 which is again of the
form m(m+1)/2, where m = n+1.
This proves that the given statement is true.
1.8.8
Problem 1: 1*3 +
3*5 + 5*7 +…….+ (2n-1)*(2n+1) = n(4n2+6n-1)/3
Proof :
Let the statement be f(n) = 1*3 + 3*5 + 5*7 +…….+
(2n-1)*(2n+1)
We notice that f(1) = 1*3
And we also notice that 1(4*12+6*1-1)/3 = 3
Hence f(1) is true.
Let the given statement be true for n
i.e. 1*3 + 3*5 + 5*7 +…….+ (2n-1)*(2n+1) = n(4n2+6n-1)/3
Let us now prove that statement is also true for n+1.
Add the next term (2(n+1)-1)* (2(n+1)+1) = (2n+1)*(2n+3)
to both sides of the above statement.
![]() 1*3 + 3*5 + 5*7 +…….+
(2n-1)*(2n+1) + (2n+1)*(2n+3) = n(4n2+6n-1)/3
+(2n+1)*(2n+3)
1*3 + 3*5 + 5*7 +…….+
(2n-1)*(2n+1) + (2n+1)*(2n+3) = n(4n2+6n-1)/3
+(2n+1)*(2n+3)
= (n+1)(n/2+1) =
(n+1)(n+2)/2 {After simplification: verify yourself}
which is again of the form
m(m+1)/2 where m = n+1.
This proves that the given statement is true.
Exercises: Using mathematical induction to prove
the following:
1. ![]() n2 =
n(n+1)(2n+1)/6
n2 =
n(n+1)(2n+1)/6
2. ![]() n3 = n2(n+1)2/4
= (
n3 = n2(n+1)2/4
= (![]() )2
)2
3. 1+3+5 . . . . +(2n-1) = n2 ( Note that this is an AP also)