5.4. Dispersion (Deviation) of data:

 

5.4.1 Mean, Median, Mode for grouped data

 

Sometimes when the scores are large it becomes difficult to calculate Mean, Median and Modes. When scores are large we use class intervals to represent data as studied in the 5.1.1. Example 2. When scores are represented in class intervals we follow a slightly different method for the calculation of Mean, Median and Modes. Let us study the method using an example.

 

5.4.1. Example 1:  Assume that the following data about the presence of 110 people from different age groups in a marriage function is collected.

 

Working:

 

Class Interval      (CI) (Age groups)	Frequency (f)
0-10	7
10-20	13
20-30	24
30-40	26
40-50	18
50-60	12
60-70	10

 

Note:  In the above distribution, we notice, that in each CI, upper limit of a class interval appears again as a lower limit in the next class interval (for example 10 appears twice, once in CI: (0-10) and in CI:(10-20)).

 

Thus the question arises where should the score for upper limit (10) be included? However, by convention the upper limit is not included in the corresponding class interval and is included in the next class interval.

(i.e. the score 10 is included in CI: 10-20 and not in CI: 0-10)

Let us calculate the mean, median and mode for grouped data.

To recollect, if we had ungrouped scores then

Mean = ()/Number of scores

Similarly Median would be in the interval ‘30-40’ (which has 55^th and 56^th occurrence of the score).

Since we do not have individual scores, it will not be possible for us to arrive at the exact mode and exact median easily. In such cases we follow a different method:

 

We use the following notations to arrive at values as shown below

 

N = Total number of scores = 110

‘Mid point’( Or ‘Class mark’)(x) =  

f= frequency

f(x) = f*x

‘Cumulative frequency’ of a class interval is sum of all the frequencies of all the class intervals up to this class interval.

 

C-I	Frequency (f)	Cumulative frequency(cf)	Mid Point (x) of CI	f(x) =f*x
0-10	7	7	5	35
10-20	13	20=7+13	15	195
20-30	24	44=20+24	25	600
30-40	26	70=44+26	35	910
40-50	18	88=70+18	45	810
50-60	12	100=88+12	55	660
60-70	10	110=100+10	65	650
Total	N=110			= 3860

 

By definition Mean =  =  = 35.09  35.1

Since number of score is 110, Median must be between 55^th and 56^th score which is in the class interval ‘30-40’.(because up to the class interval 20-30 we have 44 (cf) scores and up to the class interval 30-40 we have 70 scores (cf)).

Let

i= size of the class interval = 11(There are 11 scores in each class interval)

L= Lower limit of the class interval which includes the median score (This CI (’30-40’) is also called Median class interval) = 30 ??

F =Cumulative frequency up to the median class interval = 44

m = frequency of the median class interval = 26

Then

Median = L+ ()*i

= 30+ (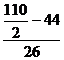)*11 = 30+*11 = 30+4.65 = 34.65

 

Mode lies in the class interval ‘30-40’ and the formula for mode is

Mode = 3*median-2mean

                      = 3*34.65- 2*35.1

                      = 33.75

 

5.4.2 Measures of dispersion: Range, Deviations

 

Let us take the following example of attendance of a class for 2 different weeks in a month.

First week    : 45,44,41,10,40,60 : Mean (average) = 40

Second week:  35,45,40,45,40,35:  Mean (average) = 40

 

In both the cases, the average attendance is 40. But we also observe the following:

 

1. First week has registered a very low attendance of 10 and a high attendance of 60, with maximum deviations (dispersions) from average where as

2. In the second week, the deviations from average are not high. In simple terms we can say that attendance is consistent in the second week.

Thus we conclude that, average may not give a correct picture.

Therefore we need other measures to arrive at meaningful conclusions.

We introduce the following concepts:

The difference between two extreme scores of a distribution is called the ‘Range’

Range = Highest Score- Lowest Score= H-L

Co-efficient of Range =  =

We have learnt that, median is a score that divides the distribution of score in to two equal parts. Similarly we define Quartile as the distribution of scores in to four equal parts. In such cases the distribution is divided in to four parts as:

1st Quartile (Q₁), 2nd Quartile (Q₂), 3rd Quartile (Q₃). They are scores at 1/4th, 1/2nd and 3/4th the distribution of scores.

We note that 2nd Quartile is the Median itself.

Quartile deviation( Semi interquartile-range) is calculated as

QD = (Q₃-Q₁)/2

 

5.4.2 Example 1 : Calculate Range, Co-efficient of Range ,Quartile deviation  and Co –efficient of Quartile deviation for the scores 16,40,23,25,29,24,20,30,32,34,43

 

Working:

 

By arranging the scores in ascending order, we get

16,20,23,25,29,30,32,34,40,43.

Note that L= 16, H =43 and N=11

Therefore 

Range = H-L = 43-16 = 27

 

Co-efficient of Range ===0.46

Since there are 11elements

-for Q₁ the score to be considered is 3^rd (1/4^th of 11) score = 23.

-for Q₃ the score to be considered is 8^th (3/4^th of 11) score = 34

QD = (Q₃-Q₁)/2

 = = 5.5

Co-efficient of QD = (Q₃-Q₁)/ (Q₃+Q₁) = ==0.1

For grouped data, we have seen earlier that

If N = Total number of scores,

i = Size of the class interval,

L = Lower limit of the Median class interval,

F = Cumulative frequency (cf) up to the median class interval and

f = frequency of the median class interval

Then

Median = L+ (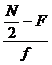)*i = Q₂

Similarly for grouped data we calculate

Q₁ = L+ (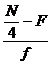)*i

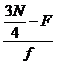Q₃ = L+ ()*i

Where

L = Lower limit of the respective Quartile class interval

F = Cumulative frequency (cf) up to the respective Quartile class interval

f = frequency of the respective Quartile class interval

 

5.4.2 Example 2: Calculate Range, Co-efficient of Range, Quartile deviation and Co –efficient of Quartile deviation for the grouped data of 100 scores

 

CI	f
4-8	6
9-13	10
14-18	18
19-23	20
24-28	15
29-33	15
34-38	9
39-43	7

 

Working:

 

Here we have N = 100, i = 5 and let us calculate cumulative frequency as follows:

 

CI	f	cf
4-8	6	6
9-13	10	16
14-18	18	34
19-23	20	54
24-28	15	69
29-33	15	84
34-38	9	93
39-43	7	100

 

For Q₁ we need to find 25^th (1/4^th of 100) element which lies in the class interval ’14-18’

L= 13.5, F=16, f= 18

Q₁ = L+ (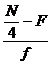) * i

= 14 +*5 = 14 + 2.5 = 16.5

For Q₃ we need to find 75^th (3/4^th of 100) element which lies in the class interval ’29-33’

L = 29, F = 69, f = 15

Q₃ = L+ (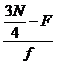)*i

=29+*5 = 29+2 =31

QD = (Q₃-Q₁)/2

= =7.25

Co-efficient of QD = (Q₃-Q₁)/ (Q₃+Q₁) = ==0.31

 

5.4. 3 Mean Deviation for Ungrouped data:

 

As the name suggests, here we calculate the average deviation from the mean.

 

Note: Mean Deviation can be found in two ways - using Median method or using Mean method.

 

5.4.3 Example 1.  Calculate the mean deviation for the scores given below, by BOTH methods.

90,125,115,100,110.

 

Working:

 

By rearranging the scores in increasing order we get

90,100,110,115,125

Here we have N= 5, = 90+100+110+115+125=540

 The median (M) = 110 (3rd term)

The mean () of scores

is =  = =108

 

Scores(X)	I Method Deviation from Median D= X-M	II Method Deviation from Mean D= -M
90	-20(90-110)	-18(90-108)
100	-10(100-110)	-8(100-108)
110	0(110-110)	2(110-108)
115	5(115-110)	7(115-108)
125	15(125-110)	17(125-108)
= 540	=20+10+0+5+15= 50	=18+8+2+7+17= 52

In the above calculation |D| is the absolute value of D (we consider value of D as always positive).

By Median method, Mean deviation =  = =10

By Mean method, Mean deviation =  = =10.4

 

5.4.4 Mean Deviation for Grouped data:

 

Note: As in the case of ungrouped data, Mean Deviation can be found in two ways (Using Median method and Mean method)

 

5.4.4 Example 1. Compute Mean Deviation of

 

C.I	f
0-20	8
20-40	10
40-60	19
60-80	14
80-100	9

 

Workings:

 

Here we have N = 60 and i= 21

Median (M) = L+ ()*i

= 40 +*21 = 40+13.3 = 53.3 (Use the values from the table arrived below)

Mean () =  = = 52 (Use the values from the table arrived below)

 

C.I	Mid Point (x)	f	I Method Deviation from Median			II Method Deviation from Mean
			cf	D = x-M	f*|D|	fx	D = x-	f*|D|
0-20	10	8	8	-43.3	346.4	80	-42	336
20-40	30	10	18	-23.3	233	300	-22	220
40-60	50	19	37	-3.3	62.7	950	-2	38
60-80	70	14	51	16.7	233.8	980	18	252
80-100	90	9	60	36.7	330.3	810	38	342
		N=60			=1206.2	=3120		= 1188

 

By Median method, Mean Deviation =  == 20.10

By Mean method, Mean Deviation =  == 19.8

 

5.4.5. Graphical representation of frequency distribution

 

In earlier sessions we have seen that, graphical representation of data is always easy to understand and interpret. Two important types of representations are histogram and frequency polygon.

 

Histogram: Here we represent the distribution in vertical rectangles. The rectangles are drawn side by side. The vertical height is proportional to the frequency and is represented on y axis. The class intervals are represented on x-axis .

We need a graph sheet for this type of representation. Class intervals (CI) are marked as the base of rectangle on x axis. Frequencies are marked as the height of rectangle on y axis.

 

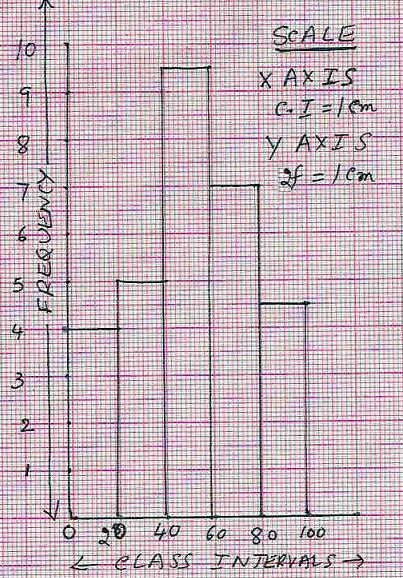
5.4.5 Example 1. Draw histogram and frequency polygon for

 

C.I	f
0-20	8
20-40	10
40-60	19
60-80	14
80-100	9

 

Working:

Use a suitable scale for representing Class interval and frequency

(In this case let 1C.I = 1cm and 2f=1cm)

 

Histogram:

 

Step 1: Take a graph sheet. Mark 0 and draw x –axis and y-axis.   Step 2: On the x-axis mark the class intervals adjacent to each other from 0.  Use 1cm as the width of each class interval. (Thus the scale for C.I. is 1C.I. = 1cm)   Step 3: Convert frequency to a suitable unit so that the graph fits into one page easily. In this example use the scale 1cm = 2f. Therefore we have:           8f =4cm, 10f =5cm, 19f = 9.5cm, 14f = 7cm and 9f =4.5cm. (Thus the scale for frequency is 2f = 1cm)       C.I f X(base) Y(height) 0-20 8 0 to 1 cm 4cm 20-40 10 1 to 2 cm 5cm 40-60 19 2 to 3 cm 9.5cm 60-80 14 3 to 4 cm 7cm 80-100 9 4 to 5 cm 4.5cm         Step 4: Draw a rectangle of height 4cm representing the first CI (0-20)       Step 5:  Draw a rectangle of height 5cm representing the next CI 20-40, next to the previous one, so that these two vertical bars have a common side. Draw the remaining rectangles for other class intervals.

 

Observations:

1.Class intervals are represented on x axis and frequency on y axis

2.The scales chosen for both the axes need not be same.

3. Since the sizes of class intervals are same, width of the rectangles are also same.

4. Since there are no gaps in the class intervals the rectangles are contiguous (No space in between them).

5. Height of the rectangle is proportional to the respective frequencies of the C.I.

Note : If there are breaks in the class intervals(usually in the beginning)  a zig-zag curve (is drawn between the  class intervals).

 

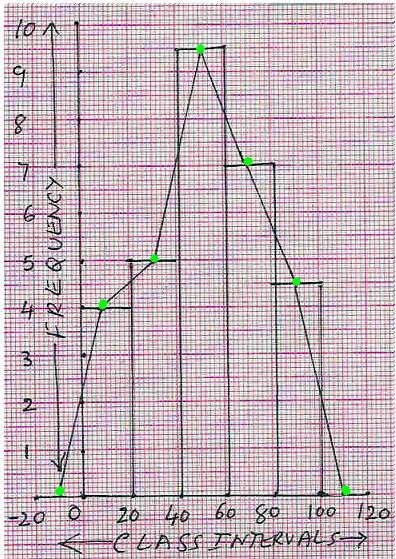
Frequency Polygon (Method I):

When the mid points of the adjacent tops of the rectangles are joined by straight lines, the figure so

obtained is called ‘frequency polygon’

 

Step 1:  Draw the histogram as above.   Step 2: Mark non existing class interval (since f = 0, height = 0cm) one each at two extreme ends (i.e. (-20) - 0 on the left side and 100 -120 on the right side).     Step 3:  Identify middle point for each of the class interval bars (at -0.5, 0.5, 1.5, 2.5, 3.5, 4.5 and 5.5cms on x-axis and y being (0, 4, 5, 9.5, 7,4.5  and 0 ) respectively).        C.I f x(Mid of base) y (x,y) (-20) -0 0 -0.5 0 (-0.5 ,0) 0-20 8 0.5 4 (0.5,4) 20-40 10 1.5 5 (1.5,5) 40-60 19 2 .5 9.5 (2.5,9.5) 60-80 14 3.5 7 (3.5,7) 80-100 9 4.5 4.5 (4.5,4.5) 100-120 0 5.5 0 (5.5,0)       Step 4:  Join two consecutive mid points of bars by a straight line to get the required polygon

 

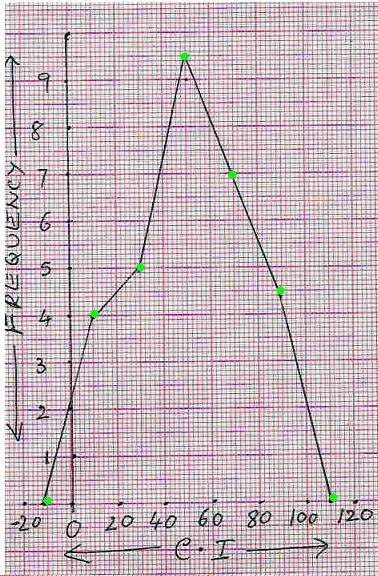
Frequency Polygon (Method II):

 

Step 1: Mark non existing class intervals one each at two extreme ends (i.e. (-20) - 0 on the left side and 100 - 120 on the right side).   C.I f x(Mid of base) y (x,y) -20 -0 0 -0.5 0 (0,0) 0-20 8 0.5 4 (.5,4) 20-40 10 1.5 5 (1.5,5) 40-60 19 2 .5 9.5 (2.5,9.5) 60-80 14 3.5 7 (3.5,7) 80-100 9 4.5 4.5 (4.5,4.5) 100-120 0 5.5 0 (5.5,0)       Step 2:  Identify middle point for each of the class intervals as per the scale used (in this example 1C.I. = 1cm). These points are -0.5, 0.5, 1.5, 2.5, 3.5, 4.5 and 5.5 on the x-axis.     Step 3:  Identify the height of frequency for each class interval as per the scale used (2f=1cm).   These points are 0, 4, 5, 9.5, 7,4.5  and 0  on the y-axis.   Step 4: Plot and join these points.

 

Note : If the  mid points  of class intervals are very close,  then we get a frequency curve by joining these points by a smooth curve rather than  joining by straight lines.

 

 

 

5.4 Summary of learning

 

 

No	Points to remember
1	Mean = (For grouped data)
2	Median = L+ ()*i(For grouped data)
3	Mode = 3*median-2mean(For grouped data)
4	Co-efficient of Range = (For ungrouped data)
5	Mean deviation = (For ungrouped data)
6	Mean Deviation = (For grouped data)

 

 

Additional Points:

 

5.4.1 Assumed mean method for calculation of mean for grouped data

This method is very useful when class intervals and their frequencies are very large. In this method we assume one of the mid-points to be the mean and find the deviation from that mid-point and hence this method is called  ‘assumed mean method’.

Let us take the example solved earlier (5.4.1 Example 1) to illustrate this method.

 

Let  25  be the assumed mean (any score can be assumed to be the mean but we normally take the score which is in the middle part of the distribution as assumed mean)

The Deviation D (D = Score- Assumed mean) is calculated for each of the score.

Then Average (mean) = A + ()/Number of scores

 

C-I	Frequency (f)	Mid Point (x) of CI	Deviation D= A-M	fD= f*D
0-10	7	5	-20(=5-25)	-140
10-20	13	15	-10(=15-25)	-130
20-30	24	25= A	0	0
30-40	26	35	10(=35-25)	260
40-50	18	45	20(=45-25)	360
50-60	12	55	30(=55-25)	360
60-70	10	65	40(=65-25)	400
Total	N=110			=1110

 

Average (mean) = A + ()/Number of scores = 25+1110/110 = 25+10 = 35

 

This is the same value(approximate) which we got earlier.

 

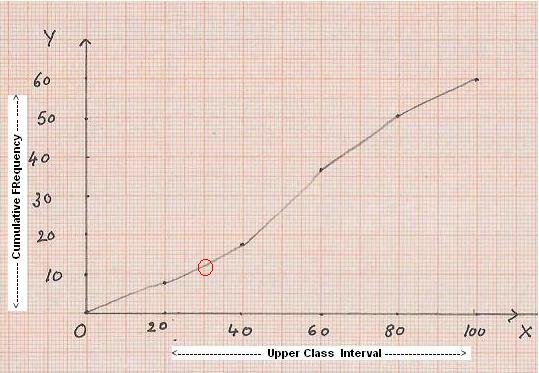
5.4.5 Cumulative Frequency Curve (Ogive):

In this type of graph we plot the points corresponding to cumulative frequency for the given data (Ungrouped or grouped) and join the points by a smooth curve.

 

The given data (actual score or Upper class limit in case of grouped data) is marked along the x-axis. Cumulative frequency is marked along the y-axis.

 

Let us again consider   the same example we have taken in 5.4.5 Example 1.

 

5.4.5 Example 2. Draw Ogive for

 

C.I	f
0-20	8
20-40	10
40-60	19
60-80	14
80-100	9

 

Working:

1. First arrive at an ‘imaginary’ class interval with 0 frequency (In this case -20 to 0). 2. Prepare the cumulative frequency table as shown below starting with the imaginary class interval (-20 to 0).               C.I f cf Point(x,y)  -20-0 0 0 (0,0)     0-20 8 8 (20,8)   20-40 10 18 (40,18)   40-60 19 37 (60,37   60-80 14 51 (80,51)   80-100 9 60 (100,60     3. Use a suitable scale for x-axis for representing the upper Class limit (In this case let 1cm=10 upper class limit). 4. Use a suitable scale for y-axis for representing the cumulative frequency (In this case let 1cm =10cf) 5. Plot the points corresponding to each upper class limit as shown in the     adjacent graph. 6. Join these points by a smooth curve (This curve is Ogive).

 

From the cumulative frequency curve it will be easy to arrive at frequencies for different class intervals.

(For example: From the above graph we can conclude that the cumulative frequency for scores up to 30 is 13. This point is circled red in the graph).