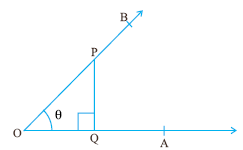
8.4: Trigonometric Identities:

 

8.4.1 Fundamental identities:

We have learnt in Section 8.1 the ratios for sin, cos and tan of angles.

 

sin	Perpendicular/Hypotenuse	PQ/OP
cos	Base/Hypotenuse	OQ/OP
tan	Perpendicular/Base	PQ/OQ
By Pythagoras theorem we know that PQ2 + OQ2 = OP2   -----à(1)  PQ2/OP2 + OQ2/OP2 = 1(By dividing both sides of equation (1) by OP2) (PQ/OP)2 + (OQ/OP)2 = 1 (sin)2 + (cos)2 = 1 sin2 + cos2 = 1    ----------(I) By dividing both sides of equation (1) by OQ2 we get PQ2/OQ2 + 1 = OP2/OQ2 (PQ/OQ)2 + 1 = (OP/OQ)2 1 + (tan)2 = (sec)2                                         tan2 + 1 = sec2      ----------(II) By dividing both sides of equation (1) by PQ2 we get 1 +OQ2/PQ2 = OP2/PQ2  1 + (OQ/PQ)2 = (OP/PQ)2 1 + (cot)2 = (cosec)2                             1 + cot2 = cosec2    ---------(III) The equations (I), (II) and (III) are called ‘Fundamental identities’. From Fundamental identities we can also arrive at the following: Since sin2+cos2=1 sin2= 1-cos2  sin = (1-cos2) Since sin is positive when  is acute, sin = +(1-cos2) Similarly we can arrive at cos = +(1-sin2) From the other two fundamental identities we can arrive at the following: tan = +(sec2-1), sec = +(1+tan2), cot = +(cosec2-1), cosec = +(1+cot2) tan = sin/ cos = sin/ +(1-sin2)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

In summary we have the following relationships between various standard trigonometric ratios.

Note: All these relationships can be derived by using just sin²+cos²=1.

 

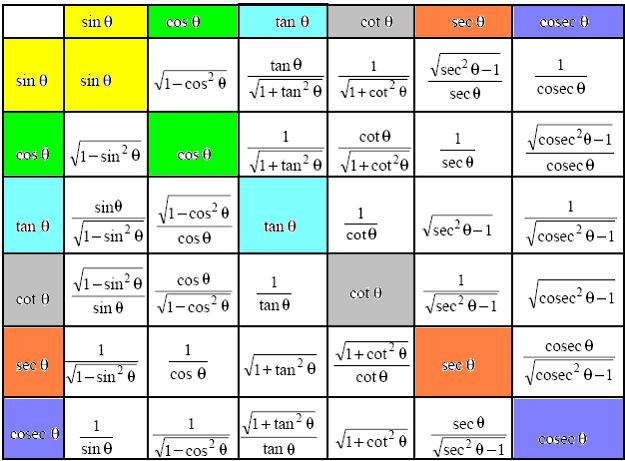
The Fundamental identities are useful for simplifying various trigonometric expressions.

 

8.4 Problem 1: If  (1+x²)*sin = x prove that sin²/ cos² + cos²/ sin² = x² + 1/x²

 

Solution:

It is given that

 (1+x²)*sin = x

 sin = x/ (1+x²)

 sin² = x²/(1+x²) (By squaring both sides)--------(1)

But sin²+cos²=1 (Fundamental identity)

 cos² = 1 - sin² (By transposition)

= 1 - x²/(1+x²) (By substitution)

= (1+x² - x²)/(1+x²)

= 1/(1+x²)                            ----------(2)

From (1) and (2)

sin²/cos² =

{x²/(1+x²)}/{1/(1+x²)} = x²  -----------(3)

Similarly, cos²/sin² = 1/x²           -----------(4)

From (3) and (4)

sin²/cos² + cos²/sin² = x² + 1/x²

 

8.4 Problem 2: prove that sin⁶+cos⁶=1-3*sin².cos²

 

Solution:

Let x = sin² and y = cos²

Since sin²+cos²=1. It follows that x+y = 1

Note LHS of the given equation is of the form x³+y³

We also know the identity x³+y³ = (x+y)³-3xy(x+y) = 1-3xy(x+y =1)

= 1 – 3*sin².cos²( By substituting values for x and y)

 

8.4 Problem 3: Prove that tanA/(secA-1)+tanA/(secA+1) = 2cosecA

 

Solution:

LHS = {tanA(secA+1+secA-1)}(sec²A-1) (By taking out tanA as common factor and having (secA+1)*(secA-1) as common denominator)

= 2tanA.secA/tan²A (sec²-1 = tan²)

= 2secA/tanA (canceling of tanA)

= 2secA*cosA/sinA (tanA = sinA/cosA)

= 2/sinA (cosA = 1/secA)

= 2cosecA

 

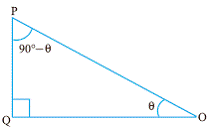
8.4.2 Trigonometric ratios of complimentary angles:

In a right angled triangle, if  is one angle then the other angle has to be 90⁰-(sum of all angles in a triangle is 180⁰).

 

In the adjacent figure, QOP =  hence QPO = 900- If we consider QOP then sin = PQ/OP    ----à(1) cos = OQ/OP   ----à(2) tan = PQ/OQ   ----à(3) If we consider QPO then cos(900-) = PQ/OP    --à (4) sin(900-) = OQ/OP    ---à(5) cot(900-) = PQ/OQ  ---à(6) By comparing (1), (2) and (3) with (4), (5) and (6) respectively and then by comparing their inverses, we note that        1 sin = cos(900-) 2 cos = sin(900-) 3 tan= cot(900-) 4 cosec = sec(900-) 5 sec = cosec(900-) 6 cot= tan(900-)

 

8.4 Problem 4: Evaluate 3sin62⁰/cos28⁰ - sec42⁰/cosec48⁰

 

Solution:

Note that 28 = 90-62 and 48 = 90-42

cos(28) = cos(90-62) = sin62

cosec(48) = cosec(90-42) = sec(42)

3sin62⁰/cos28⁰ - sec42⁰/cosec48⁰

= 3sin62⁰/sin62⁰ - sec42⁰/sec42⁰

= 3-1 = 2

 

 

8.4. Summary of learning

 

 

No	Points studied
1	sin2+cos2=1,tan2 + 1 = sec2,1 + cot2 = cosec2
2	Trigonometric ratios of complimentary angles