2.3. Logarithms:

 

In 2.2 we learnt exponents and several laws.

To recollect, some numbers can be represented as:

Base ^Exponent = Number

This method of representation is called ‘exponential form’.

Ex: 2³ = 8

 

This relationship can be represented in a different format:

log _base Number = Exponent

EX : log₂ 8 = 3 ( Equivalent to saying  8 = 2³)

 

The ‘logarithm’ (log) of any number to a given base is the value of the index to which the base must be raised to get the given number

The above method of representation is called ‘logarithmic form’.

 

We have seen that

1) x⁰ =1

Hence log_x1 = 0

2) x¹ =x

Hence log_xx = 1

 

From laws of exponents we can derive the following laws of logarithms:

1. Product law:  log_a(mn) = log_a m+ log_a n (By  x^m.xⁿ= x^m+n property)

2. Quotient law: log_a(m/n) = log_a m - log_a n(By  x^m/xⁿ= x^m-n property)

3. Power law:    log_amⁿ = nlog_a m(By  (x^m)ⁿ= x^mn property)

4. log_am^1/n  = (1/n) log_am ( By Power law)

 

2.3 Problem 1: Find x if log₉ 243=x

 

Solution:

This is equivalent to saying 9^x= 243 = 3*3*3*3*3 = 3⁵

But 9^x=3^2x

3^2x= 3⁵

 2x =5

 x =5/2

 

 

Logarithms to the base 10 are called ‘common logarithms’

Convention: If base is not given, then the base is assumed to be 10 (log20 implies log₁₀20).

We have seen that log1=0 and log10=1.

 

2.3 Problem 2: Given log x = m+n and log y = m-n. Express log (10x/y²) in terms of m and n.

 

Solution:

log (10x/y²) = log 10x – log y² (quotient law)

= log 10 + log x – 2 log y( product law, power law)

= 1 + (m+n) – 2(m-n) (substitution, log 10 = 1)

= 1-m+3n

 

2.3 Problem 3: Given 2log x+1 = log 250 find x, log 2x

 

Solution:

Since base is not given, it is assumed to be 10.

log 250  = log (10*25) = log 10 + log 25 = 1 + log 25 (log 10 = 1)

  2log x + 1 = 1 + log 25

i.e.  2log x = log 25

But 2log x =   log x²(Power law)

 log x²  = log 25

 x²=25

i.e. x=5

 log 2x = log 10 = 1

 

2.3 Problem 4: If 2log y – log x – 3 = 0 express x in terms of y

 

Solution:

Since 2log y – log x – 3 = 0

log x = 2log y - 3  = 2log y – 3log 10

= log y²- log 10³ = log (y²/10³)

Thus

log x = log (y²/10³)

 x = y²/10³ = y²/1000

 

2.3 Problem 5: If log 2 = 0.3010 and log 3 = 0.4771 find value of log

 

Solution:

 = = (30/4)^1/2

 log  = (1/2)log(30/4) = 1/2(log30-log4)

= ½(log 10 + log 3 - 2log 2)

= ½(1+0.4771-0.6020)

=½(0.8751)

= 0.43755

 

We have seen that log 1 = 0, log 10 = 1(log_x x = 1 and log_x 1 = 0)

Thus log x for any value of x (1 x 10) has to be in between 0 and 1.

In fact log 2 = 0.3010 and log 3 = 0.4771 (We get these values from log tables discussed later)

 

Also note

log 100 = log(10*10)=log10+log10=2log10=2

log 1000 = log(10³) = 3log10=3*1=3 and so on….

 

log value of a number has two parts: an integer part and decimal part.

The integral part of the logarithm is called ‘characteristic’ and the decimal part of the logarithm is called ‘mantissa’.

In case of log 2 = 0.3010, 0 is characteristic and .3010 is mantissa.

 

We use a table called ‘logarithmic table’ to find the values of numbers to the base 10.

A section of the table is given below:

As we observe from adjacent figure, the table has three parts. 1. First part is the left most column (Blue box) which contains  numbers from 1.0 to 1.5(The adjacent figure only has a part of the table from 1.0 to 1.5 but the full table has values from 1.0 to  9.9). 2. Second part contains 10 columns (red box) 3. Third part contains 9 columns (pink box) (with Mean differences as the heading) Against each number in the first column there are 10 columns  in 2nd part, having decimal values corresponding to digits from 0 to 9. Against each number in the first column there are 9 columns in 3rd part, having decimal values corresponding to digits from 1 to 9.

If we look at the full logarithmic table we  notice the values are from 0.0000 to 1.0 (0.9996+.0004) The table represents values from 0 to 1 correspondingly from log1 to log10 (log 1 = 0, log 10 = 1)

 

Observe the following:

 

Number	=(Equivalent)	log  of number	=	=(Expansion)	=(Simplification)
3257 =	3.257*103	log(3257) =	Log(3.257*103)	= 3log10 +log(3.257)	= 3+ log(3.257)
325.7 =	3.257*102	log(325.7) =	Log(3.257*102)	= 2log10 +log(3.257)	= 2+ log(3.257)
32.57 =	3.257*101	log(32.57) =	Log(3.257*101)	= 1log10 +log(3.257)	= 1+ log(3.257)
3.257=	3.257	log(3.257)=	Log(3.257)	= 0log10 + log(3.257)	=      log(3.257)
0.3257 =	3.257*10-1	log(0.3257) =	Log(3.257*10-1)	= -1log10 +log(3.257)	=  +log(3.257)
0.03257 =	3.257*10-2	log(0.03257) =	Log(3.257*10-2)	= -2log10+log(3.257)	=  +log(3.257)
0.003257 =	3.257*10-3	log(0.003257) =	Log(3.257*10-3)	= -3log10+log(3.257)	=  +log(3.257)
0.0003257 =	3.257*10-4	log(0.0003257) =	Log(3.257*10-4)	= -4log10+log(3.257)	=  +log(3.257)

Note: –log10 is not written as –1 but as

Thus if we know the logarithmic value of a number having one integer digit, then by using product and power laws of logarithm we can find the values of any given number which is  multiple of the given number.

 

Note that the logarithmic table given in the adjacent figure

is for values from log 1.0 to log(3.5) 

(Note: log 1 = 0)

 

How to use the log table?

Let us find the value of log 32.57   1)First convert the given number into a decimal such that there is only one digit in the integer part and there are not more than three digits in the decimal part.   Thus 32.57 = 3.257*101log(32.57) = 1+ log(3.257)   2)Split the given four digit number into 3 parts (first part with two digits, then two parts of one digit each).In this example 32.57 is split into three parts (3.2, 5 and 7).   3)Identify the row corresponding to first part of 2 numbers (In this example 3.2).   4)In this row find the value under the number which corresponds to the second part(in this example under 5). The value is 0.5119   5)To the above value, add the value under  the number which corresponds to the third part (in this example under 7). The value is 0.0009     6)Sum of values of steps 4 and 5 is the log value of 1/10th of the given number(32.57)(0.5128 = 0.5119 + 0.0009) is the log value of 3.257   log(32.57) = 1+ log(3.257) = 1+0.5128   Similarly log (2.223) = 0.3464+0.006 = 0.3470 and hence log(22.23) = 1.3470, log(222.3) = 2.3470,……

2.3 Problem 6: Find a, b and c If log(a) = 1.7782, log(b)= .7782 and log(c)=1.5564 and log6=0.7782

 

Solution:

Log(a)=1.7782  = 1+0.7782 = log10+log6 = log60

a=60

log(b)= .7782 = log(10^-2)+0.7782 = log10^-2+log6 = log(6/100)

b=0.06

log(c)=1.5564 = 2 (0.7782) {By intuition} = 2 log6  = log 6²

c=6²=36

 

If log3257 = 3.5128, then 3257 is called ‘antilogarithm’ of 3.5128 and we write antilog3.5128 = 3257 or log^-1 (3.5128) = 3257.

Like logarithmic tables we also have antilog tables, a section of which is given below. The usage of antilog table is similar to log table.

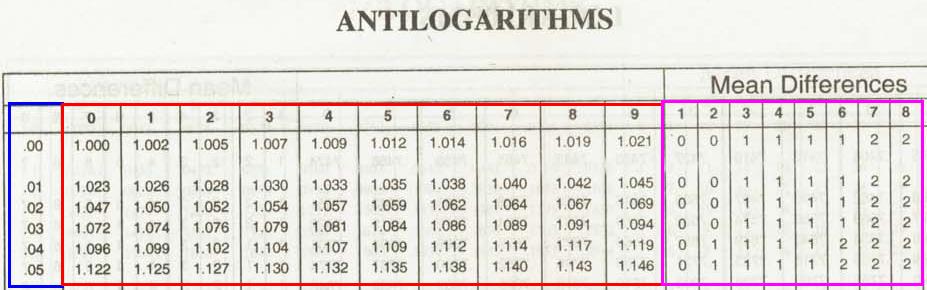
If log table has values corresponding to 1.00 – 9.9, antilog table has values corresponding to 0.00 to .99

 

Change of base of logarithm:

log_x y= log_x a/ log_y a

 

Proof:

Let log_x a = p,

x^p=a   ----à(1)

 Let log_y a=q

 y^q=a  ----à(2)

log_x y = r

And Let log_x y =r

 x^r=y    ----à(3)

From (2) a = y^q  ( by substituting from (3) for y) we get

a=( x^r)^q= x^rq (By law of exponents)

 

But from (1) a = x^p

Hence x^p= x^rq

 p = qr

By substituting values for p, q and r.

log_x a = log_y a * log_x y

i.e. log_x y = log_x a/ log_y a

 

Similarly we can prove that

log_x y = log_a y/ log_a x

 

2.3 Problem 7: If x = 1+log_abc, y= 1+log_bca , z = 1+log_cab, show that xy+yz+zx= xyz

 

Solution:

Since x = 1+log_abc,

log_abc =x-1

bc = a^x-1

= a^x/a

abc = a^x

 (abc)^1/x = a

Similarly

(abc)^1/y =b and (abc)^1/z =c

(abc)^1/x(abc)^1/y (abc)^1/z= abc (By multiplying individual terms)

But

(abc)^1/x(abc)^1/y (abc)^1/z = (abc)^{(1/x+1/y+1/z)}

abc = (abc)^{(1/x+1/y+1/z)}

 1 = [(1/x)+(1/y)+(1/z)] ( By equating exponents)

= (yz/xyz)+(xz/xyz)+(xy/xyz)

= (xy+yz+zx)/xyz

 xyz = xy+yz+zx

Why use Logarithmic and antilogarithmic tables?

 

 

 

 

 

2.3 Summary of learning

 

 

No	Points to remember
1	loga(mn) = loga m+ loga n
2	loga(m/n) = loga m – loga n
3	logamn = nloga m
4	logam1/n  = (1/n) logam
5	logx y= logx a/ logy a
6	logx y = loga y/ loga x