

















2.7 Linear Equations:
Is it not interesting to solve problems similar to?
1.
If sum of three consecutive even numbers is 252, which are
they? (80,82,84 ? 70,72,74 ? . . . )
2.
If the length of a rectangle is 4cms more than breadth and
the perimeter is 11cms more than breadth. What is the length and breadth of the
rectangle?
3.
A traveler on a pilgrimage spends half the amount in Prayaga, 2/9
th of the remaining amount in Kashi, 1/4 th of the remaining
amount towards taxes, 6/10 th of the remaining amount in
Definition : Equation is statement of equality of two algebraic
expressions involving one or more unknown quantities (called Variables).
The expression on Left Hand Side is called (LHS)
and expression on Right Hand Side is called RHS.
Observations:
Is it not true that 6=6 ?
======è (1)
Here Left hand side (LHS) is 6 and Right hand side
is also 6 and both sides are equal
We thus say LHS=RHS (as both sides are equal)
Let us add the same number 2 to both sides of (1)
We get LHS =6+2=8
and also RHS = 6+2 =8
We still notice that LHS= RHS (as both sides are
equal)
Let us subtract the same number 3 from both sides
of (1)
We get LHS= 6-3 =3 and RHS = 6-3 =3
We still notice that LHS=RHS (as both sides are
equal)
Let us multiply both sides of (1) by the same
number 6
We get LHS= 6*6=36 and RHS= 6*6 =36
We still notice that LHS=RHS (both sides are equal)
Let us divide both sides of (1) by
the same number 3
We get LHS = 6/3=2 and RHS = 6/3=2
We still notice that LHS=RHS (both sides are equal)
Properties of Equality (Axioms)
1. Equality does not change when we add same
quantity to both sides
2 Equality
does not change when we subtract same quantity from both sides
3. Equality does not change when we multiply both
sides by same quantity
4. Equality does not change when we divide both
sides by same non-zero quantity
If we carry out any of the above mentioned
operations on an equal statement (LHS=RHS), the equality (LHS+RHS) still holds well
even after the operation.
Definition : An equation
containing only linear polynomial or variable in first degree is called ‘linear
equation’
Eaxmples
: x+2 =5, 3*(a-5) =6, ½ x -4/5 =
3x+7 are all linear equations
x2-4 =0 is not
a linear equation(![]() Its degree is 2)
Its degree is 2)
Example 1:
Let us consider the statement x-3 = 1 where x is a
variable.
This statement can be explained as “find the value
of x, such that, when 3 is subtracted from that number(x) we should get the
result as 1”
Let us substitute the following values for x as in
the statement x-3 =1
1. Can x be 1? No, because 1-3 which is -2, is ![]()
2. Can x be 2 ? No, because 2-3 which is -1, is ![]()
3. Can x be 5? No, because 5-3 which is 2, is ![]()
4. Can x be 4? Yes because 4-3=1.
What are we doing?
We are trying to find the value of x by trial and
error method which is time consuming and is not the most effective way.
If so, then how do we find out the value of x
mathematically?
Let us add 3 to both sides of the statement. Then
we get x-3+3= 1+3 so we get x+0 = 4.
What did we do ?
We added the same number to both sides of the
statement as per 1st Axiom.
Why did we choose the number 3 to be added?
We wanted only x to be present on LHS and no other
number along with x.
Example 2:Find the value of x such that 6x+4 = 3x+10
Here LHS =6x+4 and RHS= 3x+10
Step1:
Subtract 3x from both sides (Why? We want RHS to contain
only the constant and not the variable) then we get
RHS = 3x+10-3x= 10
LHS = 6x+4-3x = 3x+4
From 2nd Axiom, RHS=LHS
Step 2:
Subtract 4 from both sides (Why? We want LHS to
have only the variable part and not the constant) then we get
LHS = 3x+4-4=3x
RHS = 10-4 = 6
From 2nd Axiom, LHS=RHS
Step 3
Divide both sides by 3
(Why? We want LHS to have only variable with co-efficient=1) then we get
LHS = 3x/3 =x
RHS = 6/3 =2
From 2nd Axiom, LHS=RHS
Thus we have x=2
What did we do in first
two steps?
We first subtracted 3x
from both sides and then the constant (number) 4.
This is same as saying
add additive inverse of 3x (i.e. -3x)
and additive inverse of 4 (i.e. -4) to both LHS and RHS
We transposed
(changed) 3x from one side to another
side of the equation with change in sign and then in 2nd step, transposed 4 from one side
to another side of equation with change in sign
Let us summarise our
steps
|
Step |
Statement |
Explanation |
|
1 |
6x+4= 3x+10 |
Given equation: |
|
2 |
6x+4-3x =10 i.e. 3x+4 =10 |
Transposition of 3x from
right side to left side with sign changed |
|
3 |
3x= 10-4 i.e. 3x =16 |
Transposition of 4 from left
side to right side with change in sign |
|
4 |
x=2 |
Simplification(Divide both sides
by 3) |
Verification:
Let us replace x by 2
in the equation (1)
LHS =6*2+4 = 16 and
RHS = 3*2+10 =16
Since LHS =
RHS=16, x=2 is the correct answer.
Definition: Finding the value of variable
which when substituted in the equation makes two sides (LHS and RHS) equal, is
called ‘solution’ to the equation.
In the above case x =2
is the solution to the equation. You may notice that x=1 is not a solution to
the above equation (because when 1 is substituted for x, we get LHS = 10 and
RHS=13 and therefore LHS ![]() )
)
2.7 Problem 1 : Solve (Find value of x) in
5*(2x-3) =
2*(3x-7)
Solution:
|
Step |
Statement |
Explanation |
|
1 |
5*(2x-3) = 2*(3x-7) |
Given equation: |
|
2 |
10x -15 = 6x -14 |
Simplification |
|
3 |
10x -6x= -14+15 |
Transposition of 6x,15 from one
side to another with sign change |
|
4 |
4x = 1:i,e x = ¼ |
Simplification |
Verification:
Substitute 1/4 for x in
the given equation (1)
LHS = 5*(2*1/4 -3) =
5*(1/2-3) = 5*(-5/2) = -25/2
RHS = 2*(3*1/4-7) = 2*(3/4-7) = 2*(-25/4) = -25/2
Since LHS= RHS = -25/2,
x =1/4 is the correct answer
2.7 Problem 2 : Solve for x
![]() = 1/2
= 1/2
Solution:
Get the squares of both
sides
(x-2)/(x+1) = 1/4
On cross multiplication
we get
4(x-2) = x+1
I.e. 4x – 8 = x+1
(simplification)
I.e. 4x –x = 1+8 ( Transposition)
I.e. 3x = 9
![]() x=3
x=3
Verification:
Substitute x=3 in the
given problem to note that ![]() = 1/2
= 1/2
2.7 Problem 3: Find three consecutive even
numbers whose sum is 252
Solution:
Step 1 : Let x be the
first even number
Step 2 : Then the next
two consecutive even numbers are x+2 and x+4
Step 3 : Sum of these
three consecutive even numbers are
x+(x+2)+(x+4) = 3x+6
LHS = 3x+6
RHS = 252(Given data)
We need to solve 3x+6 =
252
On transposition we get
3x = 252-6=246 and thus x = 82
The three numbers are
82(=x), 84(=x+2) and 86(=x+4)
Verification:
82, 84, 86 are three
consecutive even numbers
and their sum is =
82+84+86 which is = 252
2.7 Problem 4: A steamer goes downstream from one
port to another in 9 hours. It covers the same distance upstream in 10hours. If
the speed of stream be 1km per hour, find out the distance between ports
Solution:
|
Step1: Let the speed of steamer
in still water be x km per hour. The speed of downstream = (x+1)
km per hour. The speed in upstream = (x-1) km per hour. The distance covered in 9hours
while going down =9(x+1). The distance covered upstream in 10hours = 10(x-1) Step 2: Since distance between 2
ports is same (going upstream or going downstream) 9(x+1) = 10(x-1) Step3: We need to solve the
equation 9x+9 =10x-10i.e. 9+10 =10x-9x(By transposition) Therefore 19=x .Substitute this
value in 9(x+1) The distance covered while in
downstream =9(x+1) = 9*(19+1) =9*20= 180km |
|
Verification:
Speed of steamer while
going downstream = (distance/time) – (speed of stream) = (180/9)-1 = (20-1) km/hr=19km/hr
Speed of steamer while
going upstream = (distance/time) +
(speed of stream) = (180/10) +1 = (18+1) km/hr=19km/hr
Since both are same,
our solution is correct.
2.7 Problem 5: A number consists of 2 digits. The
digit in tens place is 2 times the digit at the units place. The number formed
by reversing the digits is 27 less than the original number. Find the original
number
Solution:
|
1)Let
x be the digit in unit place. Since
the digit in 10’s place is 2 times the digit in units place, it has to be2x.
Since the number consists of 2 digits, its value = 10*digit in 10’s place +
digit in units place Thus
the number = 10*2x+x. =20x+x
-------------è (1) When
we reverse the digits of this number we get the reverse number x 2x(x in tens
place and 2x in units place) whose value= 10* digit in 10’s place + digit in
units place =
10*x+2x =10x+2x --------------è reversed number It
is given that reversed number = oldnumber-27 ie
27 = 21x-12x (By transposition of 12x and 27) i,e 27 =9x
Hence
the original number is 63(digit in tens place is twice the digit in units
place) |
|
Verification:
Since the original number is 63, the reversed
number is 36. 36 is 27 less than 63.
Thus reversed number is 27 less than original
number (which is as given in the problem).
Hence we have solved the problem correctly
2.7 Problem 6: The length
of a rectangle is 4cms more than breadth and the perimeter is 11cms more than
breadth. Find the length and breadth of the rectangle.
Solution:
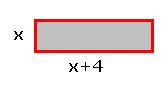
Step 1: let x be the breadth. Then length = x+4.
We know perimeter P = 2*length + 2*breadth =
2(x+4)+2x =2x+8+2x --------------èEquation (1)
We are also given that perimeter is 11cm more than
breadth ( ie P = x+11) --------------è Equation (2)
Step 2 : Both are perimeters of the same rectangle
and hence they have to be equal:
So Equation (1) = Equation (2)
I.e. 2x+8+2x = x+11:
I.e.4x+8 = x+11
I.e. 4x-x = 11-8(By transposition of x and 8):
I.e.3x = 3:
![]() x = 1.
x = 1.
Therefore breadth =1cm and length=5cms(x+4)
Verification:
The perimeter of rectangle = 2*length + 2*breadth =
2*5+2*1 = 10+2 = 12cms = 11cms +1cm = 11cms +breadth.
Hence we have solved the problem correctly.
2.7 Problem 7: In a
fraction, twice the numerator is 2 more than the denominator. If 3 is added to
each numerator and denominator, the new fraction is 2/3. Find the original
fraction
Solution:
Step1: Let x be the
numerator
It is given that twice the numerator is two more
than the denominator ( That is to say
2*numerator = denominator+2)
Hence denominator =2x-2.
Thus the original fraction is x/2x-2
When 3 is added to denominator the new denominator=
(2x-2) +3=2x+1
When 3 is added to numerator the new numerator =
x+3
Thus the new fraction is (new numerator)/ (new
denominator) = (x+3)/ (2x+1)
Since the new fraction is 2/3 we have
Step2 : 2/3 = (x+3)/(2x+1) --------------è(1)
By Multiplying both sides of (1) by (2x+1), we get
2*(2x+1)/3 = x+3
--------------è(2)
By multiplying both sides of (2) by 3, we get
2*(2x+1) =3(x+3)
I.e. 4x+2 =3x+9 and on transposition of 3x and 2 we
get
4x-3x= 9-2
I.e. x= 7
![]() The original denominator = 2x-2 =14-2=12
The original denominator = 2x-2 =14-2=12
Thus the original fraction was 7/12
Verification:
To get the new fraction, add 3 to both numerator
and denominator so we get the new fraction as 10/15 which is 2/3
This shows that we solved the problem correctly
2.7 Problem 8: Divide 32 in
to two parts such that if the larger is divided by the smaller, the quotient is
2 and the reminder is 5
Solution:
|
Let x
be the larger number and hence 32-x will be the smaller number We
know dividend = quotient*divisor + reminder Therfore
we need to solve the equation: x/(32-x)
= 2+ 5(as reminder) Exercise : Solve x = 2(32-x) +5 to get the answer x=23 and
other number as 9 |
|
2.7 Problem 9: Find a positive value of variable x for which
the given equation x2-9/( x2+5)
= -5/9 is satisfied
Solution:
Given equation is x2-9/(
x2+5) = -5/9
On cross multiplication
we get 9(x2-9) = -5(x2+5)
On simplification we
get 9x2-81 = -5x2 -25
On transposition 14x2
= 56
![]() x2 = 4
x2 = 4
![]() x = +2 or -2
x = +2 or -2
Verification:
Substitute x=2 in the
given equation to arrive at LHS = -5/9 which is RHS and hence x=2 is correct
2.7 Problem 10: Of the group of butter flies, 1/5 th proceeded
towards Kadamba tree, 1/3 of the group
proceeded towards Shilindhra tree, thrice the differences of the above two
groups proceeded towards Kutaja tree. If the remaining only one was flying
around attracted by aroma of ketakamalati flowers, Lilavati tell me the count
of butter flies.
( Lilavati Shloka 56)
Solution:
Let the
number of butter flies be x.
|
Step |
To where |
How many |
|
1 |
Kadamba tree |
(x/5) |
|
2 |
Shilindhra tree |
(x/3) |
|
3 |
differences of the above |
(x/3) – (x/5) = (2x/15) |
|
4 |
Kutaja tree |
3*(2x/15)=(2x/15) |
|
5 |
Remaining |
1 |
![]() x- {(x/5)+(x/3)+(2x/5) =1
x- {(x/5)+(x/3)+(2x/5) =1
![]() {15x-(3x+5x+6x)/15} =1
{15x-(3x+5x+6x)/15} =1
![]() x=15
x=15
Verification:
15=3+5+6+1
2.7 Problem 11: A
traveler on pilgrimage spends half the amount in Prayaga, 2/9
th of the remaining amount in Kashi, 1/4 th of the remaining
amount towards taxes, 6/10 th of the remaining amount in
Solution:
Let the number of butter flies be x.
|
Step |
To where Towards |
How much |
Balance |
|
1 |
Prayaga |
(x/2) |
x-(x/2)
= (x/2) |
|
2 |
Kashi |
(2/9)*(x/2)=(x/9) |
(x/2)-(x/9) = (7x/18) |
|
3 |
Taxes |
(1/4)*(7x/18) =(7x/72) |
(7x/18) - (7x/72)=
(21x/72) =(7x/24) |
|
4 |
|
(6/10)*(7x/24)=(7x/40) |
(7x/24)- (7x/40)
={(35x-21x)/120}=(7x/60) |
|
5 |
Remaining |
63 |
|
![]() (7x/60)
=63
(7x/60)
=63
![]() x=540
x=540
Verification:
Try yourself
2.7 Summary of
learning
|
No |
Points studied |
|
1 |
Transposition
of terms from LHS to RHS with change
in sign |
|
2 |
Simplify
LHS and RHS such that variables are on one side and constants are on the
other side. |








