6.11 Circles - Part 2:

                                                                                                                                                                              

6.11.1 Construction of chords

 

1. Construction of chord in a circle.               

 

6.11.1 Problem 1: Construct a chord of length 3cm in a circle of radius 2cm

 

Step

Construction

1

Draw a circle of radius 2cm with O as center.

2

Mark any point P on the circle

 

3

With P as center and 3cm as radius, draw an arc to cut the circle at Q

 

4

Join P and Q ( PQ is the chord of length 3cm)

 

 

 

 

 

 

 

 

 

 

 

 

          Note that this chord divides the circle into 2 regions called segments (PSQ and PTQ).

PSQ is smaller in size as compared to PTQ.

Note that the diameter POR (4cm) is the chord of maximum length.

 

Definition: The region bounded by the chord and an arc is called ‘segment’ of the circle.

 

Observations:

1. Diameter is the chord having maximum length.

2. A chord cuts the circle into 2 segments.

3. Diameter cuts the circle into 2 equal segments (semi circles).

 

2. Finding distance between chord and center of the circle.

 

6.11.1 Problem 2: Construct a chord of length 4cm in a circle of radius 2.5cm and measure the distance between the centre of the circle

and the chord.

 

Step

Construction

1

Draw a circle of radius 4cm with O as center

 

2

Mark any point P on the circle

 

3

With P as center and 4cm as radius, draw an arc to cut the circle at Q

 

4

Join P and Q ( PQ is the chord of length 4cm)

 

5

Bisect the line PQ to find its mid point M. (With P and Q as centers, draw arcs of radius more than half the length of PQ on both sides of PQ and let these arcs meet at R and S). Let RS Meet PQ at M.

6

OM is the distance between chord PQ and center O. We notice that OM=1.5cm

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

            Exercise: Construct few more chords of length 4cm and measure their distance from the center.

 

Observations:

1. As the length of the chord increases, the distance between the chord and the center decreases and becomes 0 for the diameter.

2. As the length of the chord decreases, the distance between the chord and the center increases and becomes R (radius) finally.

3. Chords of equal lengths are equidistant from the center.

 

 

No

 

              Figure

 

 

Properties of angle at circumference

1

ASBA is a minor segment.

 

 

ACB is angle at the circumference and is formed by the minor segment ASBA.

 

 

Minor arc(ASB) subtends acute angle(ACB) at the circumference.

2

ASBOA is a semi circle.

 

ACB is angle at the circumference and is formed by the semi circle ASBOA. Note that ACB = 900.

 

 

Semi circle subtends a right angle at the circumference.

3

 

ASBA is a major segment.

 

 

ACB is angle at the circumference and is formed by the major segment ASBA.

 

 

 

Major arc subtends obtuse angle at the circumference.


   Have you observed race tracks in your annual sports day? All of them are circular tracks with different radii?

 

Definition:

Circles having same center but different radii are called ‘concentric circles’.

A straight line which cuts the circle at 2 distinct points is called ‘secant’.

 

No

Figure

Properties

1

Circles having same center but different radii are called ‘Concentric circles’.

 

 

 

 

C1, C2 and C3 are 3 circles with different radii OA, OB and OC but with the same center O.

 

2

Circles have same radii but different centers are called ‘Congruent circles’.

 

 

 

C1 and C2 are 2 circles having same radii OA (OA=OB) but different centers.

3

A straight line which cuts the circle at 2 distinct points is called ‘Secant’.

 

 

AD is a straight line which cuts the circle at 2 points, B and C.

 

 

ABCD is a Secant.

4

A straight line which meets the circle at only one point is called ‘Tangent’.

 

The point where the line touches the circle is called ‘Point of contact’(P)

 

XY is a straight line which touches the circle at only one point P.

 

XPY is a tangent to the circle at P.


Theorem: The tangent at any point of a circle and the radius through this point are perpendicular to each other

(In the below mentioned figure, Prove that OP is perpendicular to RS).

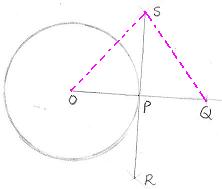
Hint :

Construction: Extend OP such that OP=PQ, Let SR be the bisector of OQ.

Prove that the triangles OPS and QPS are congruent using SSS postulate.

 

1. Construction of tangent at a point on a circle

 

Step

Construction

1

Draw a circle of given radius (2cm) with center as O

2

Mark any point P on the circle

3

Join OP (this becomes radius)

4

Extend OP to Q such that OP=PQ (P is midpoint of OQ)

5

Construct a perpendicular line to OQ at P (With O and Q as centers, draw arcs of radius more than half the length of OQ on both sides of OQ and let these arcs meet at S and R)

6

The line SPR is the tangent at P to the circle

 

 

 

 

 

 

 

 

 

 

 

 

 

Note: Since SP is perpendicular to OQ, OPS = 900

 

2. Construction of tangent to a circle from an external point

 

6.11.1 Problem 3: Construct a tangent to a circle of radius 2cm from a point 5cm away from the center.

 

Step

Construction

1

Draw a circle of given radius (2cm) with center as O

2

Mark any point P at a given distance (5cm) away from the center O, Join OP

3

Bisect the line OP (With O and P as centers, draw arcs of radius more than half the length of OP on both sides of OP and let these arcs meet at R and S)

4

Let RS meet OP at M (Note that M is mid point of OP)

5

Draw arcs of radius = OM with M as center, to cut the circle at X and Y

 

 

 

 

 

 

 

 

 

 

 

 

 

PX and PY are tangents to the circle from P.

 

Observe that from a point within a circle we can not draw any tangent, from a point on a circle we can draw only one tangent and from an

external point we can draw only two tangents to a circle.

 

Let us observe the figure on the right hand side.

C1 is a circle with O as center.C2 is a circle with P as center.

G and H are points on the circles C1 and C2 respectively.

The straight line AB touches the circle C1 at G and C2 at H.

We notice that AB is a tangent common to both the circles C1 and C2 and is called common tangent.

Similarly XY is a common tangent to circles C1 and C2.

In the this figure we notice that centers of both the circles are on the same side of tangent

 

 

Definition: A tangent which is common to two or more circles is called a ‘common tangent’.

Let us observe the figure on right hand side.

 

C1 is a circle with O as center. C2 is a circle with P as center.

 

The two circles touch at Y.

 

XYZ is a tangent common to both the circles at Y.

 

In this figure, we notice that centers of both the circles are on different sides of the tangent.

 

Though the two figures have common tangents, have you observed the position of centers in both the cases?

 

Definition: If the centers of the circles lie on the same side of the common tangent then that tangent is called ‘Direct common tangent’.

If the centers of the circles lie on different sides of the common tangent then that tangent is called ‘Transverse common tangent’.

 

3. Construction of Direct common tangents to 2 circles of equal radii whose centers are at a given distance from each other

 

6.11.1Problem 4:  Draw direct common tangents to 2 circles of radii 2cm whose centers are 5cm apart.

 

Step

Construction

1

Draw a line OP=5cm

2

Draw 2 circles, C1 and C2 of radii 2cm with O and P as centers

3

Extend OP in both directions so that it cuts C1 at X and C2 at Y.

Let OP cut C1 at R and C2 at S

4

Bisect the line XR  (with X and R as centers, draw arcs of radius more than half the length of XR on both sides of XR).

5

Similarly bisect the line SY

6

Let RO cut the circle C1 at A and C. Similarly let SP cut the circle C2 at B and D.


AB and CD are the direct common tangents to the 2 circles.

 

4. Construction of direct common tangent to two circles of different radii.

 

6.11.1 Problem 5: Construct direct common tangents to 2 circles of radii 3cm and 2cm whose centers are 6.5cm apart.

 

Step

Construction

1

Draw the circle C1 of radius 3cm with A as center

2

Let AB = 6.5cm

3

Draw the circle C2 of radius 2cm with B as center

4

Draw the circle C3 of radius of 1cm (difference between radii of C1 and C2 =3-2) with A as center

5

Bisect the line AB to get its mid point M (with A and B as centers, draw arcs of radius more than half the length of AB on either sides of AB to meet at C and D). Join CD to cut AB at M

6

With M as center and AM as radius, draw an arc to cut C3 at X. BX is tangent to C3 at X

7

Produce AX to meet C1 at P

8

Draw a line from B, parallel to AXP (use set squares). Let this line cut C2 at R

9

Join PR. PR is the direct common tangent to the given 2 circles

 

5. Construction of transverse common tangent to two circles.

 

6.11.1 Problem 6: Construct transverse common tangent to circles of radii 2cm and 1 cm whose centers are 5.5 cm apart.

 

Step

Construction

1

Draw the circle C1 of radius 2cm with A as center

2

Let AB = 5.5cm

3

Draw the circle C2 of radius 1cm with B as center

4

Draw the circle C3 of radius 3cm (sum of radii of C1 and C2 =2+1) with A as center

5

Bisect the line AB to get its mid point M (with A and B as centers, draw arcs of radius more than half the length of AB on either sides of AB to meet at C and D). Join CD to cut AB at M

6

With M as center and AM as radius, draw an arc to cut C3 at X. BX is tangent to C3 at X

7

Join XA to meet C1 at P

8

Draw a line from B parallel to APX (use set squares).Let this line cut C2 at R

9

Join PR. PR is the transverse common tangent to the given 2 circles

 

Did you notice the difference between the above two constructions? In the case of direct common tangent, we draw a third circle with radius

equal to the as difference between radii and in the case of transverse common tangent, we draw a third circle with radius equal to the

sum of radii. Except for this difference all other steps are same.

 

6.11 Summary of learning

 

 

No

Points to remember

1

From an external point we can draw two tangents to a circle.

2

The radius drawn at the point of contact is perpendicular to the tangent