Touching Circles

6.14 Touching Circles

Theorem: If two Circles touch each other internally or externally, the point of contact and the centers of the circles are collinear.

Data: Two circles with centers A and B each other externally at point P (Figure 1)) or internally (Figure 2).

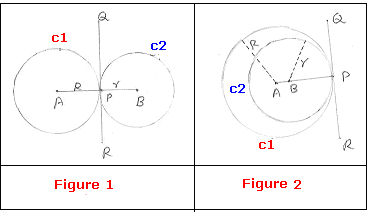
To prove: A, B and P are collinear

Construction: Draw the common tangent RPQ at P. Join AP and BP

Proof: (When circles touch externally)

Step	Statement	Reason
1	APQ = 90⁰=BPQ	RQ is tangent to the circles at P, AP and BP are radii
2	APQ+BPQ = 180⁰	From step 1
3	APB is a straight line	Angles APQ andBPQ is a linear pair
A, B and P are collinear

Proof: (When circles touch internally)

Step	Statement	Reason
1	AP and BP are perpendicular to same line RQ	RQ is tangent to circles at P, AP and BP are radii
2	B is a point on line AP
3	ABP is a straight line	Step 2
A, B and P are collinear

6.14 Problem 1: A straight line drawn through the point of contact of two circles whose centers are A and B, intersect the circles at P and Q

respectively. Show that AP and BQ are parallel.

In the adjoining figure circles with origins A and B, touch externally at M. We need to prove that AP || BQ.

Step	Statement	Reason
1	AM=AP	Radii of same circle
2	APM = AMP	2 sides are equal
3	AMP= QMB	Vertically opposite angles
4	BM=BQ	Radii of same circle
5	QMB = BQM	2 sides are equal
6	APM = BQM	Steps 2, 3 and 5
7	AP \|\| BQ	APM, BQM are alternate angles

6.14 Problem 2: In the given figure AB is line segment, M is the midpoint of AB. 2 semi circles with AM and MB as diameters are drawn on the

line AB. A circle with center as O touches all the three circles.

Prove that the radius of this circle is (1/6)AB

Let the radius of this circle be x : OR=OP =x, and AB=a

CP = CM= a/4 and MR=a/2

Step	Statement	Reason
1	OMC is right angled triangle	OM is tangent at M to circle C₁
2	OC² = MC²+OM²	Pythagoras theorem on OMC
3	LHS = (x+(a/2))² = x²+ax/2+ (a²/16)	OC = OP+PC = x+(a/4)
4	RHS = (a²/16)+ (a²/4)-ax+ x²	MC=a/4,OM = MR-OR=a/2-x
5	x²+ax/2+ (a²/16) =(a²/16)+ (a²/4)-ax+ x²	Equating LHS and RHS
6	3ax/2=(a²/4)	On transformation
7	x = a/6

6.14 Theorem: The tangents drawn to a circle from an external point are

(i) Equal

(ii) Equally inclined to the line joining the external point and the center

(iii) Subtend equal angles at the center

Data: PA and PB are tangents from P to the circle with origin at O

To Prove

(i) PA=PB

(ii) APO= BPO

(iii) AOP= BOP

Proof:

Step	Statement	Reason
1	OA = OB	Radii of same circle
2	OAP= OBP= 90⁰	PA and PB are tangents at A and B and AO and BO are radii
3	OP is common side of AOP, BOP
4	AOP BOP	SAS Postulate of Right angled triangle
5	PA=PB	Properties of congruent triangles
6	APO= BPO	Properties of congruent triangles
7	AOP= BOP	Properties of congruent triangles

6.14 Problem 3: In the figure, XY and PC are common tangents to 2 touching circles. Prove that XPY = 90

Step	Statement	Reason
1	CX= CP	CX and CP are tangents from C
2	CXP =CPX =x⁰	2 sides are equal
3	CY =CP	CY and CP are tangents from C
4	PYC =CPY =y⁰	2 sides are equal
5	CXP + XPC + CPY +PYC = 180⁰	Sum of all angles in a triangle
6	i.e. x⁰+x⁰+y⁰+y⁰= 180⁰
7	2(x⁰+y⁰)= 180⁰
8	i.e. (x⁰+y⁰) =XPY = 90⁰

6.14 Problem 4: Tangents PQ and PR are drawn to the circle from an external point P. If PQR = 60⁰ prove that the length of the

chord QR = length of the tangent

Step	Statement	Reason
1	PQ=PR	PQ and PR are tangents from P
2	PQR =PRQ	2 sides are equal
3	PQR =60⁰	Given
4	PQR =PRQ = 60⁰	Step 2
5	PQR is an equilateral triangle	All angles are = 60⁰
6	PQ=PR=QR

6.14 Problem 5: In the figure PQ and PR are tangents to the circle with Center O. If QPR= 90⁰. Show that PQOR is a square.

Step	Statement	Reason
1	OQP= 90⁰ =ORP	PQ and PR are tangents from P
2	QPR=90⁰	Given
3	OQ is parallel to PR	Corresponding angles are 90⁰
4	QOR =360⁰-OQP-QPR -ORP = 360⁰-90⁰-90⁰-90⁰	Property of quadrilateral
5	OR is parallel to QP	Corresponding angles are 90⁰
6	PQOR is a parallelogram
7	PQOR is a square	OQ=OR(radii)

6.14 Problem 6: In the figure, AT and BT are tangents to a circle with center O. Another tangent PQ is drawn such that TP=TQ.

Show that TAB ||| TPQ

Step	Statement	Reason
1	AT=BT	TA and TB are tangents from an external point T
2	TAB=TBA	2 sides are equal
3	PT=QT	TP and TQ are tangents from an external point T
4	TPQ=TQP	2 sides are equal
5	ATB= 180⁰- (TAB+TBA)= 180⁰- 2TAB	InTAB, sum of all the angles = 180⁰
6	ATB= 180⁰- (TPQ+TQP)= 180⁰- 2TPQ	InTPQ, sum of all the angles = 180⁰
7	TAB =TPQ	Equate RHS of steps 5, 6
8	TAB =TPQ=TQP =TBA	Steps 7, 4, 2
9	TAB \|\|\| TPQ	Triangles are equiangular

6.14 Problem 7: In the given figure, tangents are drawn to the circle from external points A, B and C. Prove that

1) AP+BQ+CR = BP+CQ+AR and AP+BQ+CR = 1/2 *perimeter of ABC.

2) If AB=AC, prove that BQ=QC

Step	Statement	Reason
1	PA=AR	Tangents to circle from A
2	BQ=BP	Tangents to circle from B
3	CR=CQ	Tangents to circle from C
4	PA+BQ+CR=AR+BP+CQ	Addition of steps 1 to 3
5	AB=AP+PB, BC=BQ+QC, AC=AR+RC
6	AB+BC+AC = PA+BQ+CR +AR+BP+CQ	Addition of step 5
7	= 2 (AP+BQ+CR) = Perimeter of ABC	From Step 4
Second part
8	AB=AC	Given
9	AP+PB=AR+RC
10	PB=RC	Since AP = AR, Step 1
11	BQ=CQ	Steps 2 and 3

6.14 Problem 8: TP and TQ are tangents drawn to a circle with O as center.

Show that

1. OT is perpendicular bisector of PQ

2. PTQ =2OPQ

Step	Statement	Reason
Consider TPR and TQR
1	TP=TQ, PTR=QTR	6.14 Theorem(TP and TQ are tangents)
2	TR is common
3	TPR TQR	SAS Postulate on congruence
4	PR=RQ and PRT=QRT	Corresponding sides are equal
5	PRT = 90⁰	Two equal angles on a straight line
Second Part
6	PTR +RPT = 90⁰	Sum of two angles in a right angled triangle PRT
7	OPT =90⁰=OPR+RPT	PT is tangent and OP is radius P = 90⁰
8	PTR =OPR	Steps 6 and 7
9	PTQ = 2 PTR	Step 1
10	= 2 OPR	Step 8

Note: Above problem can also be solved by using the properties: OP=OQ and OPT = 90⁰

6.14 Summary of learning

Points to remember

The tangents drawn to a circle from an external point are

-equal,

-equally inclined to the line joining the external point and circle,

-subtend equal angles at the center.

Additional Points:

6.14. Theorem 1: A tangent at any point on the circle is perpendicular to the radius through that point.

6.14. Theorem 2: The line perpendicular to a radius at its outer end is a tangent to the circle.

Above two theorems can be proved by logical reasoning (First we make an assumption that the theorem is not true. Subsequently,

because of a contradiction, we conclude that our assumption is wrong. Then by logical reasoning we conclude that theorem is true.)

6.14.Theorem 3: If a chord(AB) and a tangent(PT) intersect externally, then the product of lengths of the segments of the chord (PA.PB)

is equal to the square of the length of the tangent(PT²)from the point of contact(T) to the point of intersection (P).

Given: PT is tangent, AB is chord.

To prove: PA.PB = PT²

Construction: Join O to the mid point M of AB, Join OA.

Step	Statement	Reason
1	PA = PM-AM	Construction
2	PB = PM+MB	Construction
3	= PM+AM	MB=AM(Construction)
4	PA.PB = (PM-AM)*(PM+AM)	Product of Steps 1 and 3
5	= PM²-AM²	Expansion
6	PM²= PO²-OM²	Pythagoras theorem on POM
7	AM²= AO²-OM²	Pythagoras theorem on AOM
8	PA.PB = PO²- AO²	Substitute results from Step 6 and 7 in Step 5
9	= PO²-TO²	AO=TO(Radii)
10	PA.PB = PT²	Pythagoras theorem on PTO

6.14. Theorem 4 (Tangent-Secant theorem or Alternate Segment theorem): The angle between a tangent (PQ) and a chord (AB)

through the point of contact is equal to an angle in the alternate segment.

Given: PQ is a tangent at A to the circle with O as center. AB is a chord.

To prove: If C is a point on a major arc and D is a point on a minor arc with respect to the chord AB then

BAQ = ACB and PAB = ADB

Construction: Join OB

Step	Statement	Reason
1	OAQ = 90⁰	The line drawn from point of contact to center is at right angle to the tangent
2	OAB = 90⁰- BAQ	Split OAQ
3	BAO = ABO	OA=OB(Radii) hence OAB is an isosceles triangle
4	AOB = 180⁰- 2OAB	Sum of all angles in AOB is 180⁰and step 3
5	= 180⁰– 2 (90⁰- BAQ)	Step 2
6	= 2BAQ	Simplification
7	AOB = 2ACB	Angles on the same chord AB at center and circle (Refer 6.8.2 Inscribed angle theorem)
8	BAQ = ACB	Steps 6 and 7
9	PAB + BAQ = 180⁰	Angles on the straight line
10	ADB + ACB = 180⁰	Opposite angles in a cyclic quadrilateral are supplementary (Refer 6.9.3)
11	PAB = ADB	Steps 8,9 and 10