6.2 Axioms, Postulates and Enunciations on lines:

 

6.2.1 Axioms

In geometry we have to accept some facts, without discussion and proof. They are called axioms and postulates. Axiom means ‘Saying’

as per English dictionary. Axioms are required more in Geometry than in other branches of mathematics. They  are  self evident truths

formed as a result of observations and intuition.

Definition:

 

‘Axiom’ is a statement, the truth of which is accepted without any proof.

Notes :

1.   Axioms should not contradict each other. They must be consistent

2.   Axioms should be independent(No axiom should be created based on another axiom)

3.   Axioms should be minimum in numbers.

 

   1. In Algebra, we know that if a=b and b=c then a=c  

 

 

 

 

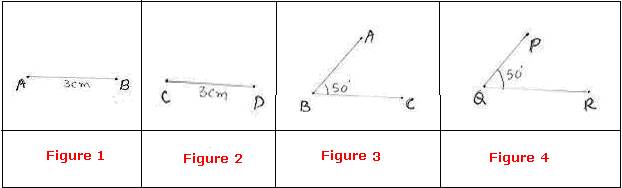
In Figure 1, length of AB=3cm and in Figure 2, length of CD=3cm, then we say that AB=CD..

In Figure 3, ABC = 500 and in Figure 4, PQR = 500, then we say that ABC = PQR.

 

In Geometry this property is stated as an axiom as follows:

 

6.2.1 Axiom 1:  Things which are equal to the same thing are equal to one another.

 

 

     2. In Algebra, we know that if a=b then a+c=b+c   for any c

  

 

  

 

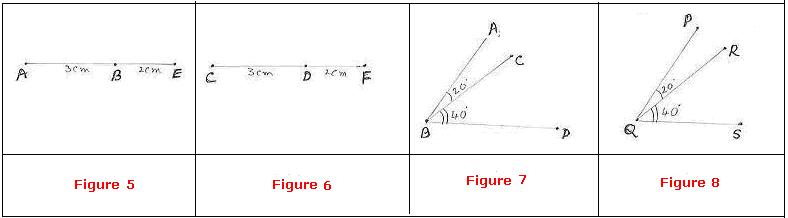
In Figure 5, AB=3cm and BE=2cm. In Figure 6, CD=3cm and DF =2cm.

If BE and DF are added to AB and CD respectively then we have AE=AB+BE=5cms and CF=CD+DF=5cm and we say AE=CF

In Figure 7, ABC = 200 and CBD = 400. In Figure 8, PQR = 200 and RQS = 400.

If CBD and RQS are added to ABC and PQR respectively then we haveABD= 600 and PQS = 600 and we say ABD =PQS.

In Geometry this property is stated as an axiom as follows:

 

6.2.1 Axiom 2:  If equals are added to equals then the result is also equal

 

 
3. In Algebra, we know that if a=b  then a-c=b-c

 

 

 

 

In Figure 9, AE=5cm and BE=2cm. In Figure 10, CF=5cm and DF =2cm.

If BE and DF are subtracted from AE and CF respectively then we have AB=AE-BE=3cms and CD=CF-DF=3cm and we say AB=CD.

In Figure 11, ABD = 600 and CBD = 400. In Figure 12, PQS = 600 and RQS = 400.

If CBD and RQS are subtracted from ABD and PQS respectively then we haveABC = 200 andPQR = 200 and we say ABC =PQR.

In Geometry this property is stated as an axiom as follows:

 

6.2.1 Axiom 3:  If equals are subtracted from equals then the result is also equal

 

 

4. In Algebra, we know that if n >1   then a > a/n 

 

 

  

 

In Figure 13, compare AB with AE and EB, We say that AB>AE and AB>BE.

In Figure 14, compare ABC with ABD and DBC. We say that ABC >ABD and ABC >DBC.

In Geometry this property is stated as an axiom as follows:

 

6.2.1 Axiom 4:  The whole is greater than its parts

 

                                                                  

 

Note: These axioms are used in any branch of Mathematics and not necessarily only in Geometry.

 

6.2.2 Postulates:

 

English dictionary gives the meaning for postulate as ‘guess’ or ‘propose’ or ‘assume’.

 

Definition: ‘Postulates’ are mathematical statements in geometry, which are assumed to be true without proof.

They are like axioms but they can be cross verified by actual construction and measurements.

 

Have you ever thought about how people mark the lanes for 100 meters running race?

 

They identify two points which are 100 meters apart and draw the line joining these two points with chalk powder. Are they using any rule of geometry?

 

 

In the adjacent figure, A and B are two points and AB is the line passing through them.

 

                                      

This property is stated as a postulate as follows:

 

6.2.2 Postulate 1:  One and only one line can be drawn passing through two points.

 

Is it not interesting to note that without knowing this postulate, lanes/tracks are marked by workmen?

Have you thought of any assumption that is made when spokes of the bicycle are joined at the center of the wheel?

 

In the adjacent figure O is the center of the wheel and several lines (spokes) pass through it.

 

    

                 

This property is stated as a postulate as follows:

 

6.2.2 Postulate 2:  Any number of lines can be drawn passing through a point.

 

Spokes in the wheel of a bullock cart/bicycle is a best example of use of this postulate.

In the adjacent figure PQ is a line which is extended on both sides.

 

                 

This property is stated as a postulate as follows:

 

6.2.2 Postulate 3:  A straight line can be extended to any length on both sides

 

In the adjacent figure, two rays are drawn in opposite directions from O (OA and OB). We measure the angle at O and find thatAOB = 1800

 

                      

This property is stated as a postulate as follows:

 

6.2.2 Postulate 4: Angle formed at the common point of two opposite rays is 1800.

 

In how many ways can you sit on the chair? Either you sit with legs crossed or with legs parallel to each other…

 

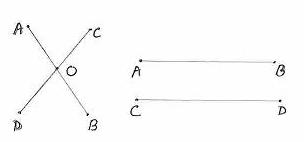
In the adjacent figure the lines AB and CD cross at O or they are parallel to each other.

 

           

This property is stated as a postulate as follows:

 

6.2.2 Postulate 5: Two straight lines either meet at only one point or they do not have a common point.

 

Have you ever thought of what happens if railway lines meet? Journey by Railways will not be possible at all…

In the adjacent figure, lines AB and CD which are parallel, will never meet even if they are extended on both sides (like railway lines).

 

          

This property is stated as a postulate as follows:

 

6.2.2 Postulate 6: Two parallel lines in a plane never meet even if produced infinitely on either side.

 

            Conclusion: From postulates 5 and 6, we conclude that any two straight lines which do not have a common point are parallel to each other.

 

6.2.3 Enunciations/Rules

 

Let us learn what Enunciations are. The English dictionary gives the meaning of Enunciations as ‘guess’ or ‘propose’.

Enunciations are true facts which can only be verified by construction or measurements.

 

In the adjacent figure AOC + COB = 1800

This property is stated as an Enunciation as follows:

 

6.2.3 Enunciation 1: If a ray stands on a straight line, the sum of angles formed at the common point is 1800.

 

This is some time refereed as ‘Linear pair axiom’

In the adjacent figure, the lines AB and CD intersect at O. we notice

AOC = DOB and AOD = COB

 

This property is stated as an Enunciation as follows:

 

6.2.3 Enunciation 2: If two straight lines intersect, the vertically opposite angles are equal.

 

The good example is angles formed in a scissor

 

 

           The above enunciation can also be proved as follows:

 

No

Statement

Reason

1

AOC + COB = 1800

Enunciation 1: AB is a straight line

and OC is standing on AB.

2

DOA + AOC = 1800

Enunciation 1: DC is a straight line

and OA is standing on DC.

3

AOC + COB =DOA + AOC

Axiom 1

4

COB = DOA

Axiom 3(equal thing subtracted is AOC)

 

 

 

 

 

 

 

 

 

Similarly we can prove AOC = DOB.

Definitions:

1. Two angles are said to be ‘adjacent’ if they have a common side and a common end point. (In Figure 1, ABC and CBD are adjacent angles because they have C as common point and BC as common side)

 

2. Two angles are said to be ‘complimentary’, if the sum of their measures is 900(In Figure 2, PQS and SQR are complimentary angles because PQR is a right angle and PQR=900)

 

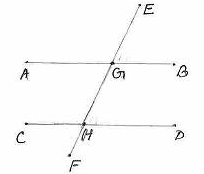
3. Two angles are said to be ‘supplementary’, if the sum of their measures is 1800(In Figure 3, XOZ and ZOY are supplementary angles because OZ is a ray standing on the straight line XOY and XOY = 1800)

 

4. A line which intersects two or more coplanar (on the same plane) lines at different points is called ‘transversal’  (In Figure 4, AB and CD are coplanar lines. EF is the line which cuts AB and CD at G and H respectively. EF is called transversal.)

 

The length of the transversal between parallel lines is called ‘intercept’ In Figure 4, GH is an intercept.

 

 

 

 

 

Examples of different types of angles are:

 

Adjacent Angles

Vertically Opposite Angles(4 pairs)

Alternate Angles

(2 pairs)

Corresponding Angles(4 pairs)

Interior Angles

(2 pairs)

AGE and EGB

AGE and HGB

AGH and GHD

EGB and GHD

AGH and GHC

CHF and FHD

CHF and GHD

BGH and CHG

AGE and CHG

BGH and GHD

…….

AGH and EGB

 

AGH and CHF

 

 

CHG and FHD

 

BGH and DHF

 

 

 

In the adjacent figure, AB and CD are parallel lines and EF is a transversal. Then EGB = GHD, AGH = CHF, AGE =GHC and BGH = DHF.

 

This property is stated as an Enunciation as follows:

 

6.2.3 Enunciation 3: If a transversal cuts two parallel lines, then the corresponding angles are equal.

 

 

6.2.3 Enunciation 4: If a transversal cuts two lines in such a way that the corresponding angles are equal then the two lines are parallel.

(This is converse of Enunciation 3.)

 

6.2 Problem  1 :   In the figure, O is a point on the straight line AB, Line OP stands on AB at O. OQ bisects POB and OR bisects AOP 

Prove that ROQ = 900.

 

Soluition :

No

Statement

Reason

1

POQ = QOB

OQ bisects POB.

2

POB  = 2* POQ

Step 1

3

AOP =2*ROP

OR bisects AOP

4

AOP + POB = 1800

Enunciation 1: AB is a straight line

and OP is standing on AB

5

2* ROP +2*POQ =1800

Step 4,2,3

6

2(ROP +POQ) =1800

Simplification

7

ROP +POQ =900

 

8

ROQ=900

ROP +POQ=ROQ


6.2 Problem 2:   In the figure, O is a point on the straight line AB. Lines OP and OQ stand on AB at O. Find all the angles and show

that QOP is a right angle.

 

Soluition :

No

Statement

Reason

1

AOP+POB=1800

Enunciation 1: OP is standing on AB

2

x+2x = 1800 i.e.3x =1800  i.e.  x =600

Substitution, Simplification

3

AOQ+QOB=1800

Enunciation 1: OQ is standing on AB

4

y+5y = 1800  i.e.  6y = 1800  i.e.  y =300

Substitution, Simplification

5

AOP = x = 600 POB = 2x = 1200  

Substitution

6

AOQ = y =  300 ,QOB = 5y =1500

Substitution

7

QOP = QOA +AOP= y+x =300 + 600 = 900  

Substitution


6.2 Problem 3:   In the figure, O is a point on the straight line AB. If a-b =800, find all angles.

 

Solution:

No

Statement

Reason

1

AOP+POB=1800

Enunciation 1: OP is standing on AB

2

a+b= 1800

Substitution

3

b = 1800-a

By transposition

4

a-b = 800

Given

5

a-b= a – (1800 -a) = 2a -1800

Substitute  value of b in step 4

6

2a -1800=800

Equating 4 and 5

7

2a =800+1800= 2600: 2a =2600

By transposition, Simplification

8

a= 1300:b =500

Simplification, Substitution


 

6.2 Problem 4:   In the figure, OB bisects POQ. OA and OB are in the opposite direction. Prove that AOP = AOQ

 

Solution:

No

Statement

Reason

1

AOP+POB=1800

Enunciation 1: OP is standing on AB

2

AOP = 1800-POB

By transposition

3

POB = BOQ

Given that OB bisects POQ

4

AOP = 1800-BOQ

Substitute 3 in 2.

5

AOQ+QOB=1800

Enunciation 1: OQ is standing on AB

6

AOQ = 1800-BOQ

By transposition

7

AOP = 1800-BOQ=  AOQ

Equating Step 4 and 6

  

6.2 Problem 5:   In the figure, PQ and RS are straight lines. OA bisects POR and OB bisects SOQ. Prove that AB is a straight line.

 

Solution:

No

Statement

Reason

 

 

1

POR = 2AOP

Given that OA bisects POR

2

SOQ = 2BOQ

Given that OB bisects SOQ

3

POR = SOQ

Enunciation 2, vertically opposite angles are equal: PQ and RS are straight lines

4

2AOP = 2BOQ: AOP =BOQ

Substituting 1 and 2 in 3

5

AOB = AOP+POS+SOB

 

6

= BOQ+POS+SOB

Substituting BOQ for AOP  from of step 4

7

=POS+SOB+BOQ

Re arranging  angles

8

= 1800

PQ is a straight line and OS is ray on that line and SOQ =SOB+BOQ. AB is a straight line

  

6.2  Problem 6:   In the figure , ABC = ACB Prove that ACQ =ABP and CBR =BCS

 

 

Solution:

No

Statement

Reason

 

 

 

1

ACB+ACQ = 1800

BC is a straight line.

2

ACB = 1800 – ACQ

By transposition

3

PBA+ABC = 1800

BC is a straight line.

4

PBA = 1800 – ABC

By transposition

5

= 1800 – ACB

it is given that ABC=ACB

6

= 1800 – (1800 –ACQ)

Substitute for ACB from step 2

7

= ACQ

Simplification ( this proves first part)

8

PBR=ABC

They are opposite angles

9

QCS=ACB

They are opposite angles

10

PBR = QCS

From step 8 and 9 and it is given that ABC=ACB

11

CBR = 1800 – PBR

CBR +PBR = 1800

12

= 1800 – QCS

PBR =QCS from step 10

13

=1800 – (1800 – BCS)

QCS+BCS = 1800

14

= BCS

Simplification (this proves second part)

  

6.2  Problem 7:   In the figure, AGE=1200 and CHF = 600. Find out whether AB||CD or not.

EGB and GHD

 

Solution:

No

Statement

Reason

1

CHF = GHD = 600

CHF and GHD are vertically opposite angles and it is given that CHF = 600.

 

2

EGB = 600.

Angles on the straight line AGE + EGB =1800  and it is given that AGE = 1200

 

3

EGB = GHD

Step 1 and 2

 

Since EGB and GHD are corresponding angles and are equal, by Enunciation 4, AB and CD are parallel.

 

6.2 Problem 8:   In the figure, AB||CD, EF cuts them at G and H respectively. If AGE and EGB are in the ratio of 3:2,

find all the angles in the figure.

 

Solution:

Since AB is a straight line, AGE + EGB =1800.

Since the ratio of angles is 3:2, 1800 needs to be split in to two angles as per this ratio. Total parts = 3+2 =5.

5 parts = 1800

1 part = 1800/5 = 360

AGE = 3parts = 3*360 = 1080

EGB = 2parts = 2*360 = 720

No

Statement

Reason

1

AGE = HGB =1080

Vertically opposite angles

2

EGB = AGH = 720

Vertically opposite angles

3

EGB = GHD = 720

Corresponding angles

4

AGE = CHG =1080

Corresponding angles

5

DHF = CHG =1080

Vertically opposite angles

6

CHF = GHD = 720

Vertically opposite angles

                

 

 

 

 

 

 

 

 

 

 

 

 

6.2 Problem 9:   In the figure given below, PQ||RS. Show that QPO + ORS = POR

 

Construction: Draw a line TU parallel to PQ through O, extend SR to Y, extend QP to X, extend RO to V and extend OP to Z.

Soluition :

No

Statement

Reason

 

1

TOP= XPZ

Corresponding angles(XQ||TU)

2

XPZ=QPO

Vertically opposite angle

3

QPO= TOP

Step 1 and 2

4

ROT = VOU

Vertically opposite angle

5

VOU = 1800 -TOV

TOU is straight line

6

TOV = YRV

Corresponding angles(TU||YS)

7

VOU = 1800 -YRV

Step 5 and 6

8

1800 -YRV = ORS

YS is straight line

9

VOU =ORS

Step 7,8

10

ROT = ORS

Step 4,Step 9

11

POR = POT +TOR = QPO+ORS

Step 3 ,Step 10

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6.2 Summary of learning

 

 

No

Points learnt

1

Axioms, Postulates and Enunciations on lines

 

 

Additional points:

 

1.  Two lines which are parallel to the same line are parallel to each other.

2.  Two lines which are perpendicular to the same line are parallel to each other.

3.  Two parallel lines make equal intercepts on all transversals perpendicular to them.

4.  ‘Equal intercepts property’: If three or more parallel lines make equal intercepts on one transversal, then they make equal intercepts on  

     any other transversal as well.

5.  ‘Proportional intercepts property’: Three or more parallel lines intersecting any two transversals make intercepts on them in the same proportion.

 

Dividing line segment in a given ratio:

 

We use the ‘Proportional intercepts property’ for this construction.

 

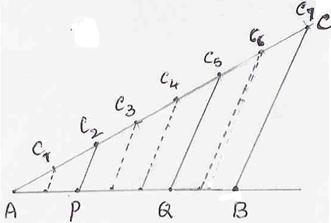
6.2 Problem 11: Divide a line of 5cm in the ratio of 2:3:2

 

No

Construction

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

Draw a line AB = 5cm

2

Draw a line AC such that AC is different from AB

3

Cut the line AC into 7(=2+3+2) equal line segments of any length starting from A (by arcs of equal length)

4

Join the last marked point(C7) on AC with B to get the line C7B

5

Draw parallel lines to C7B, from C2 and C5 to the line AB to cut the line AB at P and Q respectively

6

Join C2P and C5Q

7

AP:PQ:QB = 2:3:2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Note: If we draw lines parallel to C7B from C1,C2,C3,C4,C5,C6 to AB (dotted lines in the figure), these lines cut AB into 7 equal parts

(‘Equal intercepts property’)