Triangles

6.4 Triangles:

6.4.1 Classification and Theorems on triangles

The word Triangle can be split as tri and angle, meaning three angles.

Definition: ‘Triangle’ is a closed figure formed by three distinct (non-collinear) line segments.

Note that triangle has

Three Sides : AB, BC, CA

Three Vertices : A, B, C

Three Angles : ABC, BCA, CAB

Depending upon the measure of angles and sides, triangles are classified as:

Classification	Type	Property	Example
Based on angles	Acute angled triangle	Each angle is less than 90⁰
	Right angled triangle	One angle is 90⁰ PQR =90⁰
	Obtuse angled triangle	One angle is more than 90⁰ BCA > 90⁰
	Equiangular triangle	All angles are equal PQR =QRP =RPQ = 60⁰
	Isosceles triangle	Two angles are equal ABC =BCA
Based on Sides	Scalene triangle	All sides are of different length AB≠BC≠CA
	Equilateral triangle	All sides are equal AB=BC=CA
	Isosceles triangle	Two sides are equal PQ=PR
	Isosceles right angled triangle	A right angled triangle with 2 sides equal ABC =90⁰ And AB=BC

We know that sum of angles in a triangle is 180⁰. Let us prove this, mathematically.

6.4.1 Theorem 1: In any triangle sum of the three angles is 180⁰.

Data: ABC is a triangle

To prove: ABC+BAC +ACB = 180⁰

Construction: Draw a line DE parallel to BC and passing through A

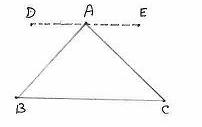
No	Statement	Reason
1	EAB = ABC	By theorem on parallel lines as EF is \|\| BC and AB is transversal.
2	EAC = ACB	By theorem on parallel lines as EF is \|\| BC and A is transversal.
3	EAB+BAC +EAC= 180⁰	Postulate 4: sum of angles on the straight line = 180⁰
4	ABC+BAC +ACB= 180⁰	Substitute ABC for EAB, ACB for EAC in step3

6.4.1 Problem 1: If one angle of an isosceles triangle is 40⁰ find the other two angles.

Solution:

Note: In an isosceles triangle two angles are equal. We also know that sum of all angles in a triangle is 180⁰.

We have two scenarios:

1. Let x be the common angle and 40⁰be the other angle, then we have

x + x + 40⁰= 180⁰

2x =180⁰- 40⁰ = 140⁰

x = 70⁰

The angles of the triangle are 70⁰,70⁰ and 40⁰

2. Let the common angle be 40⁰and other angle be x

Then 40⁰+ 40⁰+ x = 180⁰

80⁰+ x = 180⁰

x = 100⁰

The angles of the triangle are 40⁰,40⁰ and 100⁰.

6.4.1 Problem 2: Find the angles of an equiangular (equilateral) triangle.

Solution:

Note: All The angles of an equiangular (equilateral) triangle are equal. Also sum of all angles in a triangle = 180⁰.

If x is one of the angles of the triangle, then we have x + x + x = 180⁰ i.e. 3x =180⁰. Therefore x = 60⁰

Definition: If any side of a triangle is extended, the angle formed at the vertex is called an ‘exterior’ angle.

In the figure ACD is Exterior Angle

The two angles inside the triangle, opposite to the adjacent angleof the exterior angle are called ‘interior opposite’ angles.

In the figure BAC and ABC are Interior opposite Angles

Figure	Exterior Angle	Interior opposite Angles
k	ACD Observe here that exterior angle is an obtuse angle i.e. ACD > 90⁰)	BAC and ABC
	CBD Observe here that exterior angle is an acute angle i.e. CBD < 90⁰)	BAC and ACB
	ABD Observe here that exterior angle is a right angle i.e. ABD =90⁰)	BAC and BCA

Note that since triangles have three sides, they have three exterior angles.

6.4.1 Theorem 2: If one of the sides of a triangle is extended, the exterior angle so formed is equal to sum of interior opposite angles.

Data: ABC is a triangle

To Prove: ACD = ABC + BAC

Proof:

No	Statement	Reason
1	ABC+BCA +CAB = 180⁰	Theorem : Sum of the angles in a triangle = 180⁰
2	BCA+ACD = 180⁰	Postulate 4: sum of angles on the straight line = 180⁰
3	ABC+BCA +CAB = BCA+ACD	Axiom 1
4	ABC + BAC= ACD	Axiom 2 ( The equals added here is BCA)

Observations:

No	Corollaries of above two theorems(6.4.1)	Reasoning( if x,y,z are three angles of a triangle)
1	Exterior angle > each of the interior opposite angles	If x,y > 0 then x+y >x and x+y > y
2	A triangle can not have more than one right angle	If x+y+z =180, both x and y can not be 90
3	A triangle can not have more than one obtuse angle	If x>90 then y+z <90
4	In every triangle at least two angles are acute	With x < 90, Both y, z can not be >90
5	In a right angled triangle the sum of two other angles = 90⁰	If x=90 then y+z has to be 90 and hence both y,z<90
6	If two angles in one triangle are equal to two angles in another triangle then third angle of both the triangles are equal	x+y+z = 180 and hence z =180-x-y

6.4.1 Problem 3: An exterior angle of a triangle is 90⁰ and one interior opposite angle is 45⁰. Find the remaining angle of the triangle.

Solution:

Let x be the other interior angle of the triangle.

We know that, exterior angle of a triangle = sum of interior opposite angles.

90⁰ = x+45⁰

Hence x = 45⁰.

6.4.1 Problem 4: Find all the angles in the triangle given below.

Solution:

Since 100⁰ is the exterior angle at vertex B, its interior opposite angles are p and q.

p+q = 100⁰ ------(1)

Since 130⁰ is the exterior angle at vertex C, its interior opposite angles are r and q.

r+q = 130⁰------(2)

We also know that p + q + r = 180⁰

100⁰ + r = 180⁰ (By substituting value of p+q in the above equation)

r = 180⁰-100⁰=80⁰

By substituting this value of r in (2) we get q= 50⁰.

By substituting this value of q in (1) we get p= 50⁰.

Therefore 50⁰,50⁰ and 80⁰are the values of p, q and r respectively.

6.4.1 Problem 5: Prove that sum of the angles of a quadrilateral is 4 right angles.

Solution:

Any quadrilateral can be divided in to 2 triangles and sum of angles in a triangle is 2 right angles.

Sum of angles in a quadrilateral = 2*(sum of angles in each of the triangle) = 2*180⁰ =360⁰

6.4.1 Problem 6: If in a triangle ABC, 2(A-20) = B+10= 2(C-10), find each of the angle

Solution:

Note A+B+C =180 and hence B = 180-C-A

Since it is given that 2(A-20) = B+10 I.e. 2A-40 =B+10

I.e. 2A = B+50 = (180-C-A)+50 = 230 –C –A.

By transposition we get 3A = 230-C ------(1)

Since it is given that 2(A-20) = 2(C-10)

I.e. A-20 = C-10 I.e. A = C+10 ----(2)

Substituting this value of A in (1) we get

3A = 3C+ 30 = 230-C I.e. 4C = 200 (On transposition of –C and 30) C = 50

On substituting this value of C in (2) we get A =60.

Substituting value of A and C in A+B+C = 180 we get B = 70

The angles are A = 60, B=70 and C=50.

6.4.1 Problem 7: Prove that bisectors of any two adjacent angles of a rhombus form a right angled triangle

We have to prove that POQ = 90⁰.

Proof:

No	Statement	Reason
1	SPQ+PQR =180⁰	PQRS is a rhombus, and hence PS\|\|QR and interior angles are supplementary
2	2(OPQ+PQO) = 180⁰	It is given that PO and QO bisect SPQ and PQR
3	OPQ+PQO = 90⁰	Step 2
4	POQ = 180- (OPQ+PQO) = 90⁰	Sum of angles in a triangle = 180⁰

6.4.2 Construction of Triangles:

We have seen that a triangle has 3 measurable angles and 3 measurable sides and thus in all has six elements.

But to construct a triangle uniquely, we do not need all the six elements. We just need three elements, one of which has to be a side.

6.4.2.1. Construction of a triangle when 3 sides are given

6.4.2 Problem 1: Construct a triangle ABC with AB = 3cm, BC = 4cm and AC = 5cm.

Method:

First draw a rough figure of the triangle ABC.

No	Steps
1	Draw a line and mark a point A on that line
2	With A as center, cut an arc of radius 3cm to the cut the above line at B (AB=3cm)
3	With A as center cut a large arc of radius 5cm.
4	With B as center cut a large arc of radius 4cm.
5	Let the arcs drawn in steps 3 and 4 meet at C
6	Join AC and BC: ABC is the required triangle

6.4.2 Problem 2: A field is in the shape of an equilateral triangle. Perimeter of the field is 2490 Meters. Construct the triangle with suitable scale.

Solution:

We know that the perimeter of a triangle is the sum of all its side. Since it is given that the field is an equilateral triangle, all its sides are equal.

Therefore 3*sides = 2490 Meters: side = 2490/3 = 830Meters

Since it will be difficult to construct a triangle of side = 830 meters, we can use the scale of 100meters = 1cm to construct the triangle. We need to construct an equilateral triangle with side = 8.3cm.

Since all the sides of an equilateral triangle are same, we need to construct a triangle with sides 8.3cm, 8.3cm and 8.3cm.

Exercise: Follow the method described in 6.4.2 problem 1(above) to construct the triangle.

6.4.2.2. Construction of a triangle when 2 sides and an included angle are given

6.4.2 Problem 3: Construct a triangle ABC with AB = 3cm, BC = 4cm and ABC =120⁰

Method:

First draw a rough figure of the triangle ABC

No	Steps
1	Draw a line and mark a point A, on that line
2	With A as center, cut an arc of radius 3cm to cut the above line at B(AB=3cm)
3	Use protractor to mark a point whose angle is 120⁰ from B
4	Draw a line from B passing through the above point
5	With B as center, cut an arc of radius 4cm to cut the above line at C
6	Join AC : ABC is the required triangle

Note: The above method is used for constructing a right angled triangle with 2 sides given.

6.4.3 Congruency of Triangles

You must have seen ponds. Have you ever thought of finding the width of the pond without getting into the water?

Similarly will it be possible to find the width of a river without getting into water?

Geometry helps us in solving such problems which we encounter in our daily life.

If you look in a dictionary, we find that congruence means equivalence, resemblance, similarity, etc. In geometry we say that,

two figures are congruent if they have similar properties (i.e. when we super impose one figure over the other, they fit in exactly without variations).


2 Lines are congruent if they are of equal lengths	2 Angles are congruent if they are equal measure in degrees	The ‘corresponding sides’ are the sides opposite to the angle which are equal in two triangles (In the above figure, AC and DF,AB and EF, BC and DE are corresponding sides) The ‘corresponding angles’ are the angles opposite to the sides which are equal in two triangles. (In the above figure, ABC and DEF, ACB and EDF, BAC and DFE are corresponding angles) Two Triangles are said to be ‘congruent’ if the corresponding three sides and three angles of both triangles are equal.
AB=CD=3cms	ABC =FDE = 60⁰	AC=DF,AB=EF, BC=ED, CAB =EFDABC=DEF,ACB=EDF
The symbol for congruence is
ABCD	ABCFDE	ABCDEF

Observation: Two congruent triangles have equal area because they fit in exactly when superimposed.

6.4.3 Example 1: Though a triangle has 6 elements (3 sides and 3 angles) let us construct the below mentioned triangles (ABC)

with the following three elements (data).

1. BC = 4cm, CA = 4.5cm, BA= 5cm

2. BC = 4cm, ABC =40⁰, BCA =50⁰

3. BC = 5cm, CA=7cm, BCA = 35⁰

4. The angles of the triangle are 60⁰, 50⁰, 70⁰

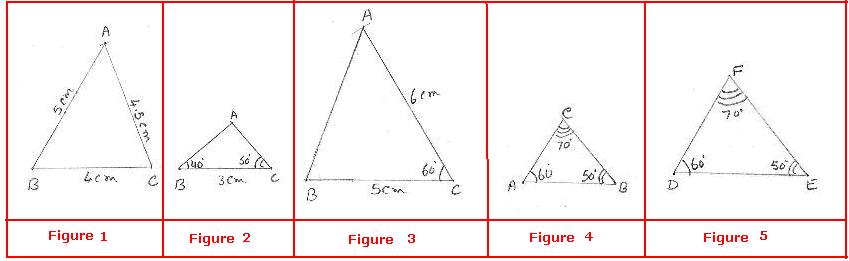
Note that when we are given only three angles, we can construct several triangles.

(In Figure 4 and Figure 5, although the corresponding angles are same, AB DE, BC FE and AC DF)

Conclusion: With the following three elements we can construct unique triangles

1. Length of three sides

2. Two angles and length of one side

3. Length of two sides and the included angle

Note: Given, length of two sides and an angle other their included angle we can not construct a unique triangle.

In the adjacent figure, length AB and AC are given and also the angle BAC.

Extend AC and let D be a point on this extended line such that BC =BD.

We observe that with the given data, we have drawn two triangles ABC and ABD (AB as common side

and BAC as common angle).

Table A: In general we can tabulate our findings as follows:

Side	Side	Side	Angle	Angle	Angle	Result
Y	Y	Y	-	-	-	We can construct triangle uniquely
Y	-	-	Y	Y	-	We can construct triangle uniquely
Y	Y	-	Y	-	-	We can construct triangle uniquely (if the angle is included angle)
-	-	-	Y	Y	Y	Several triangles can be constructed

Note: If 2 angles are given, the third angle can easily be found as the sum of 3 angles in a triangle is 180⁰.

Observation: As per the definition of congruency, for congruence, all the corresponding 3 sides and 3 angles of two triangles have to be equal.

But we have seen that, to draw a unique triangle we do not need to know all the 6 elements (length of all the 3 sides and all the 3 angles).

We have concluded that we need a maximum of three elements. We have also found out these combinations (Table A).

We have seen that it is possible to construct a triangle, if length of two sides and the included angle are given. We conclude that

‘Two triangles are congruent if two sides and included angle of one triangle are equal to the corresponding sides and included angle of the other triangle’.

This statement is called ‘SAS (Side, Angle, and Side) Postulate on congruence’.

6.4.3 Problem 1: To Measure width of a pond

Find the width of the pond given in the figure.

Solution:

Step: Have 2 poles (at A, B) on the edges of the pond, where you want to find the width.

Have another pole (at C) on the ground in front of the pond, which is visible to both A and B.

Extend AC to E such that AC=CE and BC to D such that BC=CD.

ACB = DCE (vertically opposite Angles)

By the above SAS postulate we conclude that the Triangles ABC and DEC are congruent.

Hence AB=DE

Measure distance DE to know the width of the pond.

6.4.3 Problem 2: In the adjoining figure PQRS is square. M is the middle point of PQ.

Prove that SM=RM

Solution:

Since PQRS is square, PS=QR, SPQ =90⁰ & PQR = 90⁰(so SPQ = PQR )

Since M is the middle point of PQ, PM=MQ.

So we have two triangles SPM and MQR whose 2 sides and the included angles are equal.

Therefore SPM MQR and hence their 3^rd sides (SM, MR) are equal.

Activity: Construct a triangle of AB=4cm and AC=BC=5cm (2 sides are equal).

Measure the angles CAB and ABC.

Do you notice that CAB =ABC?

Observations: In a triangle, angles opposite to equal sides are equal.

Let us prove this mathematically.

6.4.3 Base Angle Theorem:

The angles opposite to equal sides of a triangle are equal.

Data: In the adjoining triangle ABC, AC=BC

To prove CAB= ABC

Construction: Bisect the angle ACB such that the bisector line CD meets AB at point D.

Steps	Statement	Reason
1	AC=BC	This is the given data (equal sides)
2	ACD=DCB	CD is bisector of the angle ACB
3	CD is the common side of triangle ACD and DCB	our construction
4	Triangles ACD & DCB are congruent	SAS Postulate (2 sides and included angles are equal)
5	CAB= ABC	Corresponding angles of congruent triangles

This proves the theorem.

6.4.3 Problem 3: In the adjoining figure AB=AC. L and M are points on AB and AC such that AL=AM. Prove that ALM =AML.

Also prove that ABM ACL and LCB MBC, LM||BC

Solution:

Steps	Statement	Reason
1	AL=AM	given
2	BL = CM	AB=AC and AL=AM(given)
3	ALM =LMA	The angles opposite to equal sides(AL,AM) of a triangle are equal (Base Angle theorem)
4	AB=AC	Given.
5	BAM is common to both ABM and ACL
6	ABM ACL	SAS postulate (step1,step5,step4)
7	ABC =BCA	Base angle theorem(AB=AC)
8	LB=CM	Step1,2,3
9	BC is common base to both LCB and MBC
10	LCB MBC	SAS postulate (step2,step7,step9)
11	2ALM = 180⁰-LAM	ALM+LMA+LAM = 180⁰ and ALM = LMA
12	2ABC = 180⁰-LAM	ABC+BCA+LAM = 180⁰ and ABC = BCA
13	ALM = ABC	Step 11 and 12 as RHS of both are same
14	LM \|\|BC	Corresponding angles are equal (Step 13)

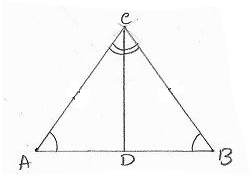
Activity: Construct few pairs of triangles such that, two angles (say 30⁰,50⁰) on the common side of one triangle are equal to

other triangles. Did you notice that the lengths of opposite sides are equal in all the cases?

6.4.3 Converse of Base Angle Theorem: In a triangle, the sides which are opposite to equal angles are equal.

Data: In the adjoining triangle ABC, CAB= ABC

To prove: AC=BC

Construction: Bisect the angle ACB such that the bisector line CD meets AB at point D.

Steps	Statement	Reason
1	CAB= ABC	This is the given data (equal sides)
2	CD is the common side of triangle ACD and DCB	our construction
3	ACD =DCB	Construction (bisector of ACB)
4	ACD DCB	ASA Postulate
5	AC=BC	Corresponding sides of congruent triangles

This proves the Converse of the base angle theorem.

6.4.3 Problem 4: Prove that in an isosceles triangle, the angular bisector of vertex angle bisects the base and is perpendicular to the base.

Solution:

Data: In the adjoining triangle ABC, AC=BC

To prove: AD=DB and ADC =CDB = 90⁰

Construction: Bisect the angle ACB so that the bisector line CD meets AB at point D.

Steps	Statement	Reason
1	AC=BC	This is the given data (equal sides)
2	ACD = BCD	our construction
3	CD is the common side of triangle ACD and DCB	our construction
4	Triangles ACD & DCB are congruent	SAS Postulate (2 sides and included angles are equal)
5	AD=DB	In a congruent triangle corresponding sides are equal
6	ADC = CDB	In a congruent triangle corresponding angles are equal
7	ADC+CDB=180⁰	Two angles are on a straight line
8	ADC =CDB = 90⁰

Activity: Construct few pairs of triangles such that the sides of a triangle (say 4cm,5cm,6cm) are equal to the sides of other triangles.

Did you notice that they are all congruent?

We have seen that it is possible to construct a triangle if lengths of all the 3 sides are given. We conclude that

‘Two triangles are congruent if the sides of one triangle are equal to the corresponding sides of another triangle’.

This statement is called ‘SSS (Side, Side, Side) Postulate

on congruence’.

6.4.3 Problem 5: PQRS is a square. A, B, C, D are mid points of PQ, QR, RS and SP respectively. Prove that BAC=BCA.

Solution:

Since PQ=SR and A and C are mid points of PQ and SR, we have AQ=CR.

Since B is mid point of QR, we have QB=BR.

Since PQRS is square AQB=90⁰ =BRC

So we have 2 triangles, AQB and CRB, whose 2 sides are equal and included angles are also equal.

By SAS postulate they are congruent and hence AB=BC and CAB is an isosceles triangle.

Thus by base angle theorem, angles opposite to equal sides are equal.

Hence BAC=BCA

Activity: Construct few pairs of triangles such that 2 angles and their common side (say 60⁰,70⁰, 4cm) are equal to 2 angles and

the common side of other triangles. Did you notice that they are all congruent?

We have seen that it is possible to construct a triangle if two angles and length of their common side are given. We conclude that

‘Two triangles are congruent if two angles and common side of one triangle are equal to the corresponding angles and common side of another triangle’.

This statement is called ‘ASA (Angle, Side, Angle) Postulate on congruence’.

Corollary: (corollary means consequence, outcome…) “Two triangles are congruent if two angles and any one side of one triangle are equal

to corresponding 2 angles and corresponding side of another triangle”. This statement is called ‘AAS (Angle, Angle, Side ) Condition

on congruence’.

Proof:

1. Sum of all the angles in a triangle =180⁰

2. Given 2 angles of a triangle, we can arrive at the third angle of triangle (=180⁰ – sum of given 2 angles)

3. Any 2 of the 3 angles can become the angles on the given common side.

Since two triangles have corresponding angles equal and common sides equal, by ASA postulate, these triangles are congruent.

6.4.3 Converse of Base Angle Theorem: In a triangle, the sides which are opposite to equal angles are equal.

Data: In the adjoining triangle ABC, CAB= ABC

To prove: AC=BC

Construction: Bisect the angle ACB such that the bisector line CD meets AB at point D.

6.4.3 Problem 6: To Measure width of river

Solution:

Identify a fixed object such as tree (B) on the other side of river. Erect a pole at A (opposite to B)

on your side, such that BA is a straight line. Erect a pole at some distance from A at C.

Erect another pole at D such that AC=CD (C is mid point of AD). Erect another pole at E

such that DE is perpendicular to AD and points B,C and E lie on a straight line.

We notice the following:

1. BAC = 90⁰= CDE (BA and DE are constructed perpendicular to AD).

2. ACB = DCE (Vertically opposite angles)

3. AC=CD (By construction)

Thus 2 angles and their common side in BAC and EDC are equal.

By ASA postulate,BAC EDC. Thus BA=DE.

By measuring DE we get the width of river without getting into water.

6.4.3 Problem 7: In the adjoining figure AC Bisects DF and EDC =AFE. Prove that AE=EC

Solution:

In the given figureAEF =DEC (opposite angle)

DE=EF & EDC =AFE (given data)

Therefore by ASA postulate, AEF and DEC are congruent triangles.

AE=EC.

Table: Postulates for congruency of triangles:

Side	Side	Side	Angle	Angle	Angle	Postulate
Y	Y	Y	-	-	-	SSS
Y	-	-	Y	Y	-	ASA
Y	Y	-	Y	-	-	SAS

Note that for congruency of triangles, at least one side has to be equal.

6.4.3 Exercise : Use these postulates to prove that your method of construction of following is correct(Refer 6.1)

1. Construction of an angular bisector

2. Construction of a perpendicular line at a point on a line(Perpendicular bisector Theorem)

3. Construction of a perpendicular bisector of a line

6.4.3 Theorem: Two right angled triangles are congruent if the hypotenuse and a side of one triangle are equal to the hypotenuse and the

corresponding side of the other triangle.

Data: ABC and DEF are given right angled triangles (ABC =DEF= 90⁰) and AB=DE, AC=DF

To prove: ABC DEF

Construction: produce FE to the point G such that GE=BC and join DG.

Steps	Statement	Reason
1	AB=DE	Given data
2	ABC =DEF= 90⁰	Given data
3	ABC =DEG = 90⁰	Construction and DEG+DEF = 180⁰
4	BC=GE	construction
5	ABC DEG	SAS postulate(step1,step3,step4)
6	ACB=DGE	Corresponding angles
7	DG=AC	Corresponding sides
8	AC=DF	Given data
9	DG=DF	step7,step8
10	DE is common to DEF and DEG	Construction
11	DEG = DEF = 90⁰	Construction
12	DFE = DGE	Base angle theorem forGDF
13	GDE = EDF	Sum of 3 angles in a triangle =180⁰ GDE =180⁰–DEG-DGE =180⁰–DEF -DFE(step2,step3,step12) = EDF
14	DEG DEF	ASA (step 13,step10,step11)
15	ABC DEF	Step 5,14

This is also called RHS (Right Angle, Hypotenuse, Side) Postulate on congruence.

6.4.3 Problem 8: If the three altitudes of a triangle are equal, prove that it is an equilateral triangle.

Solution:

The perpendicular drawn from a vertex of a triangle to its opposite side is called altitude.

In the adjoining figure EC,BF,AD are altitudes

Steps	Statement	Reason
1	Consider the BEC and BFC
2	EC=BF	Equal altitudes(given)
3	BEC=BFC = 90⁰	BE and BF are Altitudes
4	BC is common
5	BEC BFC	RHS postulate
6	ABC = BCA	Corresponding angles
7	Consider the ADB and ADC
8	ADB=ADC = 90⁰	AD is Altitude
9	AD is common
10	ABC = BCA	Step 6
11	ADB ADC	ASA postulate
12	AB =AC	Corresponding sides are equal
13	BC= AC	Similarly we can prove BFC BFA
14	AB=AC=BC	Step 12,13

6.4 Summary of learning

No	Points to remember
1	In any triangle sum of the three angles is 180⁰
2	If one of the sides of a triangle is extended, the exterior angle so formed is equal to the sum of interior opposite angles
3	Two Triangles are congruent if the corresponding three sides and three angles of both triangles are equal
4	SAS Postulate
5	The angles opposite to equal sides of a triangle are equal (Base angle theorem) and converse of this is also true
6	SSS Postulate
7	ASA Postulate

Additional Points:

More constructions of triangles:

6.4.2 3. Construction of a triangle when two angles and included side(base) are given

6.4.2 Problem 4: Construct a triangle ABC with ABC = 40⁰, BCA = 50⁰ and BC = 3cm

1. First draw a rough figure of the triangle ABC.

2. Draw the line BC=3cm

3. At B and C draw lines at 40⁰ and 50⁰ to base BC and let these lines meet at A

4. ABC is the required triangle

6.4.2 4. Construction of a right angled triangle when lengths of one side and hypotenuse are given

6.4.2 Problem 5: Construct a right angled triangle with base of length 3cm and hypotenuse of length 5cm.

1. First draw a rough figure of the triangle ABC.

2. Draw the line BC=3cm

3. Draw a perpendicular at B

4. From C draw an arc of radius 5cm to cut the perpendicular at A

5. ABC is the required triangle

6.4.2 5. Construction of an isosceles triangle when its base and altitude (height) are given

6.4.2 Problem 6: Construct an isosceles triangle ABC with base AB = 6cm and altitude = 4cm.

Here, we use the property of an isosceles triangle which states that

the altitude bisects the base.

1. First draw a rough figure of the triangle ABC.

2. Draw the base AB = 6cm

3. Bisect AB at D (AD=DB=3cm)

3. Draw a perpendicular at D above AB

4. From D draw an arc of radius 4cm to cut this perpendicular at C

5. ABC is the required triangle

6.4.2 6. Construction of an isosceles triangle when its altitude and angle of vertex are given

6.4.2 Problem 7: Construct an isosceles triangle with altitude = 4.5cm and angle at vertex = 50⁰

Here, we use the property of an isosceles triangle which states that, the altitude bisects the angle at vertex.

1. First draw a rough figure of the triangle ABC.

2. Draw a base line

3. Chose any point D on this line

4. Draw perpendicular at D above the base line

4. From D draw an arc of radius 4.5cm to cut this perpendicular at C

5. Draw lines making an angle of 25⁰ with CD, on both sides of DC and let these lines cut the base line at A and B

6. ABC is the required triangle

6.4.2 7. Construction of an equilateral triangle when its altitude is given

6.4.2 Problem 8: Construct an equilateral triangle whose altitude = 4.5cm

Here, we use the property of an equilateral triangle which states that, each angle in an equilateral triangle is 60⁰.

This construction is equivalent to the construction 6.4.2.6 with angle at vertex = 60⁰.

6.4.2.8. Construction of an isosceles triangle when its base and base angle is given

(Since base angles of an isosceles triangle are equal, this construction is equivalent to the construction as given in 6.4.2.3)

6.4.2.9. Construction of an equilateral triangle when its one side is given

(Since all sides of an equilateral triangle are equal, this construction is equivalent to the construction when all the 3 sides of a triangle are given as in 6.4.2.1)

6.4.3 Perpendicular bisector Theorem:

1. Every point on the perpendicular bisector is equidistant from the two given points.

2. Any point which is equidistant from the two given points, lies on the perpendicular bisector of the line joining these 2 points.

In the adjacent figure YLX is the perpendicular bisector of AB (i.e. AL = LB and ALY = 90⁰)

We are required to prove that,

1. If point P is on YLX then AP=BP

2. If P is a point such that AP=BP then P lies on the line XLY

Hint:

Part 1:

If point P is L itself then it is obvious that AP=PB

If point is not L then join AP and PB

Use SAS postulate to prove that ALP BLP (hence AP=BP)

This proves the first part of the theorem.

Part 2:

If point P is L itself then P lies on XLY

If point P is not L then join AP and PB

Use SSS postulate to prove that ALP BLP (hence ALY =BLY = 90⁰)

LP is perpendicular to AB and hence P is on the perpendicular line XLY

This proves the second part of the theorem.

Note:

The locus of a point which is equidistant from two fixed points is the perpendicular bisector of the line segment joining the fixed points.

(Refer section 6.1 for definition of locus).

6.4.3 Angular bisector Theorem:

1. Every point on the anglular bisector is equidistant from the sides of the angles.

2. Any point which is equidistant from the sides of the angles lies on the bisector of the angle.

In the adjacent figure AR is the bisector of BAC (i.e. EAR = DAR)

We are required to prove that,

1. If point P is on AR then PE=PD

2. If P is a point on AR such that PE = PD then P lies on the line AR

Hint:

Draw PE and PD perpendicular to AC and AB respectively from P

Part 1:

Use ASA postulate to prove that APE APD (hence EP=DP)

This proves the first part of the theorem

Part 2:

Use RHS postulate to prove that APE APD (hence EAP =DAP)

This proves the second part of the theorem.

Note:

The locus of a point which is equidistant from two intersecting straight lines is the angular bisector of the angle made by these lines.

6.4.1 Observations:

1. The ratio of the areas of two triangles is equal to the ratio of the products of the base and it’s corresponding height, of those two triangles.

Proof:

Let ABC and DEF be the two triangles as shown in the adjoining figure.

We know that the area of a triangle = 1/2*Base*height

Area of ABC/Area of DEF

= (1/2) BC*AL/{(1/2) EF*DM}

= BC*AL/{EF*DM}

Based on the above observation, prove the following:

2. Triangles of equal heights have areas proportional to their corresponding bases.

3. Triangles of equal bases have areas proportional to their corresponding heights.

Inequalities: (Proof not provided for the following theorems)

Theorem 1: If two sides of a triangle are not equal, then the angle opposite to the greater side is greater than the angle opposite

to the smaller side.

In the adjoining figure BCA > ABC

Theorem 2: If two angles of a triangle are not equal, then the side opposite to the greater angle is greater than the side opposite to the smaller angle.

In the adjoining figure AB > BC

Corollaries:

1. The sum of lengths of any two sides of a triangle is always greater than the third side

(Ex. AC+BC>AB)

2. The difference between the lengths of any two sides of a triangle is always less than the third side

(Ex. AB-AC < BC)

3. Among all the line segments joining a point outside a given line and any point on the line, the

perpendicular line segment is the shortest.