

















6.8 Parallelogram:
6.8.1
Construction of parallelogram
We have seen earlier (6.7.1) that
to construct unique quadrilaterals, we require five elements
- a suitable combination of sides, diagonals
and angles as given below
|
No. |
No of sides given |
Number of diagonals given |
Number of angles given |
Total Number of elements required |
|
1 |
2 |
2 |
1 |
5 |
|
2 |
2 |
1 |
2 |
5 |
|
3 |
4 |
1 |
- |
5 |
|
4 |
4 |
- |
1 |
5 |
|
5 |
3 |
- |
2(Included) |
5 |
|
6 |
3 |
2 |
- |
5 |
|
7 |
2(Adjacent) |
- |
3 |
5 |
Since parallelogram has a special
property of opposite sides being parallel and opposite angles being equal,
we just need three elements to construct a unique parallelogram as
given below
|
No. |
No of sides given |
Number of diagonal given |
Number of angles given |
Total Number of elements required |
|
1 |
2 |
1 |
- |
3 |
|
2 |
2 |
- |
1 |
3 |
|
3 |
- |
2 |
1(Intersecting ) |
3 |
|
4 |
1 |
2 |
- |
3 |
6.8.1.1 Construction of
a parallelogram given the length of 2 adjacent sides and a diagonal.
In a parallelogram, opposite sides
are equal. If lengths of 2 adjacent sides are given, we can arrive at the
lengths of all sides.
Thus, the construction is similar to that of a
quadrilateral with 4 sides and 1 diagonal given
(Refer 6.6.1).
|
6.8.1 Exercise 1: Construct a parallelogram whose adjacent sides
are 5cm and 3cm and diagonal is 6cm. (The sides are 5cm, 3cm, 5cm and
3cm and diagonal is 6cm) |
|
6.8.1.2. Construction
of a parallelogram given the length of 2 adjacent sides and an angle.
In a parallelogram, opposite sides
are equal. If lengths of 2 adjacent sides are given, we can arrive at the
lengths of all sides.
Thus, the construction is similar to that of a
quadrilateral with 4 sides and 1 angle given (Refer
6.6.1).
|
6.8.1 Exercise 2: Construct a parallelogram PQRS, given PQ=5cm,
QR=4cm and (The sides are PQ=5cm, QR=4cm,
RS=5cm and PS=4cm and |
|
6.8.1.3. Construction
of a parallelogram given the length of two diagonals and intersecting angles
between them.
6.8.1 Problem 1: Construct a
parallelogram whose diagonals are 4cm and 5cm and the angle between them is =
700.
First draw a rough diagram of ABCD
with AC and BD as diagonals.
|
Step |
Construction |
|
|
1 |
Mark a point A and draw a line
though A |
|
|
2 |
From A, draw an arc of radius
4cm to cut the above line at C
(AC=4cm) |
|
|
3 |
Bisect AC at O (From A and C, draw arcs of
radius more than half the length of AC on both sides, Let they cut at X and Y.
XY is the perpendicular bisector of AC. It cuts AC at O |
|
|
4 |
From O, draw a line at an angle
700 to AC on both sides |
|
|
5 |
From O, draw an arc of radius
2.5cm on both sides of AC to cut the above line at B and D. Join AB, BC, CD
and DA. |
ABCD
is the required parallelogram.
6.8.1.4. Construction
of a parallelogram given the length of one side and two diagonals.
With the given side as
the base, construct a triangle (with half of diagonals as other two sides) by
using the property that diagonals of a
parallelogram bisects each other.
Then extend these other two sides.
|
6.8.1 Exercise 3: Construct a parallelogram ABCD with BC=4.5cm and diagonals
AC=4cm and BD=5.0cm. In the figure of 6.8.1 Problem 1
use the property AO=OC and BO=OD to construct triangle BCO with BC= 4.5cm,
CO=2cm and BO=2.5cm and then extend CO and BO such that OA = 2cm and
OD=2.5cm. Join CD,DA,AB |
|
6.8.1.5. Construction
of a parallelogram given the length of adjacent sides and the height of
parallelogram.
6.8.1
Exercise 4: Construct a parallelogram ABCD,
with adjacent sides AB=4 cm, BC = 5cm and height corresponding to BC =3.5 cm
|
Step |
Construction |
|
|
1 |
Mark a point B and draw a line
though B |
|
|
2 |
From B, draw an arc of radius
5cm to cut the above line at C (Hence BC=5cm) |
|
|
3 |
Draw 2 perpendicular lines XY
and PQ on BC at any two points U and T
on it. |
|
|
4 |
From U and T cut PQ and XY at S and R by an arc of radius 3.5 cm Join RS ( Note RS is at a
distance of 3.5cm from BC) |
|
|
5 |
Cut the line RS at A by an arc
of radius 4cm from B (Hence BA=4cm) |
|
|
6 |
From A cut the line RS at D by
an arc of radius 5cm ( Hence AD=5cm) |
ABCD
is the required parallelogram.
6.8.2
Area of parallelogram
|
ABCD is a parallelogram with
AB||CD, BC||AD and AB=CD, AD=BC. From D and C draw perpendiculars
to AB (extend if necessary). Let them meet AB at E and F. DE and CF are the altitudes of
the parallelogram. Since AB||CD, altitudes are equal (DE=CF). The triangles ( and hence AE=BF and hence Area
of
= Area of = DC * h Area of the
parallelogram = base*height |
|
6.8.2 Problem 1: ABCD is a parallelogram
with AB=24cm and AD=16cm. The distance between AB and DC is 10cm. Find the
distance between AD and BC.
Solution:
|
The distance between AB and DC
is the height (DE). Area of the parallelogram ABCD =
base*height = 24*10 = 240sq cm This is also the area of the
same parallelogram with AD as the base and AH as the height.
But area = 240sqcm
I.e. AH = 240/16 = 15cm |
|
6.8.2 Problem 2: A rectangle and a
parallelogram have equal areas. The sides of the rectangle are 10m and 14m.
The base of the parallelogram is
20m. What is the altitude of the parallelogram?
Solution:
|
We know that the Area of
rectangle = side*side = 10*14 = 140sqm Area of parallelogram = Base*Altitude
= 20*Altitude Since both the areas are same Area of parallelogram =140sqm
i.e. Altitude = 140/20 = 7mts |
|
6.8.2 Problem 3: A triangle and a
parallelogram have equal areas and equal bases. What is the ratio of their
altitudes?
Solution:
|
If BP and HP
are base and altitude of the parallelogram, then the area of parallelogram = Base
*Altitude = Bp*Hp If BT and HT
are base and altitude of the triangle, then the area of triangle = 1/2(Base *Altitude) = 1/2(BT*HT). Since the areas are same, Bp*Hp=1/2(BT*HT).
Since the bases are same, BP=
BT. We have Hp=1/2HT i.e. 2Hp=HT Therefore the altitude of the
triangle is twice the altitude of the parallelogram. |
|
6.8.2 Problem 3: Have you observed your
mother, grandmother or those who make sweets cutting .Burfis in the
shape of parallelogram than rectangles?
(Did they
study geometry?)

|
For
example let the sides of rectangle and parallelogram be 13 and 12 units. Area
of rectangle = base * another side = 12*13= 156 square units Area
of parallelogram = base * height =
12*12= 154 square units (
we used the pythogoras theorem to find the height of parallelogram (122= 132-52) Thus
we notice that area of parallelogram
< area of rectangle |
|
Though the sides of rectangle and parallelogram are
same, area of rectangle is more than the area of parallelogram. Hence in the
same spread (area)
they can cut more number of
pieces in the shape of parallelograms than in the shape of rectangles.
6.8.3
Construction of Rhombus:
We have seen that, to construct a
parallelogram we need three elements (suitable combination of sides, diagonals
and angles).
Because of the special property of
rhombus, only two elements are enough to construct a rhombus uniquely.
1. Length of two
diagonals are given .
6.8.3 Problem 1: Construct a rhombus PQRS with PR
= 5cm and SQ=4cm
First draw a rough diagram
|
Step |
Construction |
|
|
1 |
Mark a point P and draw a line
though P |
|
|
2 |
Draw an arc of radius 5cm to cut
the above line at R (PR=5cm) |
|
|
3 |
Bisect PR at O (From P and R, draw arcs of
radius more than half the length of PR, on both sides of PR. Let they cut at X and Y. (XY is the perpendicular
bisector of PR) |
|
|
4 |
From O draw an arc of radius 2cm
to cut OX at S(OS=2cm) |
|
|
5 |
From O draw an arc of radius 2cm
to cut OY at Q(OQ=2cm). Join PQ, QR, RS and SP. |
PQRS
is the required rhombus.
2. Lengths of one side
and one diagonal are given
6.8.3 Problem 2: Construct a rhombus ABCD with AB
= 3cm and AC=4cm
First draw a rough diagram
|
Step |
Construction |
|
|
1 |
Mark a point A and draw a line
though A |
|
|
2 |
Draw an arc of radius 4cm to cut
the above line at C (AC=4cm) |
|
|
3 |
From A, draw arcs of radius 3cm
on both sides of AC |
|
|
4 |
From C, draw arcs of radius 3cm
on both sides of AC to cut the above arcs at D and
B. Join AB, BC, CD and DA. |
ABCD
is the required rhombus
3. Lengths of one side
and one angle are given
6.8.3 Problem 3: Construct a rhombus ABCD with AB
= 3cm and ![]() ABC = 1200.
ABC = 1200.
First draw a rough diagram
|
Step |
Construction |
|
|
1 |
Mark a point B and draw a line
though B |
|
|
2 |
Draw a line through B at an angle of 1200 with BC |
|
|
3 |
From B, draw an arc of radius
3cm to cut the above line at A (BA=3cm and |
|
|
4 |
From A and C, draw arcs of
radius 3cm to meet at D. Join AD and DC. |
ABCD
is the required rhombus
6.8.4
Area of Rhombus:
|
We have seen(in 6.6) that a
diagonal of a rhombus cuts the rhombus into 2
congruent triangles. We shall use this property to
calculate the area of rhombus, as we already know how to calculate the area of a
triangle. In the rhombus PQRS, draw the
diagonal PR and QS. As PQRS is a
rhombus, diagonals bisect each other perpendicularly ( OS and OQ are the altitudes of Area of Area of
= 1/2(PR*OS) + 1/2(PR*OQ) =
1/2*PR* (OS+OQ) =1/2*PR*QS sq units Area of a rhombus = ½ *
product of diagonals |
|
Note : This formula was also
given by Bhaskracharya (Lilaviti Shloka 176)
6.8.4 Problem 1: The longer diagonal of
a rhombus is greater than the other diagonal by 10mts. The sum of diagonals is
32mts. Find its area.
Solution:
|
Let the shorter diagonal be x. Since the longer diagonal is
greater than the other diagonal by 10mts, its length will be x+10. Since the sum of diagonals is 32m. We have x+(x+10) = 32 i.e. 2x+10 =32 i.e. 2x=32-10 =22
Hence its diagonals are 11 and 21(=11+10)
meters. We know that Area of a rhombus = 1/2
* product of diagonals = 1/2*11*21 = 231/2 sq mts |
|
6.8.4 Problem 2: The perimeter of a rhombus is
40cm and one of its diagonal is 16cm. Find the other diagonal and area of
rhombus.
Solution:
|
Let x be the side. Since perimeter
is sum of all sides and all sides are equal in a rhombus: We have 4x = 40cm
Thus in As PQRS is a rhombus, diagonals
bisect each other perpendicularly ( PR=16cm(given)
POQ is a right angled triangle
with PQ=10 and By Pythagoras theorem PQ2= PO2+OQ2
Since OQ=OS, we have OS=6cm and
hence QS =6+6=12cm Area = 1/2* product of diagonals
= 1/2* 16*12= 96 sq cms |
|
6.8.5
Construction of Trapezium:
Trapezium can be thought of as a figure
got by merging a triangle with parallelogram.
We have seen that to construct a
quadrilateral we require five elements. Since trapezium has one pair of opposite
sides parallel,
we require a maximum of four
elements to construct a trapezium uniquely.
6.8.5.1. When length of two sides and two angles are given
6.8.5 Problem 1: Construct a trapezium ABCD with
AB||CD, AB=5cm, CD=3cm and (![]() DAB = 700
DAB = 700 ![]() ABC = 500)
ABC = 500)
First draw a rough diagram.
|
Step |
Construction |
|
|
1 |
Mark a point A and draw a line
though A |
|
|
2 |
From A, draw an arc of radius
5cm to cut the above line at B (AB=5cm) |
|
|
3 |
From A, draw an arc of radius
2cm (=AB-CD) to cut AB at E (AE=2cm) |
|
|
4 |
Draw a line through A at an
angle of 700 to AB |
|
|
5 |
Draw a line through E at an
angle of 500 to AB to cut
the above line at D |
|
|
6 |
Draw a line through B at an
angle of 500 to AB. |
|
|
7 |
From D, draw an arc of radius
3cm to cut the above line at C (DC=3cm and |
ABCD
is the required trapezium.
Note: In step 4, we used the
property of corresponding angles being equal when a transversal cuts two
parallel lines (
6.8.5. 2. When lengths of parallel sides and the altitude are
given.
6.8.5 Problem 2: Construct a trapezium PQRS with
PQ||SR, PQ=5cm, SR=6cm and PS=3cm
First draw a rough diagram.
|
Step |
Construction |
|
|
1 |
Mark a point P and draw a line
though P |
|
|
2 |
From P, draw an arc of radius
5cm to cut the above line at Q (PQ=5cm) |
|
|
3 |
Draw a perpendicular from P (altitudes
form 900) |
|
|
4 |
From P, draw an arc of radius
3cm to cut the above line at S (PS=3cm) |
|
|
5 |
Draw a perpendicular from S (parallel
to PQ) |
|
|
6 |
From S, draw an arc of radius 6cm
to cut the above line at R (SR=6cm) |
6.8.5. 3. When lengths of all sides are given.
Since trapezium can be
thought of as consisting of a triangle and Parallelogram first construct a
triangle of three sides like what is explained in 6.8.5 Problem1.
|
6.8.5 Exercise 1: Construct a trapezium ABCD with AB||CD, AB=7cm,
DC=5cm, AD=2cm and BC= 2.5cm Hint: Draw a rough diagram as in the figure on the right
side. Mark E on AB such that AE=AB-CD Construct triangle AED such that
AD =2cm, DE =BC=2.5cm From B draw a line parallel to
ED and mark C such that BC=2.5cm, Join D and C ABCD is the required trapezium |
|
|
6.8.5 Problem 3: Construct an isosceles trapezium ABCD with
CD||AB, AB=7cm, AD=2cm and DC=5cm Since in an isosceles trapezium
non parallel sides are equal, we have BC=AD. Thus, we have to construct a
trapezium ABCD with four sides given (DA=2cm, AB=7cm, BC=2cm and
CD=5cm). Hint: As in 6.6.8 Problem 1,
first we need to construct a triangle AED with AE = AB-DC = 7-5 = 3cm 1. With AD=2cm (given), AE = 3cm
(construction) and DE = CB = 2cm (parallelogram), we should be able to
construct the triangle ADE. 2. From B, draw an arc of radius
2cm and from D draw an arc of radius 5cm to cut at point C. Join DC and CB. 3. ABCD is the isosceles
trapezium. |
|
6.8.6
Area of Trapezium:
|
ABCD is a trapezium with BC||AD
and AB=CD. Draw perpendiculars from A and D
to the base BC to cut BC at E and F respectively. Since BC and AD are parallel,
the altitudes AE and DF are equal (the distance between parallel lines are
always same) Note that AEFD is a rectangle.
Therefore EF =AD and hence EF = 1/2EF+1/2EF=1/2(EF+AD) Area of trapezium ABCD = Area of
= 1/2(base*height)+ (side*side)+
1/2(base*height) = 1/2(BE*height)+ (EF*height)+
1/2(FC*height) = (BE/2 + EF + FC/2)*height = (BE/2+(EF+AD)/2+FC/2)*height ( = 1/2(BE+EF+AD+FC)*height = 1/2(BE+EF+FC+AD)*height = 1/2(BC+AD)*height Area of trapezium =
half the product of height and sum of parallel sides |
|
6.8.6 Problem 1: The parallel sides of a trapezium
are in the ratio of 2:1. If the distance between the parallel sides is 6cm and
the area is 135 sq cm,
find the length of parallel sides.
Solution:
|
It is given that the height of
the trapezium is 6cm. Since parallel sides of the
trapezium are in the ratio of 2:1, let the sides be 2x and 1x. We know Area of trapezium = half the
product of height and sum of parallel sides = 1/2(6*(2x+x)) = 3*3x = 9x We are also given that the area
is 135sq cm
|
|
6.8.6 Problem 2: The area of a trapezium is 204sq
cm. Its altitude is 17cm and one of the parallel sides is 16cms. Find the other
side.
Solution:
|
Let x be the other side Area of trapezium = half the
product of height and sum of parallel sides = 1/2(17*(16+x)) We are given that the area is
204 sq cm
The other side is 8cm Verification Area of trapezium =
1/2*17*(16+8) = 17*12 = 204 sq cm which is as given in the problem. |
|
6.8.7 Theorems on parallelograms:
6.8.7 Theorem
1: The diagonals of a parallelogram
bisect each other.
Data: ABCD is a parallelogram. The
diagonals AC and BD meet at O.
To prove: AO=OC and BO=OD
Proof:
|
Steps |
Statement |
Reason |
|
|
1 |
AB = CD |
Opposite sides of parallelogram |
|
|
2 |
|
Alternate angles of AB||CD, AC is transversal |
|
|
3 |
|
Alternate angles of AB||CD, BD is transversal |
|
|
4 |
|
ASA Postulate |
|
|
5 |
AO=OC and BO=OD |
Corresponding sides of congruent triangles |
This proves that the diagonal of a
parallelogram bisect each other.
6.8.7 Theorem
2: Each diagonal divides a
parallelogram in to two congruent triangles.
Data: ABCD is a parallelogram, AC
is a diagonal
To prove: ![]() ABC
ABC ![]()
![]() ACD
ACD
Proof:
|
Steps |
Statement
|
Reason |
|
|
1 |
AB = CD |
Opposite sides of parallelogram |
|
|
2 |
BC = AD |
Opposite sides of parallelogram |
|
|
3 |
AC is common |
|
|
|
4 |
|
SSS Postulate |
This
proves that the diagonal divides the parallelogram in to two congruent
triangles.
Corollary means a result/effect of
a main event.
For example,
August 15th is
celebrated as the independence day of
for schools/colleges/offices.
The main event here is
Independence Day. Corollary to that is, it is a holiday.
Similarly, based on Theorems we
derive Corollaries.
6.8.7 Corollary 1:
In a parallelogram, if one angle is a right angle then it is a rectangle.
Given: ABCD is a parallelogram.
ABC = 900
To Show: ABCD is a rectangle
|
Steps |
Statement
|
Reason |
|
|
1 |
|
Given |
|
|
2 |
|
Sum of two consecutive angles is
1800 |
|
|
3 |
|
Substitution in step 2 for ABC |
|
|
4 |
|
Opposite angles of a
parallelogram |
|
|
5 |
|
|
|
|
6 |
|
Opposite angles of a
parallelogram |
|
|
7 |
|
|
Hence
ABCD is a rectangle
6.8.7 Corollary 2:
In a parallelogram, if all the sides are equal and all the angles are
equal, then it is a square.
Given: ABCD is a parallelogram and
AB=BC=CD=DA.
To Show: ABCD is a square
|
Steps |
Statement
|
Reason |
|
|
1 |
|
Sum of two consecutive angles is
1800 |
|
|
2 |
2 |
Given that all the angles are
equal |
|
|
3 |
|
|
|
|
4 |
|
Sum of two consecutive angles is
1800 |
|
|
5 |
2 |
Given that all the angles are
equal |
|
|
6 |
|
|
|
|
7 |
|
||
Since it is also given that all
sides are equal, ABCD is a square.
6.8.7 Corollary 3:
The diagonals of a square are equal and bisect each other
perpendicularly.
Given: ABCD is a square hence
AB=BC=CD=DA and ![]() ABC =
ABC =![]() BCD=
BCD=![]() CDA=
CDA=![]() DAC=900
DAC=900
To Show: AC=BD,AO=CO,BO=DO,![]() AOB=
AOB=![]() BOC = 90
BOC = 90
|
Steps |
Statement |
Reason |
|
|
|
Consider |
||
|
1 |
AB=CD |
In a square, all sides are equal |
|
|
2 |
BC is common |
|
|
|
3 |
|
In a square all angles are right angles |
|
|
4 |
|
SAS Postulate |
|
|
5 |
|
Corresponding sides are equal |
|
|
|
Consider |
||
|
6 |
AB=CD |
In a square, all sides are equal |
|
|
7 |
|
Alternate angles of AB||CD, BD is transversal |
|
|
8 |
|
Alternate angles of AB||CD, AC is transversal |
|
|
9 |
|
ASA Postulate |
|
|
10 |
|
Corresponding sides are equal |
|
|
|
Consider |
||
|
11 |
AB=BC |
In a square, all sides are equal |
|
|
12 |
AO=OC |
BO bisects AC (Step 9) |
|
|
13 |
BO is
common |
|
|
|
14 |
|
SSS Postulate |
|
|
15 |
|
Corresponding angles are equal |
|
|
16 |
|
Sum of angles on a straight line is 1800 |
|
|
17 |
2 |
|
|
|
18 |
|
(Step 15) |
|
Hence the diagonals of a square
bisect each other at right angles.
6.8.7 Corollary 4:
The straight line segments joining the extremities of two equal and
parallel line segments on the same side are equal and parallel.
Given: AB=CD and AB||DC and A is
joined with D and B is joined with C
To Show: AD=BC and AD||BC
Construction: join AC.
|
Steps |
Statement |
Reason |
|
|
1 |
AB=CD |
Given |
|
|
2 |
|
Alternate angles of AB||DC, AC is transversal |
|
|
3 |
AC is common |
|
|
|
4 |
|
SAS Postulate |
|
|
5 |
|
Corresponding sides are equal |
|
|
6 |
|
(Step 2) |
Since DAC and ACB are alternate
angles with respect to the lines AD and BC with AC as a transversal, AD||BC.
6.8.7 Problem 1: In the adjoining adjacent figure, ABCD is a
parallelogram. P is the mid point of BC. Prove that AB=BQ
Given: ABCD is a parallelogram
with P as mid point of BC
To Show: AB=BQ
|
Steps |
Statement
|
Reason |
|
|
1 |
BP = PC |
Given that P is mid point of BC |
|
|
2 |
|
Vertically opposite angles |
|
|
3 |
|
Alternate angles as AB||DC |
|
|
4 |
|
ASA Postulate |
|
|
5 |
BQ = DC |
Corresponding sides are equal |
|
|
6 |
DC = AB |
Opposite sides of parallelogram
are equal |
|
|
7 |
|
From 5 and 6 |
6.8.7 Problem 2: In the adjoining figure, the bisectors of angles of
a parallelogram ABCD enclose PQRS. Prove that PQRS is a rectangle.
Given: ABCD is a parallelogram.
AP, BP, CR and DR are the angular bisectors of angles A, B, C and D
respectively.
To Show: PQRS is a rectangle.
|
Steps |
Statement
|
Reason |
|
|
1 |
|
Sum of consecutive angles of a parallelogram =1800 |
|
|
2 |
|
AP is bisector of |
|
|
3 |
|
DR is bisector of |
|
|
4 |
|
Substituting values of angles in
Step 1, from 2 and 3 |
|
|
5 |
|
Sum of all angles in a triangle
( |
|
|
6 |
|
Transposition |
|
|
7 |
= 1800-900 =
900 |
Substitute value from step 4 |
|
|
8 |
|
Vertically opposite angles are
equal |
|
|
9 |
= 900 |
|
|
|
10 |
|
Consecutive angles in a
parallelogram |
|
|
11 |
1/2 |
|
|
|
12 |
|
AP bisects A and BP bisects B |
|
|
13 |
|
Sum of all angles in |
Similarly we can show that ![]() PQR=
PQR=![]() QRS=900
QRS=900
Hence PQRS is a rectangle.
6.8.7 Problem 3: PQRS is a parallelogram. PS is extended (produced)
to M so that SM = SR and MR is extended to meet PQ extended at N.
Prove that QN=QR.
Given: PQRS is a parallelogram.
SM=SR
To Show: QN=QR
|
Steps |
Statement
|
Reason |
|
|
1 |
|
SM=SR and hence SRM is an
isosceles triangle |
|
|
2 |
|
Corresponding angles(SR||PQ) |
|
|
3 |
|
Corresponding angles(PS||QR) |
|
|
4 |
|
Equating Step |
|
|
5 |
|
Corresponding angles(SR||PN) |
|
|
6 |
|
Since two angles in |
|
|
7 |
|
From Step4, Step1, Step5 |
|
|
8 |
|
From Step 6, we conclude that |
6.8.7 Problem 4: ABCD is a parallelogram. The bisectors of ![]() A and
A and ![]() B meet BC and AD at X and Y respectively. Prove that XY=CD.
B meet BC and AD at X and Y respectively. Prove that XY=CD.
Given: ABCD is a parallelogram. AX
bisects![]() A and BY bisects
A and BY bisects![]() B. Let AX and BY meet at O
B. Let AX and BY meet at O
To Show: XY=CD
Consider ![]() ABX and
ABX and ![]() AXY
AXY
Data : AD ||BC and hence AY||BX,
AB=CD,
|
Steps |
Statement
|
Reason |
|
|
1 |
|
Alternate angles AY||BX and AX
is transverse |
|
|
2 |
|
Alternate angles AY||BX and AX
is transverse |
|
|
|
Consider |
||
|
3 |
|
Sum of angles in step 1 and step
2 |
|
|
4 |
BY is common side |
|
|
|
5 |
|
Alternate angles AY||BX and BY
is transverse |
|
|
6 |
|
ASA Postulate |
|
|
7 |
AB =XY, AY=BX |
Corresponding sides, Step 6 |
|
|
8 |
XY =CD |
AB=CD(given), step 7 |
|
6.8.7 Problem 5: ABCD is a parallelogram with AB||CD. P is the mid
point of AB and CP bisects ![]() BCD. Prove that
BCD. Prove that ![]() CPD =900
CPD =900
|
Hint: If we can prove that 1. Note that PBC is an isosceles
triangle ( 2. Prove that ADP is an
isosceles triangle (AD=BC, AP=PB and PB=BC and hence AD=AP) 3. DP bisects 4. 5. 2( 6. |
|
6.8.7 Theorem 3: Parallelograms standing on the same
base and between same parallel lines have equal areas.
Data: ABCD and ABEF are two
parallelograms standing on the same base AB and between same parallel lines PQ
and RS
To prove: Area of ABCD = Area of
ABEF.
Proof:
|
Steps |
Statement |
Reason |
|
|
|
Consider |
||
|
1 |
AF = BE |
Opposite sides of ABEF. |
|
|
2 |
|
Corresponding angles of
AF||BE and AD||BC, PQ is transversal |
|
|
3 |
|
When two angles of triangles are equal, third angle also has to be
equal |
|
|
4 |
|
ASA Postulate |
|
|
5 |
Area of |
Congruent triangles have equal area. |
|
|
6 |
|
Adding area of quadrilateral DEBA to both sides. |
|
|
7 |
i.e. Area of FEBA = Area of ABCD |
If equals are added to equals, then the resulting sums are also
equal. |
|
This proves the theorem.
Note: Earlier we have seen that the
area of parallelogram is product of base and its altitude (height). Since PQ
and RS are parallel lines, the altitudes
of FEBA and ABCD are equal. Since
the parallelograms, FEBA and ABCD have the same base AB, it follows that the
parallelograms have same area.
6.8.7 Corollary 1:
Parallelograms standing on equal base and between same parallel lines
have equal areas.
|
Note: We know that the area of parallelogram is product of base and its
altitude (height)(Refer 6.8.2) Since PQ and RS are parallel
lines, the altitudes of EFGH and ABCD
are equal. Since the parallelograms, EFGH and
ABCD have equal bases (AB=EF), it follows that the
parallelograms have same area. |
|
6.8.7 Corollary 2:
If a parallelogram and a triangle stand on the same base and between
same parallel lines, then the area of triangle is half the
area of the parallelogram.
Note:
|
We know that the area of parallelogram
(ABCD) is product of its base and its
altitude (height) (=AB*h).*(Refer 6.8.2) We have also proved that diagonal
divides a parallelogram in to two congruent triangles (refer 6.8.7 Theorem 2)
= 2 *area of
=1/2( AB*h) = 1/2 base *height |
|
Note : So far we have been
using the formula for area of a triangle = 1/2 base *height, without proof.
In the process of
proving above corollary, we have also arrived at the formula for calculation
for the area of triangle.
6.8.7 Corollary 3:
Triangles standing on the same base and between same parallel lines are
equal in area.
|
We know that the area of a
triangle is half the product of its base and its altitude
= (1/2)*base*height = (1/2)*AB*h In addition, we know that the
distance (h) between any two parallel lines is always fixed. Hence
|
|
Note: We can also prove the above by
constructing two parallelograms one || AC and another ||BD with AB as common
base and using theorem 6.8.7
Theorem 3 and 6.8.7 Corollary 2.
6.8.7 Corollary 4:
Triangles standing on equal base and between same parallel lines are
equal in area.
(By formula, area of triangle is
half of its base and height).
6.8.7 Problem 6: In the given figure DE||BC, prove that the area of ![]() BOD = Area of
BOD = Area of ![]() COE
COE
Given: DE ||BC
To Show: Area of ![]() BOD= Area of
BOD= Area of ![]() COE
COE
|
Steps |
Statement
|
Reason |
|
|
1 |
Area of |
BC is the common base for both |
|
|
2 |
Area of =Area of |
The common area of triangle BOC
is subtracted from the areas of both
the triangles of Step 1 |
|
|
3 |
|
|
6.8.7 Problem 7: In the given figure, D and E are the points on the
sides AB and AC respectively, such that the area of![]() BCE = Area of
BCE = Area of![]() BCD.
BCD.
Show that DE||BC
Given: Area of ![]() BCE = Area of
BCE = Area of ![]() BCD
BCD
To Show: DE || BC
|
Steps |
Statement
|
Reason |
|
|
1 |
Area of 1/2 BC*altitude of |
Formula for area of the triangle
with BC as base |
|
|
2 |
Area of 1/2 BC*altitude of |
Formula for area of the triangle
with BC as base (BC is common base) |
|
|
3 |
BC*altitude of |
It is given that areas of both
the triangles are same |
|
|
4 |
Altitude of Altitude of |
From step 3 |
|
|
5 |
DE || BC |
Distance between two lines are
same |
6.8.7
Data: In triangle ABC, D and E are
mid points of AB and AC respectively
To prove: DE||BC and DE=1/2BC.
Construction: From C, draw a line parallel
to AB. Extend DE to meet this line at F
Proof :
|
Steps |
Statement
|
Reason |
|
|
|
Consider |
||
|
1 |
AE = CE |
E is midpoint of AC |
|
|
2 |
|
Alternate angles of AB||CF |
|
|
3 |
|
Vertically opposite angles |
|
|
4 |
|
ASA Postulate |
|
|
5 |
DE=EF,AD=CF |
Corresponding sides are equal |
|
|
6 |
AD=DB |
Given that D is midpoint of BA |
|
|
7 |
|
From step 5 and step 6 |
|
|
8 |
DBCF is a parallelogram |
Opposite sides CF and BD are
equal and parallel |
|
|
9 |
DF||BC,DF=BC |
From Step 8 |
|
|
10 |
DE=EF |
From Step 5 |
|
|
11 |
BC = 2DE |
From Step 9 and Step 10 |
|
6.8.7 Converse of midpoint theorem: The straight line
drawn through the mid point on one side of a triangle and parallel to another
bisects the third side.
Data: In triangle ABC, D is mid
point of AB. DE||BC
To prove: E is mid point of AC
Construction: From C draw a line parallel
to AB. Extend DE to meet this line at F
Proof:
|
Steps |
Statement |
Reason |
|
|
1 |
BD = CF |
DBCF is parallelogram |
|
|
2 |
AD = BD |
Given D is mid point of AB |
|
|
|
Consider |
||
|
3 |
AD=CF |
|
|
|
4 |
|
Alternate angles of AB||CF |
|
|
5 |
|
Vertically opposite angles |
|
|
6 |
|
ASA Postulate |
|
|
7 |
AE=EC |
Step 6 |
|
6.8.7 Problem 8: Prove that the figure
obtained by joining the mid points of adjacent sides of a quadrilateral is a
parallelogram.
Given: P, Q, R, S are the mid
points of AB, BC, CD, DA respectively, of quadrilateral ABCD.
To Show: PQRS is a parallelogram
Construction: Join BD.
|
Steps |
Statement
|
Reason |
|
|
1 |
PS||BD and 2PS=BD |
Midpoint theorem for |
|
|
2 |
BD||RQ and 2RQ=BD |
Midpoint theorem for |
|
|
3 |
i.e. PS||RQ
and 2PS=2RQ or PS=RQ |
From Step 2 |
|
|
4 |
PSRQ is a
parallelogram |
From Step 3 |
6.8.7 Problem 9: Prove that the figure
obtained by joining mid points of the adjacent sides of a rhombus is a
rectangle
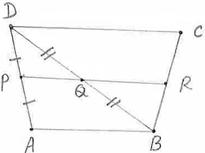
Given: P, Q, R, S are the mid
points of AB, BC, CD, DA respectively of quadrilateral ABCD
To Show: PQRS is a rectangle.
Construction: Join BD and AC
Proof:
Firstly, follow the steps
described above to show that PQRS is a parallelogram.
|
Steps |
Statement
|
Reason |
|
|
1 |
AO=OC,OD=BO and AOD= 900 |
In a rhombus diagonals bisect
each other perpendicularly |
|
|
2 |
|
Sum of angles in a triangle |
|
|
3 |
|
Step 1, Step 2 |
|
|
4 |
|
SR||AC and |
|
|
5 |
PS||BD |
(Mid point theorem) |
|
|
6 |
|
Corresponding angles(Step 5) |
|
|
7 |
|
Step3,Step 4 and Step 6 |
|
|
8 |
= 1800 -900 =900 |
ASD is a straight line and step
7 |
|
|
9 |
|
Similar steps 2 to Step 8 |

6.8.7 Problem 10: In the following figure
with AB||CD, prove that R is the mid point of BC and PR = 1/2(AB+DC)
Given: P and Q are midpoints of AD
and BD respectively, AB||CD
To Show: R is mid point of BC, PR
= 1/2(AB+DC)
|
Steps |
Statement |
Reason |
|
|
1 |
PQ||AB and PQ=1/2AB |
Midpoint
theorem for |
|
|
2 |
R is mid point of BC |
Converse
of midpoint theorem for |
|
|
3 |
QR=1/2CD |
Midpoint
theorem for |
|
|
4 |
|
From Step 1 and Step 3 |
|
|
5 |
i.e. PR = 1/2(AB+DC) |
|
Note: From this we
conclude that the length of the line segment joining mid points of two non
parallel sides of a trapezium is half the sum
of lengths of the
parallel sides.
6.8.7 Problem 11: D, E and F are
midpoints of AB, AC and BC of an isosceles triangle ABC in which AB=BC. Prove
that ![]() DEF is also isosceles.
DEF is also isosceles.
Given: D, E and F are midpoints of
AB, AC and BC respectively, AB=BC
To Show: ![]() DEF is an isosceles triangle (any two sides in
DEF is an isosceles triangle (any two sides in ![]() DEF are equal).
DEF are equal).
Solution:
|
Steps |
Statement
|
Reason |
|
|
1 |
2DE = BC |
Midpoint theorem for |
|
|
2 |
2FE = AB |
Midpoint theorem for |
|
|
3 |
AB=BC |
Given |
|
|
4 |
|
Substituting results of step 1 and step 2
in step 3 |
6.8 Summary of learning
|
No |
Points
to remember |
|
1 |
The diagonals of a parallelogram
bisect each other |
|
2 |
Each diagonal divides the
parallelogram in to two congruent triangles |
|
3 |
Parallelograms standing on the same
base and between the same parallel lines have equal areas |
|
4 |
The line joining the mid points of
any two sides of a triangle is parallel to and half the third side |
Some useful formulae for calculation of areas:
|
Type |
Figure |
Area |
|
Triangle |
|
1/2 *ah 1/2* base*height OR
Where s = (1/2) (a+b+c) =1/2(sum of sides) |
|
Quadrilateral |
|
(1/2) *d(h1+h2) 1/2 * diagonal * sum of altitudes on the diagonal |
|
Parallelogram |
|
a*h (base*height) |
|
Trapezium |
|
(1/2) *h(a+b) (1/2) *product of height and sum of parallel sides |
|
Rectangle |
|
ab Product of sides |
|
Square |
|
a*a = a2 Square of sides |
|
Rhombus |
|
(1/2)*ab (1/2)* product of diagonals |
Additional Points:
6.8.7 Intercept Theorem: If three or more lines
make equal intercepts on one transversal, then they make equal intercepts on
any other transversal.
Given: Transversal p makes equal intercepts
(AB=BC) on three lines l, m and n.
(i.e. l || m || n) q is another
transversal which makes intercepts DE and EF.
To prove: DE=EF.
Construction:
|
Steps |
Statement |
Reason |
|
|
|
Consider |
||
|
1 |
|
Corresponding angles (It is given that line l || line m) |
|
|
2 |
AB=BC |
Given |
|
|
3 |
|
ASA postulate on congruence. |
|
|
4 |
AS=BT |
Corresponding sides are equal |
|
|
|
|||
|
5 |
ASED is a parallelogram |
AS||DE(construction), AD||BE(Given) |
|
|
6 |
AS=DE |
Sides of a parallelogram |
|
|
7 |
BTFE is a parallelogram |
BT||EF(construction), BE||CF(Given) |
|
|
8 |
BT=EF |
Sides of a parallelogram |
|
|
9 |
DE=EF |
Steps 4,6 and 8 |
|
6.8.7 Problem 12: D, E and F are the mid
points of the sides AB, BC and CA of the triangle ABC. AE meets DF at O. P and
Q are mid points of
|
Steps |
Statement
|
Reason |
|
|
|
Consider |
||
|
1 |
DF||BC and 2DF = BC |
Mid point theorem (D and F are
mid points) |
|
|
|
Consider |
||
|
2 |
PQ||BC and 2PQ = BC |
Mid point theorem (P and Q are
mid points) |
|
|
|
Consider |
||
|
3 |
DP||AO and 2DP = AO |
Mid point theorem (D and P are
mid points) |
|
|
|
Consider |
||
|
4 |
FQ||AO and 2FQ = AO |
Mid point theorem (F and Q are
mid points) |
|
|
5 |
DF = PQ, DF||PQ |
Steps 1,2 |
|
|
6 |
DP = FQ, DP||FQ |
Steps 3,4 |
|
6.8.7 Problem 13: In a trapezium ABCD,
AB||DC, P and Q are mid points of AD and BC respectively. BP produced meets CD
produced at point E.
Prove that P bisects BE and PQ||AB.
|
Steps |
Statement
|
Reason |
|
|
|
Consider |
||
|
1 |
|
Vertically opposite angles |
|
|
2 |
PD = PA |
Given (P is mid point of AB) |
|
|
3 |
|
Alternate angle AB||DE |
|
|
4 |
|
ASA Postulate |
|
|
5 |
PE=PB |
Step 4 |
|
|
|
Consider |
||
|
6 |
P and Q are mid points of sides
EB and BC respectively |
Step 5 and given |
|
|
7 |
PQ||DC |
Mid point theorem |
|
|
8 |
DC||AB |
Given |
|
|
9 |
PQ||AB |
Step 7 and 8 |
|
6.8.7 Theorem 4:
In a parallelogram prove that opposite sides and opposite angles are
equal
Data: In ABCD AB||CD and AD||BC
To Prove: AD=BC, AB=CD and ![]() ADC =
ADC = ![]() ABC and
ABC and ![]() DAB =
DAB = ![]() DCB
DCB
Construction: Join BD
|
Steps |
Statement |
Reason |
|
|
|
Consider |
||
|
1 |
|
Alternate
angle AB||CD |
|
|
2 |
BD is common |
Construction |
|
|
3 |
|
Alternate angle AD||BC |
|
|
4 |
|
ASA Postulate |
|
|
5 |
AD=BC, AB=CD |
Step 4 |
|
|
6 |
|
Step 4 |
|
|
7 |
|
Addition
of Step 1 and 3 |
|
|
8 |
|
Simplification
of step 7 |
|
Exercise: Prove the following:
|
No |
Theorems: |
|
1 |
A quadrilateral is a
parallelogram if their diagonals bisect each other |
|
2 |
A quadrilateral is a
parallelogram if their opposite sides are equal |
|
3 |
A quadrilateral is a
parallelogram if their opposite angles are equal |
|
4 |
A quadrilateral is a
parallelogram if a pair of opposite sides is equal and parallel |
|
5 |
A parallelogram is a rectangle
if their diagonals are equal |
|
6 |
A parallelogram is a square if
their diagonals are equal and intersect at right angles |
|
7 |
A diagonal of a square makes an
angle of 45o with the sides of the square |
|
8 |
A parallelogram is a rhombus if adjacent
sides are equal |
|
9 |
A diagonal of a rhombus bisects
vertex angles |
|
10 |
The diagonals of a rhombus
intersect each other at right angles |
|
11 |
A parallelogram is a rhombus if
their diagonals intersect at right angles |
|
12 |
A rhombus is a square if their
diagonals are equal |
Hint: Use the following properties/statements to prove all of
the above theorems after drawing diagonals if required.
1. SSS/ASA/SAS
postulates for congruency of triangles.
2. Alternate/Corresponding
angles are equal when lines are parallel.
3. In an isosceles
triangle angles opposite to equal sides are equal.
6.8.7 Problem 14: ABCD is a parallelogram.
A line through A cuts DC at point P and BC produced to Q. Prove that area of ![]() BCP = area of
BCP = area of ![]() DPQ
DPQ
Construction: Draw AE![]() BC and CF
BC and CF![]() AB
AB
|
Steps |
Statement
|
Reason |
|
|
1 |
Area of ABCD = AB*CF=AD*AE=BC*AE |
Formula for area and AD=BC |
|
|
2 |
Area of |
Formula for the area of |
|
|
3 |
Area of |
Formula for the area of |
|
|
4 |
Area of |
AD*AE=AB*CF(step 1),Step2,3 |
|
|
5 |
Area of |
From figure |
|
|
6 |
Area of Area of ABCD - Area of AB*CF – (1/2)*AB*CF = (1/2)AB*CF |
From figure Step 1,3 |
|
|
7 |
= Area
of |
Step 3 |
|
|
8 |
Area of Area of |
Step 4 and 5 |
|
|
9 |
Area of |
Simplification of step 8 |








