3. 8
Relations and Functions:
An ordered pair is a pair of objects, whose orders
are important. By convention they are represented using curve brackets () where
as sets are represented using flower brackets {}.
Let A = {
{
However in case of ordered pair
(
(
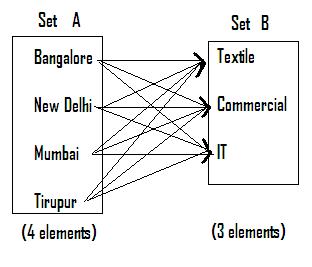Let us assume that you
have been given the following question in an examination for matching.
From examination point of view there can only be
three right matches. However, as it can be seen from the figure (Every element
in set A is paired with every element in set B), There can be 12 possible pairs. Thus we have in all 4*3 =
12 possible pairs.
Observe that ( (IT,
If A and B are two given sets, the set containing
all the ordered pairs where the first element is taken from A and the second
element is taken from B is called ‘Cartesian product’
of two sets. The resulting set is denoted by A
B (read as A cross B).
AB = { (x,y) : x 
A and y B}
In the above figure it can be observed that ( (IT,
Since (x,y)(y,x) AB BA
if A, B and C are three sets then the following can be proved: that
1. A(B
C) = (AB)( AC)
2. A(B
C) = (AB)( AC)
3. (B-C)A = (BA) - (CA)
4. n(AB) = n(A)*n(B) ( n represents number of elements in the set
Some times when we have an ordered pair, it is possible
to have a relationship between the elements of two sets. Some of these
relations are =(is equal to), <(is less than), >(is greater than) , ||(is
parallel to).
A ‘relation’
is a set of ordered pair which explains how elements of one set are related to
elements of other set and the relation is normally denoted by R. Let
A = {Uttar Pradesh, Andhra Pradesh,
B = {
We can have a relationship
called ‘state’s capital is’.
Then, the correct relationships are {(Orissa,
Note that (Bihar, (
The set of first components of all the ordered
pairs of a relation is called its domain
and the set of all their second components is called range of the relation.
Let R = {(a,p), (c,q), (b,r),(b,z)} be a relation then
Domain = {a,b,c}:
which is the set of all the first components of the relation R
Range = {p,q,r,z}: which is the set of all the second
components of the relation R
2.14 Problem 1 : Given that the ordered pairs (a,7)
and (-4,b) belong to the relation {(x,y): 2y-3x=8}.
Find the values of a and b.
Solution:
Since (a,7) satisfies the relation,
2*7
- 3*a = 8
14 - 3a = 8
a = 2
Since (-4,b) satisfies the relation,
2b
- 3*(-4) = 8
2b + 12 = 8
b = -2
In this example,
Domain ={2,-4}
Range
={7,-2}
Types of relations:
‘Reflexive’ (Identity) relation: A
relation R on a set is reflective, if each element of set A is related to
itself. (If a 
A then for R to be reflective (a,a) should R): The relation ‘Greater than’ is not
a Reflective relation.
‘Symmetric’ relation: A relation R
on a set A is Symmetric, if for each ordered pair,(a,b)R,(b,a) alsoR (If a is related to b then for R to be Symmetric, (b,a)
should R). The relation ‘Son
of’ is not a Symmetric relation.
‘Transitive’ relation: A relation R
on a set A is Transitive, if for ordered
pairs,(a,b)R,(b,c)R, then (a,c) alsoR (If a is related to b and b related c then for R to be Transitive, (a,c) should R). The relation ‘Mother
of’ is not a Transitive relation.
‘Equivalance’ relation: A relation R
on a set A is said to be an equivalence relation if the relation is Reflective,
Symmetric and Transitive. The relation ‘is congruent to’ is an equivalence
relation.
A relation from set A to B is called a ‘function’ if for
each element in set A there is one and only one (unique) image in set B and it is
denoted by
f : A
B.
If (x,y) is in f (which is a relation) then we
write y = f(x), where f(x) is called the value of the function at x.
Types of functions:
|
Figure |
Function Name f : A |
Property |
|
|
This is NOT a Function
Since
X1 has two images (Y1,Y2). In a function,
for one value of x there can not be
more than one value of y |
Reason: One
element in set A is mapped onto more than one element in set B and thus it is
not a function. |
|
|
One-one Function For
every value of x there is only one value of y f(X1)
= Y1 f(X2)
= Y2 f(X3)
= Y3 For
example Y
= f(x) = 2x |
Each
element of set B is the image of only one element in set A. ================ The
figure also represents One-one Onto function. (explained
later) |
|
|
Many – One Function Y
has same value for two or more different values of X f(X1)
= Y1 f(X2)
= Y1 f(X3)
= Y1 Y
= X2 is an example |
Two
or more elements in A have the same image in B. |
|
|
Onto Function f(X1)
= Y1 f(X2)
= Y2 f(X3)
= Y2 ================ The
figure also represents Many – one onto function. |
If
each element of set B is an image of at least one element of set A. Thus
there cannot be an element in set B which is not an image of an element in
set A. ================ |
|
|
Into Function f(X1)
= Y1 f(X2)
= Y2 f(X3)
= Y3 ================ The
figure also represents One – one Into function. |
If
there exists at least one element in set B ,which is not an image of any
element in set A. |
|
|
Into Function f(X1)
= Y1 f(X2)
= Y1 f(X3)
= Y3 ================ The
figure also represents Many – one Into function. |
Because of the way function has been defined , we
observe that f is sub set of AB and f(A) is a sub
set of B.
In fact f = {(x,f(x): x A }
2.14 Problem 2 : Let A =
{1,2,3,4,5,6}, B = {-4,-3,-2,0,1,2,3,4} and R = {(x,y): y =2x-5: x A and Y B }
Find the set R, list range and domain of R and name
the type of the function R belongs to
Solution:
Since y = 2x-5 we find that when x = 1, y= -3(=2*1-5) then (1,-3) R
Similarly ( 2,-1),( 3,1), (4,3), (5,5), (6,7) are the other pairs which satisfy the
condition y = 2x-5
We also note of these that, the element 7 in the
last pair(6,7) 
B
Hence because of the definition of R (6,7) R
Domain of R = {1,2,3,4,5}
Since the element 6 in set A does not have an image
in B, R is not a function.
2.14 Problem 3 : If f(x) = x2+2x+3 find [f(x+h) –f(x)]/h
when h 3
Solution:
f(x+h) = (x+h)2+2(x+h)+3
= x2+2hx + h2+2x +2h +3
f(x+h)
–f(x) = x2+2hx + h2+2x
+2h +3 – (x2+2x+3)
= h2+2hx+2h = h(2x+h+2)
[f(x+h) –f(x)]/h =
2x+h+2
If f is a function such that f : A
B, and f= {(x,y), xA,y B }
Then ‘inverse of f’
is defined as f-1 = {(y,x) ; (x,y) f}
Let is
observe the following two figures
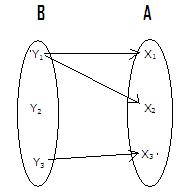
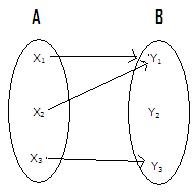
FIGURE
1
FIGURE 2
First figure(f : A B) is a function ( In fact it is ‘Many to one into’ ) and
second figure which is inverse of first
figure f-1 : B A is not a function.
( The reason is that y2 in B does not have a image in
A)
We observe that if and only if, a function is one- one and onto,
then only its inverse is a function.
As an example, note that the inverse of function
f(x) = x2 is not a function. However the inverse of function f(x) =
x3 is f-1(x) = 
Composite functions:
|
If
f : A g : B then
gOf : A (gOf)(x) = g(f(x)) |
|
2.14 Problem 4 : If
f(x) = x+2, g(x) = x and h(x) = x2
Find gOf, hO(gOf), hOg, and (hOg)(Of)
Solution:
{gOf}(x) = g[f(x)]= g(x+2) =x+2
{hO (gOf)}(x) = h[gOf(x)] = h[g{f(x)}] = h[g{x+2}]= h[x+2] = (x+2)2
{(hOg)}(x) = h[g(x)] = h(x) =
x2
{hOg(Of}(x) = (hOg)(f(x)) = (hOg)(x+2)
= h[g(x+2)] =h[x+2] = (x+2)2
In general we can prove that hO(gOf)
= (hOg)Of
2.14 Exercise: if f(x) = 2x+1 and g(x) = x-1/2 show that fOg gOf
3.8 Summary of learning
|
No |
Points
studied |
|
1 |
Relations,
Functions |
