Introduction to Numbers

1.1 Introduction to Numbers:

1.1.1Natural Numbers

Let us look at some objects and the numbers associated with them, We have 1 head, 2 eyes. There are 4 vedas (Rugveda, Yajurveda, samaveda and Atharvaveda)

Hand has 5 fingers. Indian music has 7 Svaras ( Sa Ri Ga Ma Pa Da Ni Sa), 10 fingers . . .

These type of numbers which we come across in our daily life are called natural Numbers. Few more examples are 3, 6, 8,9 …100…1000 and so on

The set (group) of natural numbers is conventionally denoted by N.

N = {1, 2, 3…..}

Note : 0 is not a natural number(why? : Can we associate/identify an object with 0?

Properties of Natural Numbers

Observe the result of addition and multiplication of 2 natural numbers: 3+2 = 5, 3*4 =12

We notice that addition and multiplication of two natural numbers is again a natural number. Then, we say that set of natural numbers satisfies ‘closure property’ with respect to addition and multiplication.

Note that 3-2 = 1 which is a natural number, but 3-4 = -1 is not a natural number.

Since the subtraction of two natural numbers does not always result in a natural number, subtraction does not satisfy closure property.

Also note that 4/2 =2 which is natural number but 2/4 = 1/2 is not a natural number

Since the division of two natural numbers does not always result in a natural number, division does not satisfy closure property.

Have you observed the following?

2+3 = 3+2 , 4+5 = 5+4

Thus for any two numbers a and b a+b = b+a

This property is true for all natural numbers and this property is called ‘commutative property’ with respect to addition

Notice 3-2 2-3 and 5-4 4-5

Thus subtraction does not satisfy commutative property.

2*3 =3*2, 6*5 =5*6

Thus for any two numbers a and b a*b = b*a

This property is true for all natural numbers and this property is called ‘commutative property’ with respect to multiplication.

4÷2 2÷4 , 3÷2 2÷3

Thus division does not satisfy commutative property.

(2+3)+6 = 2+(3+6) , (4+5)+8 =4+(5+8)

Thus for any three numbers a, b and c (a+b)+c = a+(b+c)

This property is true for all natural numbers and this property is called ‘associative property’ with respect to addition

(4-3)-2 = -3

4-(3-2) = 1

(4-3)-2 4-(3-2)

Thus subtraction does not satisfy associative property

(2*3)*6 = 2*(3*6) , (4*5)*8 =4*(5*8)

Thus for any three numbers a, b and c (a*b)*c = a*(b*c)

This property is true for all natural numbers and this property is called ‘associative property’ with respect to multiplication.

(8÷2) ÷2 = 4÷2 =2

8÷ (2÷2) = 8÷1 =8

Since both results are different,

division does not satisfy associative property

Hence for any 3 numbers a, b and c: (a÷b) ÷c a÷ (b÷c)

1.1.2 Whole Numbers:

We have observed that 0 is not a natural number, but what is special about this number?

1+0 = 1, 2-0 =2, 2*0 =0 and 3÷0 is undefined.

You must have heard that Zero is India’s greatest contribution to Mathematics. They were also the first to introduce decimal numbering system.

The 0 and group of natural numbers together is called set(group) of whole numbers and is denoted by

W = {0, 1, 2, 3, 4…..}

Whatever the properties natural numbers have, same properties hold good for whole numbers also.

Properties that do not hold good for natural numbers will not hold good for whole numbers also.

Note :

0 is the ‘identity element’ of addition because; addition of 0 to any number does not change the value of the number

1 is the ‘identity element’ of multiplication because; multiplication of any number by 1 does not change the value of the number

1.1.3 Integers:

We read in news papers that a city has recorded a temperature of -5⁰C. This means that the temperature is 5⁰ C below 0⁰.

How do we understand such numbers which we encounter in our daily life, better?

The integers {1, 2, 3, 4 ….} are called set of positive integers.

The integers {-4,-3, -2, -1 ….} are called set of negative integers.

By convention 0 is neither a positive number nor a negative number.

The group Z = {…..-4, -3, -2, -1, 0, 1, 2, 3, 4….} is called set of integers.

Note that this set consists of positive integers, negative integers and zero.

The integers can be represented on a number line as shown below.

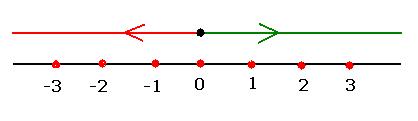
Note that all positive integers are represented to the right of 0 and all negative integers are represented to the left of 0.

If numbers are represented on the number line as given below

What is the distance between 2 and 0 and distance between -2 and 0?

In both the cases the distance is same and it is 2 units.

Definition: ‘Absolute value’ of any number is the same number with + sign. The absolute value of positive number is the number itself. Absolute value of negative number is the same number with positive sign. If x is a number its absolute value is denoted by |x|

Ex. Absolute value of +5 is +5 or 5 and absolute value of -5 is +5 or 5

Absolute value of positive number = Absolute value of negative number

We can symbolically say:

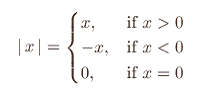
1.1.3.1 Addition of integers:

1) Addition of two positive integers:

(+1) + (+4 )

We observe from the diagram that (+1) + (+4) = +5

To add two positive integers, we add the two and give the sum a positive sign.

2) Addition of two negative integers:

(-1) + (-4)

We observe from the diagram that (-1) + (-4) = -5 =

To add two negative integers, we add their absolute values and give the sum a negative sign.

- {|-1| + |+4|} = - (1+4) = -5

3) Addition of positive and negative integers:

3.1) (+5) + (-3 )

We observe from the diagram that (+5) + (-3) = +2

To add one positive integer and another negative integer find the difference between their absolute values and give the sign of the integer having greater absolute value, to the difference.

3.2) (-4) + (+2 )

We observe from the diagram that (-4) + (+2) = -2

To add one positive integer and another negative integer find the difference between their absolute values and give the sign of the integer having greater absolute value, to the difference.

Explanation:

3.1) Let us take the case of (+5) + (-3 ). Their absolute values are 5 and 3. The difference between these two is 2(=5-3). The integer having greater absolute value is +5 whose sign is +

Therefore the result will have positive sign.

(+5) + (-3 ) = Sign of +5[ Absolute value of (+5) – Absolute value of (-3)] = +[ 5 – 3]= +2 : +[|+5| - |-3|] = + [ 5-3] = 2

3.2) Let us take the case of (-4) + (+2 ). Their absolute values are 4 and 2. The difference between these two is 2(=4-2). The integer having greater absolute value is -4 whose sign is -

Therefore the result will have negative sign

(-4) + (+2 ) = Sign of -4[Absolute value of (-4) – Absolute value of (+2)] = - [ 4 – 2] = - 2 : -[|-4| - |+2|] = - [4-2] = -2

Observations:

1. The sum of two positive integers is positive.

2. The sum of two negative integers is negative.

3. The sum of a positive integer and a negative integer is positive if the +ve integer is greater than the absolute value of the –ve integer.

4. The sum of a positive integer and a negative integer is negative if the absolute value of

the -ve integer is greater than the +ve integer.

1.1.3.2 Subtraction of integers:

Note the following:

Statement	Conversion	Simplification	Result
Subtract 3 from -5	-5 -3	-5 + (-3)	- 8
Subtract 3 from 5	5 -3	5 + (-3)	2
Subtract -3 from -5	-5 –(-3)	-5 + (+3)	-2
Subtract -3 from 5	5 – (-3)	5 + (+3)	8

Subtraction of integers is done in two steps as follows:

1. Change the sign of subtrahend

2. Add by following the rules of addition of integers.

1.1.3.3 Multiplication of integers:

We know that multiplication is a repetitive process of addition. Let us see the result of product of numbers when multiplier/multiplicand is negative.

1.1.3.3.1 When negative number is multiplied by positive number:

When	Multiplier	Multiplicand	Product	Result
Multiplier is Reduced by 1	3	2	6	Product reduces by 2
	2	2	4
	1	2	2
	0	2	0
	-1	2	-2
	-2	2	-4
	-3	2	-6

Product is negative.

1.1.3.3.2 When positive number is multiplied by negative number:

When	Multiplier	Multiplicand	Product	Result
Multiplicand is Reduced by 1	2	3	6	Product reduces by 2
	2	2	4
	2	1	2
	2	0	0
	2	-1	-2
	2	-2	-4
	2	-3	-6

Product is negative.

1.1.3.3.3 When negative number is multiplied by negative number:

When	Multiplier	Multiplicand	Product	Result
Multiplier is Reduced by 1	3	-2	-6	Product increases by 2.
	2	-2	-4
	1	-2	-2
	0	-2	0
	-1	-2	+2
	-2	-2	+4
	-3	-2	+6

Product is positive.

We know Quotient = Dividend/Divisor

Quotient*Divisor = Dividend

The rules of multiplication applicable to negative numbers, apply for divisions when Dividend or Divisor is negative.

1.1.3.4 Multiplication/Division of integers:

Operand	Operation	Operand	Result
+	Multiplication Or Division	+	+
+		-	-
-		+	-
-		-	+

The above table can be expanded to be read as:

1	If a positive integer	is multiplied by	another positive integer	then the product is positive
2	If a positive integer		another negative integer	then the product is negative
3	If a negative integer		another positive integer	then the product is negative
4	If a negative integer		another negative integer	then the product is positive

1	If a positive integer	is divided by	another positive integer	then the quotient is positive
2	If a positive integer		another negative integer	then the quotient is negative
3	If a negative integer		another positive integer	then the quotient is negative
4	If a negative integer		another negative integer	then the quotient is positive

Example : Simplify {(-10)*(-8)*(-4)} ÷{(-5)*(+2)}

(-10)*(-8) = +80 ( product of 2 –negative integers is positive)

(-10)*(-8)*(+4) = (+80)*(-4) = - 320( product of positive and negative integers is negative)

(-5)*(+2) = -10( product of negative and positive integers is negative)

{(-10)*(-8)*(-4)} ÷{(-5)*(+2)}

= (-320) ÷ (-10) = +32 ( quotient of 2 –negative integers is positive)

1.1.3.5 Properties of Integers:

We notice:

-4+ -3 = -7 : 4+(-4)= 0: -4*-3 = 12 : (-4)*(+3) = -12

Also 3-4 = -1 is an integer: 3-3 =0 is an integer

We notice that addition, subtraction and multiplication of two integers is again an integer. Thus, set of integers satisfy closure property with respect to addition, subtraction and multiplication

4÷2 =2 but 2÷4 is not an integer

Since result of division of two integers is not always an integer division does not satisfy closure property.

We also notice the following:

For any two integers a and b a+b = b+a

For any two integers a and b a*b = b*a

For any three integers a, b and c, (a+b)+c = a+(b+c)

For any three integers a, b and c, (a*b)*c = a*(b*c)

Thus, set of integers satisfy commutative and associative properties with respect to addition and multiplication.

Like in the case of whole numbers, 0 is the identity element for addition and 1 is the identity element for multiplication.

Can we find a corresponding integer for every integer such that their sum is zero?

(3,-3), (-4, 4) are such pairs of integers such that their sum is zero. An integer is called the ‘additive inverse’ if the sum of that integer and its additive inverse is zero.

(Integer + Its additive inverse = 0)

-3 is the additive inverse of 3, 3 is additive inverse of -3.

1.1.4 Rational Numbers:

We have come across fractions such as -1/2, 1/4 ,1/2,3/4…….

They are all got by dividing an integer by another non zero integer.

Definition: Rational numbers are set of numbers represented by the form in the simplest form, where p and q are integers with q0. The set is denoted by Q.

Q = { -1, -3/4 -2/3 -1/2, , 0, 1/4 ,1/2, 3/4,2,4…..} or symbolically

Q = { : p, q Z and q0}

Like integers rational numbers can also be represented on a number line as shown below:

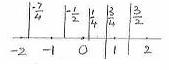
Operations on Rational numbers:

Before any operation, convert mixed number into improper fraction if the number given is a mixed number.

General procedure for Addition/Subtraction:

In order to add/subtract two rationals we need to have same denominators for both the rationals

Step1 : Find LCM of denominators

Step2 : Convert the given rationals to rationals of same denominator

Step3 : Add/Subtract numerators and then divide the result by the common denominator.

Step4 : Simplify if necessary.

1.1.4 Problem 1: Add 7/5 and -2/3

Solution:

LCM of 5 and 3 is 15.

7/5 = 7/5*3/3 = 21/15

-2/3 = -2/3*5/5 = -10/15

7/5 + (-2/3) = 21/15 -10/15 = (21-10)/15 = 11/15

1.1.4 Problem 2: Subtract -3/2 from -8/5

Solution:

LCM of 2 and 5 is 10

-8/5 = -8/5*2/2 = -16/10(note -8*10 = 5*-16)

-3/2 = -3/2*5/5 = -15/10 (note -3*10 = 2*-15)

-8/5 -(-3/2) = -16/10+15/10 = (-16+15)/10 = 1/10

Note: We observe, if a/b and c/d are two rational numbers then

1. They are equal if and only if ad=bc

2. a/b > c/d implies(means) ad>bc( Ex 1/2 > 3/7)

3. a/b < c/d implies ad<bc(Ex 1/2 < 5/9)

4. Every integer is a rational number (If n is a integer then n =n/1)

5. Between two rational numbers there exists many (infinite) rational numbers.

(If a and b are rational numbers then (a+b)/2, (a+b)/3, (a+b)/4….. (a+b)/n are all rational numbers.)

General procedure for multiplication:

Step 1: Find the product of numerators and denominators

Step 2: Divide the product of numerators by the product of denominators and simplify the result if necessary

1.1.4 Problem 3: Multiply 2/7 by -8/11.

Solution:

Product of numerators = 2*(-8) = -16

Product of denominators = 7*11 = 77

2/7 *-8/11 = -16/77

General procedure for Division:

Step 1 : Find out the multiplicative inverse of divisor.

Step 2 : Multiply dividend by the number arrived in step1

1.1.4 Problem 4: Divide -2(1/2) by 8/15

Solution:

1. Convert mixed dividend to improper fraction -2(1/2) = -5/2

2. The multiplicative inverse of divisor is 15/8

-2(1/2) ÷ (8/15) =(-5/2) *(15/8) = -75/16

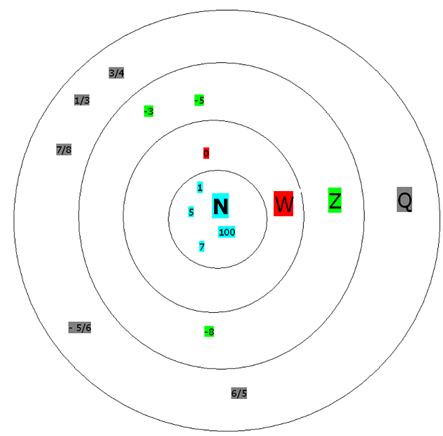Grouping of numbers:

Let us group the different types of numbers studied so far. Let few numbers be

1 3/4 7/8 - 5/6 6/5

5 7 1/3 -8

0 100 -3 -5

1) First we have the group of natural numbers: N = { 1 5 7 100 }

Let us include 0 in to the above group.

2) Then we have the group of whole numbers: W = {0 1 5 7 100 }

Let us include negative integers in to the above group.

3) Then we have the group of Integers: Z = { -8 -5 -3 0 1 5 7 100 }

Let us include rational numbers in to the above group.

4) Then we have the group of rational numbers: Q = { -8 -5 -3 -5/6 0 1/3 3/4 7/8 1 6/5 5 7 100 }

The adjacent figure represents the relationship between set of natural numbers (N), set of whole numbers (W), set of integers (Z) and set of rational numbers (Q)

We notice that N is a sub group of W which itself is a sub group of Z which it self is a sub group of Q

Thus symbolically NW ZQ.

Observations:

1. All the rules that apply for operations on set of natural numbers hold good for set of whole numbers.

2. All the rules that apply for operations on set of whole numbers hold good for set of integers.

3. All the rules that apply for operations on set of integers hold good for set of rational numbers.

The operations which apply are addition/subtraction/multiplication/divisions.

The rules which apply are closure, commutative and associative properties.

Note: Set of rational numbers is not closed under division because (1/2) ÷0 is undefined.

Like in the case of natural numbers, set of rational numbers is not commutative with respect to subtraction and division.

For example 1/2 –1/4 = 1/4 and 1/4 -1/2 = - 1/4

Since 1/4 -1/4 , 1/2 –1/4 1/4 -1/2

For example (1/2) ÷ (1/3) = 3/2 and (1/3) ÷ (1/2) = 2/3

Since 3/2 2/3, (1/2) ÷ (1/3) (1/3) ÷ (1/2)

Similarly associative property does not hold good for subtraction and division of rational numbers.

Like in the case of integers

1. 0 is the identity element for addition of rational numbers.

2. 1 is the identity element for multiplication of rational numbers.

3. Every rational number has an additive inverse (for every p/q, we have -p/q as its additive inverse)

4 Every non zero rational number has a multiplicative inverse (reciprocal.)

For example (-2/3)* (-3/2) =1

Thus, (-3/2) is the multiplicative inverse (reciprocal) of (-2/3)

1.1 Summary of learning

No	Points studied
1	Properties of numbers, whole numbers, integers, rational numbers ( associative, commutative)
2	Representation of numbers on the number line.

Additional Points:

Distance between two numbers on the number line:

If x and y are two numbers on the number line then either x>y or y>x. Let us assume y>x then:

No	Possible values of x and y	Figure	Distance between x and y
1	x> 0 and y>0		y-x
2	x<0 and y <0		PQ = OP-OQ = -x-(-y) =-x+y = y-x
3	x<0 and y>0		PQ = OP+OQ =-x+y =y-x