1.6 Real Numbers:

 

We have studied properties of  Natural numbers, Whole Numbers, Integers, fractions, irrational number such as and . We have also studied that every non zero number has a negative number associated with it such that their sum is zero.

 

The combined set of rational numbers and irrational numbers is called ‘real number’ and is denoted  by R. Note that a number can be either a rational number or an irrational number and it can not be both.

Therefore

If Q is set of rational numbers and Ir is set of irrational numbers then we say Q Ir = (null set)

The relationship between various types of numbers can be represented in a tree structure as follows:

If

N is Set of Natural numbers, W is set of Whole numbers, Z is set of Integers ,Q is set of Rational numbers, R is set of Real numbers and Ir  is set of Irrational numbers

then

 

 

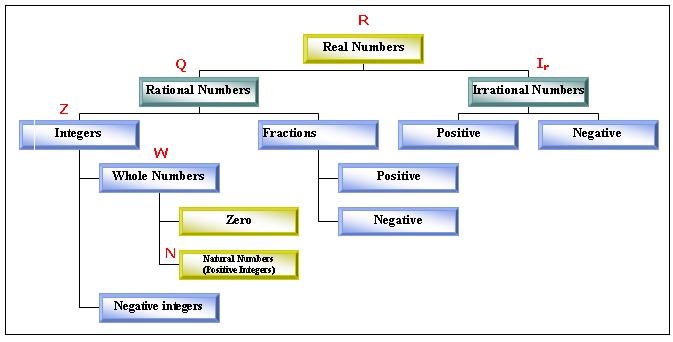
The above relationship can also be expressed using a Diagram (called Venn diagram) as follows:

 

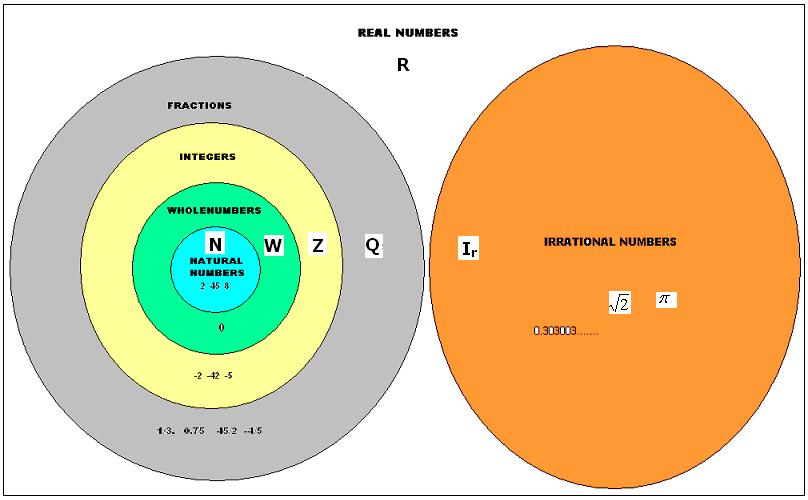
Notice  that

NW  Z  Q R and IrR and QIr = R

 

If a, b, c  R where R is the set of real numbers then

 

No

Relationships

Name of  the property

1

a=a

Reflexive property

2

If a=b then b=a

Symmetric property

3

If a=b and b=c then a=c

Transitive property

4

If a=b then a+c =b+c, ac=bc

 

5

If ac=bc and c  0then a=b

 

6

a+b    R

Closure property of addition

7

a-b    R

Closure property of subtraction

8

a*b   R

Closure property of multiplication

9

a/b   R provided b0

Closure property of division

10

a+b = b+a

Commutative property of addition

11

a*b = b*a

Commutative property of multiplication

12

(a+b)+c = a+(b+c)

Associative property of addition

13

a*(b*c) = (a*b)*c

Associative property of  multiplication

14

a*(b+c) = a*b + a*c, (b+c)*a = b*a+c*a

Distributive law

15

a+0 =0+a =a

0 is additive  identity

16

a*1= 1*a=a

1 is multiplicative  identity

17

a+ (-a) = 0

-a, the additive inverse exists  for every a

18

a*1/a =1 provided a0

1/a,  the multiplicative inverse exists for every a

 

If a, b and c are real numbers then their order relations are:

1

Either a=b or a<b or a>b

 

2

If a <b

Then b>a

3

If a<b  and b <c

Then a<c

4

If a<b  and for any value of c

Then a+c < b+c

5

If a<b

Then ac< bc if c>0

Then ac > bc  if c<0

 

1.6 Problem 1: Solve (x-3)/x2+4 >= 5/x2+4

 

Solution:

 

Solve means finding value of x

Multiplying both sides of the given statement by x2+4 we get

(x-3)>= 5( x2+4 >0)

x >=5+3 (Add 3 to both sides)

x >=8

Verification: By substituting value of x =8,9 notice that the the given statement is satisfied.

 

Euclid's Lemma

Lemma  is a proven statement which is used to prove another statement

We know that

Dividend = (Divisor*Quotient)+Reminder with 0 reminder< Divisor

This relationship is called Euclid's Division Lemma.

It is also stated as follows:

For any positive  integers a and b there exists unique integers q and r such  that

a=b*q+r  with 0 r<b

Alternate way of finding HCF:

We  have learnt in earlier class finding of HCF  by factorisation method and division method.

Using Euclid's division lemma, we can also find HCF.

In this method, starting with  small number as first divisor, we successively divide divisor of each step by reminder of that step till reminder becomes zero, Then the last divisor is HCF.

 

1.6 Problem 2: Find HCF of 305 and 793

 

             Solution:

Divisor

Division

Quotient

Reminder

305

305)793(2

      610

2

183

183

183)305(1

      183

91

122

122

122)183(1

       122

1

61

61

61)122(1

     122

2

0

 

Thus 61 is HCF.

 

1.6 Problem 3:  The length and breadth of a rectangular field is 110m and 30m respectively. Calculate the length of the longest rod which can measure the length and breadth of the field exactly.

 

Solution:

Divisor

Division

Quotient

Reminder

30

30)110(3

      90

3

20

20

20)30(1

     20

1

10

10

10)20(2

     20

2

0

 

Thus HCF is 10

With a rod of length of 10M, we can measure the length and breadth of the field exactly.

          A natural number(>1) which is not prime is called composite number

Note that 24= 2*2*2*3= 3*2*2*2 and 55=11*5= 5*11

Thus, every composite number can be expressed as product of primes in a unique way ignoring the order of the terms. This us called fundamental theorem of arithmetic.

 

1.6 Problem 3:  Find HCF and LCM  of 18,81 and 108

 

Solution:

18=2*9=  2*32

81=9*9=34

108 = 12*9 = 4*3*9 = 22*33

 

HCF = 32=9

LCM = 22*34= 4*81= 324

 

Note  that HCF*LCM of 3 numbers  product of 3 numbers

 

Theorem: If a prime number p divides a2 then p divides a, where  a is natural number > 1

 

Proof : Let a = p1*p2*p3* … *pn  where   p1,p2,p3, … ,pn  are prime factors of a

Squaring both sides gives

a2=( p1*p2*p3* … *pn)2

Since it is given that p divides a2,  p  is a factor of p12*p22*p32* … *pn2

 p has to be one among   p1,p2,p3, … ,pn .

Hence the conclusion is that p divides a

 

1.6 Problem 3:  Prove that  where p is a prime number is irrational

 

 

Solution:

 

Assume  is not rational, then = a/b( simplest form)

pb2= a2=( p1*p2*p3* … *pn)2 where   p1,p2,p3, … ,pn  are prime factors of a.

This means that p  divides  a( p is a factor of a)  and hence a=kp for some value of k

 pb2=k2p2

 b2= k2p

  p is a factor of b

In the earlier step we have concluded that p is a factor a. now we are concluding that p is a factor of b also.

This means p divides both a and b which is a contradiction as we  have said earlier that a/b  is in simplest form.

Note that

Rational number+ Irrational number = Irrational number( Ex. 3+)

Rational number*Irrational number = Irrational number( Ex 4)

 

 

1.6 Summary of learning

 

No

Points studied

1

2

 

3

4

Real numbers and their properties

Relationship between real numbers and other types of numbers.

Sum of rational and irrational number is irrational

Product of rational and irrational number is irrational