1.10
Probability
Introduction:
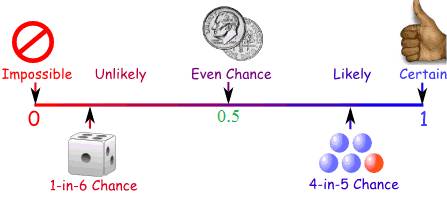
The above picture summarises chances of
some thing happening from 'impossible' to 'possible'.
As we know
‘probability’ means chance of some thing happening. It could be any of the
following:
1. The
chances of rains on any particular day
2. The
chances of
3. A
cricketer scoring century in a particular test match
4.
5. Number
of times head comes up when 1 rupee coin is tossed up 100 times
6. Number
of times number 2 appears when a dice is
drawn 500 times
The outcome of any of the above event is pure chances. It
may happen or it may not happen. Do you notice the difference between first 4 statements and the last 2
statements? In case of first 4 cases, the result depends upon external factors
such as place, time, strength of opposition team.. where as result of 5 and
6 will almost be same irrespective of
place and time of the event. There are
cases when outcome of certain events can be forecast with some certainty. One
such event is tossing of coin. When we toss the coin there can only be 2
outcomes, either head appears or tail appears. When coin is tossed up several
times obviously, the chances of head coming up can vary from 0% to 100% and
tail coming up can vary from 100% to 0%. However when coin is tossed up in large number of times(in
thousands) head coming up may be 50% and
tail coming up could be 50%.
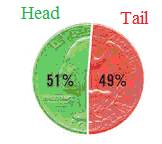
In such cases, the
probability is 1/2. Note that when head appears tail can not appear at the same
time. Similarly when tail appears, head can not appear at the same time.
This we say that events are exclusive.
That is to say, there can not be any other possibility other than head
appearing or tail appearing. In such case, we note that the sum of their
probability is 1/2+1/2= 1. Note that probability is expressed
as a ratio and it is always ≤ 1.
why does dice have dots numbers from 1 to 6?.
Note that dice is a
cube and it has 6 faces. Hence their faces are represented by 1 to 6 dots
representing numbers from 1 to 6. When a dice is cast what are the chances of a
number appearing from 1 to 6? It is one out of 6 and hence the probability is
1/6.
What is the sum of
probabilities of number appearing between 1 and 6?
It is = Probability
of number 1 appearing+ Probability of number 2 appearing + Probability of
number 3 appearing + Probability of number 4 appearing + Probability of number
5 appearing + Probability of number
appearing between 1 and 6
=
1/6+1/6+1/6+1/6+1/6+1/6= 1
(Note that, when
one number appears when a die is cast, other number can not appear at the same
time. Since probability of each number appearing is excusive of others, sum of
their probabilities is equal to 1.
Probability of
number 1 not appearing
= Probability of
number 2 appearing + Probability of number 3 appearing + Probability of number
4 appearing + Probability of number 5 appearing + Probability of number 6
appearing = 1/6+1/6+1/6+1/6+1/6= 5/6
This also can be
calculated as
Probability of
number 1 not appearing = 1 - Probability of number 1 appearing = 1-1/6= 5/6
Let us learn some
of the definitions of terms used
|
No |
Term |
Meaning |
Examples |
|
1 |
Experiment |
Test
or a procedure or operation which produces a result. In this lesson all
experiments will be random. |
|
|
2 |
Trial |
Performing
an experiment |
tossing
a coin/throwing a dice |
|
3 |
outcome |
Result
of trial |
head
or tail/ appearance of number from 1 to 6. |
|
4 |
Sample
space |
Set
of all possible outcomes |
S
= {H,T}. S = {1,2,3,4,5,6} |
|
|
Event |
Every subset of
Sample Space |
Getting
the head=A= {H}, Getting
the number 4=B={4} Getting
even numbers= C = {2,4,6} |
|
5 |
Elementary
event |
Each
of the outcome in sample space. That is
each of the element in sample space. (Every subset of sample space
having only one element) |
Getting
the head=A= {H}, Getting
the number 4=B={4} |
|
6 |
Compound
event |
Obtained
by combining one or more elementary events ( Subsets of sample space having
one or more element) |
Getting
all three heads A= {HHH} Getting
at least 2 tails B = {HTT, TTH, THT, TTT} |
|
7 |
Favourable
event |
An
elementary element that occurs |
|
|
8 |
Certain(sure)
event |
If
any one of the event will occur in the trial (probability
of sure event is 1) |
When
a die is cast the probability of getting a number > 0 and < 7 is 1. (Because when the die is cast the
numbers got are always between 1 and
6). |
|
9 |
Impossible
event |
An
event which will not occur in any of the trial (Probability
of impossible event is 0) |
when
a die is cast the probability of getting number <1 or >6 is 0.(Because
this event will not occur at all). |
|
10 |
Complementary
event |
Converse
of elementary event. if element A is denoted by A
then complementary event is denoted by and
A |
Getting
head A = {H}, converse of this is not getting head that is getting tail.
Hence Getting
the number 4, B={4}, converse of this is not getting 4, that is getting
numbers 1,2,3,5 and 6. Hence |
|
11 |
Mutually
exclusive event |
2
or more events are said to be mutually exclusive if those events do not occur
simultaneously, that is they do not happen together |
Let
S = {1,2,3,4,5,6}, A = {1,2,3}, B = {4,5} Here
A and B are mutually exclusive, because either A occurs or B occurs. they do
not occur at the same time. Also
note that A |
|
Experiment |
Sample
space and Events |
No
of events n(S) |
Event
A |
Favourable
outcomes to event A and n(A) |
Probability P(A) =
n(A)/n(S) |
Complementary
Event( not A= |
Probability
of Complementary Event P( =
n( |
|
1
coin is tossed |
S={ H,T } |
2 |
Tail
coming up |
A=(T) n(A)=1 |
1/2 |
head
comes up= (H) n( |
1//2 |
|
2
coins are tossed |
S={ HH,HT,TH,TT } |
2*2=4 |
Tail
should not come up |
A
= {(HH)} n(A)=1 |
1/4 |
Tail
comes up n( |
3/4 |
|
3
coins are tossed |
S={ HHH,HHT,HTH,THH,
HTT, THT,TTH,TTT } |
2*2*2=8 |
Same
face coming up |
A=
{(HHH),(TTT)} n(A)=
2 |
2/8 |
Not
all same faces n( |
6/8 |
|
1
dice is cast |
S={1,2,3,4,5,6 } |
6 |
Even
number coming up |
A={2,4,6} n(A)=
3 |
3/6 |
Odd
number coming up n( |
3/6 |
|
2
dices are cast |
S={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6) (2,1),(2,2),(2,3),(2,4),(2,5),(2,6) (3,1),(3,2),(3,3),(3,4),(3,5),(3,6) (4,1),(4,2),(4,3),(4,4),(4,5),(4,6) (5,1),(5,2),(5,3),(5,4),(5,5),(5,6) (6,1),(6,2),(6,3),(6,4),(6,5),(6,6) } |
6*6=36 |
Getting the same number |
A=
{(1,1),(2,2),(3,3), (4,4),(5,5),(6,6) n(A)=
6 |
6/36 |
Different
numbers n( |
30/36 |
P(E) =
Probability of an event PE = 
=
Observe that P(A)+
P(
) =1 ( 
n(A)/n(S) + n()/n(S) ={ n(A) + n()}/n(S) = n(S)/ n(S)
)
P(A)
=1- P(), P() =1- P(A)
Probability:
It is the ratio of the number of elementary elements favourable to the event E
to the total number of elements in the sample space
Can probability ratio be 0 or 1?
1. What is the probability of getting a number 0 or greater than 6 when dice is cast?
In this case A = {} an empty
set, and n(S) = 6 , hence P(A)= n(A)/n(S)= 0 (When a dice is cast number is one among 1 to 6 only). This we call an impossible event,
because such a event does not happen
2. What is the probability of getting a number 1 to 6 when dice is cast?
In this case A = S and hence n(A) = n(S) = 6 , Thus P(A)= n(A)/n(S)= 1 (When a dice is cast number is always one among 1 to 6). This we call a sure event, because such a event always happens
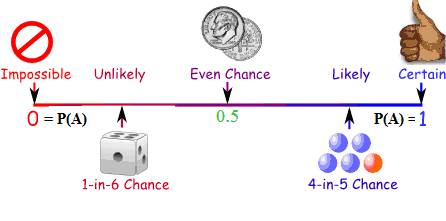
Thus 0 ≤ P(A) ≤
1 This is what we represented in the beginning by a figure:
Problem
1 : A game consists of rolling 2 dices. If the
sum is 2,3,4,5,10,11 or 12, player A wins. If sum is other than these, then
player B wins. Of you want to win, would you be player A or player B?
Solution:
Let A = {
combination of dices whose sum is 2,3,4,5,10,11 or 12 }= {
(1,1),(1,2),(2,1),(1,3),(3,1),(2,2),(1,4),(4,1),(2,3),(3,2),(4,6),(6,4),(5,5),(5,6),(6,5),(6,6)
}
Then B= ={ combination
of dices whose sum is not 2,3,4,5,10,11 or 12 }= { combination of dices whose
sum is 6,7,8, or 9 }
=
{(1,5),(5,1),(2,4),(4,2),(3,3),(1,6)(6,1),(2,5),(5,2),(3,4),(4,3),(2,6),(6,2),(3,5),(5,3),(4,4),(3,6),(6,3),(4,5),(5,4)}
Note that n(A)= 16 and n() = 20. Thus number of elementary elements= 36( Other
wise also note 6*6=36: fundamental principle of computing)
P(A) =
16/36 = 0.4444 and P()= 20/36= 0.55555
Obviously Any one
would like to be B.
Mutually exclusive
event
Let S =
{A1, A2, A3 …. An} Clearly n(S)= n,
P({A1})= 1/n , P({A2})=1/n, P({A3})=1/n … P({An})=
1/n
We note
that, P({A1})+ P({A2})+ P({A3})+ . . . P({An})=
1/n+1/n+1/n + . . . 1/n= n/n= 1
So, sum
of the probabilities of all the elementary events of an experiment is 1.
Let E1
and E2 be two mutually exclusive elements, that is they will not
have any common elements. We have observed that E1
E2 = {
}
They
being disjoint sets, from set theory, we know n(E1
E2) = n(E1)+n(E2)
n(E1E2)/n(S)= n(E1)/ n(S)+n(E2)/
n(S)
P(E1E2) = P(E1)+P(E2)
In general
if E1, E2, E3 . . . En are mutually
exclusive elements then P(E1E2E3 . . . En ) = P(E1)
+P(E2)+ P(E3)+ . . . P(En)
Problem
2 : When a die is thrown, find the probability
that either an odd number or square number occurs
Solution:
S= {1,2,3,4,5,6},
n(S)=6
A= { Odd numbers or
square numbers} = {1,3,4,5}, n(A)=4
P(A)
= 4/6
Problem
3 : The outcome of a random experiment results
in either success or failure. If the probability of success is thrice the
probability of failure, find the probability of success
Solution:
P(A)
=Probability of success, Probability of failure= P()
P(A) = 3P() =3x, we also know that P(A)+P() = 1;
P(A)+
1/3P(A)=1
4P(A)= 3 P(A)= 3/4
Problem
4:
Three squares of a chess board are selected in random. Find the probability of
getting two squares of one colour and the other of different colour.(here
square represents smallest square on which chess is played)
Solution:
Note that chess
board has 64 smallest squares.
3 squares can be
selected in 64C3 ways. Hence n(S)= 64C3 =64*63*62*61!/61!*3!= 64*63*62/2*3= 64*21*31
Number Of black coloured squares = 32, Number of white coloured
squares=32
2 squares can be got in 32C2 ways. 1 square can be got in 32C1 ways.
If A is number of
ways getting two squares of one colour and the other of different colour, then
n(A)= [{32C2}*{32C1}]=[{32*31/2!)}]*{32}=32*31*16
P(A)
= 32C2*32C1/64C3=
32*31*16/64*21*31=8/21
Problem
5 : A committee of 5 persons is selected from
4 men and 3 women. What is the probability that the committee will have
(i) one man (ii) 2 men
(iii) 2 women (iv) at least 2 men
Solution:
Note that total
number of people available to form the
committee is 7.
Hence number of
ways of forming different 5 member committees = 7C5=
7*6/2!= 21= n(S)
(i) one
man in the committee:
Since there are
only 3 women, we will need 2 men to form a committee of 5. Hence, the
probability of forming a committee having
one man is 0
(ii) 2 men in the committee:
Number of ways
committees that can be formed with 2 men from 4 men =4C2= 4*3/2!= 6
Remaining 3 members are to be
women.
Number of ways
committees that can be formed with 3
women from 3 women =3C3= 1
The number of
committees that can be formed with 2 men and 3 women = 6*1=6 ---------(1)
Probability = 6/21= 2/7
(iii) 2 women in the committee:
Number of
committees that can be formed with 2 women from 3 women = 3C2= 3/1!= 3
Remaining 3 members are to be men.
Number of ways
committees that can be formed with 3 men
from 4 men =4C3=4/1!= 4
The number of
committees that can be formed with 2 women and 3 men = 3*4=12 -----------(2)
Probability = 12/21= 4/7
(iv) at least 2 men in the committee:
Number of
committees that can be formed with at least 2 men
= Number of
committees that can be formed with 2 men+ Number of committees that can be
formed with 3 men+ Number of committees that can be formed with 4 men
First we need to
find number of committees that can be
formed with 4 men.
Number of
committees that can be formed with 4 men from 4 men = 4C4= 1
Remaining 1 member has to women.
Number of ways
committees that can be formed with 1
woman from 3 women =3C1=3*2!/2!*1!= 3
The number of committees
that can be formed with 1 woman and 4 men = 1*3=3 ------------------(3)
Number of committees
that can be formed with at least 2 men = 6+12+3
=21
Probability = 21/21= 1
Problem
6 : As shown in the adjoining figure a dice
has been cast in the rectangular shaped area. What is the probability of die
falling inside the circle of diameter 1m inside the rectangular area?
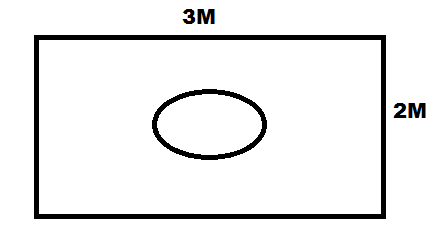
Solution:
Area of rectangular area= ಆಯತದ
ವಿಸ್ತೀರ್ಣ =6 sq.m.
Area of circle = 
*
* sq.m..(
Radius is ಮೀ. )
Probability of dice falling inside circle = Area of circle÷ Area of rectangle
=** ÷ 6=
1.1 Summary of learning
|
No |
Points studied |
|
1 |
Probability,Event,Favourable event, exclusive Event |