1.8 ∏¿AS…ÂU¿º¿ e…∆√q¿u… (Progressions of numbers :)
P…º¿V£¿ D∏¿Q€z¡Ai¿ƒP¿ ´≤µ¿÷
∏¿™¿ƒ∏…ÂU¿º¿£¿ƒþ £…∆√q¿ƒ™¡.
∏¿™¿ƒ∏… 1 :Ý §√™¿≈ §™¿ƒ‰ ∏…þ√ªv¿§Az¿ g¿∆ 10,000 ∏¡Æ •¿q…¢¢ð√g…Az¿ƒ wΩAi¿ƒƒ™¡
™¿ƒv¿ƒ€Ý ∏¿ÈÆý ∏¿ÈÆý™¡VAi…ƒ√ •¿Êw√ ¢£¿
™¡•¡∏¿ƒ P…∆q¿ƒw€√g…Az¿ƒ M¶ý¢ð√j. Ez¿P…à P…Æ™¿≈ DAi…ƒÃU¿Ω™…:
1. §√™¿≈ ¢£¿P…∆ÃAz¿ƒ g¿∆•¡¨ƒAi¿ƒAv…
™¡•¡∏¿ƒ P…∆q¿Æƒ ßAi¿ƒ∏¿ƒw€√j. Ez¿P…à §™¿ƒ‰ ∏…þ√ªv¿ M•¿≈ýv¡€£…Ai¿ƒ ? RArv¡ EÆË.
KP…Az¿g… ∏¿A•¿«t ∏¡Æ w√j∏¿Æƒ ∏¿ƒ™¿i¡g¿ƒ 28 ™¿µ¿U¿º¿ƒ ®…√P¿ƒ.(10,000/365).
2.
§√™¿≈
•¿Êw√¢£¿ ¢£¿z¿ P¿Ê™¿ƒ∏¿AS…ÂAi¿ƒµ¿ƒ÷ g¿∆•¡¨ƒU¿º¿£¿ƒþ P…∆q¿ƒw€√g…Az¿ƒ ®s¡´∏¿ƒ™¡.(1 £…√ ¢£¿ 1 g¿∆. 2£…√ ¢£¿ 2 g¿∆, 3£…√ ¢£¿ 3 g¿∆. . . . . . ª√U…) DU¿ ∏¡Æ w√j∏¿Æƒ Jµ¿ƒ÷ ¢£¿ ®…√P¿ƒ
?
3.
§√™¿≈
™…∆z¿Æ ¢£¿ 1
g¿∆. P…∆lƒ÷ ™¿ƒƒA¢£¿ •¿Êw√¢£¿U¿º¿∞Ë ªA¢£¿ ¢£¿ P…∆l÷ ∫¿tz¿ Jg¿q¿g¿µ¿ƒ÷
P…∆q¿ƒ´g¡z¿g…,( 1 £…√ ¢£¿ 1 g¿∆. 2£…√
¢£¿ 2
g¿∆, 3£…√
¢£¿ 4
g¿∆ 4£…√
¢£¿ 8g¿∆Ý . . . . ª√U…) ∏¡Æ w√j∏¿Æƒ Jµ¿ƒ÷ ¢£¿ ®…√P¿ƒ?
P…∆£…Ai¿ƒ Jg¿q¿∆ ∏¿Az¿®s¿U¿º¿∞Ë ∏¡Æ w√j∏¿Æƒ ®…√P¡z¿
¢£¿U¿º¿ ∏¿AS… P¿Aq¿ƒ ªrAi¿ƒƒ™¿≈z¿ƒ ∫…√U… ?
∏¿™¿ƒ∏… 2 :
§√™¿≈ MAz¿ƒ 70 Q.´ƒ√. z¿∆g¿z¿
∏… P¿ØÔ g…√∏Ô£¿∞Ë ®s¡U¿™¿ª∏¿Æƒ ßAi¿ƒ∏¿ƒw€√g…Az¿ƒ ®s¡´∏¿ƒ™¡. ™…∆z¿Æ U¿Am…Ai¿ƒ∞Ë
16 Q.´ƒ√ z¿∆g¿ Z¿∞∏¿ƒw€√j. ™¿ƒƒA¢£¿ •¿Êw√ U¿Am…Ai¿ƒÆ∆Ë §™¿ƒ‰ ™…√U¿ MAz…∆Az¿ƒ
Q.´ƒ√.£¿Av… P¿r™…ƒAi¿i¡U¿ƒ™¿≈z¡z¿g…. ∏¿ýzs…Ai¿ƒ CAw™¿ƒ ∫¿Av¿™¿£¿ƒþ v¿Æƒ•¿Æƒ
§™¿ƒU… Jµ¿ƒ÷ ∏¿™¿ƒAi¿ƒ ®…√P¿ƒ ?
ÝÝÝÝ
F j√wAi¿ƒ, §v¿Âf√™¿£¿z¿ ∏¿™¿ƒ∏…ÂU¿ΩU… U¿t¬v¿±¡∏¿€Á
∫…√U… ∏¿∫¡Ai¿ƒ ™¿i¡q¿ƒv¿€z…Az¿ƒ wΩAi¿ƒƒ™¡.
18.1 ±…Ê√r¸U¿º¿ƒ
(Sequence) :
1.8.1 Gz¡ 1 : §™¿ƒ‰ ±¡Ø…Ai¿ƒ∞Ë£¿ JØ¡Ë v¿g¿U¿wU¿º¿£¿ƒþ ßg…Ai¿ƒÆƒ
∫…√Ωz¿g… ∫…√U… ßg…Ai¿ƒƒw€√j ?
3, 10, 4, 1, 12, 8, 7, 5,
6, 2, 9, 11 - JAz¿ƒ ßg…Ai¿ƒƒw€√g¡
?
EÆË ßz¿Ø¡V 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,12 - JAz¿ƒ ßg…Ai¿ƒƒw€√j.
1.8.1 Gz¡ 2 : 2006£…√
E∏¿´ d£¿™¿j wAU¿º¿∞Ëg¿ƒ™¿ D¢v¿Â™¡g¿U¿º¿ v¡j√P¿ƒU¿º¿£¿ƒþ ßg…Ai¿ƒ®…√P¡z¿g…, ª√U…
ßg…Ai¿ƒƒw€√j : 1, 8, 15, 22, 29Ý JAz¿ƒ ßg…Ai¿ƒƒw€√j
™…ƒ√∞£¿ Jg¿q¿∆ ∏¿Az¿®s¿U¿º¿∞Ë K£¿ƒ ™¿i¡r¢j ? §™¿ƒU¿j´ÆËz…Ai…ƒ√
§√™…«Az¿ƒ P¿Ê™¿ƒP…à ßz¿Þg¡V, ∏¿AS…ÂU¿º¿£¿ƒþ ßg…¢¢ð√j.
™…∆z¿Æ£…√ ∏¿Az¿®s¿z¿∞Ë 1 jAz¿ Dg¿A©¸π, MAz…∆Az…√ CAP…Ai¿ƒ£¿ƒþ ªA¢£¿ ∏¿AS…ÂU…
P¿∆rπ, ™¿ƒƒA¢£¿ ∏¿AS… ßg…¢j. 12 Dz…∆q¿£… §∞Ëπ¢j. KP…? Cz¿ƒ §™¿ƒ‰ ±¡Ø…Ai¿ƒ∞Ë Eg¿ƒ™¿
P…∆£…Ai¿ƒ v¿g¿U¿w.
Jg¿q¿£…√ ∏¿Az¿®s¿z¿∞Ë 2006£…√ E∏¿´ d£¿™¿j wAU¿º¿ ™…∆z¿Æ g¿´™¡g¿ 1£…√ v¡j√P¿ƒ. Dz¿ðjAz¿ ™…∆z¿Æƒ ë1í£¿ƒþ ßg…z¿ƒ 왿ƒƒAa£¿ ∏¿AS…ÂU… 7£¿ƒþ P¿∆rπî J£¿ƒþ™¿ §Ai¿ƒ™¿ƒP¿Ã£¿ƒ∏¡g¿™¡V ™¿ƒƒA¢£¿
∏¿AS…ÂU¿º¿£¿ƒþ ßg…¢j. P…∆£…Ai¿ƒ ∏¿AS… 31QÃAv¿ P¿r™…ƒ Eg¿ƒ™¿Av… £…∆√rP…∆Arj. KP…Az¿g… d£¿™¿j
wAU¿º¿∞Ë 31¢£¿
™¿i¡v¿Ê´g¿ƒv¿€z….
1.8.1 Gz¡ 3 : F
•¿n÷Ai¿ƒ£¿ƒþ U¿™¿ƒ§π 2, 4, 6, 8, 10, 12 . . . . . .
Ez¿ƒ Ai¿i¡™¿ •¿n÷? Ez¿ƒ ∏¿™¿ƒ∏¿AS…ÂU¿º¿ •¿n÷ ™¿ƒv¿ƒ€ Ez¿ƒ
™¿ƒƒVAi¿ƒƒ™¿≈z…√ EÆË.
™¡ÂS… : MAz¿ƒ ±…Ê√r¸Ai¿ƒƒ
(sequence) §Ai¿ƒ™¿ƒP¿Ã£¿ƒ∏¡g¿™¡V ™¿Â™¿∏…ÐU…∆Ωπg¿ƒ™¿ ∏¿AS…ÂU¿º¿
U¿t™¡Vg¿ƒv¿€z…. ±…Ê√r¸Ai¿ƒ∞Ë£¿ •¿Êw CA±¿™¿≈ ±…Ê√r¸Ai¿ƒ
•¿z¿ (Term) ™¡Vg¿ƒv¿€z….
±…Ê√r¸Ai¿ƒ •¿z¿U¿º¿£¿ƒþ ª√U… ∏¿∆a∏¿ƒv…€√™…, T1 T2T3T4T5
Ö.
|
•¿z¿U¿º¿
P¿Ê™¿ƒ ∏¿AS…ÂÝÝÝÝÝÝÝ ==ý |
1 |
2 |
3 |
4 |
---- |
n |
--- |
|
C£¿ƒP¿Ê™¿ƒ
∏¿∆Z¿P¿ a∫…þU¿º¿ƒÝ
===ý |
T1 |
T2 |
T3 |
T4 |
---- |
Tn |
--- |
MAz¿ƒ ±…Ê√r¸Ai¿ƒ£¿ƒþ ∏¡™¿i¡£¿Â™¡V {Tn Ý} JAz¿ƒ ∏¿∆a∏¿ƒv…€√™….
Jt¬∏¿ß∫¿ƒz¡z¿ Cx¿™¡ §¢µ¿÷ •¿z¿U¿º¿£¿ƒþ ∫…∆A¢g¿ƒ™¿ ±…Ê√r¸Ai¿ƒƒ ë•¿j´ƒv¿ ±…Ê√r¸í(Finite sequence).
Jt¬∏¿Ø¡U¿z¿ Cx¿™¡ C§¢µ¿÷ •¿z¿U¿º¿£¿ƒþ ∫…∆A¢g¿ƒ™¿ ±…Ê√r¸ ëC•¿j´ƒv¿ ±…Ê√r¸í(Infinite sequence).
™…ƒ√∞£¿ ™…∆z¿Æ Gz¡∫¿g¿u…Ai¿ƒ∞Ë
12 •¿z¿U¿Ω™… ™¿ƒv¿ƒ€
2£…√ Gz¡∫¿g¿u…Ai¿ƒ∞Ë 5 •¿z¿U¿Ω™…. E™…g¿q¿∆ •¿j´ƒv¿ ±…Ê√r¸U…
Gz¡∫¿g¿u…U¿º¡V™….
3 £…√ Gz¡∫¿g¿u…Ai¿i¡z¿ ∏¿™¿ƒ ∏¿AS…ÂU¿º¿ •¿n÷Ai¿ƒ∞Ë
§¢µ¿÷ •¿z¿U¿ΩÆË. Dz¿ðjAz¿ Cz¿ƒ MAz¿ƒ C•¿j´ƒv¿ ±…Ê√r¸.
1.8.1 Gz¡ 4 : MAz¿ƒ ±…Ê√r¸Ai¿ƒƒ
©¸£¿þg¡≤U¿ΩAz¿Æ∆ P¿∆rg¿ß∫¿ƒz¿ƒ.
ÝÝÝÝÝÝÝÝÝÝÝÝ 2/1, 3/2, 4/3,
5/4 . . . .Ý
E∞Ë ±…Ê√r¸Ai¿ƒ ∏¡™¿i¡£¿Â•
T1 = (1+1)/1
T2 Ý=(2+1)/2
T3 Ý=(3+1)/3
T4ÝÝÝ =(4+1)/4
Tn=(n+1)/n, F ±…Ê√r¸Ai¿ƒ ∏¡™¿i¡£¿Â •¿z¿¢Az¡V, z¿v¿€ ±…Ê√r¸Ai¿ƒ
Ai¿i¡™¿≈z…√ •¿z¿™¿£¿ƒþ P¿Aq¿ƒªrAi¿ƒß∫¿ƒz¿ƒ.
±…Ê√r¸Ai¿ƒ 6£…√ •¿z¿ T6ÝÝ
=(6+1)/6 =7/6
1.8.1 ∏¿™¿ƒ∏…Â
1 : ÝTnÝÝÝ =2n2+1, Tn=73 Dz¿g… n £¿ ®…Ø… P¿Aq¿ƒªr¨ƒj ?
TnÝÝÝ =2n2+1 =73
2n2 =73-1=72
2n2 =72
n2 =36
n = ![]() =
=![]()
z¿v¿€ ∏¿AS…ÂAi¿ƒ ∏¡È®s¡´P¿ ∏¿AS…ÂAi¿i¡z¿ðjAz¿ n, zs¿£¿ •¿«u¡AP¿™¡Vg¿®…√P¿ƒ ![]() n=6.
n=6.
v¡º…:
T6 = 2*62+1
= 2*36+1=73
1.8.2 ±…Ê√t¬U¿º¿ƒ(Series):
™¡ÂS… : MAz¿ƒ ±…Ê√r¸Ai¿ƒ •¿z¿U¿º¿ ™…∆v¿€™¿£¿ƒþ
±…Ê√t¬ (series) J£¿ƒþv…€√™….
Ez¿£¿ƒþ SÝ Cx¿™¡ Sn §Az¿ ∏¿∆a∏¿ƒv…€√™…. ±…Ê√t¬Ai¿ƒƒ MAz¿ƒ
•¿j´ƒv¿ ±…Ê√r¸Ai¿ƒ •¿z¿U¿º¿ ™…∆v¿€™¡Vg¿ƒv¿€z….
Sn = T1 +
T2+T3.........Tn
Sn- Sn-1=(
T1 + T2+T3.........Tn-1+ Tn)
-( T1 + T2+T3.........Tn-1)=
Tn
Sn- Sn-1Ý = Tn
1.8.2 ∏¿™¿ƒ∏…ÂÝ
1 : TnÝÝÝ ={(-1)n}
Dz¿g…, S1 = S3 : S2
= S4 JAz¿ƒ ∏¡¢¸π.
TnÝÝÝ =(-1)n
T1= (-1)1 =
-1, T2 = (-1)2 =1, T3 = (-1)3 = -1,
T4= (-1)4 = 1
S1 = T1 ÝÝ= -1
S3 = T1 +
T2+T3= -1+1-1 = -1 ÝÝÝÝÝÝ
![]() S1 = S3
S1 = S3
S2 = T1 +
T2Ý =-1+1 =0
S4 =T1 +
T2+T3 +T4= -1+1-1+1 =0 ÝÝÝÝÝÝÝÝÝ
![]() S2 = S4
S2 = S4
1.8.3
∏¿™¿i¡Av¿g¿
±…Ê√r¸U¿º¿ƒ(Arithmetic Progression):
™…ƒ√∞£¿ Gz¡∫¿g¿u… 1.8.1.1
g¿∞Ë, Ai¿i¡™¿≈z…√
Jg¿q¿ƒ C£¿ƒP¿Ê™¿ƒ •¿z¿U¿º¿ ™¿Âv¡Â∏¿ 1 DVz….
Gz¡.1.8.1.2
g¿∞Ë,
Jg¿q¿ƒ C£¿ƒP¿Ê™¿ƒ •¿z¿U¿º¿ ™¿Âv¡Â∏¿ 7
DVz….
™¡ÂS…Â: MAz¿ƒ ±…Ê√r¸Ai¿ƒ∞Ë Ai¿i¡™¿≈z…√ Jg¿q¿ƒ C£¿ƒP¿Ê™¿ƒ •¿z¿U¿º¿ £¿q¿ƒ´£¿
™¿Âv¡Â∏¿™¿≈ πÐg¡AP¿™¡Vz¿ðg…, D ±…Ê√r¸Ai¿ƒƒ ì∏¿™¿i¡Av¿g¿
±…Ê√r¸Ai¿i¡Vg¿ƒv¿€z…î(Arithmetic
Progression)(AP). πÐg¡AP¿™¿≈ ∏¡™¿i¡£¿Â ™¿Âv¡Â∏¿™¡Vg¿ƒv¿€z… ™¿ƒv¿ƒ€ Cz¿£¿ƒþ ëdí¨ƒAz¿ ∏¿∆a∏¿Ø¡U¿ƒv¿€z….
∏¿™¿i¡Av¿g¿
±…Ê√r¸Ai¿ƒ∞Ë,Ý Tn+1 ñ
TnÝ =d : Tn-1+d
=Ý TnÝ
∏¿™¿i¡Av¿g¿
±…Ê√r¸Ai¿ƒ∞Ë ™…∆z¿Æ£…√ •¿z¿™¿≈ πÐg¡AP¿™¡Vz¿ƒð Cz¿£¿þ ëaí¨ƒAz¿ ∏¿∆a∏¿ƒv…€√™….
T1 = a
T2= a+d
T3=Ý T2+dÝ =(a+d)+d = a+2d = a + (3-1)d
T4=Ý T3+dÝ =(a+2d)+d =a+3d= a+(4-1)d
Tn = ÝTn-1+d = a+(n-1)d.ÝÝÝÝ d= (TnÝ
-a)/(n-1)
∏¿™¿i¡Av¿g¿ ±…Ê√r¸Ai¿ƒ
∏¡™¿i¡£¿Â •¿z¿: Tn = a+(n-1)d
∏¿™¿i¡Av¿g¿ ±…Ê√r¸Ai¿ƒ ∏¡™¿i¡£¿Âg¿∆•¿: {a, a+d, a+2d,a+3d Ö,
a+(n-1)d}
1.8.3 ∏¿™¿ƒ∏…ÂÝ
1 : Sn = 5n2+3n Dz¿g… ∏¿™¿i¡Av¿g¿ ±…Ê√r¸Ai¿ƒ£¿ƒþ ßg…¨ƒj.
•¿j∫¡g¿:
Sn-1 = 5(n-1)2+3(n-1)
= 5(n2 -2n+1) +3n-3
Ý= 5n2-10n+5+3n-3
Ý= 5n2-7n+2
Tn= Sn-
Sn-1
ÝÝÝ = (5n2+3n)
ñ(5n2-7n+2)
ÝÝ = 10n-2
![]() T1 = 8
T1 = 8
![]() T2 Ý=18
T2 Ý=18
![]() T3 Ý=28
T3 Ý=28
∏¿™¿i¡Av¿g¿ ±…Ê√r¸: Ý{8,18,28Ö..}
v¡º…:
ÝS3 = T1 + T2 +
T3 =8+18+28 = 54
Sn
= 5n2+3n
ÝÝÝ = 5*32+3*3
ÝÝÝ = 54
1.8.3 ∏¿™¿ƒ∏…ÂÝ
2Ý : MAz¿ƒ ∏¿™¿i¡Av¿g¿ ±…Ê√r¸Ai¿ƒ∞Ë T10 =20ÝÝÝ T20Ý =10 Dz¿g…Ý T30Ý P¿Aq¿ƒªr.
•¿j∫¡g¿:
™…∆z¿Æƒ a
™¿ƒv¿ƒ€ dU¿º¿£¿ƒþ
P¿Aq¿ƒªrAi¿ƒ®…√P¿ƒ.
Tn = a+(n-1)d
T10 = a+(10-1)d
= a+9d
Dz¿g…,
T10= 20 ý z¿v¿€
![]() a+9d=20: a=20-9dÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝ ====ý(1)
a+9d=20: a=20-9dÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝ ====ý(1)
T20 =
a+(20-1)d = a+19dÝ ====ý(2)
Dz¿g…,
ÝT20=
10
(1) ™¿ƒv¿ƒ€ (2)jAz¿,
T20 = a+19dÝ
Ý=20-9d+19d =10
Ý=20+10d =10
ÝÝÝÝ 10d =(10-20)= -10
ÝÝÝÝÝÝÝ Ýd = -1
(1)jAz¿,
ÝÝÝÝÝÝ a =20-9d
Ý = 20+9 =29
![]() ÝT30Ý
= a+(30-1)d
ÝT30Ý
= a+(30-1)d
ÝÝÝÝÝÝÝÝÝ = 29+29*(-1) = 29-29 =0
v¡º…:
T10 =29+9*(-1)=20
T20 =29+19*(-1)=10
1.8.3 ∏¿™¿ƒ∏… 3: 5£…√ ™¿ƒv¿ƒ€ 10£…√Ý •¿z¿U¿º¿ C£¿ƒ•¡v¿ 1:2 DVz¿ƒð,
ÝT12 =36 DVg¿ƒ™¿ ∏¿™¿i¡Av¿g¿ ±…Ê√r¸Ai¿ƒ£¿ƒþ ßg…¨ƒj.
•¿j∫¡g¿:
T5 : T10 =
1:2 (i.e T5 /T10 =1/2) ý z¿v¿€
![]() Ý2T5 = T10
Ý2T5 = T10
2(a+4d) = (a+9d)
2a+8d = a+9d
ÝÝÝÝÝÝÝÝ a=d.
T12 =36ý z¿v¿€
a+ 11d = 36
a=d Dz¿ðjAz¿, Ý12d =36
ÝÝÝÝÝÝ d=3
a=d
Dz¿ðjAz¿, Ýa=3
∏¿™¿i¡Av¿g¿ ±…Ê√r¸:
= 3,6,9,12Ö
v¡º…:
T5 = 15, T10
=30, 1:2 z¿v¿€ C£¿ƒ•¡v¿.
1.8.3 ∏¿™¿ƒ∏… 4: ™…∆v¿€15 ™¿ƒv¿ƒ€ U¿ƒtÆßÞ 105
DVg¿ƒ™¿ ∏¿™¿i¡Av¿g¿ ±…Ê√r¸Ai¿ƒ ™¿ƒ∆g¿ƒ •¿z¿U¿º¿£¿ƒþ
P¿Aq¿ƒªr¨ƒj.
•¿j∫¡g¿:
™¿ƒzs¿Âz¿ •¿z¿ a DVg¿∞.
™…∆z¿Æ •¿z¿: a-d
3£…√ •¿z¿: a+d.
™¿ƒ∆g¿ƒ •¿z¿U¿º¿
™…∆v¿€= (a-d)+a+(a+d ) = 3a = 15
Ý a = 5.
™¿ƒ∆g¿ƒ •¿z¿U¿º¿
U¿ƒtÆßÞ = (a-d)*a*(a+d) = a*(a2-d2)
=105
![]() a*(a2-d2)
=105
a*(a2-d2)
=105
ÝÝÝ 5(52-d2) = 105
ÝÝÝÝÝ (25-d2) = 21
Ý -d2 = 21-25
ÝÝÝ -d2= -4
ÝÝÝÝ d2= 4
ÝÝÝÝ d =![]()
∏¿™¿i¡Av¿g¿ ±…Ê√r¸Ai¿ƒ
•¿z¿U¿º¿ƒ: 3,5,7 Cx¿™¡ 7,5,3
v¡º…: 3,5,7 E™¿≈U¿º¿ ™…∆v¿€ 15,
U¿ƒtÆßÞ: 105.
1.8.4 ∏¿™¿i¡Av¿g¿ ±…Ê√t¬Ai¿ƒ •¿z¿U¿º¿ ™…∆v¿€(Summation of arithmetic
series):
FU¿ £¡™¿≈ F
Czs¿ÂAi¿ƒ£¿z¿ Dg¿A®s¿z¿∞Ë £…∆√rz¿ ∏¿™¿ƒ∏…ÂAi¿ƒ ßU…Œ Z¿a∏¿ƒ™¡.
1.8.4 ∏¿™¿ƒ∏… 1 : §√™¿≈ §™¿ƒ‰ ∏…þ√ªv¿§Az¿ g¿∆.
10,000 Ý∏¡Æ
•¿q…¢¢ð√g…Az¿ƒ ®s¡´∏¿ƒ™¡ ™¿ƒv¿ƒ€ ¢£¿A•¿Êw ∏¿ÈÆý ∏¿ÈÆý ∫¿t™¿£¿ƒþ ªAz¿P…Ã
P…∆q¿ƒ™¿ v¿P¿P…à §√™¿≈ M¶ý¢ð√j. DU¿ §™¿ƒU… Jg¿q¿ƒ DAi…ƒÃU¿Ω™….
1. §√™¿≈ ¢£¿P…∆ÃAz¿ƒ g¿∆•¡¨ƒAi¿ƒAv…
™¡•¡∏¿ƒ P…∆q¿Æƒ ßAi¿ƒ∏¿ƒw€√j. Ez¿P…à §™¿ƒ‰ ∏…þ√ªv¿ M•¿≈ýv¡€£…Ai¿ƒ ? RArv¡ EÆË.
KP…Az¿g… ∏¿A•¿«t ∏¡Æ w√j∏¿Æƒ ∏¿ƒ™¿i¡g¿ƒ 28 ™¿µ¿U¿º¿ƒ ®…√P¿ƒ.
(![]() =28).
=28).
2.
§√™¿≈
•¿Êw√¢£¿ ¢£¿z¿ P¿Ê™¿ƒ∏¿AS…ÂAi¿ƒµ¿ƒ÷ g¿∆•¡¨ƒU¿º¿£¿ƒþ P…∆q¿ƒw€√g…Az¿ƒ ®s¡´∏¿ƒ™¡.(1 £…√ ¢£¿ 1 g¿∆. 2£…√ ¢£¿ 2 g¿∆, 3£…√ ¢£¿ 3 g¿∆. . . . . . ª√U…) P…∆q¿ƒv¡€
∫…∆√U¿Æƒ §√™¿≈ M•¿≈ýw€√g¡ ? RArv¡ ®…√q¿ ñ KP… £…∆√q¿ƒ™¡:
2£…√ DAi…ƒÃ
ËAi¿ƒAv… ݧ√™¿≈ 10 ¢£¿U¿º¿∞Ë P…∆l÷ ∫¿t Jµ¡÷U¿ƒv¿€z…?
10 ¢£¿U¿º¿∞Ë
P…∆l÷ Mlƒ÷ ∫¿t = 1+2+3+4+5+6+7+8+9+10 = 55g¿∆.
∫¡U¡z¿g… 100
¢£¿U¿º¿∞Ë P…∆l÷ ∫¿t Jµ¿ƒ÷? Ez¿£¿þ ∏¿AS…ÂU¿º¿
™…∆v¿€¢Az¿ P¿Aq¿ƒªrAi¿ƒ®…√P¿ƒ.
Dz¿ðjAz¿, FU¿ ™…∆z¿Æ ëní
∏¡È®s¡´P¿ ∏¿AS…ÂU¿º¿ ™…∆v¿€™¿£¿ƒþ P¿Aq¿ƒªrAi¿ƒƒ™¿
∏¿∆v¿Ê K£¿ƒ JAz¿ƒ wΩAi¿ƒƒ™¡.
{T} = {1,2,3ÖÖn}
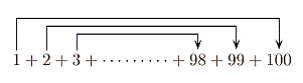
ÝÝ Sn Ý= 1 ÝÝÝÝ+ÝÝÝ 2Ý +ÝÝ 3 ÝÖÖÖÖ.+(n-2)+
(n-1) +n(n •¿z¿U¿Ω™…)
+ Sn Ý=Ý nÝÝÝ +(n-1)+(n-2) ÖÝÝÝÝÝÝÝÝÝÝÝÝÝ +Ý
3Ý
+ÝÝ 2ÝÝÝÝ +1(wg¿ƒVπ
ßg…¢z…)
==================================
≠≠≠≠≠≠≠≠≠≠≠≠≠≠≠≠≠≠≠≠≠≠2Sn=
(n+1)+(n+1)+(n+1)ÝÝÝ
Ö..ÝÝÝ .+(n+1)+(n+1)+(n+1)
(n •¿z¿U¿Ω™…)
ÝÝÝÝ = n(n+1)
![]() ÝSn=
ÝSn= ![]()
F
∏¿∆v¿Ê™¿£¿ƒþ•¿Ai…∆√Vπ, 10 ¢£¿U¿º¿∞Ë
P…∆l÷ ∫¿t™¿£¿ƒþ Ø…P¿Ã ∫¡P¿ƒ™¡:
S10 Ý=10*11/2= 55 g¿∆.
FU¿ 100
¢£¿U¿º¿∞Ë P…∆q¿ƒ™¿ Mlƒ÷ ∫¿t: S100
= 100*101/2Ý =Ý 5050g¿∆.
200 ¢£¿U¿º¿∞Ë P…∆q¿ƒ™¿ Mlƒ÷ ∫¿t: S200 =
200*201/2 =20,100g¿∆.
10,000 g¿∆.U¿º¿£¿ƒþ w√j∏¿Æƒ ®…√P¡z¿ ¢£¿U¿º¿£¿ƒþ P¿Aq¿ƒªrAi¿ƒƒ™¿ ´zs¡£¿ £¿Av¿g¿
£…∆√q¿ƒ™¡.
FU¿ ∏¿z¿ÂP…Ã: S141
= ![]() Ý=10,011
Ý=10,011
Dz¿ðjAz¿ ∏¡Æ w√j∏¿Æƒ
141 ¢£¿U¿º¿ƒ ∏¡P¿ƒ.
™…∆z¿Æ n •¿z¿U¿º¿ ™…∆v¿€ Sn£¿þ ![]() §Az¿ ∏¿∆a∏¿ƒv…€√™….
§Az¿ ∏¿∆a∏¿ƒv…€√™….
![]() =
= ![]()
™¡ÂS…Â: MAz¿ƒ ±…Ê√t¬Ai¿ƒ •¿z¿U¿º¿ƒ
∏¿™¿i¡Av¿g¿ ±…Ê√r¸Ai¿ƒ∞Ëz¿ðg…, D ±…Ê√t¬Ai¿ƒ£¿ƒþ ì∏¿™¿i¡Av¿g¿
±…Ê√t¬î(arithmetic series) J£¿ƒþ™¿g¿ƒ.
Gz¡: {2,5,8},Ý
{1,4,7,},Ý {3,7,11}
∏¿™¿i¡Av¿g¿ ±…Ê√r¸Ai¿ƒ ëní •¿z¿U¿º¿ ™…∆v¿€ P¿Aq¿ƒªrAi¿ƒƒ™¿≈z¿ƒ:
{AP}= {a, a+d, a+2d, a+3d
Ö.,a+(n-1)d}
Sn=
[a+(a+d)+(a+2d)+(a+3d) Ö..a+(n-1)d]
Ý = [a+a+a Ö.(n ∏¿Æ)
+d(1+2+3+ ÖÖ. (n-1)]
= na+d[![]() ]
]
na+ ![]() ÝÝ(
ÝÝ(![]() =
= ![]() Ý∏¿∆v¿Êz¿∞Ë n ßz¿Æƒ (n-1) G•¿Ai…∆√Vπ)
Ý∏¿∆v¿Êz¿∞Ë n ßz¿Æƒ (n-1) G•¿Ai…∆√Vπ)
Sn = na+ ![]() ÝÝ=
ÝÝ= ![]() Ý= n*(
Ý= n*(![]() )
)
= n*(![]() )=n*(
)=n*(![]() )
)
1.8.4 ∏¿™¿ƒ∏…Â2Ý
: 25 •¿z¿U¿Ωg¿ƒ™¿ MAz¿ƒ
∏¿™¿i¡Av¿g¿ ±…Ê√t¬Ai¿ƒ∞Ë ™¿ƒzs¿Âz¿ •¿z¿ 20 Dz¿g… D ±…Ê√t¬Ai¿ƒ •¿z¿U¿º¿ ™…∆v¿€ P¿Aq¿ƒªr¨ƒj.
•¿j∫¡g¿:
z¿v¿€:
n=25, T13 =20,Ý S25 P¿Aq¿ƒªrAi¿ƒ®…√P¿ƒ.
T13 = a+12d
S25 Ý= n*(a+ T25)/2= 25*(a+a+24d)/2
ÝÝÝÝÝÝ = 25*2*(a+12d)/2
ÝÝÝÝÝÝ = 25*(a+12d) = 25*20(T13 =
a+12d)
ÝÝÝÝÝÝ = 500
1.8.4 ∏¿™¿ƒ∏… 3ÝÝ
: 4 jAz¿ ®s¡U¿™¡U¿ƒ™¿ 101
jAz¿ 201 g¿
™¿g…V£¿ JÆË ∏¡È®s¡´P¿ ∏¿AS…ÂU¿º¿ ™…∆v¿€ P¿Aq¿ƒªr.
•¿j∫¡g¿:
{AP} = (104,108,112 Ö200}
Sn Ý= 104+108+112+ÖÖ
ÝÝÝÝ = 104+(104+4) + (104+8)Ö (104+96) (104, 25 ®¡j •¿ƒ£¿g¡™¿v¿£… DU¿ƒv¿€z….)(U¿™¿ƒ§π:
1£…√ •¿z¿
=104, P…∆£…Ai¿ƒ •¿z¿
200 ™¿ƒv¿ƒ€
™¿Âv¡Â∏¿ = 4)
ÝÝÝÝ = 104*25 +4(1+2+3Ö..24)
ÝÝÝÝ = (104*25) +4*(![]() )
)
ÝÝÝÝ =2600+1200=3800
1.8.4 ∏¿™¿ƒ∏… 4 : ®¡∫¿ƒß∞Ai¿ƒ KP¿≤Ø¡ ´U¿Ê∫¿´g¿ƒ™¿ ±¿Ê™¿t ®…º¿U…∆º¿P…à §√™¿≈ •¿Ê™¡∏¿
∫…∆√V¢ð√g…Az¿ƒ ®s¡´π. §√™¿≈ ™…∆z¿Æ §´ƒµ¿z¿∞Ë 23 ™…ƒn÷ƃU¿º¿£¿ƒþ ∫¿v¿ƒ€w€√j. £¿Av¿g¿ •¿Êw §´ƒµ¿z¿∞Ë §√™¿≈ ªA¢£¿
§´ƒµ¿z¿∞Ë ∫¿w€z¿ðQÃAv¿ 2 ™…ƒn÷ƃU¿º¿£¿ƒþ P¿r™…ƒ ∫¿v¿ƒ€w€√j JAz¡z¿g…, 7 §´ƒµ¿ U¿º¿∞Ë ∫¿w€z¿ Mlƒ÷ ™…ƒn÷ƃU¿º¿ ∏¿AS… P¿Aq¿ƒªr¨ƒj.
•¿j∫¡g¿:
§√™¿≈ •¿Êw√ §´ƒµ¿z¿Æ∆Ë
ªA¢£¿ §´ƒµ¿z¿∞Ë ∫¿w€z¿ðQÃAv¿ 2 ™…ƒn÷ƃ
P¿r™…ƒ ∫¿v¿ƒ€™¿≈z¿jAz¿ Cz¿ƒ ±…Ê√r¸Ai¿ƒ∞Ëz…. §√™¿≈ 7 §´ƒµ¿ P¡Æ v…U…z¿ƒP…∆Aq¿z¿ðjAz¿, ∏¿™¿i¡Av¿g¿ ±…Ê√t¬Ai¿ƒ∞Ë S7P¿Aq¿ƒ ªrAi¿ƒ®…√P¿ƒ.
{AP} = {23,21,19Ö.) ÝÝÝÝÝÝÝÝ a=23, d = -2
Sn Ý= n*(![]() )
)
![]() S7 Ý= 7* (
S7 Ý= 7* (![]() )
)
ÝÝÝÝÝÝÝ = 7*[46-12]/2
ÝÝÝÝÝ = 7*17 = 119
§√™…√ ™¿i¡r: §√™¿≈
•¿Êw™…ƒAi¿ƒ£¿þ v¿Æƒ•¿Æƒ 1000 ™…ƒn÷ƃ
∫¿v¿€®…√P¡Vz¿ðg…, Cz¿P…à ®…√P¡U¿ƒ™¿ P¡Æ™¿£¿þ P¿Aq¿ƒªr¨ƒj.
1.8.4 ∏¿™¿ƒ∏…Â5:Ý §√™¿≈ MAz¿ƒ 70Q.´ƒ. z¿∆g¿z¿ ∏… P¿ØÔ g…√∏Ô £¿∞Ë ®s¡U¿™¿ª∏¿®…√P¿ƒ. ™…∆z¿Æ U¿Am…Ai¿ƒ∞Ë
U¿Am…U… 16 Q.´ƒ. ™…√U¿z¿∞Ë Z¿∞∏¿ƒw€√j.
™¿ƒƒAz… •¿Êw√ U¿Am…Ai¿ƒ∞ËAi¿ƒ∆ MAz…∆Az¿ƒ Q.´ƒ. £¿µ¿ƒ÷ ™…√U¿ P¿r™…ƒAi¿i¡z¿g…,
∏¿ýzs… ™¿ƒƒV∏¿Æƒ ®…√P¡z¿ P¡Æ P¿Aq¿ƒªr.
•¿j∫¡g¿:
§™¿ƒ‰ ∏… P¿∞£¿ ™…√U¿: (16,15,14,
Ö) MAz¿ƒ ∏¿™¿i¡Av¿g¿ ±…Ê√r¸,
Sn =70 DU¿ƒ™¿Av… n£¿þ
P¿Aq¿ƒªrAi¿ƒ®…√P¿ƒ.
E∞Ë a
=16, d = -1
Sn ÝÝ= n*(![]() )
)
= n*(![]() )
)
= n*(![]() )
)
= n*(![]() )
)
n*(![]() )Ý = 70(Mlƒ÷ z¿∆g¿: 70Q.´ƒ.)
)Ý = 70(Mlƒ÷ z¿∆g¿: 70Q.´ƒ.)
(33n-n2 ) =
2*70=140
-n2 +33n -140 =0
Ýn2 -33n +140 =0
(n-5)*(n-28) = 0
n=5 Cx¿™¡ n=28
U¿t¬v¿z¿ •¿ÊP¡g¿ £¡´∞Ë
2 Gv¿€g¿U¿º¿£¿ƒþ (5 ™¿ƒv¿ƒ€ 28) •¿q…¢z…ð√™…. Dz¿g…
Dg¿A®s¿z¿ ™…√U¿ U¿Am…U… 16Q.´ƒ.
DVz¿ƒð, U¿Am…U… MAz¿ƒ Q.´ƒ. ™…√U¿ P¿r™…ƒAi¿i¡U¿ƒ™¡U¿ ®…√P¡z¿ P¡Æ 5 U¿Am…VAv¿
∫…Z¡—U¿Æƒ ∏¡zs¿Â´ÆË(n=28 Dz¿g… ™…√U¿ Iƒt(T28=Ý -11) DU¿ƒv¿€z…).
![]() ®…√P¡z¿ P¡Æ = 5 U¿Am…U¿º¿ƒ.
®…√P¡z¿ P¡Æ = 5 U¿Am…U¿º¿ƒ.
1.8.4 ∏¿™¿ƒ∏…Â6:Ý Mß‚ g¡d£¿ƒ
™…∆z¿Æ£…Ai¿ƒ ¢£¿ 2 Ai…∆√d£¿ z¿∆g¿
∫…∆√V,±¿v¿ƒÊ´£¿ D£…U¿º¿£¿ƒþ ªrAi¿ƒÆƒ 7
¢£¿U¿º¿∞ËÝ 80 Ai…∆√d£¿U¿º¿ƒ ∫…∆√z¿g…, •¿Êw√ ¢£¿™¿« Jµ¿ƒ÷ z¿∆g¿ ∫…a—πg¿®…√P¿ƒ,
߃¢Þ™¿Av¿£…√ ∫…√º¿ƒ? (∞√Ø¡™¿w ±…∆Ë√P¿ 126)
•¿j∫¡g¿:
g¡d£¿ƒ P¿Ê´ƒπz¿ z¿∆g¿
MAz¿ƒ ∏¿™¿i¡Av¿g¿ ±…Ê√r¸,
Sn =70 DU¿ƒ™¿Av… d £¿þ
P¿Aq¿ƒªrAi¿ƒ®…√P¿ƒ.
E∞Ë a
=2, n = 7
Sn ÝÝ= n*(![]() )
)
= 7*(![]() )
)
= 7*(![]() )
)
= 7*(2+3d) = 80
![]() Ý2+3d = 80/7
Ý2+3d = 80/7
![]() Ý3d = (80/7)-2 = (66/7)
Ý3d = (80/7)-2 = (66/7)
g¡d£¿ƒ •¿Êw√ ¢£¿™¿« 22/7 Ai…∆√d£¿ z¿∆g¿™¿£¿ƒþ ∫…a—∏¿®…√P¿ƒ.
1.8.4 ∏¿™¿ƒ∏…Â7:Ý Mß‚£¿ƒÝ ™…∆z¿Æ£…Ai¿ƒ ¢£¿ 3 •¿ÆË zs¡£¿Â™¿£¿ƒþ z¡£¿ ™¿i¡r, •¿Êw√ ¢£¿™¿«Ý 2
•¿ÆËU¿º¿£¿ƒþ ∫…a—∏¿ƒv¡€ ∫…∆√z¿g… 360
•¿ÆËU¿º¿£¿ƒþ Jµ¿ƒ÷ ¢£¿U¿º¿∞Ë z¡£¿ ™¿i¡q¿ƒv¡€£…. ∞√Ø¡™¿wAi…ƒ√ ®…√U¿ ∫…√º¿ƒ. (∞√Ø¡™¿w ±…∆Ë√P¿ 124)
•¿j∫¡g¿:
z¡£¿ ™¿i¡rz¿ zs¡£¿Â
MAz¿ƒ ∏¿™¿i¡Av¿g¿ ±…Ê√r¸,
Sn =360 DU¿ƒ™¿Av… n £¿þ
P¿Aq¿ƒªrAi¿ƒ®…√P¿ƒ.
E∞Ë a
=3, d = 2
Sn ÝÝ= n*(![]() )
)
= n*(![]() )
)
= n*(3n+2n-2) = n(n+2)
![]() Ýn2+2n =360
Ýn2+2n =360
![]() Ýn2+2n -360
=0
Ýn2+2n -360
=0
![]() Ý(n+20)*(n-18) =0
Ý(n+20)*(n-18) =0
n=-20 ∏¡zs¿Â´Æ.ËÝ 360 •¿ÆË z¡£¿ ™¿i¡q¿Æƒ 18
¢£¿U¿º¿ƒ ®…√P¿ƒ.
1.8.5
U¿ƒu…∆√v¿€g¿
±…Ê√r¸(Geometric Progression)
(GP):
P…º¿V£¿
Gz¡∫¿g¿u…U¿º¿£¿ƒþ U¿™¿ƒ§π:
1.Ý {T}= {2,4,8,16 ÖÖ.}.Ý F ±…Ê√r¸Ai¿ƒ∞Ë •¿Êw
•¿z¿™¿« ªA¢£¿ •¿z¿z¿ Jg¿q¿g¿∂÷z….
Ai¿i¡™¿≈z…√ •¿z¿ =
2* ªA¢£¿ •¿z¿ Cx¿™¡ = 1/2* ™¿ƒƒA¢£¿ •¿z¿
•¿z¿U¿º¿ £¿q¿ƒ´£¿
C£¿ƒ•¡v¿= 1:2.
2. {T}=
{27,9,3,1 ÖÖ.}.Ý F
±…Ê√r¸Ai¿ƒ∞Ë •¿Êw •¿z¿™¿« ªA¢£¿ •¿z¿z¿ 1/3g¿∂÷z….Ai¿i¡™¿≈z…√ •¿z¿ = 1/3* ªA¢£¿
•¿z¿ Cx¿™¡ Ý™¿ƒƒA¢£¿ •¿z¿ = 3* ªA¢£¿
•¿z¿.Ý •¿z¿U¿º¿ £¿q¿ƒ´£¿ C£¿ƒ•¡v¿
=3:1
™¡ÂS…Â: ±…Ê√r¸Ai¿ƒ Ai¿i¡™¿≈z…√ MAz¿ƒ •¿z¿ ™¿ƒv¿ƒ€ Cz¿g¿ ªA¢£¿ •¿z¿U¿º¿ C£¿ƒ•¡v¿
MAz¿ƒ πÐg¡AP¿™¡Vz¿ðg…, Cz¿£¿ƒþ ìU¿ƒu…∆√v¿€g¿ ±…Ê√r¸î(Geometric
Progression)(GP)í J£¿ƒþv¡€g…. F πÐg¡AP¿™¿£¿ƒþ ë∏¡™¿i¡£¿Â
C£¿ƒ•¡v¿í J£¿ƒþv¡€g… ™¿ƒv¿ƒ€ Cz¿£¿þ ërí
§Az¿ ∏¿∆a∏¿ƒv…€√™….
MAz¿ƒ GPAi¿ƒ∞Ë TnÝ /Tn-1
= πÐg¡AP¿
1£…√ Gz¡. z¿∞Ë T3ÝÝ /T2=![]() =2 ÝÝÝÝÝÝ 2£…√ Gz¡. z¿∞Ë T3ÝÝ /T2=
=2 ÝÝÝÝÝÝ 2£…√ Gz¡. z¿∞Ë T3ÝÝ /T2=![]() = 1/3
= 1/3
MAz¿ƒ U¿ƒu…∆√v¿€g¿
±…Ê√r¸Ai¿ƒ∞Ë ™…∆z¿Æ •¿z¿ T1 = a ∏¡™¿i¡£¿Â C£¿ƒ•¡v¿ ërí
Dz¿g…,
T2= T1*r=
ar(2-1)
T3= T2*r=
ar*r =ar2= ar(3-1)
T4= T3*r=
ar2*r = ar3= ar(4-1)
∏¡™¿i¡£¿Â™¡V, Tn= ar(n-1) ;ÝÝÝ Tn= ar(n-1
= ar(n-2)*r=Tn-1*r
U¿ƒu…∆√v¿€g¿ ±…Ê√r¸
∏¡™¿i¡£¿Âg¿∆•¿:- {a, ar, ar2, ar3 ÖÖÖ..
ar(n-1)}Ý ofÝ GP.
1.8.5 ∏¿™¿ƒ∏… 1 :Ý MAz¿ƒ U¿ƒu…∆√v¿€g¿
±…Ê√r¸Ai¿ƒ∞Ë 7£…√ •¿z¿™¿≈ 4£…√ •¿z¿z¿ JAlg¿∂÷z… ™¿ƒv¿ƒ€Ý 5£…√ •¿z¿ 12 Dz¿g…, D ±…Ê√r¸Ai¿ƒ£¿ƒþ ßg…¨ƒj.
•¿j∫¡g¿:
Tn = arn-1
![]() ÝT7=a r6
,Ý T4=a r3 Dz¿g… T7= 8T4 ý
z¿v¿€
ÝT7=a r6
,Ý T4=a r3 Dz¿g… T7= 8T4 ý
z¿v¿€
![]() Ýa r6= 8 ar3
Ýa r6= 8 ar3
![]() Ýr3= 8
Ýr3= 8
![]() Ýr=2
Ýr=2
T5=a r4
ÝÝÝ = a 24=16a =12 (z¿v¿€)
![]() Ýa =
Ýa = ![]() Ý=
Ý=![]()
z¿v¿€ U¿ƒu…∆√v¿€g¿
±…Ê√r¸ = {![]() ,
, ![]() *2,
*2, ![]() *22 ,
*22 , ![]() *23Ö.} = {3/4, 3/2,3,6Ö}
*23Ö.} = {3/4, 3/2,3,6Ö}
U¿ƒu…∆√v¿€g¿ ±…Ê√r¸Ai¿ƒ n •¿z¿U¿º¿ ™…∆v¿€ P¿Aq¿ƒ ªrAi¿ƒƒ™¿≈z¿ƒ:
= {a, ar, ar2,
ar3 ÖÖÖ.. ar(n-1)}(n terms)
ÝÝÝÝÝÝÝÝÝÝÝ (1)ÝÝÝÝÝÝÝ Sn= a +ar+ar2+ ar3
ÖÖÖ.. +ar(n-1)Ý ÝÝÝ
™…ƒ√∞£¿
∏¿´ƒ√P¿g¿t™¿£¿ƒþ ërí §Az¿ U¿ƒt¬πz¡U¿,ÝÝÝÝÝÝÝÝÝÝÝ
Ý (2)ÝÝÝÝÝÝÝ
rSn=ÝÝÝÝÝÝ ar+ar2+
ar3 ÖÖÝÝÝÝÝÝ +ar(n-1)+
arn
∏¿.(2)
jAz¿ (1)£¿þ
P¿º…z¡U¿,
Sn- rSn=a-
arn
Sn(1-r) =a(1- rn)
Sn=
a (1- rn)Ý / (1-r)ÝÝ -----ý
r <1 Dz¡U¿,
ÝÝÝ
= -a (1- rn) /-(1-r) (CA±¿ ™¿ƒv¿ƒ€ b…√z¿U¿º…g¿q¿£¿∆þ -1jAz¿ U¿ƒt¬π)
ÝÝÝ
=Ý a ( rn-1) /Ý (r-1)ÝÝÝÝÝ
-----ý
r >1 Dz¡U¿,
r U…
Ai¿i¡™¿≈z…Ø¡Ë ®…Ø… Eg¿ß∫¿ƒz¿ƒ? ( r=1, r>1,r<1)
1) r=1 Dz¡U¿, GP = {a ,a,a.a,aÖ.}
2) r<1 Dz¡U¿,
Gz¡∫¿g¿u…U…, r
= ![]() Ý= 0.9 Dz¡U¿, n Cw z…∆q¿ÿ ∏¿AS… Dz¡U¿, G
K£¡U¿ƒv¿€z…?
Ý= 0.9 Dz¡U¿, n Cw z…∆q¿ÿ ∏¿AS… Dz¡U¿, G
K£¡U¿ƒv¿€z…?
|
r2= |
0.81 |
|
r4= |
0.66 |
|
r8= |
0.43 |
|
r16= |
0.19 |
|
r64= |
0.0012 |
F j√wAi¿i¡V, n£¿ ®…Ø… Cw ∫…Z¡—z¡U¿, rn ∏…∆£…þAi¿ƒ£¿ƒþ ∏¿´ƒ√¶∏¿ƒv¿€z…. (we say rnÝ approaches 0).
Cz…√j√w r£¿ ®…Ø… 1g¿ ∏¿´ƒ√•¿ Ý(999/1000)
Dz¡U¿ P¿∆q¡ ª√U… DU¿ƒv¿€z….
r<1 Dz¡U¿ U¿ƒu…∆√v¿€g¿ ±…Ê√r¸Ai¿ƒ
C£¿Av¿ •¿z¿U¿º¿ ™…∆v¿€ Sn= a (1- rn)
/ (1-r)Ý ====Ë
Sinfinity = ![]() =
= ![]()
MAz¿ƒ
U¿ƒu…∆√v¿€g¿ ±…Ê√r¸Ai¿ƒ∞Ë S2n/ Sn =
rn+1 JAz¿ƒ ∏¡¢¸π.
S2n/ Sn =
[a(1- r2n)/(1-r)]/ [a(1- rn)/(1-r)]
ÝÝÝÝÝÝÝÝÝÝ = [a(1- r2n)*(1-r)]/[a
(1- rn)*(1-r)]
ÝÝÝÝÝÝÝÝÝÝ = (1- r2n)/ (1- rn)
ÝÝÝÝÝÝÝÝÝÝ = (1- rn) (1+ rn)/
(1- rn)ÝÝÝ ===ý (a2-
b2) = (a-b)*(a+b) , r2n= (rn)2
ÝÝÝÝÝÝÝÝÝÝ =Ý
(1+ rn)
1.8.5 ∏¿™¿ƒ∏… 2 :Ý F •¿j´ƒv¿ ±…Ê√t¬Ai¿ƒ
™…∆v¿€ P¿Aq¿ƒªr: { 1,0.1,0.01,0.001,Ö. (0.1)9} (U¿™¿ƒ§π: ±…Ê√t¬Ai¿ƒ∞Ë Ý9 •¿z¿U¿º¿ÆË. 10•¿z¿U¿Ω™….)
•¿j∫¡g¿:
a=1, r=1/10
Sn = a (1- rn)
/ (1-r)Ý
![]() S10 = 1(1- (1/10)10 ) / (1-1/10)
S10 = 1(1- (1/10)10 ) / (1-1/10)
ÝÝÝÝÝ =Ý
[(1010 -1)/1010]/(9/10)
ÝÝÝÝÝ =Ý (1010 -1)/(9*109)
1.8.5 ∏¿™¿ƒ∏… 3 : S10:Ý S5=Ý 33:1, T6= 32 Dz¿g… D U¿ƒu…∆√v¿€g¿ ±…Ê√r¸Ai¿ƒ£¿þ ßg…¨ƒj.
•¿j∫¡g¿:
GPAi¿ƒ∞Ë
S10/ ÝS5 = [a(r10-1)/(r-1)]/
[a(r5-1)/(r-1)]
ÝÝÝÝÝÝÝÝÝÝ = (r10-1)/ (r5-1)
ÝÝÝÝÝÝÝÝÝÝ =Ý
(r5+1)Ý =====ý U¿™¿ƒ§π: {(a2-
b2) = (a-b)*(a+b) ™¿ƒv¿ƒ€Ý r10= (r5)2}
ÝDz¿g… S10/Ý S5 =Ý 33 JAz¿ƒ P…∆n÷z….
ÝÝÝÝÝÝÝÝ ![]() (r5+1) =33
(r5+1) =33
![]() Ýr5 =33-1=32ÝÝ
Ýr5 =33-1=32ÝÝ ![]() Ýr =2
Ýr =2
Tn = arn-1
T6 = a25
ÝÝÝÝÝÝÝ =
32(given)
![]() a=1
a=1
{GP} = (1, 2, 4, 8, 16,
32,Ö}
1.8.5 ∏¿™¿ƒ∏… 4 :Ý §√™¿≈ §™¿ƒ‰
∫¿ƒlƒ÷∫¿ß‚™¿£¿ƒþ P…Æ™¿≈ ±¡Ø…U¿º¿ ™¿ƒP¿ÃΩU… πªwAr ∫¿AZ¿ƒ™¿ ™¿ƒ∆ÆP¿
DZ¿j∏¿®…√P…Az¿ƒ §zs¿j∏¿ƒw€√j.ª√U… ∫¿AZ¿ƒ™¡U¿, 1 •¡ÂP…√mÔ §Az¿ Dg¿A©¸π
•¿Êw ±¡Ø…U¿∆ Cz¿g¿ ªA¢£¿ ±¡Ø…U… P…∆l÷ •¡ÂP…√lƒU¿º¿, 4
g¿µ¿ƒ÷ •¡ÂP…√lƒU¿º¿£¿ƒþ P…∆q¿ƒw€√j. §™¿ƒ‰∞Ë
341 πªwAr •¡ÂP…√lƒU¿Ωz¿ðg…, Jµ¿ƒ÷ ±¡Ø…U¿ΩU… §√™¿≈ πªwAr
P…∆q¿ß∫¿ƒz¿ƒ?Ý
•¿j∫¡g¿:
±¡Ø…U¿ΩU… ∫¿Aaz¿ πª
wAr •¡ÂP…√lƒU¿º¿ ∏¿AS…ÂAi¿ƒƒ U¿ƒu…∆√v¿€g¿ ±…Ê√r¸Ai¿ƒ∞Ëz….
= {1,4,16,Ö.}
DU¿, a=1, r=4. Sn = 341 n=?
r >1![]() Sn = [a(rn-1)/(r-1)]
Sn = [a(rn-1)/(r-1)]
ÝÝÝÝÝ
![]() Sn = a(4n-1)/(4-1)
Sn = a(4n-1)/(4-1)
ÝÝÝÝÝÝÝÝÝÝÝÝ = 1(4n-1)/3
ÝÝÝÝÝÝÝÝÝÝÝ = 341 ýz¿v¿€
![]() Ý(4n-1)
= 3Sn = 3*341=1023
Ý(4n-1)
= 3Sn = 3*341=1023
Ý4n= 1024
![]() Ý n =5
Ý n =5
§√™¿≈ 5
±¡Ø…U¿ΩU… πª wAr ∫¿AZ¿ß∫¿ƒz¿ƒ
1.8.5 ∏¿™¿ƒ∏… 5:Ý Mß‚£¿ƒÝ ™…∆z¿Æ£…Ai¿ƒ ¢£¿ 2 ™¿g¡lP¿ z¡£¿ ™¿i¡r, •¿Êw√ ¢£¿™¿« ªA¢£¿ ¢£¿ P…∆l÷z¿ðg¿ Jg¿q¿g¿µ¿ƒ÷
P…∆q¿ƒv¡€ ∫…∆√z¿g…, MAz¿ƒ wAU¿º¿∞Ë Jµ¿ƒ÷Ý
z¡£¿ ™¿i¡q¿ƒv¡€£…. ∞√Ø¡™¿wAi…ƒ√ ®…√U¿ ∫…√º¿ƒ. (∞√Ø¡™¿w
±…∆Ë√P¿ 130)
•¿j∫¡g¿:
z¡£¿ ™¿i¡rz¿
∏¿AS…ÂAi¿ƒƒ U¿ƒu…∆√v¿€g¿ ±…Ê√r¸Ai¿ƒ∞Ëz….
= {2,4,8,16,,Ö.}
DU¿, a=2, r=2, n=30
![]() Sn = [a(rn-1)/(r-1)]
Sn = [a(rn-1)/(r-1)]
![]() Sn = 2(230-1)/(2-1)
Sn = 2(230-1)/(2-1)
ÝÝÝÝÝÝÝÝÝ
= 2(10243-1)ÝÝÝ ( ![]() Ý230 ={210}3=10243
Ý230 ={210}3=10243
ÝÝÝÝÝÝÝÝÝÝÝ = 2147483646
1.8.6
∫¿g¡v¿‰P¿
±…Ê√r¸(Harmonic Progression):
F P…º¿V£¿
±…Ê√r¸U¿º¿£¿ƒþ U¿™¿ƒ§π:-
{![]() ,
, ![]() Ý,
Ý, ![]() Ý,
Ý,![]() Ö}
Ö}
{![]() ,
,![]() ,
,![]() Ö}
Ö}
™…ƒ√∞£¿ ±…Ê√r¸U¿º¿
•¿z¿U¿º¿ ´Ø…∆√™¿ƒ™¿£¿ƒþ ßg…z¡U¿,
{ 3, 6, 9 12Ö} Ez¿ƒ MAz¿ƒ ∏¿™¿i¡Av¿g¿ ±…Ê√r¸ (∏¿™¿ƒ∏…Â1.8.3.3)
{8,18,28Ö.} Ez¿ƒ MAz¿ƒ ∏¿™¿i¡Av¿g¿ ±…Ê√r¸ (∏¿™¿ƒ∏…Â
1.8.3.1)
™¡ÂS…Â:MAz¿ƒ ±…Ê√r¸Ai¿ƒ •¿z¿U¿º¿ƒ
E£…∆þAz¿ƒ ∏¿™¿i¡Av¿g¿ ±…Ê√r¸Ai¿ƒ •¿z¿U¿º¿ ´Ø…∆√™¿ƒU¿º¡Vz¿ðg…, D ±…Ê√r¸Ai¿ƒ£¿ƒþ ë∫¿g¡v¿‰P¿ ±…Ê√r¸í(Harmonic progression) J£¿ƒþ™¿g¿ƒ.
Cz¿£¿þ Ýë{HP}í Ai…ƒAv¿Æ∆ ∏¿∆a∏¿ƒ™¿g¿ƒ.
∏¿™¿i¡Av¿g¿ ±…Ê√r¸Ai¿ƒ{AP} ∏¡™¿i¡£¿Â •¿z¿ = Tn =a+(n-1)d
![]() {HP} Ai¿ƒ
∏¡™¿i¡£¿Â •¿z¿ =
{HP} Ai¿ƒ
∏¡™¿i¡£¿Â •¿z¿ = ![]()
{HP}= {![]() ,
, ![]() ,
, ![]() ,
, ![]() ÖÖ.
ÖÖ. ![]() }
}
U¿™¿ƒ§π:
∫¿g¡v¿‰P¿ ±…Ê√r¸Ai¿ƒ •¿z¿U¿º¿ ™…∆v¿€ Sn
P¿Aq¿ƒªrAi¿ƒƒ™¿ Ai¿i¡™¿≈z…√ ∏¿∆v¿Ê EÆË.
1.8.6 ∏¿™¿ƒ∏… 1 : MAz¿ƒ ∫¿g¡v¿‰P¿ ±…Ê√r¸Ai¿ƒ∞Ë T4= ![]() Ý, T10=
Ý, T10= ![]() ÝDz¿g… T19
P¿Aq¿ƒªr¨ƒj.
ÝDz¿g… T19
P¿Aq¿ƒªr¨ƒj.
•¿j∫¡g¿:
∫¿g¡v¿‰P¿ ±…Ê√r¸Ai¿ƒ∞Ë
Tn= ![]()
![]() ÝT4=
ÝT4= ![]() Ý=
Ý= ![]() Ý(z¿v¿€)
Ý(z¿v¿€)
![]() T4=
T4= ![]() =
= ![]()
![]() Ý a+3d
=12Ý ==========ý(1)
Ý a+3d
=12Ý ==========ý(1)
T10= ![]() Ý=
Ý= ![]() ( z¿v¿€)
( z¿v¿€)
![]() Ýa+9d
=42Ý ==========ý (2)
Ýa+9d
=42Ý ==========ý (2)
Ý(1) £¿þ (2)
jAz¿ P¿º…z¡U¿,
a+9d-(a+3d) =42-12
![]() Ý6d = 30
Ý6d = 30
![]() Ýd =5
Ýd =5
1 g¿∞Ë d
Ai¿ƒ ®…Ø… 5£¿þ
Dz…√≤π,
a+3*5 =12
a = (12-15) = -3
T19= ![]()
ÝÝÝÝ = ![]()
ÝÝÝÝ = ![]()
1.8.7
∏¿™¿i¡Av¿g¿,
U¿ƒu…∆√v¿€g¿ ™¿ƒv¿ƒ€ ∫¿g¡v¿‰P¿ ™¿i¡zs¿ÂU¿º¿ƒ(Arithmetic,
Geometric and Harmonic means) (AM,GM and HM):
™¡ÂS…Â: a,
A ™¿ƒv¿ƒ€ bU¿º¿ƒ
ë∏¿™¿i¡Av¿g¿ ±…Ê√r¸Ai¿ƒí Ý™¿ƒ∆g¿ƒ •¿z¿U¿º¡z¿g…, a
™¿ƒv¿ƒ€ bU¿º¿
£¿q¿ƒ´£¿ ∏¿™¿i¡Av¿g¿ ™¿i¡zs¿Â {Arithmetic Mean (AM)} ëAí DVg¿ƒv¿€z….
a, A ™¿ƒv¿ƒ€ bU¿º¿ƒ ∏¿™¿i¡Av¿g¿
±…Ê√r¸Ai¿ƒ •¿z¿U¿º¿ƒ.
A-a =b-A( πÐg¿ Cx¿™¡ ∏¡™¿i¡£¿Â ™¿Âv¡Â∏¿)
2A = a+b
A = ![]() Ý
Ý
™¡ÂS…Â: a,
G ™¿ƒv¿ƒ€ bU¿º¿ƒ
ëU¿ƒu…∆√v¿€g¿ ±…Ê√r¸Ai¿ƒí Ý™¿ƒ∆g¿ƒ •¿z¿U¿º¡z¿g…, a
™¿ƒv¿ƒ€ bU¿º¿
£¿q¿ƒ´£¿ U¿ƒu…∆√v¿€g¿ ™¿i¡zs¿Â{Geometric Mean (GM)}ëGí DVg¿ƒv¿€z….
a, G ™¿ƒv¿ƒ€ b U¿º¿ƒ U¿ƒu…∆√v¿€g¿
±…Ê√r¸Ai¿ƒ •¿z¿U¿º¿ƒ.
![]() Ý=
Ý=![]() ( ∏¡™¿i¡£¿Â C£¿ƒ•¡v¿)
( ∏¡™¿i¡£¿Â C£¿ƒ•¡v¿)
G2= ab
G = ![]()
™¡ÂS…Â:
a, H ™¿ƒv¿ƒ€ bU¿º¿ƒ
ë∫¿g¡v¿‰P¿ ±…Ê√r¸Ai¿ƒí ™¿ƒ∆g¿ƒ •¿z¿U¿º¡z¿g…, ëHí -
a ™¿ƒv¿ƒ€ bU¿º¿
£¿q¿ƒ´£¿ ∫¿g¡v¿‰P¿ ™¿i¡zs¿Â{Harmonic Mean (HM)}™¡Vg¿ƒv¿€z….
a, H, b ý ∫¿g¡v¿‰P¿ ±…Ê√r¸Ai¿ƒ •¿z¿U¿º¡z¿g…,
(![]() ,
,![]() ,
,![]() ) ∏¿™¿i¡Av¿g¿ ±…Ê√r¸Ai¿i¡Vg¿®…√P¿ƒ.
) ∏¿™¿i¡Av¿g¿ ±…Ê√r¸Ai¿i¡Vg¿®…√P¿ƒ.
Dz¿ðjAz¿
![]() -
-![]() =
= ![]() Ý-
Ý-![]() ( ∏¡™¿i¡£¿Â ™¿Âv¡Â∏¿)
( ∏¡™¿i¡£¿Â ™¿Âv¡Â∏¿)
![]() Ý=
Ý= ![]() +
+![]()
ÝÝÝÝÝ = ![]()
![]() Ý2ab =H(a+b)
Ý2ab =H(a+b)
![]() ÝH =
ÝH = ![]()
1.8.7 •¿Ê™…ƒ√Ai¿ƒ: A, G ™¿ƒv¿ƒ€ H U¿º¿ƒ Jg¿q¿ƒ zs¿£¿
∏¿AS…ÂU¿º¿Ý £¿q¿ƒ´£¿ ∏¿™¿i¡Av¿g¿ ™¿i¡zs¿Â
(AM) U¿ƒu…∆√v¿€g¿ ™¿i¡zs¿Â (GM) ™¿ƒv¿ƒ€ ∫¿g¡v¿‰P¿ ™¿i¡zs¿Â (HM)U¿º¡z¿g…,
A,G ™¿ƒv¿ƒ€ H U¿º¿ƒ
U¿ƒu…∆√v¿€g¿ ±…Ê√r¸Ai¿ƒ∞Ë™… JAz¿ƒ ∏¡¢¸π.
∏¡¢¸∏¿®…√P¡z¿ƒð: ÝG/A =H/G (∏¡™¿i¡£¿Â
C£¿ƒ•¡v¿)
FU¿, (AM)
A = ![]() ÝÝ(GM) G =
ÝÝ(GM) G = ![]()
(HM) H = ![]()
A*H = ![]() *
*![]() = ab= (
= ab= (![]() )2= G2
)2= G2
Cx¿™¡ ÝÝH/G = G/AÝ Dz¿ðjAz¿, A,G,
H U¿º¿ƒ U¿ƒu…∆√v¿€g¿ ±…Ê√r¸Ai¿ƒ∞Ë™….
U¿™¿ƒ§π: Ai¿i¡™¿≈z…√ Jg¿q¿ƒ zs¿£¿ ∏¿AS…ÂU¿ΩU…, A![]() G
G![]() H DVg¿ƒv¿€z….( (a+b)2 £¿ ∏¿∆v¿Ê G•¿Ai…∆√Vπ ∏¡¢¸π)
H DVg¿ƒv¿€z….( (a+b)2 £¿ ∏¿∆v¿Ê G•¿Ai…∆√Vπ ∏¡¢¸π)
1.8 P¿∞P…Ai¿ƒ ∏¡g¡A±¿
|
P¿Ê.∏¿A. |
£…£¿¶q¿®…√P¡z¿ CA±¿U¿º¿ƒ |
|
1 |
{AP}=
{a, a+d, a+2d,a+3d Ö..a+(n-1)d} ∏¿™¿i¡Av¿g¿ ±…Ê√r¸Ai¿ƒ ∏¡™¿i¡£¿Â •¿z¿: Tn=Ý a+(n-1)d |
|
2 |
|
|
3 |
∏¿™¿i¡Av¿g¿
±…Ê√r¸Ai¿ƒ∞Ë Sn
Ý=Ý n*[2a+(n-1)*d]/2= n*(a+ Tn)/2 |
|
4 |
{GP} =
{a, ar, ar2, ar3 ÖÖÖ.. ar(n-1)}Ý U¿ƒu…∆√v¿€g¿ ±…Ê√r¸Ai¿ƒ
∏¡™¿i¡£¿Â •¿z¿:Tn=
Tn-1*rÝ = ar(n-1) |
|
5 |
U¿ƒu…∆√v¿€g¿
±…Ê√r¸Ai¿ƒ Sn
= a(1- rn)/(1-r)ÝÝÝÝÝÝÝ |
|
6 |
{HP}= { |
|
7 |
∏¿™¿i¡Av¿g¿
±…Ê√r¸Ai¿ƒ ∏¿™¿i¡Av¿g¿ ™¿i¡zs¿Â (AM): A= |
|
8 |
U¿ƒu…∆√v¿€g¿
±…Ê√r¸Ai¿ƒ ∏¿™¿i¡Av¿g¿ ™¿i¡zs¿Â (GM): G = |
|
9 |
∫¿g¡v¿‰P¿
±…Ê√r¸Ai¿ƒ ∏¿™¿i¡Av¿g¿ ™¿i¡zs¿Â (HM): H = |