1.9 Permutations and
Combinations:
1.9.1
Permutations
Problem :
A team has 10 players. Only six can fit into one photo frame. Manager has to be
in each of the photo session. A photographer was asked to give an estimate for all
the different combinations of photos. A photo with frame costs Rs.22. Find out
the estimate given by photographer to the Manager.
Problem :
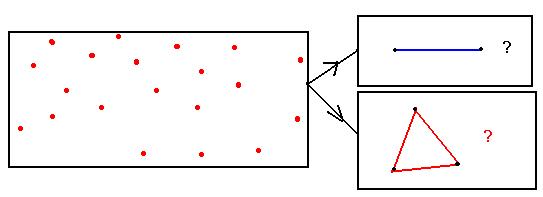
In a hexagon how many triangles can be formed?
Is it not
interesting to solve the above problems?
Introduction:
We have learnt that the sum
of 1st ‘n’ natural numbers is given by
= 1+2+3+4
…..+n =
What if we multiply these
natural numbers instead of adding them?
1*2=2
1*2*3 =6
1*2*3*4 = 24…
We use the notation n!(
called ‘n factorial’) to denote the product of ‘n; consecutive natural number from 1.
n!=
1*2*3*4….*n
What do we observe?
1! =1
2!=
1*2=2=2*1!
3!=1*2*3=6
=3*2!
4! =1*2*3*4 = 24= 4*3!
n!
= n*(n-1)*(n-2)*(n-3)*…………3*2*1=n*(n-1)!
n!
= n*(n-1)! Or n = 
1.9.1 Example1 :
Let A , B and C be students of your class . You are
asked to arrange them in rows as follows:
1. with rows of 2 students
2. with rows of 3 students
How many arrangements can
you make in each of the case?
Working:
1.9.1.1: Arrange 2
rows with two
students in each row
1.Let
us ask A to stand first. We are left with B and C. We can ask B or C to stand
behind A ( so we have 2 arrangements AB and AC)
2.Let
us ask B to stand first. We are left with A and C. We can will ask A or C to stand behind B (so
we have 2 arrangements BA and BC)
3.Let
us ask C to stand first. We are left with A and B. We can ask A or B to stand behind C (so we
have 2 arrangements CA and CB)
|
I position |
A |
B |
C |
|||
|
II
position |
B |
C |
A |
C |
A |
B |
In all we have 6(=3*2) ways
of arrangements: (AB, AC), (BA, BC), (CA, CB)
1.9.1.2: Arrange 3
rows with 3
students in each row:
1.Let
us ask A to stand first. We are left with B and C. We can ask B or C to stand behind
A( so we have 2 arrangements ABC and ACB)
2.Next
let us ask B to stand first. We are left with A and C. We can ask A or C to
stand behind B(so we have 2 arrangements BAC and BCA)
3.Next
let us ask C to stand first. We are left with B and A. We can ask A or B to
stand behind C (so we have 2 arrangements CAB and CBA)
|
I position |
A |
B |
C |
|||
|
II position |
B |
C |
A |
B |
C |
A |
|
III
position |
C |
B |
C |
C |
B |
C |
In all we have 6(=3*2) ways
of arrangements: (ABC, ACB), (BAC, BCA), (CAB, CBA)
1.9.1 Example 2:
Let us take the case of 4 students A, B, C and D in the above example. How many
different Queues can you form?
1. With Queues of 2
students
2. With Queues of 3
students
How many arrangements can
you make in each of the case?
Working:
1.9.1.2.1: Arrange
Queues of 2 students
|
I position |
A |
B |
C |
D |
||||||||
|
II position |
B |
C |
D |
A |
B |
C |
D |
A |
B |
C |
D |
A |
Totally we have 12(=4*3) ways
of arrangements (AB, AC, AD),( BA, BC, BD),( CA, CB, CD),( DA, DB, DC
1.9.1.2.2: Arrange
Queues of 3 students:
|
I position |
A |
B |
C |
D |
||||||||||||||||||||
|
II position |
B |
C |
D |
A |
B |
C |
D |
A |
B |
C |
D |
A |
||||||||||||
|
III
position |
C |
D |
B |
D |
C |
D |
B |
D |
C |
D |
B |
D |
C |
D |
B |
D |
C |
D |
B |
D |
C |
D |
B |
D |
We have:
6(=3*2) Queues with A in
the front (ABC, ABD, ACB ACD, ADB, ADC )
6 Queues with B in the
front (BAC, BAD, BCA, BCA, BDA, BDC)
6 Queues with C in the
front (CAB, CAD, CBA, CBD, CDA, CDB)
6 Queues with D in the
front (DAB, DAC, DBA, DBC, DCA, DCB)
Totally we have 24(=4*3*2)
ways arrangements
The number of arrangements
(‘permutations’) of ‘n’ things taken ‘r’ things at a time is denoted by nPr
Let us analyse
our workings:
|
Examples |
Total Number of students(n) |
Number of students in the row(r) |
Number of arrangements |
Notation |
Meaning |
|
Example
1.1 |
3 |
2 |
6 |
3P2 |
Permutation
of 3 objects taken 2 at a time |
|
Example
1.2 |
3 |
3 |
6 |
3P3 |
Permutation
of 3 objects taken 3 at a time |
|
Example
2.1 |
4 |
2 |
12 |
4P2 |
Permutation
of 4 objects taken 2 at a
time |
|
Example
2.1 |
4 |
3 |
24 |
4P3 |
Permutation
of 4objects taken 3 at a time |
Permutation is a way of
arranging objects in an orderly way.
1.9.2
Fundamental Principles of counting:
Assume that you and your
friend go to school together. Assume that there are 4 routes to go to your
friend’s house from your house and 3 routes from your friend’s house to the
school. Also, Assume that you have a pet dog ‘Jony’ which some times
follows you.
Find out how many different
routes, ‘Jony’ can
take to reach your house from the school, via your friend’s house?
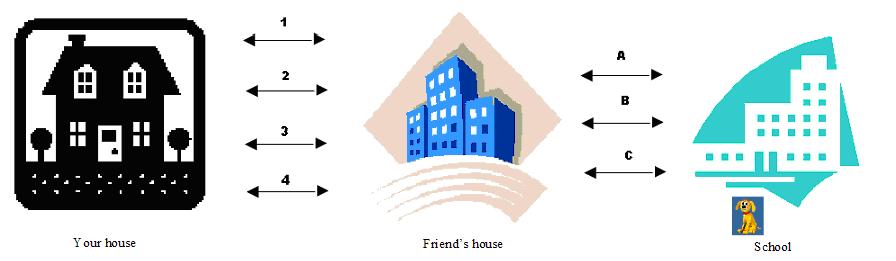
Note: There are 4 routes to
reach your friend’s house from your house and there are 3 routes to reach
school from your friend’s house.
‘Jony’ can take any of the three routes
(A or
B or
C)
from the school to reach your friends house. From your friend’ house it can
reach your house in four ways (1 or 2 or 3 or 4).
The following table lists
the different ways that ‘Jony’ can take to reach your house from the school via
your friend’s house.
|
No |
From School to friend’s house |
From friend’s house to your
house |
Route |
|
1 |
A |
1 |
A-1 |
|
2 |
2 |
A-2 |
|
|
3 |
3 |
A-3 |
|
|
4 |
4 |
A-4 |
|
|
5 |
B |
1 |
B-1 |
|
6 |
2 |
B-2 |
|
|
7 |
3 |
B-3 |
|
|
8 |
4 |
B-4 |
|
|
9 |
C |
1 |
C-1 |
|
10 |
2 |
C-2 |
|
|
11 |
3 |
C-3 |
|
|
12 |
4 |
C-4 |
‘Jony’ can chose
12(=3*4) ways of reaching your house from the school.
Similarly there are 12 (=4*3) ways of reaching
school from your house.
In summary, if an
activity can be done in ‘m’ ways and another activity is done in ’n’ ways then
the 2 activities together can be done in (m*n) ways.
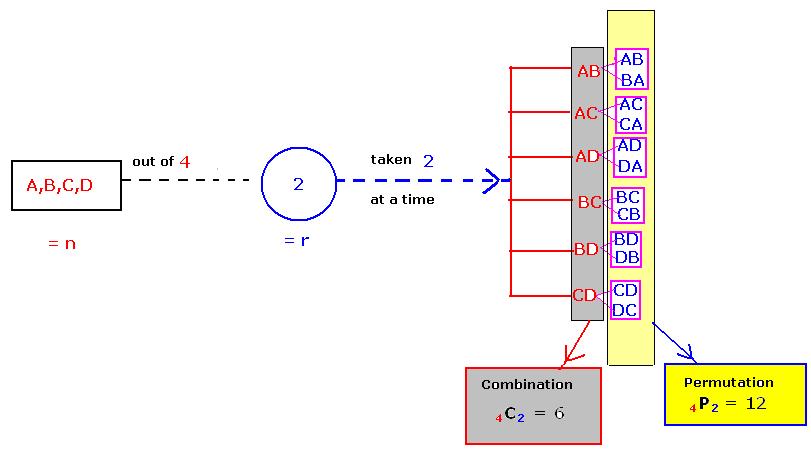
To find the formula for number of arrangements (Permutations)
possible among ‘n’ things with ‘r’ things taken at a time.
Method:
Let us assume that we have
‘n’ number of objects and ‘r’ number of boxes.
Let boxes be numbered as 1,2,3,….(r-1),r.
Our task is to fill these
boxes by taking ‘r’ objects at a time from ‘n’ number of objects.
|
Box No. |
1 |
2 |
3 |
…… |
(r-1) |
r |
|
No of
ways |
n |
(n-1) |
(n-2) |
|
n-(r-2) |
n-(r-1) |
1. First box can be filled in n different ways.
2. Second box can be filled
in (n-1) different ways.
3. Third box can be filled in
(n-2) different ways.
…
r. r’th
box can be filled in
(n-r+1) different ways.
By fundamental principle, r
boxes can be filled in
n*(n-1)*(n-2)*(n-3)…..(n-r+1)
ways
This is the number of
permutations of ‘n’ things taken ‘r’ at a time and is denoted by nPr
nPr =
n*(n-1)*(n-2)*(n-3)…..(n-r+1) =======è(1)
By substituting r=n in the
above equation we get
nPn
= n*(n-1)*(n-2)*(n-3)…..(n-n+1)
= n*(n-1)*(n-2)*(n-3)…..*1
nPn =n!
Let us multiply and divide
RHS of equation (1) by the same term (n-r)*(n-r-1)*…..3*2*1 we get
nPr
= {n*(n-1)*(n-2)*(n-3)…..(n-r+1)*
(n-r)*(n-r-1)*…..3*2*1}/{(n-r)*(n-r-1)*…..3*2*1}
=
{
n!= 1*2*3……*n and (n-r)! =
1*2*3….*(n-r)}
Since nPr= ,
Note:
nP1=
= 
= n
nP1
=n
nP(n-1)
=
(Substitute r = (n-1) in nPr)
= n! (1!= 1)
nP(n-1)=
n!= nPn
(n-r)!
= n!/ nPr{ nPr=
n!/(n-r)! }
By substituting r=n in the
above equation we get
0!
= n!/
nPn
= n!/n!
( nPn=
n! )
=1
0! =1
We summarise the following:
|
n = n!/(n-1)! |
|
nPn =n! |
|
nP1 =n |
|
nP(n-1)= n!= nPn |
|
0! =1 |
1.9.2 Problem 1 :
In how many ways the letters of the word COMPUTER can
be arranged? How many of these begin with M?
Solution:
Since the number of letters
in the word = 8, we can form 8!=40320 different words
of 8 letters.
|
Position
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Letters |
M |
Fill
from letters among C,O,P,U,T,E,R |
||||||
If M is fixed in the first
place then we are left with (n=7) letters to fill the other 7 places.
Then, the number of possibilities
are = 7! =5040 words
1.9.2 Problem 2:
How many 3 digit numbers can be formed using the digits2,3,4,5and
6 without repetitions? How many of these are even numbers?
Solution:
We know nPr
= : It is given that n=5(2,3,4,5,6)
and r=3
|
Hundred |
Ten |
Unit |
|
Choose
From (2,3,4,5,6) |
||
Number of 3 digit numbers which can be
formed = 5P3 = 
= 
=60
Among these, even numbers
are those ending with 2,4 and 6(unit place is 2 or 4 or
6)
Let us find out how many 3
digit numbers can be formed that ends with 2.
|
Hundred |
Ten |
Unit |
|
Choose
From (3,4,5,6) |
2 |
|
Even numbers:
Since the unit place is
already taken by 2,
we can only have 3, 4,5and 6 in hundredth and tenth places.
Since 2 will always be in
the units place, we only
need to find all the 2
digit numbers possible with 3,4,5 and 6(r=2).
The number of 2 digit
numbers that can be formed using (n=4) digits (3,4,5,6)
are =4P2= 
= 4*3 = 12
So with 2 in units place we
can have 12 3-digit numbers.
Similarly with 4 in units
place we can have 12 3-digit numbers.
Similarly with 6 in units
place we can have 12 3-digit numbers.
In all we can have 36(=12+12+12) even numbers.
1.9.2 Problem 3:
How many 3 digit numbers can be formed using 0,1,2,3?
Solution:
Here n=4 and r=3.
The number of 3 digit
numbers that can be formed are 4P3 =
= 4!=24
However, in case of 3 digit
numbers, a number starting with 0 can not be considered as a 3 digit number
(012 is not a 3 digit number but it is a 2 digit number).
Hence from the result we
need to subtract the number of 3-digit numbers starting with 0.
Let us find out the number
of 3-digit numbers starting with 0 .So we have n=3( 1,2,3)
and r=2
With 0 as the first digit,
number of 3-digit numbers we can make=3P2 = 3! =6.
Thus we can make 18(=24-6) 3-digit numbers from 0,1,2,3.
1.9.2 Problem 4:
In how many ways can 7 different books be arranged in a shelf? In how many ways
can we arrange three particular books so that they are always together?
Solution:
Here n=7. So the number of
ways these books can be arranged is 7! = 5040.
Let the books be A,B,C,D,E,F,G.
It is said that three books need to be together. Let they be B, C and D. For easy
understanding we can tie these 3 books together and call this bundle as H. So we are left with A,H,E,F,G(5
objects). These can be arranged in 5!=120 ways.
Since H is bundle of 3
books (B,C,D). The books in the bundle H themselves
can be arranged in 3!=6
ways.
Thus we have 6*120=720
ways of arranging 7 books such that 3 books are always together.
1.9.3
Combinations:
1.9.3 Example 1 :
Let A , B and C be students of your class. A photographer was asked to take
photos such that:
1. Different combinations
of 2 students in one snap shot
2. Different combinations
of 3 students in a snap shot
How many shots does he need
to take?
Working:
Example 1.1: Photo
session for group of 2 students
It can be seen from the
example 1.9.1.1.1 that,
the following arrangements are possible
|
I position |
A |
B |
C |
|||
|
II position |
B |
C |
A |
B |
C |
A |
But for a photo session we
notice that AB = BA, BC = CB, and CA=AC.
Though there are 6
arrangements possible, we only have 3 unique combinations (AB, BC, CA).
Example 1.2: Photo
session for group of 3 students
It can be seen from the
example 1.9.1.1.2 that, the following arrangements are possible
|
I position |
A |
B |
C |
|||
|
II position |
B |
C |
A |
B |
C |
A |
|
III position |
C |
B |
C |
C |
B |
C |
But for a photo session all
the 6 combinations are same.
Though there are 6 arrangements
possible, there is only one unique combination (ABC).
1.9.3 Example 2:
Let A B C D be 4 students in your class . A
photographer was asked to take photos such that:
1. Different combinations
of 2 students in one snap shot
2. Different combinations
of 3 students in one snap shot
How many snap shots does he
need to take?
Working:
Example 2.1: It can be
seen from the example 1.9.1.2.1 that, the following 12 arrangements are possible
|
I position |
A |
B |
C |
D |
||||||||
|
II position |
B |
C |
D |
A |
C |
D |
A |
B |
D |
A |
B |
C |
Notice that for a photo
session AB=BA, AC=CA, AD=DA, BC=CB, BD=DB and CD=DC.
Though 12 arrangements are possible , we only
have 6(=3*2) unique combinations (AB, AC, AD, BC, BD, CD).
Example 2.2: It can be
seen from the example 1.9.1.2.2 that, the following 24 arrangements
are possible
|
I position |
A |
B |
C |
D |
||||||||||||||||||||
|
II position |
B |
C |
D |
A |
C |
D |
A |
B |
D |
A |
B |
C |
||||||||||||
|
III position |
C |
D |
B |
D |
B |
C |
C |
D |
A |
D |
A |
C |
B |
D |
A |
D |
A |
B |
B |
C |
A |
C |
A |
B |
Note for a photo session
ABC=BAC=ACB=BCA=CAB=CBA
ABD=ADB=BAD=DAB=DBA=BDA
ACD=ADC=CAD=DAC=DCA=CDA
BCD=BDC=CBD=CDB=DBC=DCB
are
all same.
Though 24 combinations are
possible, there are only 4
unique combinations. (ABC, ABD, ACD, BCD)
The number of combinations
of ’n’ things taken ‘r’ things at a time is denoted by nCr
Let us analyse
our results
|
Examples |
Total Number of students(n) |
Number of students Per shot |
Number of combinations |
Notation |
|
Example
1.1 |
3 |
2 |
3 |
3C2 |
|
Example
1.2 |
3 |
3 |
1 |
3C3 |
|
Example
2.1 |
4 |
2 |
6 |
4C2 |
|
Example
2.2 |
4 |
3 |
4 |
4C3 |
Let us find the
relationship between permutations(1.9.1) and combinations(1.9.3) using
the examples 1 and 2 of Permutations and Combinations.
|
Examples |
Number of students(n) |
Number of students taken at a time(r) |
Number of Permutations nPr) (1.9.1) |
Number of Combinations(nCr) (1.9.3) |
nPr/nCr = |
|
Example
1.1 |
3 |
2 |
6= 3P2 |
3=3C2 |
2=2! |
|
Example
1.2 |
3 |
3 |
6= 3P3 |
1=3C3 |
6=3! |
|
Example
2.1 |
4 |
2 |
12= 4P2 |
6=4C2 |
2=2! |
|
Example
2.2 |
4 |
3 |
24= 4P3 |
4=4C3 |
6=3! |
We notice that nPr= nCr *
r! nCr =
nPr÷r!
Formula for number of combinations of ‘n’ things taken
‘r’ at a time:
In the example 2.1
discussed above we notice the following
(Permutations of ‘n’ things taken ‘r’ at a time)= (Selection (Combination) of ‘n’
things taken ‘r’ at a time)*(Arrangement of ‘r’ things)
nPr = nCr* rPr
1.9.3 Problem 1:
If nPr
= 336 and nCr=56 find n and r
Solution:
We know nPr÷nCr
= r!
r!= 
= 6=3*2*1=3!
r=3
Substitute r=3 in nCr= nPr÷r!
= {n! ÷ (n-r)} ÷r!
= {n*(n-1)*(n-2)*(n-3)! ÷
(n-3)! }÷3!
56 = n*(n-1)*(n-2) ÷6
I.e. 56*6 =336 =
n*(n-1)*(n-2) = 8*7*6
n=8
1.9.3 Problem 1:
A king has 8 different types of ornamental jars in his courtyard. Tell me the
number of different combinations in which theses can be arranged?
(Lilavati Shloka 116)
Solution:
Total number of jars(n) =8
|
No |
Type
of arrangement |
Nos |
|
1 |
No of
arrangements with 1 jar at a time |
8C1 |
|
2 |
No of arrangements with 2 jars at a time |
8C2 |
|
3 |
No of arrangements with 3 jars at a time |
8C3 |
|
4,5,6 |
------------------ |
|
|
7 |
No of arrangements with 7 jars at a time |
8C7 |
|
8 |
No of arrangements with 8 jars at a time |
8C8 |
Total number of
arrangements = 8C1+
8C2
+ . . . + 8C7
+ 8C8 =255 = 28-1
1.9.3 Problem 3 :
A Marriage bureau is in the business of identifying girls
for boys and boys for girls. They are having 5 girls and 4 boys in their
register looking for a match. In how many ways they can make proposals with 2
boys and 2 girls?
Solution:
1. There are 4 boys. The
number of ways in which 2 boys can be grouped are 4C2=4*3*2!/2!*2!=6
2. There are 5 girls. The
number of ways in which 2 girls can be grouped are 5C2=5*4*3!/3!*2! = 10
For every group of 2 boys
selected out of 6 groups, we can match with every group of 2 girls selected out
of 10 groups.
Total number of
proposals possible = 6*10=60
1.9.3 Problem 4 : A team has 10 players. Only
six can fit into one photo frame. Manager has to be in each of the photo
session. A photographer was asked to give an estimate for all the different
combinations of photos. A photo with frame costs Rs.22. Find out the estimate
given by photographer to the Manager
Solution:
Here n =10, r=5( manager has to be in every photo)
The number
of 5-member groups teams that can be formed from 10 members are
= 10C5
= 10!/5!*5!
= (10*9*8*7*6*5!)/(5!*5!)
= 10*9*8*7*6/120( 5! gets cancelled)
= 9*4*7 =252 photos
Total cost = 252*22= Rs.5, 544
1.9.3 Problem 5 :
Your school has one teacher for each of the subjects :
Mathematics, Social science, General Science, Moral science, English, Hindi,
Local Language, Physical Training. One of them is a headmaster.
(a) How many committees of
5 members can be formed?
(b) How many of them will
not have Headmaster in them?
Solution:
Number of teachers (n) = 8
Number of teachers in the
committee (r) =5
Number of committees
that can be formed is
= 8C5=
8!/(8-5)!*5!= 8*7*6*5!/3!*5!= 8*7*6/6 = 56
If we are to have Headmaster in the committee,
then we are left with only 7 teachers for selection. In such a case
The number of teachers (n)
= 7.
Since headmaster is already
a member of the committee, we only need to form a committee of 4 members (r) =4.
Number of committees
with head master is
= 7C4= 7!/(7-4)!*4!= 7*6*5*4!/3!*4!= 7*6*5/6 = 35
No of committees without
headmaster = total number of committees – Number of committees with head master
= 56-35 =21
1.9.3 Problem 6 :
There are 20 non collinear points on a plane. How many (a) straight lines (b)
triangles can be formed by joining these points?
Solution:
|
The
number of non collinear points (n=20) Since
straight line has 2 points (r=2), Total
number of straight lines that can be formed are = 20C2=
20!/(20-2)!*2!= 20*19*18!/18!*2! =
20*19/2 = 190 Since
triangles are formed with 3
points(r=3), Total
number of triangles that can be formed are = 20C3=
20!/(20-3)!*3!= 20*19*18*17!/17!*3! =
20*19*18/6 = 1140 |
|
Solution:
1.9.3 Problem 6 :
In a hexagon how many triangles can be formed?
Solution:
The number of vertices in a
hexagon (n)=6
The number of points
required for a triangle(r) =3
Number
of triangles that can be formed in a hexagon are
= 6C3=
6!/(6-3)!*3!= 6*5*4*3!/3!*3!= 20
1.9.3 Problem 7: A country had selected a
team of 8 batsmen and 7 bowlers to play a cricket match in
Solution:
If he chooses to have 5
bowlers then he can only have 6 batsmen out of 8.
If he chooses to have 6
bowlers then he can have 5 batsmen out of 8.
For every group of bowlers the
captain chooses, he has several choices of groups of batsmen and hence total
choice available for a particular option is product of these two choices.
|
Possibilities |
Total bowlers available =7 |
Total batsmen available =8 |
No of combinations |
|
|
1 |
5 (r=5) |
6 (r=6) |
=7C5*8C6 |
21*28=588 |
|
2 |
6 (r=6) |
5 (r=5) |
=7C6*8C5 |
7*
56=392 |
The captain has a choice of 980(588+392)
choices!!!
1.9.3 Problem 8: Indian
parliament has selected 8 members to form a 5-member Social Welfare Committee.
The Health Minister and Women Welfare Ministers are among these 8 members. The
committee’s role is to give recommendations for improvement of Welfare of
Citizens. There is a rule that the committee should be headed by a Minister and
there can not be more than one minister in the same committee. Find out how
many committees can be formed as per the rule?
Solution:
Since the committee has to
be headed by a minister, one of the ministers has to be in the committee. With
one minister being a member of committee and two ministers can not be in the
same committee,
Number of members available
for selection is (n=6)(=8-2)
Since one minister is
always in the committee, we need to select only 4 members for the committee
(r=4)(=5-1)
The no of ways
committee can be formed =6C4= 15
1.9
Summary of learning
|
Properties |
Permutations |
Combinations |
|
Meaning ====> |
Arrangement
of things in an orderly manner |
Selection
of different objects |
|
Example ====> |
How
many different words can be formed from the letters of the word ‘MATHS’ |
How
many 10 member hockey team be
formed from a list of 20 players |
|
Definition ====> |
No of ways
of arranging ‘n’ things taken ‘r’ things at a time |
No of
combinations of ‘n things taken ‘r’ things at a time |
|
Formula ====> |
nPr = n(n-1)(n-2)…(n-r+1)= |
nCr = nPr /r! |
|
Relationship ===> |
nPr= nCr * r! |
|