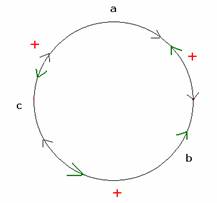
2.16 Cyclic Symmetry:

Observe the expression a+b+c --à(1) In the above expression, suppose we change a to b, b to c and c to a., what is the new expression? It is b+c+a -----à(2) Again, suppose we change b to c, c to a and a to b, what is the new expression? It is c+a+b ---à(3) We note that the expressions (1), (2) and (3) are all same.

Observe the expression a-b+c --à(1)

In the above expression, suppose we change a to b, b to c and c to a., what is the new expression?

It is b-c+a -----à(2)

Again, suppose we change b to c, c to a and a to b, what is the new expression?

It is c-a+b ---à(3)

We note that the expressions (1), (2) and (3) are not same unless a=b=c

An expression f(x,y,z) is said to be cyclic with respect to x,y,z if f(x,y,z) = f(y,z,x) = f(z,x,y)

You will again notice that the expressions x²+y²+ z² and x³+y³ +z³ are cyclic with respect to variables x, y, z

The expression a+b+c is symbolically represented by

Similarly the expression x³+y³ +z³ is symbolically represented by

2.16 Example 1: Write a²+b²+ c²-ab-bc-ca using notation

a²+b²+ c²-ab-bc-ca = (a²+b²+ c²)-(ab+bc+ca) = ( )or =()

2.16 Example 2:Expand

= xy(x²-y² )+yz(y²-z²)+zx(z²-x²)

2.16 Summary of learning

No	Points studied
1	Understanding of cyclic symmetry

Additional Points:

Factorisation of Cyclic expressions:

2.16 Problem 1: Factorise ab(a-b)+bc(b-c)+ca(c-a)

We use the following identities for factorisation

No	Formula/Identity	Expansion
1	(a+b)^2	a^2+b^2+2ab
2	(a-b)^2	a^2+b^2-2ab
3	(a+b)(a-b)	a^2-b^2
4	(a+b)^3	a^3+b^3+3ab(a+b)
5	(a-b)^3	a^3-b^3-3ab(a-b)
6	a^3+b^3	(a+b) (a^2 +b^2 -ab)
7	a^3-b^3	(a-b) (a^2 +b^2 +ab)

Solution:

ab(a-b)+bc(b-c)+ca(c-a) = a²b - ab²+bc(b-c)+ c²a - ca² (Expand first and last two terms)

= a²(b-c) - a(b²- c²) + bc(b-c) (Group those terms containing a² and a together)

= a²(b-c) - a(b+c)(b-c) + bc(b-c) (Factorise (b²- c²))

= (b-c)(a²-a(b+c)+bc) (Taking out (b-c) as common factor)

= (b-c)(a²-ab-ac+bc) (Group those terms containing a and c together)

= (b-c)(a(a-b)-c(a-b))

= (b-c)((a-b)(a-c)

= - (a-b)(b-c)(c-a)

If all the terms of an algebraic expression are of the same degree then such an expression is called a Homogenous expression.

Ex. a²+b²+2ab is a homogenous expression.

a²+b²+a is not a homogenous expression.