2.19 Quadratic Equations:

 

 

Do you find it interesting to solve the following problem taken from Lilavati (Shloka 71)?

 

In the epic battle of Mahabharata, Arjuna takes out certain number of arrows. He uses half of the arrows taken out to cut arrows of Karna, uses four times the square root of number of arrows to target horses of Karna. Uses 6 arrows to target Shalya, uses one each to target Chatra(Umbrella), flag and bow of Karna. Uses the remaining one to target Karna.Then tell me the number of arrows taken out by Arjuna.

 

Do you find it interesting to solve the following real life problem?

Problem  : Suppose you along with your friends had planned a picnic. You had budgeted Rs.480 for food. But at the last moment 8 of your friends did not go for the picnic. Because of their absence other members paid Rs.10 extra for food. Find out how much each one paid finally?

 

We have learnt to solve problems like:

1. Find the side of a square if its  perimeter is 60Meters.

Method:  Let  ’x’ be the side of a square, then perimeter = 4x

Thus 4x =60

 x =15 Meters

A linear equation has only one solution. The solution is called the root of the equation

 

2. If the area of a square is 25Sq.meters than what is its side?

Method: Let ‘x’ be the side of a square. Then area of the square = x2

Thus x2 = 25 =5*5

 x=5 Meters

Since 25 = -5*-5,  x= -5 also satisfies the condition x2 = 25. We can say that x = 5  are roots of the equation x2 = 25.

Because the side of a square can not be negative we do not consider x = -5 Meters as a solution to the problem.

Definition:  An equation involving a variable of degree 2 is called a ‘quadratic equation’

Note that x2 = 25 can also be  expressed as x2 - 25 =0.

Note that the above equation has a variable only in second degree and does not have variable in first degree (does not have terms like bx)

Definition: 

1.An equation of the type ax2 +c = 0 where a and c are real numbers   and a 0,  is called a ‘pure quadratic equation’  One example is  3x2 -16=0

 

2. An equation of the type ax2 +bx+ c = 0 where a, b and c are real numbers   and a 0 and b 0, is called a ‘Adfected  quadratic equation’  If b=0 then this equation becomes a  pure quadratic equation.

One example of an Adfected quadratic equation is 3x2 -5x-16=0

Note : If ab =0 then either a=0 or b=0 or both a =0 and b=0

 

Example : Let us solve 3x2 -16=0

 3x2 =16 (By transposition)

x2 =16/3

x = =     /=    (4/)

 

2.19 Problem 1 : Solve x2/2 – 3/4 = 29/4

 

Solution:

On transposition we have

x2/2 = 29/4+3/4 = (29+3)/4 = 32/4 =8

 x2 =16

 x = 4

 

2.19 Problem 2 : Solve (2m-5)2= 81

 

Solution:

(2m-5)2= 92

 2m-5 = 9

 2m = 9 +5 ( On transposition)

 2m = +9+5 =14 or 2m = -9+5 = -4

 m= 7 or m= -2

Verification:

When m =   7 : LHS=(2m-5)2=(9)2=81= RHS

When m = - 2:  LHS=(2m-5)2=(-4-5)2=(-4-5)2=(-9)2=81=RHS

 

2.19 Problem 3 : If  c2= a2+b2 Solve for b. If a=8 and c=17 find the value of b

 

Solution:

Given c2= a2+b2

 b2= c2-a2

 b = (c2-a2)

 Substituting given values for a and c in the above equation we get

b = (c2-a2)

   = (172-82)

   = (289-64) = (225) = 15

 

Verification:

When a=8 and b=15 we have RHS= a2+b2=64+225 =289 = 172= c2=LHS

 

2.19 Problem 4 : The volume of a cylinder of radius ‘r’ and height ’h’  is given by the formula Volume V = r2h 

1. Solve for r.

2. Find the radius of the cylinder if Volume =176 and height =14

 

Solution:

Assume  = 22/7

Since V =r2h 

r2= V/h

 r = (V/h)

It is given that V=176 and h = 14 

V/h = 176*7/(22*14)= 4

 r = 2

Since the radius can not be a negative number we conclude that r=2 units

 

Verification:

Given = 22/7, h =14 and arrived value for r=2:  RHS= r2h= 22*4*14/7 = 22*4*2=176=V= LHS

 

2.19.1 Solving Adfected Quadratic equations by Factorisation method

 

In This method we first express the quadratic equation as a product of 2 monomials and equate each of them to zero, and then find values of the unknowns. This method requires a lot of practice and can be mastered only over a period of time

 

2.19.1 Problem 1: Solve     6-p2=p

 

Solution:

This is equivalent to solving p2+p-6 = 0 ( By transposition)

We need to express LHS  in the form (x+a)(x+b) such that  a+b =1 and ab = -6. 

The factors of  - 6 are  (1, -6), (-1,6), (2,-3), (-2,3), (3,-2), (-3,2)

We note that only a = -2 and b= 3  satisfy the conditions a+b=1 and ab = -6

p2+p-6

= p2+3p-2p -6

= p(p+3) -2(p+3)  ---- take out the common factor (p+3)

= (p+3)(p-2)

Since p2+p-6 = 0

(p+3)(p-2) = 0 (if product of  two  terms is zero then one of the term has to be zero)

This is possible if p+3 = 0 or p-2 = 0

 p= -3 or p =2 are roots of the given equation

 

Verification:

Let us put p=2 in the given equation

LHS = 22+2-6 =4+2-6 = 0 =RHS. Similarly verify  for p = -3

 

2.19.1 Problem 2: Solve 6 y2+y -15 = 0.

 

Solution:

We need to express LHS in the form(ax+b)(cx+d)={ acx2 + x(ad+bc)+bd}such that ac=6, bd= -15 and  ad+bc =1

By inspection it can be seen that a=3, c=2,b=5,d= -3 satisfy the given conditions

6 y2+y -15

= 6 y2+10y -9y -15

= 2y(3y+5)-3(3y+5) – take out the common factor 3y+5

= (3y+5)(2y-3)

Since 6 y2+y -15 =0

(3y+5)(2y-3) =0

This is possible if 3y+5 = 0 or 2y-3 =0

  y = -5/3 or y =3/2 are roots of the given equation

 

Verification:

Let us put y=3/2 in the given equation

LHS = 6*9/4 +3/2 -15 =27/2+3/2 -15 = (27+3)/2 – 15 = 0 = RHS

Similarly verify for y= -5/3

 

2.19.1 Problem 3: Solve 13m = 6(m2+1)

 

Solution:

This is equivalent to 6m2-13m+6 =0

We need to express LHS in the form(ax+b)(cx+d)={ acx2 + x(ad+bc)+bd}such that ac=6, bd= 6 and  ad+bc = -13

By inspection it can be seen that that a=3, c=2,b=5,d= -3 satisfy the given conditions

6m2-13m+6=0

= 6m2-9m -4m+6

= 3m(2m -3) -2(2m-3)  ------à take out the common factor 2m-3

= (2m-3)(3m-2)

Since 6m2-13m+6 =0

(2m-3)(3m-2)=0

This is possible if 2m-3 = 0 or 3m-2 =0

 m = 3/2 or m =2/3 are roots of the given equation

 

Verification:

Let us put m=2/3 in the given equation

LHS= 6*4/9 -13*2/3 +6 = 8/3 -26/3+6 =(8-26)/3 +6 = 0 =RHS. Similarly try for m= 3/2

 

2.19.1 Problem 4: Solve y2-2y+2 =0

 

Solution:

We need to express this equation in the form(ax+b)(cx+d)={ acx2 + x(ad+bc)+bd}such that ac=1, bd= 2 and  ad+bc = -2

Since ac=1 and bd=2,   the possible values of a and c are:  a=1or c=1 and (b=2,d=1) or (b=1, d=2).

We also notice that with whatever combination of a, b, c, d, the condition ad+bc = -2 is not satisfied.

 

How do we solve such equations?

 

While solving problems 2.19.1.1,  2.19.1.2,  2.19.1.3 we noticed that it is not always easy to determine the factors.

 

Is it not logical to have a formula for finding roots of such equations?

We shall explain the method by an example

Example : Let us solve 2x2+3x+1 =0

 

No

Step

Explanation

1

x2 +(3/2)x+ (1/2) =0 

Divide both sides of the given equation by 2

2

x2+(3/2)x= -(1/2)

By transposing (1/2)  to RHS

If we can use the identity (x+a)2 = x2+2ax+ a2 we could find a solution to the given equation. If the equation in step 2  is compared with the above identity, we can say

2ax = (3/2)x and hence  a =3/4

3

x2+(3/2)x+ (3/4)2 = -(1/2)+ (3/4)2       

By adding (3/4)2 to both sides of equation in step 2

4

LHS of step 3= x2 +2(3/4)x + (3/4)2= [x+(3/4)]2

p2+2pq+q2 = (p+q)2 with p=x and q= 3/4

5

RHS of step 3= -(1/2)+ (3/4)2 =-(1/2)+ (9/16)= (1/16)

 

6

[x+(3/4)]2=(1/16)

Step 4 and 5

7

(x+(3/4)) = (1/4)

Square root of step 6

8

x = -(3/4) (1/4) = -(1/2) or -1

Simplification

 

 

We shall use the above method for solving generic equation ax2 +bx+ c =0

 

Formula for finding roots of the quadratic equation

 

Let us find the roots of the Quadratic equation whose general  form is ax2 +bx+ c =0, where a, b and c are real numbers and a 0 and b 0.

No

Step

Explanation

1

x2 +(bx/a)+ (c/a) =0 

Divide both sides by ‘a’

2

x2 +(bx/a) = -( c/a)

By transposing c/a  to RHS

3

x2 +(bx/a) + (b/2a)2 = -( c/a) + (b/2a)2      

By adding (b/2a)2 to both sides

4

LHS= x2 +(bx/a) + (b/2a)2= [x+(b/2a)]2

p2+2pq+q2 = (p+q)2 with p=x and q= b/2a

5

RHS = b2/4a2- c/a= (b2-4ac)/ 4a2

By having common denominator as 4a2

6

[x+(b/2a)]2 =(b2-4ac)/ 4a2

By Step 4 and 5 as LHS=RHS

7

x+(b/2a) =  ((b2-4ac)/ 4a2)

=  ((b2-4ac))/ 2a

Take square root of the last step

8

x = [-b  (b2-4ac)]/2a    

Transpose  b/2a to RHS

 

Therefore roots of the equation  ax2 +bx+ c =0  are:

x = [-b +(b2-4ac)]/2a  AND  x = [-b -(b2-4ac)]/2a    

Note : This  formula called quadratic formula was first given by the Indian mathematician Sridharacharya (1025AD)  The  formula is given in Lilavati also.(Shloka 67)

2.19.1 Problem 5: Solve 4x2+8x+4 = 0

 

Solution:

Here we have a =4, b=8, c =4

 b2-4ac = 64 – 4*4*4 = 0

 (b2-4ac) = (0) = 0

 

There fore as per the formula roots are

p = [-b +]/2a  =(-8+0)/8  = - 1      or

p = [-b -]/2a   = (-8-0)/8 =  - 1

 

Here the roots are same = - 1

 

Alternatively, note the given equation is equivalent to 4(x2+2x+1) = 4(x+1)(x+1) which again suggests that roots are -1.

 

2.19.1 Problem 6:  Solve    p2+p-6 = 0(Repetition of problem 2.19.1.1 solved earlier)

 

Solution:

This equation is of the form ax2 +bx+ c =0

Here we have a =1, b=1, c =-6

 b2-4ac = 1 – 4*1*(-6) = 25

  = (25) = 5

As per the formula, roots are

p = [-b +]/2a  =(-1+5)/2  = 2      or

p = [-b -]/2a   = (-1-5)/2 =  -3

These are the roots we got earlier

 

2.19.1 Problem 7:  Solve 6y2+y -15 = 0(Repetition of problem 2.19.1.2 solved earlier) and then factorise.

 

Solution:

This equation is of the form ax2 +bx+ c =0

Here we have a=6, b=1, c= -15

 b2-4ac = 1 – 4*6*(-15) = 361

 (b2-4ac) = (361) = 19

As per the formula, roots are

y = [-b +]/2a  =(-1+19)/12  = 18/12= 3/2     or

y = [-b -]/2a   = (-1-19)/12 =  -20/12 = -5/3

These are the roots we got earlier

Since 3/2 and -5/3 are roots of the given equation, (y-3/2)(y+5/3) are factors of the given equation

Note (y-3/2)(y+5/3) = (2y-3)(3y+5)/6

6y2+y -15 = (2y-3)(3y+5)

 

Exercise:  Solve example 2.19.1.3 using the formula method

 

2.19.1 Problem 8: Solve y2-2y+2 =0(Repetition of problem 2.19.1.4 which was not solved earlier)

 

Solution:

This equation is of the form ax2 +bx+ c =0

Here we have a=1, b=-2, c=2

 b2-4ac = 4 – 4*1*2 = -4

 (b2-4ac) = (-4) = 2

As per the formula, roots are

y = [-b +]/2a  =(2+2)/2  =  1+ or

y = [-b -]/2a   = (2-2)/2 =  1-

 

Because the root contained non real number we could not factorize in problem 2.19.1 Problem 4

 

Verification:

Let us put y= 1+ in the given equation

y2-2y+2 = (1+)2 -2(1+) +2 (Use the formula (a+b)2 =a2+b2+2ab to expand (1+)2)

= [1 +(-1) +2 ] +[-2 -2] +2

=  1-1 +2 -2 -2+2 = 0 = RHS.

Similarly you can verify for other root= 1-

 

2.19.1 Problem 9: Solve 2(3y-1)/(4y-3) = 5y/(y+2) -2

 

Solution:

RHS = [5y -2(y+2)]/(y+2) = (3y-4)/(y+2)

  We need to solve 2(3y-1)/(4y-3) = (3y-4)/(y+2)

On cross multiplication we get 2(3y-1)*(y+2) = (3y-4)*(4y-3)

i, e 2(3y2+6y –y -2) = 12y2-9y -16y+12

 6y2+10y -4 = 12y2-25y +12(By simplifying after transposing all terms from LHS to RHS we get:)

0 = 6y2-35y +16: 6y2-35y +16=0

This equation is of the form ax2 +bx+ c =0

Here we have a=6, b=-35, c= 16

 b2-4ac = 1225  – 4*6*16 = 1225-384  = 841

 (b2-4ac) = (841) = 29

As per the formula, roots are

y = [-b +]/2a  =(35+29)/12  =  16/3 or \

y = [-b -]/2a   = (35-29)/12 =  1/2

 

Verification:

Substituting these values in the equation  it can be seen  that LHS=RHS

 

2.19.1 Problem 10: Solve (y-1)(5y+6) /(y-3) = (y-4)(5y+6)/(y-2)

 

Solution:

On cross multiplication in the equation we get

(y-1)(5y+6)(y-2) = (y-4)(5y+6)(y-3) on expanding  terms on both LHS and RHS we get

LHS = (5 y2+6y-5y-6)(y-2)

= (5 y2+y-6)(y-2)

= 5 y3+ y2-6y -10 y2-2y+12

=5 y3 -9y2-8y+12

RHS

=  (5y2+6y-20y-24)(y-3)

= (5y2-14y -24)(y-3)

= 5y3-14 y2-24y  -15y2+42y+72

= 5y3-29y2+18y+72

Since it is given that LHS=RHS we have

5 y3 -9y2-8y+12= 5y3-29y2+18y+72. (On transposing all the terms from RHS to LHS we get:)

5 y3 -9y2-8y+12-(5y3-29y2+18y+72) =0(On simplification we get)

20y2-26y-60 = 0 ( By taking out 2 as a common factor)

10y2-13y-30 = 0

This equation is of the form ax2 +bx+ c =0

Here we have a=10, b=-13, c= -30

 b2-4ac = 169  – 4*10*(-30) = 169+1200  = 1369

 (b2-4ac) = (1369) = 37

As per the formula, roots are

y = [-b +]/2a  =(13+37)/20  =  50/20 = 5/2 or

y = [-b -]/2a   = (13-37)/20 = -24/20 =  -6/5

Verification:

Substituting these values in the equation  it can be seen  that LHS=RHS

 

Alternative method of solving this problem:

Since (5y+6) is common factor for both sides in the given equation, we have two alternatives:

(1). When 5y+6 = 0:

Then we have 5y= -6  I.e.  y = -6/5

  y = -6/5 is  a solution to the given problem  ---------à(1)

(2) When 5y+6  0 we can divide both sides of the given equation by 5y+6 then we get

[(y-1)/(y-3)] =[(y-4)/(y-2)] : By cross multiplication we get

                   (y-1)(y-2) = (y-4)(y-3)

i,e  y2-2y-y+2 = y2-3y-4y+12

i,e  y2-3y+2 = y2-7y+12: (On transposition we get)

i,e  y2-3y+2-( y2-7y+12)=0

i,e  y2-3y+2-y2+7y-12=0

i,e  4y-10=0

i,e  4y=10 or y=10/4 =5/2  ---------------------------à(2)

From (1) and (2) we conclude that 5/2 and -6/5 are roots of the given equation

 

2.19.1 Problem 11: Solve y/(y+1) + (y+1)/y = 25/12

 

Solution:

On simplifying LHS we get

[y*y +(y+1)(y+1)]/[y(y+1)]

= (y2+y2+2y+1)/( y2+y)

Since LHS = RHS we get

(y2+y2+2y+1)/( y2+y) = 25/12 (On cross multiplication we get)

12(y2+y2+2y+1) = 25( y2+y)

 24y2+24y+12 = 25y2+25y. On transposing LHS to RHS we get

0 = y2+y-12

This equation is of the form ax2 +bx+ c =0

Here we have a=1, b=1, c= -12

 b2-4ac = 1  – 4*1*(-12) = 1+48 = 49

  = (49) = 7As per the formula, roots are

y = [-b +)]/2a  =(-1+7)/2  =  3 or 

y = [-b -)]/2a   = (-1-7)/2 =  - 4

Verification:

Substituting these values in the equation it can be seen that LHS=RHS

 

2.19.1 Problem 12 : Solve (3x2-5x+2) (3x2-5x-2)=21

 

Solution:

1.  Let 3x2-5x = y then solve for y in (y+2) (y-2) =21

2.  Substituting value for y in the equation 3x2-5x = y solve for x.

Answer: x = - (-5)  (25+60)/2*3 = 5  (85)/6

 

2.19.1 Problem 13 (Problem given at the start of this section): Suppose you along with your friends had planned a picnic. You had budgeted Rs.480 for food. But at the last moment 8 of your friends did not go for the picnic. Because of their absence other members paid Rs.10 extra for food. Find out how much each one paid finally?

 

Solution:

Let ‘x’ be the number of people who were supposed to go to picnic.

Therefore the food bill per head = 480/x

Since 8 did not join finally only (x-8) people went for the picnic

 The revised food bill per head = 480/(x-8)

This is given to be Rs 10 more than what was planned earlier

 The new rate = old rate +10

So we have 480/(x-8) = 480/x + 10 

After simplifying RHS we get

480/(x-8) = (480+10x)/x. (On cross multiplication we get)

480x = (480+10x)(x-8) (On expanding RHS we get )

RHS= 480x -480*8 +10x*x-80x

 = 480x -  3840+ 10x2-80x = 10x2+400x-3840

0 =10x2+400x-3840-480x. (By  transposing 480x to RHS)

I.e. 0 =10x2-80x-3840. Dividing both the sides of this equation by 10 we get

x2-8x-384 =0

This equation is of the form ax2 +bx+ c =0

Here we have a=1, b= -8, c= -384

 b2-4ac = 64  – 4*1*(-384) = 64 +1536 =1600

   = (160000) = 40

As per the formula, roots are

x = [] =(8+40)/2  =  24 or

x = [-b -]/2a   = (8-40)/2 =  -16

 

Since number of people can not be negative, the correct solution is 24

Thus 24 friends   had planned to go out for a picnic

Therefore the revised food bill per head =()=30 Rs

Verification:

Since 24 people had planned to go out for a picnic. The cost of food per head which was planned, was = 480/24 = Rs.20

Since 8 did not go, only 16 went for picnic

Therefore the revised cost of food is 480/16 = Rs 30 which is Rs 10 more than what was planned. This result matches with what is given in the problem.

 

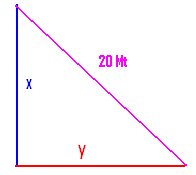
2.19.1 Problem 14:  Hypotenuse of a right angled triangle is 20mts. If the difference between lengths of other 2 sides is 4mts. Find the length of the sides

 

Solution:

If x and y are the sides of a Right angled triangle then by Pythagoras theorem we know that 

(Hypotenuse)2 = x2+ y2 .It is given that hypotenuse =20202 = x2+ y2      =======è (1)

Since we are given that x-y = 4: We have x= 4+y. Substituting this value of x in equation (1) and then expanding we have 400 = x2+ y2 =(4+y)2+ y2 = (16+8y+ y2)+ y2=16+8y+ 2y2 .

On transposing terms from LHS to RHS we have 0 = 2y2+8y-384.This equation is of the form ax2 +bx+ c =0

Here we have a=2, b= 8, c= -384  b2-4ac = 64  – 4*2*(-384) = 64+3072 =3136

  =(3136) = 56.As per the formula, roots are y = [-b +)]/2a  =(-8+56)/4  =  12 or

y = [-b -)]/2a   = (-8-56)/4 =  -16

Since the side of a triangle can not be a negative number, the correct answer for one side y =12mts and hence another side is16 mts(x=4+y)

 

Verification:

(side)2+ (side)2 = 122+ 162 = 144+ 256 = 400 =202 .Therefore hypotenuse=20 which is as given in the problem

 

2.19.1 Problem 15:  The distance between 2 cities is 1200km. A super fast train runs between these 2 cities. When the speed is increased by 30km/hr from its initial speed the journey time reduces by 2 hours. Find the initial speed of the train.

 

Solution:

Let x be the initial speed. Therefore time taken = 1200/x

If speed is increased by 30 km/hr then the revised time taken is 1200/(x+30).

It is given that the new time taken is 2 hours less than the original time

 1200/x-1200/(x+30) = 2

Exercise : Apply the formula to get the correct answer x=120

 

Verification:

1200/120 – 1200/150 = 10-8 =2 which is as given in the problem.

 

2.19.1 Problem 16: A sailor operates a motor boat between 2 ports which are 8 km apart. . He covers the journey (both ways) between 2 ports in 1hour 40minutes.If the speed of stream is 2km per hour. Find out the speed of boat in still water.

Note that, he has to sail the boat along with the stream in one way (reduces the journey time).On the return journey he has to sail the boat against the stream (The journey time increases)

 

Solution:

Let x be the speed of the boat.

We are given:

Total time taken to cover up and down = 1hr 40mins = 100/60 hour = 5/3 hours

Distance between port = 8km

The speed of stream is 2km/hr

Time taken to row down = 8/x+2 (Speed is the combined speed of stream and boat)

Time taken to row up = 8/x-2(Speed reduces by the speed of stream)

Total time taken = 8/(x-2) + 8/(x+2) which is given to be 5/3

Thus the equation to be solved is 8/(x-2) + 8/(x+2) = 5/3

 

Exercise: Apply the formula to get the correct answer x =10

 

Verification:

Total time taken = 8/(10-2) + 8/(10+2) = 8/8 + 8/12 = 1+2/3 = 5/3   which is the time given in the problem

 

2.19.1 Problem 17: A plane left 30 minutes later than the scheduled time. In order to reach the destination 1500 km away it has to increase the speed by 250km/hr from its regular speed. Find the regular speed and its normal journey time.

 

Solution:

Let x be the regular speed of the plane

The distance  to be covered is 1500km

 Normal journey time = distance/speed  = 1500/x

Since  the plane started late by half an hour,  the speed was increased to cover the distance  so that still it reached on time.

Thus the time available for the plane to cover is = (1500/x) -1/2

During this time it   still flew 1500 km with the speed of (x+250)

  distance = reduced journey time*new speed

I.e. 1500 = {(1500/x) -1/2}*(x+250) = (3000-2x)*(x+250)/2x

I.e. 3000x = (3000-x)(x+250) ( By cross multiplication)

I.e. 3000x = 3000x -x2+750000-250x

I.e. x2-750000+250x =0

 Apply the formula to get = 1750

 roots are :

x = [-b )]/2a    = (-250 1750)/2

Which gives x = 750 or x =-1000

Since the plane can not fly in a negative speed the solution has to be x = 750km/hr

 Normal journey time = 1500/750 = 2hr

 

Verification:

When the speed is increased by 250km/hr the new speed becomes 1000km/hr

 The time taken to cover 1500km = 1500/1000 = 1.5 Hours which is less than the normal flying hours by half an hour.

Since the plane left half an hour late, with the increased still it could reach on time. Hence our solution is correct.

 

2.19.1 Problem 18: O Girl, out of group of swans, 7/2 times the square root of the number are playing on the shore of a tank, the remaining two are fighting among themselves in the water. Find the total number of swans (Bhaskara 1114AD : ‘Leelavati :shloka’ 68)

 

Solution:

Let x be the total number of swans

The number of swans playing on the shore of tank = (7/2)

The number of swans fighting in water = 2

Thus we are required to solve the equation

 x= (7/2)+2

On solving we find the roots as 1/4 or 16

Since 1/4 is not feasible, the number of swans has to be 16

Verification:

Note 16 = 14+2 = (7/2) +2 which is as given in the problem and hence our solution is correct.

2.19.1 Problem 19: In the epic battle of Mahabharata, Arjuna takes out certain number of arrows. He uses half of the arrows taken out to cut arrows of Karna, uses four times the square root of number of arrows to target horses of Karna. Uses 6 arrows to target Shalya, uses one each to target Chatra(Umbrella), flag and bow of Karna. Uses the remaining one to target Karna.Then tell me the number of arrows taken out by Arjuna.(Lilavati Shloka 71)

 

Solution:

Let x be the total number of arrows.

 

No

Target

How many

1

Arrows of Karna

(x/2)

2

Horses of Karna

4

3

Shalya

6

4

Chatra, flag and bow of Karna

(1+1+1) =3

5

Karn(Remaining)

1

 

x = (x/2)+ 4 +6+3+1

 x –(x/2)-10 = 4

 (x/2)-10 = 4

 (x-20) = 8

 x2-40x+400 = 64x   --------à (a+b)2Formula).

 x2-104x+400 =0

 (x-100)*(x-4) =0

 x=100  Or   x=4

Number of arrows has to be more than 6 as Arjuna uses 6 to target Shalya. Hence the number of arrows used by Arjuna is 100

 

Verification:

100= 50+40+6+3+1

 

 

2.19.1 Problem 20: In a forest, square of 3 less than 1/5th  of the group of monkeys  went inside a cave. If the remaining one went up a tree, find the total number of monkeys in the group (Bhaskaracharya  : Bijaganita)

 

Solution:

Let x be the total number of  monkeys in the group. 

No

To  where?

How many

1

Cave

{(x/5)-3}2

2

Remaining

1

 

{(x/5)-3}2+1 =x

(x2/25) –(6x/5)+9+1=x

(x2/25) –(11x/5)+10=0

x2–55x+250=0

(x-50)*(x-5) =0

 x=50 Or x=5. It can not be 5, as (x/5)-3 can not be negative.

Verification:

50= (10-3)2+1= 49+1,

 

2.19.1 Problem 21: Solve 12( x2+ 1/ x2) -56(x+1/x) =  -89

 

Solution:

The given equation is 12( x2+ 1/ x2) -56(x+1/x) +89 =0

We know (x+1/x)2  = x2+ 1/ x2+2

 x2+ 1/ x2=(x+1/x)2 -2 

Substituting LHS value of the above equation in the given equation we get

12{(x+1/x)2 -2} -56(x+1/x) +89=0

I.e. 12(x+1/x)2 -24 -56(x+1/x) +89=0

I.e. 12(x+1/x)2  -56(x+1/x) +65=0

Let (x+1/x)= y

We are required to solve  12y2-56y+65 =0

By applying the formula we find that roots of this equation are y=5/2  or y=13/6

Case 1 :When y= 5/2: By substituting value of y we get

(x+1/x)= 5/2

I.e. (x2+1)/x = 5/2

I.e. 2(x2+1) = 5x

I.e. 2x2-5x+2 =0

By applying formula we get the roots of this equation as 2, 1/2

Case 2 :When y= 13/6: By substituting value of y we get

(x+1/x)= 13/6

I.e. (x2+1)/x = 13/6

I.e. 6(x2+1) = 13x

I.e. 6x2-13x+6 =0

By applying formula we get the roots of this equation as 2/3, 3/2

So the roots of the given equation are {2, 1/2, 2/3, 3/2}

 

2.19.2 Nature of roots of a Quadratic equation

 

Observations : Have  you observed the values of b2-4ac in  solving the problems?

 

In problem 2.19.1 .5, we have seen that b2-4ac = 0 and roots are same

In problem 2.19.1 .8, we have seen that b2-4ac <0 and roots are not real numbers

In all other examples we have seen that b2-4ac > 0 and roots are real numbers

 

The expression b2-4ac is called ‘discriminant’ and is denoted by (called delta)

 

We conclude the following:

 

Value of Discriminant(b2-4ac) =

Nature of roots=[-b ]/2a   

1

 = 0

Roots are real and equal

2

 >0 (Positive)

Roots are real and distinct(not equal)

3

 <0 (Negative)

Roots are imaginary(not real) and distinct

 

2.19.2 Problem 1: For what positive values of ‘m’, the roots of mk2-3k+1 =0 are equal, (real and distinct) and (imaginary and distinct)

 

 

Solution:

Here we have a=m, b= -3, c= 1

 b2-4ac = 9  – 4m

1. Roots are equal when  b2-4ac =0

(I.e. 9-4m =0, i.e. m = 9/4)

2. Roots are real and not equal when b2-4ac >0

(I.e. 9-4m >0, i.e. 9 >4m, i.e. m < 9/4)

3. Roots are imaginary and not equal when b2-4ac <0

(I.e. 9-4m <0, i.e. 9 <4m, i.e. m >  9/4)

 

2.19.2 Problem 2: For what values of ‘m’, the roots of r2-(m+1)r +4 =0 are equal, (real and distinct) and (imaginary and distinct)

 

Solution:

Here we have a=1, b= -(m+1), c= 4

 b2-4ac = (m+1) 2-16

= [(m+1)+4]*[(m+1)-4]  ===> By factorization

= (m+5)(m-3)

1. Roots are equal when  b2-4ac =0

(i.e. (m+5)= 0 or (m-3)=0 i.e. m=-5 or m=3

 

2. Roots are real and not equal when b2-4ac >0

(i.e. (m+5)(m-3) >0) (Note that when the product of 2 terms is +ve then both terms have to be +ve or both terms have to be –ve)

This is possible in two cases

Case 1:  both m+5 > 0 and m-3>0

I.e.         m> -5  and m>3: This is possible only if m>3

Case 2:  both m+5 < 0 and m-3 <0

I.e.         m< -5  and m<3: This is possible only if m <-5

 

3. Roots are imaginary and not equal when b2-4ac <0

(i.e. (m+5)(m-3) <0) (Note that when the product of 2 terms is -ve then one of the term is +ve and other term is -ve)

This is possible in two cases

Case 1: m+5 <0 and m-3>0

I.e.         m< -5 and m>3: This is not possible at all

Case 2:   m+5 > 0 and m-3 <0

I.e.         m> -5 and m<3: That is when value of m is between -5 and 3

The above findings can be represented on number line as follows.

 

 

 

2.19.2 Problem 3:  Find value of ‘p’ for which (p+1) n2+2(p+3)n +(p+8) =0 has equal roots

 

Solution:

This equation is of the form ax2 +bx+ c =0

Here we have a=(p+1), b= 2p+6, c= p+8

 b2-4ac = (2p+6)2  – 4*(p+1)(p+8) =  (4p2+24p+36) -4(p2+8p+p+8)= 4p2+24p+36 -4p2-36p-32 =-12p+4

If the roots are to be equal then b2-4ac =0

I.e.   -12p+4 = 0

I.e. p=1/3

As per the formula, roots for  p=1/3  are

n = [-b ]/2a  =[-2(p+3)0) ]/2(p+1)  =  - (p+3)/(p+1)

           = - (10/3)/(4/3) = -5/2

Verification:

Substituting n = -5/2 in the equation we get

(p+1) n2+2(p+3)n +(p+8)

= 25(p+1)/4 -5(p+3) +(p+8)

= 25(p+1)/4  -4p -7 ( By having 4 as common denominator, we get)

= (25p+25-16p-28)/4

= (9p-3)/4 (By substituting p = 1/3 we get

=0/4 = 0 = RHS of the given equation

 

2.19.2 Problem 4: Find value of ‘p’ for which (3p+1) c2+2(p+1)c +p =0 has equal roots

 

Solution:

This equation is of the form ax2 +bx+ c =0

Here we have a=(3p+1), b= 2p+2, c= p

 b2-4ac = (2p+2)2  – 4*(3p+1)p =  (4p2+4+8p) -4(3p2+p)= 4p2+4+8p -12p2-4p = -8p2+4p+4 = - 4(2p2-p-1)

If the roots are to be equal then b2-4ac =0

I.e.   2p2-p-1 = 0

LHS = 2p2-2p+p-1 = 2p(p-1)+(p-1) = (p-1)(2p+1)

Since 2p2-p-1 = 0 we have

(p-1)(2p+1) = 0

  p=1 or p= -1/2  are the answers

NOTE: To find roots of 2p2-p-1 = 0 we used factorisation method.

As per the formula, roots with p=1 is

c = [-b +]/2a  =[-2p-2 0) ]/2(3p+1)  =  - 4/8 =  -1/2

With p = -1/2 we get another value for c

NOTE: In the above problem we could use the formula twice to work out the example.

 

Verification:

 Substituting  c = -1/2 in the equation we get

(3p+1) c2+2(p+1)c +p

= (3p+1)/4+2(p+1)(-1/2) +p

=(3p+1)/4 –(p+1) +p

=(3p+1)/4 -1 (By having 4 as common denominator we get)

= [(3p+1) -4]/4 (By substituting p =1 we get

= 0/4 = 0=RHS of given equation

Exercise : Verify that p = -1/2   gives equal roots for (3p+1) c2+2(p+1)c +p =0

 

2.19.2 Problem 5: Find value of ‘p’ for which 2y2-py +1 =0 has equal roots

 

Solution:

This equation is of the form ax2 +bx+ c =0

Here we have a=2, b= -p, c= 1

 b2-4ac = p2 -8

If the roots are to be equal then b2-4ac =0

I.e.   p2 = 8 :

I.e. p =  2

Exercise: Verify that this value of p gives equal roots to the given equation

 

2.19.3 Relationship between roots and co-efficients:

 

Let ‘m’  and ‘n’ be the roots of quadratic equation of the form ax2 +bx+ c =0

 (x-m)(x-n) = 0

We also have seen that the roots of this equation are

x = [-b +]/2a  CxÀªÁ x = [-b -]/2a   

 m = [-b +]/2a

    n  = [-b -]/2a

 m+n = [-b +]/2a + [-b -]/2a

= -2b/2a = -b/a

mn = [-b +]/2a * [-b -]/2a (By applying formula for (a+b)(a-b) we get

= [ (-b)2- {}2] /4a2

= [b2 -(b2-4ac) ] /4a2

= 4ac/4a2

= c/a

We conclude:

1) Sum of the roots of a quadratic equation = -b/a

2) The product of roots of a quadratic equation = c/a

 

2.19.3 Problem 1: Find the sum and product of roots of x2 +(ab)x+ (a+b) =0

 

Solution:

This equation is of the form ax2 +bx+ c =0

Here we have a=1, b= ab, c= (a+b)

m+n = -b/a = -ab/1 =  -ab

 mn =c/a =(a+b)/1 = (a+b)

 

2.19.3 Problem 2 Find the sum and product of roots of pr2 = r-5

 

Solution:

This is equivalent to pr2 –r+5= 0

This equation is of the form a x2 +bx+ c =0

Here we have a=p, b= -1, c= 5

m+n = -b/a = 1/p 

mn =c/a = 5/p

2.19.4 Formation of equation with given roots

 

If ‘m’ and ‘n’ be the roots of the quadratic equation ax2 +bx+ c =0

Then we know (x-m)(x-n) = 0

But (x-m)(x-n)

=x(x-n)-m(x-n)

= x2 –xn –mx +mn

= x2 –x(n+m) +mn

= x2 –(n+m)x +mn

The general format is

 x2 –(sum of roots)x +(product of roots) =0

 

2.19.4 Problem 1: If ‘p’ and ‘q’ are the roots of the equation 2a2-4a+1=0 find the value of  (p+q)2+4pq and p3 +q3 and also form the equation whose roots are p3 and q3

 

Solution:

This equation is of the form ax2+bx+ c =0

Here we have a=2, b= -4, c= 1

p+q = -b/a = 4/2 =2  

    pq =c/a =1/2

 (p+q)2+4pq=4+2 =6

We know the general formula for a3+b3= (a+b) (a2+b2-ab)

p3 +q3 

= (p+q)( p2+q2-pq)

= (p+q)[( p2+q2+2pq) -3pq)]

= (p+q)[( p+q)2-3pq]

=2*[4-3/2] =5 (By substituting vales for (p+q) and pq )

We are also required to form an equation whose roots are p3 and q3 

Sum of roots = p3 +q3  =5( we had just calculated above)

Product of roots = p3*q3  = (pq)3 =(1/2)3 =1/8

 The desired equation is 

x2-(sum of roots)x+ (product of roots)= 0

I.e. x2-5x+ 1/8= 0 (by multiplying terms by 8 we get)

I.e.  8x2-40x+1=0

 

2.19.4 Problem 2:  Form a quadratic equation whose roots are p/q and q/p

 

Solution:

We are given m =p/q, n=q/p

m+n = p/q+q/p = (p2+q2)/pq:

    mn = p/q*q/p =1

The standard form is x2 –(n+m)x +mn= 0

I.e. x2 –(p2+q2)x/pq +1 = 0

I.e. (pqx2 –(p2+q2)x +pq)/pq =0( Have pq as common denominator)

I.e. pqx2 –(p2+q2)x +pq=0

2.19.4 Problem 3: If one root of the equation x2+px+q=0    is 3 times the other prove that 3p2=16q

 

Solution:

This equation is of the form ax2+bx+ c =0

Here we have a=1,b=p,c=q

Let m and n be the roots of the equation.

m+n = -b/a = - p and   mn=c/a = q

It is given that one of the root is 3 times another. So let m =3n

 p = - (m+n) =-(3n+n)= -4n   and q =mn=3n*n = 3n2

 3p2= 3(-4n)2= 48 n2=16*3n2 = 16q(3n2=q)

 

2.19.4 Problem 4: Find the value of ‘p’ so that the equation 4x2-8px+9=0   has roots whose difference is 4

 

Solution:

This equation is of the form ax2+bx+ c =0

Here we have a=4,b=-8p,c=9

Let m and n be the roots of the equation

1) m+n = -b/a = 8p/4=2p  ===è(1)

2)  mn= c/a = 9/4              ===è(2)

Since the difference between roots is 4 let n=m+4 Substituting this value in (1)  we get

m+n = m+m+4 = 2p: i,e 2m= 2p-4: i,e m=p-2 ------à(3)

By substituting   n= m+4 in (2) we get

m(m+4) =9/4

I.e. m2+4m - 9/4 =0

I.e. (p-2)2+4(p-2) - 9/4 =0(m=p-2 as per (3))

I.e. p2-4p+4 +4(p-2) - 9/4 =0 (By expanding (p-2)2 using formula )

I.e. p2-4p+4 +4p-8 - 9/4 =0

I.e. p2-4 - 9/4 =0

I.e. p2-25/4 =0

I.e. p2= 25/4

p =  5/2

 

Verification: Substitute value of p (-5/2) in the given equation we get

4x2-8px+9=0  

i.e. 4x2-8*(-5/2)x+9=0 

i.e. 4x2+20x+9=0   This is of the form ax2+bx+c=0   where a=4, b=20, c=9

 b2-4ac = 400  – 4*4*9 = 400-144 =256

  = (256) = 16

As per the formula, roots are

x = [-b +]/2a  =(-20+16)/8  =   -4/8

x = [-b -]/2a   = (-20-16)/8 =  -36/8

Notice that the difference between these two roots are 32/8 =4 which is as given in the problem

 

Exercise : Verify that p=5/2 also gives the same result

 

2.19 Summary of learning

 

 

No

Points to remember

1

The roots of quadratic equation ax2 +bx+ c = 0 are x = [-b+]/2a  AND   

[-b-]/2a  

2

If m and n are roots of a quadratic equation then the sum of the roots (m+n) = -b/a

3

If m and n are roots of a quadratic equation then the product of roots (mn) = c/a

4

If m and n are roots of a quadratic equation then the equation is x2 –(n+m)x +mn =0

 

 

2.19 Additional Points:

 

2.19.4 Binomial theorem:

We have learnt that any algebraic expression with 2 variables is called a binomial. We also know that

(x+y)0=1

(x+y)1=x+y

(x+y)2=x2+2xy+y2

(x+y)3= x3+3x2y+3xy2+y3

Similarly

(x+y)4= x4+4x3y+6x2y2+4xy3+y4

What are the observations?

 

1. The exponent of the first term(x) starts with the exponent of the binomial (n) and in subsequent terms it decreases by 1 till it is 0.

2. The exponent of the second term(y) starts with 0 and in subsequent terms it increases by 1 till it becomes equal to the exponent of the  

    binomial.

3. The sum of exponents of x and y in each term is equal to the exponent of the binomial.

4. There co-efficients of first and last term is always 1.

4. There is also a pattern among co-efficients of other terms as shown below.

 

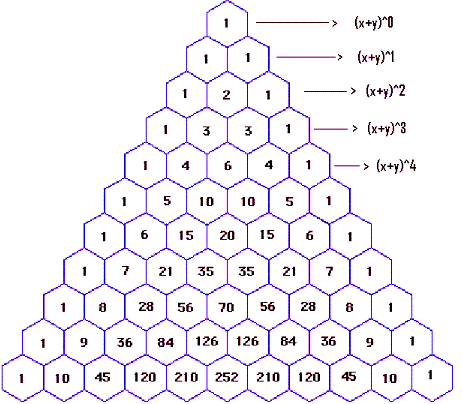
The above triangle has come to be known as Pascal Triangle named after Pascal (16th Century AD). However this arrangement called as ‘Meru Prastara’ was known to Indian Mathematicians much earlier and was first provided by Pingala (3rd century BC).

 

Since this method of finding co-efficients for large values of n is difficult, we have the following theorem called the Binomial theorem.

 

(x+y)n = nC0xn+ nC1xn-1y+ nC2xn-2y2+………+ nCrxn-ryr+……..+nCnyn

 

Where the co-efficient nCr  is defined as nCr= n!/[(n-r)!r!)] (Refer to section 1.9)

 

 

2.19.4 Problem 1: Find the 4th term of [3a+(1/2a)]7

 

By binomial theorem the 4th term is T4 = 7C3 x7-3y3= 7!/[4!3!)](3a)7-3(1/2a)3

=(7*6*5*4!)/ [4!3!)]34a4/(23a3)

= (35*81*a)/8

= (2835a/8)