2.19 ªÀUÀð ¸À«ÄÃPÀgÀtUÀ¼ÀÄ(Quadratic Equations):
CdÄð£À£ÀÄ ªÀĺÁ¨sÁgÀvÀ
AiÀÄÄzÀÞzÀ°è PÀtð£À£ÀÄß PÉÆ®è®Ä §vÀÛ½PÉ ¬ÄAzÀ ºÀ®ªÀÅ ¨ÁtUÀ¼À£ÀÄß
vÉUÉAiÀÄÄvÁÛ£É. vÉUÉzÀ ¨ÁtUÀ¼À°è CzsÀðzÀµÀÖjAzÀ PÀtð£À ¨ÁtUÀ¼À£ÀÄß
vÀÄAqÀj¸ÀÄvÁÛ£É. vÉUÉzÀ ¨ÁtUÀ¼À ªÀUÀðªÀÄÆ®zÀ 4 gÀµÀÖjAzÀ PÀtð£À PÀÄzÀÄgÉUÀ¼À£ÀÄß, 6 ¨ÁtUÀ½AzÀ ±À®å£À£ÀÄß, MAzÉÆAzÀjAzÀ PÀtð£À gÀxÀzÀ PÉÆqÉ, PÀtð£À gÀxÀzÀ
¨ÁªÀÅl, ªÀÄvÀÄÛ PÀtð£À ©®è£ÀÄß vÀÄAqÀj¸ÀÄvÁÛ£É. G½zÀ MAzÀÄ ¨Át¢AzÀ PÀtð£À£ÀÄß
PÉÆAzÀgÉ, §vÀÛ½PÉ ¬ÄAzÀ MlÄÖ JµÀÄÖ ¨ÁtUÀ¼À£ÀÄß vÉUÉAiÀÄÄvÁÛ£É? (°Ã¯ÁªÀw: ±ÉÆèÃPÀ 71)
ªÉÄð£À ¸ÀªÀĸÉå
©r¸ÀĪÀ D¸É EzÉAiÉÄÃ?
¤d fêÀ£ÀzÀ°è JzÀÄj¸ÀĪÀ PɼÀV£À ¸ÀªÀĸÉåUÉ GvÀÛgÀ UÉÆvÉÛÃ?
¸ÀªÀĸÉå: ¤ÃªÀÅ, ¤ªÀÄä ¸ÉßûvÀgÀÄ MnÖUÉ
MAzÀÄ ¥ÀæªÁ¸ÀPÉÌ ºÉÆÃUÀ®Ä §AiÀĸÀÄwÛÃj. DºÁgÀPÁÌV MlÄÖ 480gÀÆ. RZÁðUÀÄvÀÛzÉAzÀÄ ¯ÉPÀÌ
ºÁQ¢j. DzÀgÉ PÉÆ£ÉAiÀÄ PÀëtzÀ°è 8 ªÀÄA¢ ¤ªÀÄä ¸ÉßûvÀgÀÄ ¥ÀæªÁ¸ÀPÉÌ ºÉÆÃUÀ°®è.
EªÀgÀÄ ¨ÁgÀ¢zÀÄÝzÀjAzÀ, ¥ÀæwAiÉƧâgÀÆ DºÁgÀPÁÌV 10gÀÆ. ºÉaÑUÉ PÉÆqÀ¨ÉÃPÁ¬ÄvÀÄ.
ºÁUÁzÀgÉ ¥ÀæwAiÉƧâgÀÆ PÉÆ£ÉUÉ PÉÆlÖ ºÀt JµÀÄÖ?
£ÁªÀÅ FUÁUÀ¯Éà PɼÀV£À PÉ®ªÀÅ
¸ÀªÀĸÉå ©r¸ÀĪÀÅzÀ£ÀÄß PÀ°wzÉÝêÉ:
1. MAzÀÄ ªÀUÀðzÀ ¸ÀÄvÀÛ¼ÀvÉ 60«ÄÃlgï DzÀgÉ
CzÀgÀ §¢AiÀÄ GzÀÝ JµÀÄÖ?
PÀæªÀÄ: ªÀUÀðzÀ MAzÀÄ §¢: ‘x’ DVgÀ°. DUÀ
¸ÀÄvÀÛ¼ÀvÉ = 4x
4x =60
x =15 «ÄÃlgïUÀ¼ÀÄ
F jÃw gÉÃSÁvÀäPÀ
¸À«ÄÃPÀgÀtPÉÌ MAzÉà ¥ÀjºÁgÀ«gÀÄvÀÛzÉ. F ¥ÀjºÁgÀªÀ£ÀÄß ¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®
J£ÀÄßvÉÛêÉ. E°è 15, 4x = 60 J£ÀÄߪÀ ¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®.
2. MAzÀÄ ªÀUÀðzÀ «¹ÛÃtð 25 ZÀzÀgÀ
«ÄÃlgïUÀ¼ÁzÀgÉ CzÀgÀ MAzÀÄ §¢AiÀÄ GzÀÝ JµÀÄÖ?
PÀæªÀÄ: ªÀUÀðzÀ MAzÀÄ §¢AiÀÄ
GzÀÝ ‘x’ DVgÀ°. DUÀ D ªÀUÀðzÀ «¹ÛÃtð = x2
x2 = 25 =5*5
x=5 «ÄÃlgïUÀ¼ÀÄ
DzÀgÉ 25 = -5*-5 JAzÀÆ
DUÀÄvÀÛzÉ. x= -5 F
¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®ªÀÇ DVzÀÄÝ x2 = 25£ÀÄß vÀÈ¦Û ¥Àr¸ÀÄvÀÛzÉ. DzÀÝjAzÀ x
= 
5 F ¸À«ÄÃPÀgÀtzÀ
ªÀÄÆ®UÀ¼ÀÄ.
ªÀUÀðzÀ ¨ÁºÀÄ«£À GzÀÝ IÄt
¸ÀASÉåAiÀiÁUÀ®Ä ¸ÁzsÀå«®èªÁzÀÝjAzÀ x = -5 £Àß ¸À«ÄÃPÀgÀtzÀ ¥ÀjºÁgÀªÁV
vÉUÉzÀÄPÉƼÀÄîªÀÅ¢®è.
ªÁåSÉå: DªÀåPÀÛ
¥ÀzÀzÀ WÁvÀ 2 DVgÀĪÀ ¸À«ÄÃPÀgÀtªÀ£ÀÄß ªÀUÀð ¸À«ÄÃPÀgÀt (quadratic equation) J£ÀÄßvÉÛêÉ.
x2 = 25 EzÀ£ÀÄß x2
- 25 =0 JAzÀÆ §gÉAiÀĺÀÄzÀÄ (KPÉ ªÀÄvÀÄÛ ºÉÃUÉ ?)
F ¸À«ÄÃPÀgÀtzÀ°è ZÀgÁPÀëgÀ x £À WÁvÀ 2 ªÀiÁvÀæ«zÉ.
ªÉÆzÀ® WÁvÀzÀ ZÀgÁPÀëgÀ«®è.(bx JA§ CA±À«®è.)
ªÁåSÉå:
1. ax2
+c = 0 ¸À«ÄÃPÀgÀtzÀ gÀÆ¥ÀzÀ°è ªÀåPÀÛ¥Àr¸À§ºÀÄzÁzÀ ¸À«ÄÃPÀgÀtªÀ£ÀÄß ±ÀÄzÀÞ ªÀUÀð
¸À«ÄÃPÀgÀt (pure quadratic equation)J£ÀÄߪÀgÀÄ. a ªÀÄvÀÄÛ c UÀ¼ÀÄ
ªÁ¸ÀÛªÀ ¸ÀASÉåUÀ¼ÁVzÀÄÝ, a 
0 DVgÀÄvÀÛzÉ.
2. a, b ªÀÄvÀÄÛ c UÀ¼ÀÄ
ªÁ¸ÀÛªÀ ¸ÀASÉåUÀ¼ÁVzÀÄÝ a 0, b 0, DVgÀĪÀ ax2
+bx+ c = 0 gÀÆ¥ÀzÀ°è ªÀåPÀÛ¥Àr¸À§ºÀÄzÁzÀ ¸À«ÄÃPÀgÀtªÀ£ÀÄß «Ä±ÀæªÀUÀð ¸À«ÄÃPÀgÀt (Adfected quadratic
equation) J£ÀÄߪÀgÀÄ. E°è b=0 DzÀgÉ, CzÀÄ
±ÀÄzÀÞ ªÀUÀð ¸À«ÄÃPÀgÀtªÁUÀÄvÀÛzÉ.
«Ä±ÀæªÀUÀð ¸À«ÄÃPÀgÀtPÉÌ
GzÁºÀgÀuÉ: 3x2 -5x-16=0
GzÁºÀgÀuÉ: 3x2
-16=0 F ¸À«ÄÃPÀgÀtªÀ£ÀÄß ©r¸ÀĪÁ.
3x2 =16 (16 £Àß
§®¨sÁUÀPÉÌ vÀA¢zÉ, CxÀªÁ JgÀqÀÆ PÀqÉ 16 £ÀÄß PÀÆr¹zÉ)
x2 =16/3
x = 
= 
/
= (4/)
2.19 ¸ÀªÀĸÉå1: ©r¹: x2/2 – 3/4 = 29/4
¥ÀjºÁgÀ:
¥ÀPÁëAvÀgÀ
ªÀiÁrzÁUÀ,
x2/2 = 29/4+3/4 = (29+3)/4 = 32/4 =8
x2 =16
x
= 4
2.19 ¸ÀªÀĸÉå 2 : ©r¹: (2m-5)2=
81
¥ÀjºÁgÀ:
(2m-5)2=
92
2m-5 = 9
2m = 9 +5 (¥ÀPÁëAvÀgÀ
ªÀiÁrzÁUÀ)
2m = +9+5 =14 CxÀªÁ 2m = -9+5 = -4
m=
7 CxÀªÁ m= -2
vÁ¼É:
m = 7: DzÁUÀ, (2m-5)2=(9)2=81=
§®§¢.
m = - 2: DzÁUÀ, (2m-5)2=(-4-5)2=(-4-5)2=(-9)2=81= §®§¢.
2.19 ¸ÀªÀĸÉå 3 : c2= a2+b2 DVzÀÄÝ a=8, c=17 DzÁUÀ bAiÀÄ ¨É¯É K£ÀÄ?
¥ÀjºÁgÀ:
c2=
a2+b2
b2= c2-a2
b = 
(c2-a2) (DAzÀgÉ
ªÀUÀðªÀÄÆ®)
a ªÀÄvÀÄÛ c UÀ¼À ¨É¯ÉUÀ¼À£ÀÄß E°è
DzÉò¹zÁUÀ,
b = (c2-a2)
= (172-82)
= (289-64)
= (225)
= 15
vÁ¼É:
a=8, b=15 DzÁUÀ §®§¢= a2+b2=64+225
=289 = 172= c2=JqÀ§¢
2.19 ¸ÀªÀĸÉå 4 : MAzÀÄ
¹°AqÀj£À wædå ‘r’ JvÀÛgÀ ’h’ DzÁUÀ CzÀgÀ WÀ£À¥sÀ®(UÁvÀæ) = V = 
r2h
1. r£À ¸ÀÆvÀæ K£ÀÄ?
2. UÁvÀæ=176 , JvÀÛgÀ=14DzÁUÀ
¹°AqÀj£À wædå PÀAqÀÄ»r.
¥ÀjºÁgÀ:
V =r2h
r2= V/h
r = (V/h)
zÀvÁÛA±À: V=176, h =
14
= 22/7 (¸À«ÄÃ¥ÀzÀ ¨É¯É)
r2=V/h =
176*7/(22*14)= 4
r = 2
wædåªÀÅ IÄt
¸ÀASÉåAiÀiÁUÀĪÀÅ¢®è. DzÀÝjAzÀ r=2 ªÀiÁ£ÀUÀ¼ÀÄ.
vÁ¼É:
= 22/7, h =14, r=2:
§®¨sÁUÀ= r2h=
22*4*14/7 = 22*4*2=176=V= JqÀ¨sÁUÀ
2.19.1 «Ä±Àæ ªÀUÀð
¸À«ÄÃPÀgÀtªÀ£ÀÄß C¥ÀªÀvÀð£À PÀæªÀÄ¢AzÀ ©r¸ÀĪÀÅzÀÄ(Solving Adfected Quadratic equations by Factorisation method)
F «zsÁ£ÀzÀ°è £ÁªÀÅ ªÀUÀð
¸À«ÄÃPÀgÀtªÀ£ÀÄß JgÀqÀÄ ¢é¥ÀzÀUÀ¼À UÀÄt®§ÞªÁV §gÉzÀÄ, ¥ÀæwAiÉÆAzÀ£ÀÄß ¸ÉÆ£ÉßUÉ
ºÉÆð¹, ZÀgÁPÀëgÀzÀ ¨É¯ÉAiÀÄ£ÀÄß PÀAqÀÄ»rAiÀÄÄvÉÛêÉ. F «zsÁ£ÀPÉÌ vÀÄA¨Á
C¨sÁå¸À¨ÉÃPÀÄ ªÀÄvÀÄÛ ¸ÀjAiÀiÁV
PÀ°AiÀÄ®Ä vÀÄA¨Á ¸ÀªÀÄAiÀĨÉÃPÀÄ.
2.19.1 ¸ÀªÀĸÉå 1: ©r¹: 6-p2=p
¥ÀjºÁgÀ:
¥ÀPÁëAvÀgÀ ªÀiÁrzÁUÀ, zÀvÀÛ
¸ÀªÀĸÉå: p2+p-6 = 0
FUÀ, JqÀ¨sÁUÀªÀ£ÀÄß (x+a)(x+b) gÀÆ¥ÀzÀ°è
§gÉAiÀĨÉÃPÀÄ.
E°è a+b =1, ab = -6.
- 6 gÀ C¥ÀªÀvÀð£ÀUÀ¼À
AiÀÄÄUÀäUÀ¼ÀÄ (1, -6), (-1,6), (2,-3), (-2,3), (3,-2), (-3,2)
EªÀÅUÀ¼À°è a+b =1, ab =
-6. F ¤AiÀĪÀÄPÉÌ C£ÀĸÁgÀªÁVgÀĪÀ
UÀÄA¥ÀÅ
a = -2 and b= 3
p2+p-6
= p2+3p-2p -6
= p(p+3) -2(p+3)
---- ¸ÁªÀiÁ£Àå ¥ÀzÀ(p+3)ªÀ£ÀÄß ºÉÆgÀ vÉUÉzÁUÀ
= (p+3)(p-2)
p2+p-6 = 0
(p+3)(p-2) = 0 (JgÀqÀÄ ¥ÀzÀUÀ¼À UÀÄt®§Þ 0 DzÀgÉ
CªÀÅUÀ¼À°è MAzÀÄ ¥ÀzÀ 0 DVgÀ¯ÉèÉÃPÀÄ.)
p+3 = 0 CxÀªÁ p-2 = 0
p= -3 CxÀªÁ p
=2 EªÀÅ ¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼ÀÄ.
vÁ¼É:
p=2 DzÁUÀ,
JqÀ¨sÁUÀ: 22+2-6 =4+2-6 = 0 = §®¨sÁUÀ.
p = -3 DzÁUÀ,
JqÀ¨sÁUÀ: (-3)2 -3- 6 = 9-3-6 = 0 §®¨sÁUÀ.
2.19.1 ¸ÀªÀĸÉå 2: ©r¹: 6y2+y
-15 = 0.
¥ÀjºÁgÀ:
FUÀ JqÀ§¢AiÀÄ£ÀÄß £ÁªÀÅ (ax+b)(cx+d)={
acx2 + x(ad+bc)+bd} gÀÆ¥ÀPÉÌ ¥ÀjªÀwð¸À¨ÉÃPÀÄ.
E°è ac=6, bd= -15, ad+bc =1 DVgÀ¨ÉÃPÀÄ.
¥Àj²Ã®£É¬ÄAzÀ a=3, c=2,
b=5, d= -3 DVgÀÄvÀÛzÉ.
6y2+y
-15
= 6y2+10y -9y -15
= 2y(3y+5)-3(3y+5) – ¸ÁªÀiÁ£Àå ¥ÀzÀ3y+5 ªÀ£ÀÄß
ºÉÆgÀ vÉUÉzÁUÀ
= (3y+5)(2y-3)
6 y2+y
-15 =0 DVgÀĪÀÅzÀjAzÀ
(3y+5)(2y-3) =0
3y+5 = 0 CxÀªÁ 2y-3 =0
y = -5/3 CxÀªÁ y
=3/2EªÀÅ ¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼ÀÄ.
vÁ¼É:
y=3/2 DzÁUÀ, JqÀ§¢ = 6*9/4
+3/2 -15
=27/2+3/2 -15
= (27+3)/2 – 15 = 0 = §®§¢
EzÉÃjÃw y= -5/3 DzÁUÀ
vÁ¼É£ÉÆÃr.
2.19.1 ¸ÀªÀĸÉå 3: ©r¹: 13m = 6(m2+1)
¥ÀjºÁgÀ:
6m2-13m+6
=0
FUÀ JqÀ¨sÁUÀªÀ£ÀÄß
(ax+b)(cx+d)={ acx2 + x(ad+bc)+bd} gÀÆ¥ÀPÉÌ
vÀgÀ¨ÉÃPÀÄ.
E°è ac=6, bd= 6, ad+bc = -13 DVgÀ¨ÉÃPÀÄ.
¥Àj²Ã®£É¬ÄAzÀ a=3,
c=2,b=5,d= -3
i.e 6m2-13m+6=0
= 6m2-9m -4m+6
= 3m(2m -3) -2(2m-3) ------à ¸¸ÁªÀiÁ£Àå ¥ÀzÀ2m-3ªÀ£ÀÄß ºÉÆgÀvÉUÉzÁUÀ
= (2m-3)(3m-2)
6m2-13m+6 =0
(2m-3)(3m-2)=0
2m-3 = 0
CxÀªÁ 3m-2 =0
m = 3/2 CxÀªÁ m
=2/3 EªÀÅ zÀvÀÛ ¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼ÀÄ.
vÁ¼É:
m=2/3 DzÁUÀ,
JqÀ¨sÁUÀ = 6*4/9 -13*2/3 +6
= 8/3 -26/3+6
=(8-26)/3 +6 = 0 =§®¨sÁUÀ.
m= 3/2 DzÁUÀ vÁ¼É
£ÉÆÃr.
ªÉÄð
«ªÀj¹zÀAvÀºÀ «zsÁ£ÀPÉÌ vÀÄA¨Á C¨sÁå¸À ºÁUÀÆ ¸ÀªÀÄAiÀĪÀǨÉÃPÀÄ.»ÃVgÀĪÁUÀ KPÉ
¸ÀÆvÀæªÉÇAzÀ£ÀÄß PÀAqÀÄ»rAiÀĨÁgÀzÀÄ?
2.19.1 ¸ÀªÀĸÉå 4: 2x2+3x+1 =0 J£ÀÄߪÀÅzÀ£ÀÄß ©r¸ÀĪÁ.
|
CA. |
ºÀAvÀ |
«ªÀgÀuÉ |
|
1 |
x2
+(3/2)x+ (1/2) =0 |
JgÀqÀÆ
§¢UÀ¼À£ÀÄß 2 jAzÀ ¨sÁV¹zÉ. |
|
2 |
x2+(3/2)x=
-(1/2) |
(1/2) £ÀÄß §®§¢UÉ vÀA¢zÉ. |
|
(x+a)2
= x2+2ax+ a2 J£ÀÄߪÀ ¸ÀÆvÀæªÀ£ÀÄß G¥ÀAiÉÆÃV¸ÀĪÀ ºÁVzÀÝ°è ªÀÄÆ®ªÀ£ÀÄß
PÀAqÀÄ»rAiÀħºÀÄzÀÄ. »ÃVgÀĪÁUÀ 2ax = (3/2)x JAzÀÄ w½AiÀħºÀÄzÀÄ. |
||
|
3 |
x2+(3/2)x+ (3/4)2 = -(1/2)+
(3/4)2 |
(3/4)2 £ÀÄß JgÀqÀÆ §¢UÀ½UÉ PÀÆr¹zÉ. |
|
4 |
LHS =
x2 +2(3/4)x +
(3/4)2= [x+(3/4)]2 |
p2+2pq+q2
= (p+q)2 E°è p=x, q= 3/4 |
|
5 |
RHS = -(1/2)+ (3/4)2 =-(1/2)+ (9/16)= (1/16) |
¸ÁªÀiÁ£Àå
bÉÃzÀ 4*4=16 |
|
6 |
[x+(3/4)]2=(1/16) |
ºÀAvÀ 4ªÀÄvÀÄÛ
5jAzÀ LHS=RHS |
|
7 |
(x+(3/4)) = |
ºÀAvÀ 6 gÀ ªÀUÀðªÀÄÆ® |
|
8 |
x = -(3/4) |
3/4 £ÀÄß ªÀUÁðAvÀj¹ |
ªÉÄ𠫪Àj¹zÀAvÀºÀ «zsÁ£ÀzÀAvÉ
ax2
+bx+ c =0 zÀ ªÀÄÆ® PÀAqÀÄ»rAiÀÄĪÁ.
ªÀUÀð¸À«ÄÃPÀgÀtzÀ
ªÀÄÆ®UÀ¼À£ÀÄß PÀAqÀÄ»rAiÀÄĪÀ ¸ÀÆvÀæ(Formula for finding roots of
the quadratic equation)
ªÀUÀð
¸À«ÄÃPÀgÀtzÀ ¸ÁªÀiÁ£Àå gÀÆ¥À: ax2 +bx+ c =0,E°è a, b, c UÀ¼ÀÄ
ªÁ¸ÀÛ«PÀ ¸ÀASÉåUÀ¼ÁVzÀÄÝ a 0, b 0. F
¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼À£ÀÄß PÀAqÀÄ»rAiÀÄĪÁ.
|
CA. |
ºÀAvÀ |
«ªÀgÀuÉ |
|
1 |
x2
+(bx/a)+ (c/a) =0 |
JgÀqÀÆ
§¢UÀ¼À£ÀÄß ‘a’¬ÄAzÀ ¨sÁV¹zÉ. |
|
2 |
x2
+(bx/a) = -( c/a) |
c/a AiÀÄ£ÀÄß §®§¢UÉ vÀA¢zÉ. |
|
3 |
x2 +(bx/a) + (b/2a)2 = -( c/a) + (b/2a)2 |
(b/2a)2 ªÀ£ÀÄß JgÀqÀÆ §¢UÀ½UÉ PÀÆr¹zÉ. |
|
4 |
LHS= x2 +(bx/a) + (b/2a)2=
[x+(b/2a)]2 |
p2+2pq+q2
= (p+q)2 E°è p=x, q= b/2a |
|
5 |
RHS = b2/4a2- c/a=
(b2-4ac)/ 4a2 |
¸ÁªÀiÁ£Àå
bÉÃzÀ 4a2 |
|
6 |
[x+(b/2a)]2
=(b2-4ac)/ 4a2 |
ºÀAvÀ 4ªÀÄvÀÄÛ
5jAzÀ LHS=RHS |
|
7 |
x+(b/2a) = = |
ºÀAvÀ 6 gÀ ªÀUÀðªÀÄÆ® |
|
8 |
x = [-b |
b/2a £ÀÄß RHS UÉ ¥ÀPÁëAvÀj¹. |
ax2 +bx+ c =0 ¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼ÀÄ:
x = [-b +(b2-4ac)]/2a ªÀÄvÀÄÛ x = [-b -(b2-4ac)]/2a
UÀªÀĤ¹:
F
¸ÀÆvÀæªÀ£ÀÄß ªÀUÀð¸ÀÆvÀæ J£ÀÄߪÀgÀÄ ªÀÄvÀÄÛ EzÀ£ÀÄß ¥Àæ¥ÀæxÀªÀĪÁV ¨sÁgÀwÃAiÀÄ UÀtÂvÀdÕ ²æÃzsÀgÁZÁAiÀÄð gÀÄ(1025AD)
¥ÀjZÀ¬Ä¹gÀÄvÁÛgÉ. EzÀ£ÀÄß ±ÉÆèÃPÀgÀÆ¥ÀzÀ°è °Ã¯ÁªÀwAiÀÄ®Æè PÉÆnÖzÉ(±ÉÆèÃPÀ 67)
2.19.1 ¸ÀªÀĸÉå 5: ©r¹: 4x2+8x+4
= 0
¥ÀjºÁgÀ:
E°è FUÀ, a =4, b=8, c
=4
b2-4ac
= 64 – 4*4*4 = 0
(b2-4ac)
= (0)
= 0
ªÀÄÆ®UÀ¼ÀÄ: p = [-b +
]/2a =(-8+0)/8
= - 1
CxÀªÁ
p
= [-b -]/2a = (-8-0)/8 =
- 1
E°è ªÀÄÆ®UÀ¼ÀÄ ¸ÀªÀĪÁVªÉ: -
1
UÀªÀĤ¹: 4x2+8x+4 = 4(x2+2x+1) =
4(x+1)(x+1). F ¥ÀæPÁgÀªÀÇ x=-1 ªÀÄÆ®ªÉÃ
DVzÉ.
2.19.1 ¸ÀªÀĸÉå 6: ©r¹: p2+p-6 = 0(2.19.1.1 gÀ°è ªÀiÁrzÀ
¯ÉPÀ̪Éà EzÁVzÉ.)
¥ÀjºÁgÀ:
¸À«ÄÃPÀgÀtªÀÅ
ax2
+bx+ c =0 gÀÆ¥ÀzÀ°èzÉ.
a =1, b=1, c =-6
b2-4ac
= 1 – 4*1*(-6) = 25
= (25)
= 5
¸ÀÆvÀæzÀAvÉ:
p = [-b +]/2a =(-1+5)/2
= 2 CxÀªÁ
p = [-b -]/2a = (-1-5)/2 =
-3
F ªÀÄÆ®UÀ¼ÀÄ F »AzÉAiÉÄÃ
zÉÆgÉwªÉ (2.19.1.1)
2.19.1 ¸ÀªÀĸÉå 7: ©r¹: 6y2+y
-15 = 0 (2.19.1.2gÀ°è ªÀiÁrzÉ)
¥ÀjºÁgÀ:
¸À«ÄÃPÀgÀtªÀÅ
ax2
+bx+ c =0 gÀÆ¥ÀzÀ°èzÉ.
a=6, b=1, c= -15
b2-4ac
= 1 – 4*6*(-15) = 361
(b2-4ac)
= (361)
= 19
¸ÀÆvÀæzÀAvÉ,
y = [-b +]/2a =(-1+19)/12
= 18/12= 3/2 CxÀªÁ
y = [-b -]/2a = (-1-19)/12 = -20/12 = -5/3
F ªÀÄÆ®UÀ¼À£ÀÄß £ÁªÀÅ F
»AzÉAiÉÄà ¥ÀqÉ¢zÉÝêÉ.
3/2 ªÀÄvÀÄÛ -5/3 ªÀÄÆ®UÀ¼ÀÄ
DVgÀĪÀÅzÀjAzÀ (y-3/2)(y+5/3) C¥ÀªÀvÀð£ÀUÀ¼ÀÄ
DVªÉ.
(y-3/2)(y+5/3) = (2y-3)(3y+5)/6
6y2+y
-15 = (2y-3)(3y+5)
ZÀlĪÀnPÉ: 2.19.1.3 gÀ°è PÉÆlÖ
¸ÀªÀĸÉåAiÀÄ£ÀÄß ¸ÀÆvÀæ G¥ÀAiÉÆÃV¹ ©r¹.
2.19.1 ¸ÀªÀĸÉå 8: ©r¹: y2-2y+2 =0
¥ÀjºÁgÀ:
zÀvÀÛ
¸À«ÄÃPÀgÀtªÀÅ ax2 +bx+ c =0 gÀÆ¥ÀzÀ°èzÉ.
a=1, b=-2, c=2
b2-4ac
= 4 – 4*1*2 = -4
(b2-4ac)
= (-4)
= 2
¸ÀÆvÀæzÀAvÉ,
y = [-b +]/2a =(2+2)/2 = 1+CxÀªÁ
y = [-b -]/2a = (2-2)/2 = 1-
ªÀÄÆ®UÀ¼ÀÄ
ªÁ¸ÀÛªÀ ¸ÀASÉåUÀ¼À®è.
vÁ¼É:
zÀvÀÛ
¸À«ÄÃPÀgÀtzÀ°è y= 1+£Àß DzÉò¹,
y2-2y+2 = (1+)2
-2(1+) +2 ((1+)2 («¸ÀÛj¸À®Ä (a+b)2
=a2+b2+2ab ¸ÀÆvÀæ
G¥ÀAiÉÆÃV¹)
= [1 +(-1) +2] +[-2 -2] +2
= 1-1 +2-2 -2+2 = 0 = §®§¢.
EzÉà jÃw E£ÉÆßAzÀÄ ªÀÄÆ® = 1-PÀÆÌ
vÁ¼É£ÉÆÃr.
2.19.1 ¸ÀªÀĸÉå 9: ©r¹: 2(3y-1)/(4y-3) = 5y/(y+2) -2
¥ÀjºÁgÀ:
§®§¢= [5y -2(y+2)]/(y+2) =
(3y-4)/(y+2)
FUÀ £ÁªÀÅ ©r¸À¨ÉÃPÁzÀzÀÄÝ: 2(3y-1)/(4y-3)
= (3y-4)/(y+2)
CqÀØ UÀÄuÁPÁgÀ¢AzÀ, 2(3y-1)*(y+2)
= (3y-4)*(4y-3)
2(3y2+6y –y -2) = 12y2-9y
-16y+12
6y2+10y
-4 = 12y2-25y +12(¥ÀPÁëAvÀj¹zÁUÀ)
6y2-35y +16=0
FUÀ F ¸À«ÄÃPÀgÀtªÀÅ ax2
+bx+ c =0 gÀÆ¥ÀzÀ°èzÉ.
E°è a=6, b=-35, c= 16
b2-4ac
= 1225 – 4*6*16 = 1225-384 = 841
(b2-4ac)
= (841)
= 29
¸ÀÆvÀæzÀAvÉ,
y = [-b +]/2a =(35+29)/12
= 16/3 CxÀªÁ
y = [-b -]/2a = (35-29)/12 = 1/2
vÁ¼É
zÀvÀÛ
¸À«ÄÃPÀgÀtzÀ°è F ¨É¯ÉUÀ¼À£ÀÄß ºÁQ vÁ¼É £ÉÆÃr.
2.19.1 ¸ÀªÀĸÉå 10: ©r¹: (y-1)(5y+6)
/(y-3) = (y-4)(5y+6)/(y-2)
¥ÀjºÁgÀ:
¸À«ÄÃPÀgÀtzÀ°è
CqÀØ UÀÄuÁPÁgÀ ªÀiÁrzÁUÀ,
(y-1)(5y+6)(y-2) = (y-4)(5y+6)(y-3)
JqÀ¨sÁUÀ = (5 y2+6y-5y-6)(y-2)
= (5 y2+y-6)(y-2)
= 5 y3+ y2-6y -10 y2-2y+12
=5 y3 -9y2-8y+12
§®¨sÁUÀ = (5y2+6y-20y-24)(y-3)
= (5y2-14y -24)(y-3)
= 5y3-14 y2-24y -15y2+42y+72
= 5y3-29y2+18y+72
JqÀ¨sÁUÀ = §®¨sÁUÀ
5 y3 -9y2-8y+12= 5y3-29y2+18y+72.
(¥ÀPÁëAvÀj¹zÁUÀ)
5 y3 -9y2-8y+12-(5y3-29y2+18y+72)
=0
20y2-26y-60 = 0 ( 2 £ÀÄß
ºÉÆgÀvÉUÀzÁUÀ)
10y2-13y-30 = 0
FUÀ ¸À«ÄÃPÀgÀt: ax2
+bx+ c =0 gÀÆ¥ÀzÀ°èzÉ.
a=10, b=-13, c= -30
b2-4ac
= 169 – 4*10*(-30) = 169+1200 = 1369
(b2-4ac)
= (1369)
= 37
¸ÀÆvÀæzÀAvÉ,
y = [-b +]/2a =(13+37)/20
= 50/20 = 5/2 CxÀªÁ
y = [-b -]/2a = (13-37)/20 = -24/20 = -6/5
vÁ¼É:
yAiÀÄ ¨É¯ÉAiÀÄ£ÀÄß
¸À«ÄÃPÀgÀtzÀ°è DzÉò¹ LHS = RHS §gÀÄvÀÛzÉ.
ªÉÄð£À
¸ÀªÀĸÉåAiÀÄ£ÀÄß ©r¸ÀĪÀ ¥ÀAiÀiÁðAiÀÄ «zsÁ£À:-
zÀvÀÛ ¸À«ÄÃPÀgÀtzÀ°è (5y+6) ¸ÁªÀiÁ£Àå
C¥ÀªÀvÀð£À, £ÀªÀÄVÃUÀ 2 DAiÉÄÌUÀ½ªÉ:- CAzÀgÉ
(1) 5y+6 = 0:
DUÀ 5y= -6 y = -6/5
y = -6/5 JA§ÄzÀÄ zÀvÀÛ
¸ÀªÀĸÉåAiÀÄ ¥ÀjºÁgÀ ---------à(1)
(2) 5y+6 0 DzÀgÉ, 5y+6 jAzÀ JgÀqÀÆ
§¢UÀ¼À£ÀÄß ¨sÁV¹,
[(y-1)/(y-3)] =[(y-4)/(y-2)] :
CqÀØ UÀÄuÁPÁgÀ ªÀiÁr,
(y-1)(y-2)
= (y-4)(y-3)
CAzÀgÉ y2-2y-y+2 = y2-3y-4y+12
CAzÀgÉ y2-3y+2 = y2-7y+12: (¥ÀPÁëAvÀj¹zÁUÀ)
CAzÀgÉ y2-3y+2-( y2-7y+12)=0
CAzÀgÉ y2-3y+2-y2+7y-12=0
CAzÀgÉ 4y-10=0
CAzÀgÉ 4y=10 or y=10/4 =5/2
---------------------------à(2)
(1) ªÀÄvÀÄÛ (2) jAzÀ, zÀvÀÛ
¸À«ÄÃPÀgÀtzÀ ªÀiË®åUÀ¼ÀÄ: 5/2 ªÀÄvÀÄÛ -6/5
2.19.1 ¸ÀªÀĸÉå 11: y/(y+1) +
(y+1)/y = 25/12
¥ÀjºÁgÀ:
zÀvÀÛ
¸À«ÄÃPÀgÀtzÀ JqÀ§¢AiÀÄ£ÀÄß ¸ÀÄ®©üÃPÀj¹zÁUÀ,
[y*y +(y+1)(y+1)]/[y(y+1)]
= (y2+y2+2y+1)/( y2+y)
LHS = RHS
DVgÀĪÀÅzÀjAzÀ
(y2+y2+2y+1)/( y2+y)
= 25/12
CqÀØ UÀÄuÁPÁgÀ ªÀiÁr,
12(y2+y2+2y+1) = 25( y2+y)
24y2+24y+12
= 25y2+25y.
JqÀ§¢AiÀÄ°ègÀĪÀÅzÀ£ÀÄß §®§¢UÉ
PÉÆAqÀĺÉÆÃV.
0 = y2+y-12
F ¸À«ÄÃPÀgÀtªÀÅ ax2
+bx+ c =0 gÀÆ¥ÀzÀ°èzÉ.
a=1, b=1, c= -12
b2-4ac
= 1 – 4*1*(-12) = 1+48 = 49
= (49)
= 7
¸ÀÆvÀæzÀAvÉ, ªÀÄÆ®UÀ¼ÀÄ:
y = [-b +)]/2a =(-1+7)/2
= 3
CxÀªÁ
y = [-b -)]/2a = (-1-7)/2 =
- 4
vÁ¼É:
F
¨É¯ÉUÀ¼À£ÀÄß zÀvÀÛ ¸À«ÄÃPÀgÀtzÀ°è DzÉò¹zÁUÀ JqÀ§¢=§®§¢ §gÀÄvÀÛzÉ.
2.19.1 ¸ÀªÀĸÉå 12 : ©r¹: (3x2-5x+2)
(3x2-5x-2)=21
¥ÀjºÁgÀ:
1. 3x2-5x
= y DVgÀ°, DUÀ zÀvÀÛ ¸À«ÄÃPÀgÀt: (y+2) (y-2) =21
y2 – 4 = 21
y2 = 21+4 =25
y =(25)= 5
2. y = 3x2-5x =5
3x2-5x
5=0
x = - (-5) (25+60)/2*3
= 5 (85)/6
2.19.1 ¸ÀªÀĸÉå 13 (F «¨sÁUÀzÀ DgÀA¨sÀzÀ°è PÉÆlÖ
¸ÀASÉå): ¤ÃªÀÅ ¤ªÀÄä
¸ÉßûvÀgÉÆqÀUÀÆr MAzÀÄ ¥ÀæªÁ¸ÀPÉÌ ºÉÆÃUÀ®Ä ¤zsÀðj¸ÀÄwÛÃj. DºÁgÀPÁÌV MlÄÖ 480gÀÆ.
RZÁðUÀÄvÀÛzÉ. DzÀgÉ PÉÆ£É PÀëtzÀ°è ¤ªÀÄä 8 d£À ¸ÉßûvÀgÀÄ ¥ÀæªÁ¸ÀPÉÌ
§gÀ°®è. ºÁUÁV ¥ÀæwAiÉƧâgÀÆ DºÁgÀPÁÌV 10gÀÆ. ºÉaÑUÉ PÉÆqÀ¨ÉÃPÁ¬ÄvÀÄ. ºÁUÁzÀgÉ
PÉÆ£ÉAiÀÄ°è ¥ÀæwAiÉƧâgÀÆ PÉÆlÖ ºÀt JµÀÄÖ?
¥ÀjºÁgÀ:
¥ÀæªÁ¸ÀPÉÌ
ºÉÆÃUÀ®Ä ªÉÆzÀ®Ä ¤zsÀðj¹zÀªÀgÀ ¸ÀASÉå: ‘x’
DUÀ
DºÁgÀPÁÌV ¥ÀæwAiÉƧâjUÉ vÀUÀ®ÄªÀ ªÉZÀÑ: 480/x
8 d£À
¨ÁgÀ¢zÀÄÝzÀjAzÀ ¥ÀæªÁ¸ÀPÉÌ ºÉÆÃzÀªÀgÀ ¸ÀASÉå: (x-8)
FUÀ
¥ÀæwAiÉƧâjUÉ vÀUÀ®ÄªÀ ªÉZÀÑ = 480/(x-8)
F ºÀtªÀÅ
ªÀÄÄAZÉ ¤zsÀðj¹zÀ ºÀtPÁÌV 10gÀÆ. ºÉZÀÄÑ
ºÉƸÀzÀgÀ= ºÀ¼ÉzÀgÀ +10
480/(x-8) =
480/x + 10
480/(x-8) =
(480+10x)/x.
CqÀØ
UÀÄuÁPÁgÀ ªÀiÁr,
480x =
(480+10x)(x-8)
RHS= 480x
-480*8 +10x*x-80x
= 480x -
3840+ 10x2-80x =
10x2+400x-3840
0 =10x2+400x-3840-480x.
(¥ÀPÁëAvÀj¹zÁUÀ)
CxÀªÁ 10x2-80x-3840
=0
F ¸À«ÄÃPÀgÀtªÀ£ÀÄß 10 jAzÀ ¨sÁV¹.
x2-8x-384
=0
F ¸À«ÄÃPÀgÀtªÀÅ ax2
+bx+ c =0 gÀÆ¥ÀzÀ°èzÉ.
a=10, b= -80, c= -3840
b2-4ac
= 6400 – 4*10*(-3840) = 6400 +153600
=160000
= (160000)
= 40
¸ÀÆvÀæzÀAvÉ ªÀÄÆ®UÀ¼ÀÄ:
x = [
]
=(80+400)/20 = 24 CxÀªÁ
x = [-b -]/2a = (80-400)/20 = -16
d£ÀgÀ ¸ÀASÉåAiÀÄÄ IÄt
¸ÀASÉåAiÀiÁUÀĪÀÅ¢®è. DzÀÝjAzÀ x = 24
24 d£ÀgÀÄ ¥ÀæªÁ¸À ºÉÆÃUÀ®Ä
¤zsÀðj¹zÀÝgÀÄ.
PÉÆ£ÉAiÀÄ°è ¥ÀæwAiÉƧâgÀÄ
PÉÆqÀ¨ÉÃPÁzÀ ºÀt (=
) = 30gÀÆ.
vÁ¼É:
24 d£ÀgÀÄ
¥ÀæªÁ¸ÀPÉÌ ºÉÆÃUÀ®Ä ¤zsÀðj¹zÀÝgÀÄ.
¥ÀæwAiÉƧâgÀ
RZÀÄð = 480/24 = 20gÀÆ.
8 d£À
ºÉÆÃUÀ¢zÀÄÝzÀjAzÀ ¥ÀæªÁ¸ÀPÉÌ ºÉÆÃzÀªÀgÀÄ = 24 - 8 = 16
FUÀ
¥ÀæwAiÉƧâgÀ RZÀÄð = 480/16 = 30gÀÆ.
EzÀÄ
ªÉÆzÀ°zÀQÌAvÀ 10gÀÆ. ºÉZÀÄ.Ñ
GvÀÛgÀ
¸ÀªÀĸÉåUÉ vÁ¼ÉAiÀiÁUÀÄvÀÛzÉ.
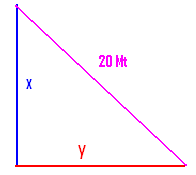
2.19.1 ¸ÀªÀĸÉå 14: MAzÀÄ ®A§PÉÆãÀ wæPÉÆãÀzÀ
«PÀtð 20«ÄÃlgï DVzÉ. G½zÉgÀqÀÄ ¨ÁºÀÄUÀ¼À ªÀåvÁå¸À 4«ÄÃlgï DzÀgÉ, DªÉgÀqÀÄ
¨ÁºÀÄUÀ¼À GzÀÝ PÀAqÀÄ»r.
¥ÀjºÁgÀ:
|
®A§PÉÆãÀ wæPÉÆãÀzÀ°è «PÀtð ©lÄÖ G½zÉgÀqÀÄ ¨ÁºÀÄUÀ¼ÀÄ x, y DVgÀ°. ¥ÉÊxÁUÉÆgÀ¸À£À ¥ÀæªÉÄÃAiÀÄzÀAvÉ, («PÀtð)2 = x2+ y2 . «PÀtð = 20«Ä. ¨ÁºÀÄUÀ¼ÉgÀqÀgÀ ªÀåvÁå¸À 4«Ä = x-y =
4: x= 4+y. x£À F
¨É¯ÉAiÀÄ£ÀÄß ¸À«ÄÃPÀgÀt (1)gÀ°è DzÉò¹, 400 = x2+ y2 =(4+y)2+ y2 =
(16+8y+ y2)+ y2 =16+8y+ 2y2. (¥ÀPÁëAvÀj¹zÁUÀ) 2y2+8y-384
= 0 F ¸À«ÄÃPÀgÀt ax2 +bx+ c =0 gÀÆ¥ÀzÀ°èzÉ. a=2, b= 8, c= -384.
¸ÀÆvÀæzÀAvÉ
ªÀÄÆ®UÀ¼ÀÄ: y = [-b + = (-8-56)/4 = -16 wæPÉÆãÀzÀ
¨ÁºÀÄ IÄt ¸ÀASÉåAiÀiÁUÀĪÀÅ¢®è. |
|
vÁ¼É:
(¨ÁºÀÄ)2+
(¨ÁºÀÄ)2 = 122+ 162 = 144+ 256 = 400 =202
.(«PÀtð)2
¸ÀªÀĸÉå
¥ÀjºÁgÀ ¸ÀjAiÀiÁVzÉ.
2.19.1 ¸ÀªÀĸÉå15: JgÀqÀÄ ¥ÀlÖtUÀ¼À £ÀqÀÄ«£À
zÀÆgÀ 1200Q.«Ä.. MAzÀÄ gÉÊ®ÄUÁrAiÀÄÄ F JgÀqÀÄ ¥ÀlÖtUÀ¼À £ÀqÀÄªÉ NqÀÄvÀÛªÉ. gÉÊ°£À
ªÉÃUÀªÀÅ ªÉÆzÀ°£À ªÉÃUÀQÌAvÀ 30Q.«Ä./UÀA. ºÉZÁÑzÀgÉ CzÀPÉÌ JgÀqÀÄ UÀAmÉ
¸ÀªÀÄAiÀÄ PÀrªÉÄ ¸ÁPÁUÀÄvÀÛzÉ. ºÁUÁzÀgÉ gÉÊ°£À ªÉÆzÀ°£À ªÉÃUÀ JµÀÄÖ?
¥ÀjºÁgÀ:
gÉÊ°£À ªÉÆzÀ°£À ªÉÃUÀ = xDVgÀ°.
NqÀ®Ä ¨ÉÃPÁzÀ ¸ÀªÀÄAiÀÄ = 1200/x UÀA.
ªÉÃUÀªÀÅ 30 Q.«Ä./UÀA.
ºÉZÁÑzÀgÉ JgÀqÀ£Éà ªÉÃUÀzÀ°è ¨ÉÃPÁzÀ ¸ÀªÀÄAiÀÄ = 1200/(x+30).UÀA.
ºÉƸÀ
¸ÀªÀÄAiÀĪÀÅ ªÀÄÄAa£À ¸ÀªÀÄAiÀÄQÌAvÀ 2 UÀAmÉ PÀrªÉÄ.
1200/x-1200/(x+30)
= 2
ZÀlĪÀnPÉ: ¸ÀAPÉëæ¹, ¸ÀÆvÀæ G¥ÀAiÉÆÃV¹
ªÀÄÆ®UÀ¼À£ÀÄß PÀAqÀÄ»r¬Äj: x=120
vÁ¼É:
1200/120 –
1200/150 = 10-8 =2 zÀvÁÛA±À.
2.19.1 ¸ÀªÀĸÉå 16: M§â £Á«PÀ£ÀÄ
MAzÀÄ ªÉÆÃmÁgÀÄ zÉÆÃtÂAiÀÄ£ÀÄß JgÀqÀÄ §AzÀgÀÄUÀ¼À £ÀqÀÄªÉ ZÀ¯Á¬Ä¸ÀÄvÁÛ£É.
§AzÀgÀÄUÀ¼À £ÀqÀÄ«£À zÀÆgÀ 8 Q.«Ä. CªÀ£ÀÄ MAzÀÄ §AzÀj¤AzÀ ºÉÆgÀlÄ E£ÉÆßAzÀÄ
§AzÀjUÉ ºÉÆÃV ¥ÀÅ£ÀB ªÁ¥Á¸ÀÄ §gÀ®Ä 1UÀA 40¤«ÄµÀUÀ¼ÀÄ ¨ÉÃPÀÄ. ¥ÀæªÁºÀzÀ ªÉÃUÀ UÀAmÉUÉ 2 Q.«Ä. DzÀgÉ,
¤±ÀÑ® ¤Ãj£À°è zÉÆÃtÂAiÀÄ ªÉÃUÀ JµÀÄÖ?
[zÉÆÃtÂAiÀÄÄ
¥ÀæªÁºÀzÀ eÉÆvÉUÉà ZÀ°¸ÀĪÁUÀ ¸ÀªÀÄAiÀÄ PÀrªÉÄ ¸ÁPÀÄ. ¥ÀæªÁºÀzÀ «gÀÄzÀÞ
ZÀ°¸ÀĪÁUÀ ¸ÀªÀÄAiÀÄ eÁ¹Û¨ÉÃPÀÄ]
¥ÀjºÁgÀ:
zÉÆÃtÂAiÀÄ
ªÉÃUÀ = xDVgÀ° (¤±ÀÑ® ¤Ãj£À°è)
ºÉÆÃV, §gÀ®Ä
¨ÉÃPÁzÀ MlÄÖ ¸ÀªÀÄAiÀÄ 1UÀA. 40¤. = 100/60 =
5/3 UÀAmÉ.
§AzÀgÀÄUÀ¼À
£ÀqÀÄ«£À zÀÆgÀ = 8Q.«Ä.
¥ÀæªÁºÀzÀ
ªÉÃUÀ 2Q.«Ä/UÀA.
¥ÀæªÁºÀzÀ
¢QÌ£À°è ºÉÆÃUÀ®Ä ¨ÉÃPÁzÀ PÁ® = 8/x+2 (zÉÆÃtÂAiÀÄ ªÉÃUÀ + ¥ÀæªÁºÀzÀ
ªÉÃUÀ)
¥ÀæªÁºÀzÀ
«gÀÄzÀÞ ºÉÆÃUÀ®Ä ¨ÉÃPÁzÀ PÁ® = 8/x-2 (¥ÀæªÁºÀªÀÅ ªÉÃUÀªÀ£ÀÄß PÀrªÉÄ ªÀiÁqÀÄvÀÛzÉ)
MlÄÖ
¸ÀªÀÄAiÀÄ = 8/(x-2) + 8/(x+2) = 5/3
DzÀÄzÀjAzÀ
©r¸À¨ÉÃPÁzÀÄÝ: 8/(x-2) +
8/(x+2) = 5/3
ZÀlĪÀnPÉ: ¸À«ÄÃPÀgÀtªÀ£ÀÄß ¸ÀÄ®©üÃPÀj¹,
¸ÀÆvÀæ G¥ÀAiÉÆÃV¹ ªÀÄÆ® PÀAqÀÄ »r¬Äj x =10
vÁ¼É:
¨ÉÃPÁzÀ MlÄÖ
PÁ® = 8/(10-2) + 8/(10+2) = 8/8 + 8/12 = 1+2/3 = 5/3 zÀvÁÛA±À
2.19.1 ¸ÀªÀĸÉå 17: MAzÀÄ
«ªÀiÁ£ÀªÀÅ ¤UÀ¢vÀ ¸ÀªÀÄAiÀÄQÌAvÀ 30 ¤«ÄµÀ vÀqÀªÁV ºÉÆgÀnvÀÄ. CzÀÄ
¥ÀAiÀÄt¸À¨ÉÃPÁzÀ zÀÆgÀ 1500 Q.«Ä. ¤UÀ¢vÀ ¸ÀªÀÄAiÀÄPÉÌÃ
C°èUÉ vÀ®Ä¥À®Ä CzÀÄ vÀ£Àß ªÉÃUÀªÀ£ÀÄß ªÀiÁªÀÄÆ®Ä ªÉÃUÀQÌAvÀ 250Q.«Ä. £ÀµÀÄÖ
ºÉaѸÀ¨ÉÃPÀÄ. ºÁUÁzÀgÉ CzÀgÀ ªÀiÁªÀÄÆ®Ä ªÉÃUÀ ªÀÄvÀÄÛ ªÀiÁªÀÄÆ®Ä CªÀ¢ü
PÀAqÀÄ»r¬Äj.
¥ÀjºÁgÀ:
«ªÀiÁ£ÀzÀ
¤vÀåzÀ ªÉÃUÀ = x DVgÀ°.
PÀæ«Ä¸À¨ÉÃPÁzÀ
zÀÆgÀ = 1500Q.«Ä.
ªÀiÁªÀÄÆ° ¥ÀæAiÀiÁtzÀ ¸ÀªÀÄAiÀÄ = zÀÆgÀ/ ªÉÃUÀ = 1500/x UÀAmÉ.
«ªÀiÁ£ÀªÀÅ
CzsÀð UÀAmÉ vÀqÀªÁV ºÉÆgÀnzÉ. ¤UÀ¢vÀ ªÉüÉUÉà UÀÄj vÀ®Ä¥À®Ä CzÀÄ vÀ£Àß
ªÉÃUÀªÀ£ÀÄß ºÉaѹPÉƼÀî¯ÉèÉÃPÀÄ.
FUÀ
«ªÀiÁ£ÀPÉÌ ¥ÀAiÀÄt¸À®Ä EgÀĪÀ ¸ÀªÀÄAiÀÄ = (1500/x) -1/2
EzÉÃ
¸ÀªÀÄAiÀÄzÀ°è «ªÀiÁ£À 1500 Q.«Ä. ºÁjzÉ. DUÀ ªÉÃUÀ: (x+250)
zÀÆgÀ= ¸ÀªÀÄAiÀÄ*ºÉƸÀ ªÉÃUÀ
I.e. 1500 =
{(1500/x) -1/2}*(x+250) = (3000-2x)*(x+250)/2x
I.e. 3000x =
(3000-x)(x+250)
CqÀØ
UÀÄuÁPÁgÀ¢AzÀ,
I.e. 3000x =
3000x -x2+750000-250x
I.e. x2-750000+250x
=0
¸ÀÆvÀæ
G¥ÀAiÉÆÃV¹: = 1750
ªÀÄÆ®UÀ¼ÀÄ:
x = [-b )]/2a = (-250 1750)/2
x = 750 CxÀªÁ x =-1000
«ªÀiÁ£ÀzÀ
ªÉÃUÀ IÄt ¨É¯É CxÀð«®èzÀÄÝ x = 750Q.«Ä/UÀAmÉ
ªÀiÁªÀÄÆ° ¥ÀæAiÀiÁtzÀ ¸ÀªÀÄAiÀÄ= 1500/750 =
2UÀAmÉ
vÁ¼É:
«ªÀiÁ£ÀzÀ
ªÉÃUÀ 250Q.«Ä. ºÉZÁÑzÀÄzÀjAzÀ ºÉƸÀ ªÉÃUÀ: 1000Q.«Ä. /UÀAmÉ.
1500Q.«Ä. PÀæ«Ä¸À®Ä ¨ÉÃPÁzÀ
¸ÀªÀÄAiÀÄ = 1500/1000 = 1.5 UÀAmÉ. CAzÀgÉ
¤UÀ¢vÀ
¥ÀæAiÀiÁtzÀ ªÉüÉVAvÀ ½ UÀAmÉ PÀrªÉÄ.
«ªÀiÁ£ÀªÀÅ ½ UÀAmÉ
vÀqÀªÁV ºÉÆgÀngÀĪÀÅzÀjAzÀ, ¸ÀjAiÀiÁzÀ ªÉüÉUÉà UÀÄjAiÀÄ£ÀÄß vÀ®¥ÀÅvÀÛzÉ.
¸ÀªÀĸÉå ¥ÀjºÁgÀ ¸ÀjAiÀiÁVzÉ.
2.19.1 ¸ÀªÀĸÉå 18: K ºÀÄqÀÄV,
ºÀA¸ÀUÀ¼À UÀÄA¦£À MlÄÖ ºÀA¸ÀUÀ¼À ªÀUÀðªÀÄÆ®zÀ 7/2 gÀµÀÄÖ ºÀA¸ÀUÀ¼ÀÄ PÉƼÀzÀ
zÀqÀzÀ°è DqÀÄwÛªÉ. G½zÉgÀqÀÄ ºÀA¸ÀUÀ¼ÀÄ PÉƼÀzÀ°è dUÀ¼ÀªÁqÀÄwÛªÉ. ºÁUÁzÀgÉ MlÄÖ
EgÀĪÀ ºÀA¸ÀUÀ¼ÉµÀÄÖ? (°Ã¯ÁªÀw ±ÉÆèÃPÀ 70)
¥ÀjºÁgÀ:
MlÄÖ
ºÀA¸ÀUÀ¼À ¸ÀASÉå x DVgÀ°.
zÀqÀzÀ°è
DqÀÄwÛgÀĪÀ ºÀA¸ÀUÀ¼ÀÄ = (7/2)
PÉƼÀzÀ°è
dUÀ¼ÀªÁqÀĪÀ ºÀA¸ÀUÀ¼ÀÄ = 2
x= (7/2)+2
F
¸À«ÄÃPÀgÀtªÀ£ÀÄß ©r¹zÁUÀ, ªÀÄÆ®UÀ¼ÀÄ: 1/4 CxÀªÁ 16
DzÀgÉ
ºÀA¸ÀUÀ¼À ¸ÀASÉå 1/4 EgÀ¯ÁUÀzÀÄ. MlÄÖ EgÀĪÀ ºÀA¸ÀUÀ¼ÀÄ = 16
vÁ¼É:
16 = 14+2 =
(7/2) +2 ¸ÀªÀĸÉåAiÀÄ°è PÉÆlÖAvÉAiÉÄà EzÉ.
2.19.1 ¸ÀªÀĸÉå 19: CdÄð£À£ÀÄ ªÀĺÁ¨sÁgÀvÀ AiÀÄÄzÀÞzÀ°è PÀtð£À£ÀÄß PÉÆ®è®Ä §vÀÛ½PÉ ¬ÄAzÀ
ºÀ®ªÀÅ ¨ÁtUÀ¼À£ÀÄß vÉUÉAiÀÄÄvÁÛ£É. vÉUÉzÀ ¨ÁtUÀ¼À°è CzsÀðzÀµÀÖjAzÀ PÀtð£À
¨ÁtUÀ¼À£ÀÄß vÀÄAqÀj¸ÀÄvÁÛ£É. vÉUÉzÀ ¨ÁtUÀ¼À ªÀUÀðªÀÄÆ®zÀ 4 gÀµÀÖjAzÀ PÀtð£À PÀÄzÀÄgÉUÀ¼À£ÀÄß, 6 ¨ÁtUÀ½AzÀ ±À®å£À£ÀÄß, MAzÉÆAzÀjAzÀ PÀtð£À gÀxÀzÀ PÉÆqÉ, PÀtð£À gÀxÀzÀ
¨ÁªÀÅl, ªÀÄvÀÄÛ PÀtð£À ©®è£ÀÄß vÀÄAqÀj¸ÀÄvÁÛ£É. G½zÀ MAzÀÄ ¨Át¢AzÀ PÀtð£À£ÀÄß
PÉÆAzÀgÉ, §vÀÛ½PÉ ¬ÄAzÀ MlÄÖ JµÀÄÖ ¨ÁtUÀ¼À£ÀÄß vÉUÉAiÀÄÄvÁÛ£É? (°Ã¯ÁªÀw: ±ÉÆèÃPÀ 71)
¥ÀjºÁgÀ:
vÉUÉzÀ ¨ÁtUÀ¼À MlÄÖ ¸ÀASÉå x EgÀ°.
|
ºÀAvÀ |
KvÀPÉÌ |
JµÀÄÖ |
|
1 |
PÀtð£À ¨ÁtUÀ¼À£ÀÄß
PÀvÀÛj¸À®Ä |
(x/2) |
|
2 |
PÀtð£À PÀÄzÀÄgÉUÀ½UÁV |
4 |
|
3 |
±À®å¤UÉ |
6 |
|
4 |
gÀxÀzÀ
PÉÆqÉ,¨ÁªÀÅl,PÀtð£À ©®ÄèUÀ½UÉ |
(1+1+1) =3 |
|
5 |
PÀtð£À ªÉÄÃ¯É |
1 |
x = (x/2)+ 4 +6+3+1
x –(x/2)-10 = 4
(x/2)-10 = 4
(x-20) = 8
x2-40x+400
= 64x --------à ((a+b)2 ¸ÀÆvÀæ G¥ÀAiÉÆÃV¹zÉ).
x2-104x+400
=0
(x-100)*(x-4) =0
x=100 CxÀªÁ x=4
(CªÀ£ÀÄ 6 ¨ÁtUÀ¼À£ÀÄß ±À®å¤UÉ
G¥ÀAiÉÆÃV¹gÀĪÀÅzÀjAzÀ 4 ¸ÁzsÀå«®è)
DzÀÄzÀjAzÀ CdÄð£À£ÀÄ 100
¨ÁtUÀ¼À£ÀÄß vÉUÉ¢gÀÄvÁÛ£É
vÁ¼É:
100=
50+40+6+3+1
2.19.1 ¸ÀªÀĸÉå 20:MAzÀÄ PÁr£À ªÀÄzsÀåzÀ°è ªÀÄAUÀUÀ¼À UÀÄA¦£À 1/5 £Éà ¨sÁUÀzÀ°è 3 £ÀÄß
PÀ¼ÉzÀÄ ªÀVð¹zÀ UÀÄA¥ÀÅ UÀĺÉUÉ ºÉÆìÄvÀÄ. G½zÀ MAzÀÄ ªÀÄgÀzÀ gÉA¨ÉAiÀÄ£ÀÄß
ºÀwÛvÀÄ. ªÀÄAUÀUÀ¼À MlÄÖ ¸ÀASÉå JµÀÄÖ? (¨sÁ¸ÀÌgÀ : ©ÃdUÀtÂvÀ)
¥ÀjºÁgÀ:
ªÀÄAUÀUÀ¼À MlÄÖ ¸ÀASÉå x EgÀ°.
|
ºÀAvÀ |
J°è |
JµÀÄÖ |
|
1 |
UÀĺÉUÉ |
{(x/5)-3}2 |
|
2 |
G½zÀzÀÄÝ |
1 |
{(x/5)-3}2+1 =x
(x2/25) –(6x/5)+9+1=x
(x2/25) –(11x/5)+10=0
x2–55x+250=0
(x-50)*(x-5) =0
x=50 CxÀªÁ x=5: 5 ¸ÁzsÀå«®è KPÀAzÀgÉ {(x/5)-3} IÄt DUÀ¨ÁgÀzÀÄ
vÁ¼É:
50=
(10-3)2+1= 49+1,
2.19.2 ªÀUÀð
¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼À ¸Àé¨sÁªÀ(Nature of roots of a
Quadratic equation)
¤ÃªÀÅ FªÀgÉUÉ ¸ÀªÀĸÉåUÀ¼À£ÀÄß ©r¸ÀĪÁUÀ b2-4ac AiÀÄ
¨É¯ÉUÀ¼À£ÀÄß UÀªÀĤ¹¢ÝÃgÁ?
2.19.1 .5gÀ°è b2-4ac
= 0 ªÀÄÆ®UÀ¼ÀÄ ¥ÀgÀ¸ÀàgÀ ¸ÀªÀÄ.
2.19.1 .8gÀ° b2-4ac
<0 ªÀÄÆ®UÀ¼ÀÄ CªÁ¸ÀÛ«PÀ ¸ÀASÉåUÀ¼ÀÄ.
G½zÀªÀÅUÀ¼À°è
b2-4ac
> 0 ªÀÄÆ®UÀ¼ÀÄ ªÁ¸ÀÛ«PÀ ¸ÀASÉåUÀ¼ÀÄ.
ªÀUÀð
¸À«ÄÃPÀgÀtUÀ¼À°è F b2-4acAiÀÄ£ÀÄß “±ÉÆÃzsÀ£À” (discriminant) J£ÀÄßvÉÛêÉ. EzÀ£ÀÄß 
(qɯÁÖ) ¢AzÀ
¸ÀÆa¸ÀÄvÉÛêÉ.
£Á«ÃUÀ F
wêÀiÁð£ÀPÉÌ §gÀÄvÉÛêÉ.
|
|
±ÉÆÃzsÀPÀzÀ ¨É¯É (b2-4ac)
= |
ªÀÄÆ®UÀ¼À ¸Àé¨sÁªÀ=[-b |
|
1 |
|
ªÀÄÆ®UÀ¼ÀÄ ªÁ¸ÀÛªÀ ªÀÄvÀÄÛ ¸ÀªÀÄ. |
|
2 |
|
ªÀÄÆ®UÀ¼ÀÄ ªÁ¸ÀÛªÀ¸ÀASÉåUÀ¼ÀÄ
ªÀÄvÀÄÛ ©ü£ÀߪÁVgÀÄvÀÛzÉ. |
|
3 |
|
ªÀÄÆ®UÀ¼ÀÄ ¸ÀªÀĪÀ®èzÀ CªÁ¸ÀÛ«PÀ ¸ÀASÉåUÀ¼ÀÄ (¸À«Ää±Àæ ¸ÀASÉåUÀ¼ÀÄ) |
2.19.2 ¸ÀªÀĸÉå 1: m£À AiÀiÁªÀ zsÀ£À ¨É¯ÉUÉ mk2-3k+1
=0 AiÀÄ ªÀÄÆ®UÀ¼ÀÄ (1) ¸ÀªÀÄ (2) ªÁ¸ÀÛªÀ ªÀÄvÀÄÛ ©ü£Àß (3)CªÁ¸ÀÛªÀ
ªÀÄvÀÄÛ ©ü£Àß?
¥ÀjºÁgÀ:
¸À«ÄÃPÀgÀt: mk2-3k+1
=0
E°è a=m, b= -3,
c= 1
b2-4ac
= 9 – 4m
1. ªÀÄÆ®UÀ¼ÀÄ ¸ÀªÀĪÁUÀ¨ÉÃPÁzÀgÉ,
b2-4ac
=0
(I.e. 9-4m =0, i.e. m =
9/4)
2. ªÀÄÆ®UÀ¼ÀÄ ªÁ¸ÀÛªÀ ªÀÄvÀÄÛ
©ü£ÀߪÁUÀ¨ÉÃPÁzÀgÉ, b2-4ac
>0
(I.e. 9-4m >0, i.e. 9 >4m, i.e. m < 9/4)
3. ªÀÄÆ®UÀ¼ÀÄ CªÁ¸ÀÛªÀ ªÀÄvÀÄÛ
©ü£ÀߪÁVgÀ¨ÉÃPÁzÀgÉ,
b2-4ac
<0
(I.e. 9-4m <0, i.e. 9 <4m, i.e. m > 9/4)
2.19.2 ¸ÀªÀĸÉå 2: m£À AiÀiÁªÀ
¨É¯ÉUÉ r2-(m+1)r +4 =0 ¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼ÀÄ
(¸ÀªÀÄ), (ªÁ¸ÀÛªÀ ªÀÄvÀÄÛ ©ü£Àß), (CªÁ¸ÀÛªÀ ªÀÄvÀÄÛ ©ü£Àß)
¥ÀjºÁgÀ:
¸À«ÄÃPÀgÀt: r2-(m+1)r
+4 =0
E°è a=1, b=
-(m+1), c= 4
b2-4ac
= (m+1) 2-16
= [(m+1)+4]*[(m+1)-4] ===> (C¥ÀªÀwð¹zÁUÀ)
= (m+5)(m-3)
1. ªÀÄÆ®UÀ¼ÀÄ ¸ÀªÀĪÁUÀ¨ÉÃPÁzÀgÉ,
b2-4ac =0
(i.e. (m+5)= 0 CxÀªÁ (m-3)=0
i.e. m=-5 CxÀªÁ m=3)
2. ªÀÄÆ®UÀ¼ÀÄ ªÁ¸ÀÛªÀ ªÀÄvÀÄÛ
©ü£ÀߪÁUÀ®Ä, b2-4ac >0
(i.e. (m+5)(m-3) >0) JgÀqÀÄ ¥ÀzÀUÀ¼À UÀÄt®§Þ
zsÀ£ÀªÁVzÀÝgÉ JgÀqÀÆ ¥ÀzÀUÀ¼ÀÄ zsÀ£ÀªÁVgÀ¨ÉÃPÀÄ E®è JgÀqÀÆ ¥ÀzÀUÀ¼ÀÄ
IÄtªÁVgÀ¨ÉÃPÀÄ J£ÀÄߪÀÅzÀ£ÀÄß UÀªÀĤ¹zÁUÀ,JgÀqÀÄ ¸ÀAzÀ¨sÀðUÀ¼ÀÄ ¸ÁzsÀå:
¸ÀAzÀ¨sÀð 1: m+5 >
0 ªÀÄvÀÄÛ m-3>0
I.e.
m> -5 ªÀÄvÀÄÛ m>3: »ÃVgÀ®Ä m>3 DVgÀ¯Éà ¨ÉÃPÀÄ
¸ÀAzÀ¨sÀð 2: m+5 <
0 ªÀÄvÀÄÛ m-3<0
I.e.
m< -5 ªÀÄvÀÄÛ m<3: »ÃVgÀ®Ä m<-5 DVgÀ¯Éà ¨ÉÃPÀÄ
3. ªÀÄÆ®UÀ¼ÀÄ CªÁ¸ÀÛªÀ ªÀÄvÀÄÛ
©ü£ÀߪÁUÀ®Ä, b2-4ac <0
(i.e. (m+5)(m-3) <0) JgÀqÀÄ ¥ÀzÀUÀ¼À UÀÄt®§Þ
IÄtªÁVzÀÝgÉ MAzÀÄ ¥ÀzÀ zsÀ£ÀªÁVzÀÄÝ E£ÉÆßAzÀÄ IÄtªÁVgÀ¨ÉÃPÀÄ J£ÀÄߪÀÅzÀ£ÀÄß
UÀªÀĤ¹zÁUÀ,JgÀqÀÄ ¸ÀAzÀ¨sÀðUÀ¼ÀÄ ¸ÁzsÀå:
¸ÀAzÀ¨sÀð 1: m+5 <
0 ªÀÄvÀÄÛ
m-3>0
I.e.
m< -5 ªÀÄvÀÄÛ m>3: EzÀÄ ¸ÁzsÀå«®è
¸ÀAzÀ¨sÀð 2: m+5 >
0 ªÀÄvÀÄÛ m-3<0
I.e.
m< -5 ªÀÄvÀÄÛ m<3: »ÃVgÀ®Ä m -5 ªÀÄvÀÄÛ 3 gÀ ªÀÄzsÀå EgÀ¯ÉèÉÃPÀÄ.
F jÃw £ÁªÀÅ PÀAqÀÄ
»r¢gÀĪÀÅzÀ£ÀÄß ¸ÀASÁågÉÃSÉAiÀÄ ªÉÄÃ¯É PɼÀUÉ PÁt¹zÀAvÉ UÀÄgÀÄw¸À§ºÀÄzÀÄ.
2.19.2 ¸ÀªÀĸÉå 3: (p+1) n2+2(p+3)n +(p+8) =0 F ¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼ÀÄ
¸ÀªÀĪÁUÀ¨ÉÃPÁzÀgÉ, pAiÀÄ ¨É¯É PÀAqÀÄ»r.
¥ÀjºÁgÀ:
zÀvÀÛ
¸À«ÄÃPÀgÀtªÀÅ ax2 +bx+ c =0 gÀÆ¥ÀzÀ°èzÉ.
a=(p+1), b= 2p+6, c= p+8
b2-4ac
= (2p+6)2
– 4*(p+1)(p+8)
= (4p2+24p+36) -4(p2+8p+p+8)
= 4p2+24p+36
-4p2-36p-32
=-12p+4
ªÀÄÆ®UÀ¼ÀÄ ¸ÀªÀĪÁUÀ¨ÉÃPÁzÀgÉ,
b2-4ac =0
I.e.
-12p+4 = 0
I.e. p=1/3
¸ÀÆvÀæzÀAvÉ, p=1/3 DzÁUÀ ªÀÄÆ®UÀ¼ÀÄ:
n = [-b ]/2a =[-2(p+3)0)
]/2(p+1) = - (p+3)/(p+1)
= - (10/3)/(4/3) = -5/2
vÁ¼É:
n = -5/2 £Àß
¸À«ÄÃPÀgÀtzÀ°è DzÉò¹,
(p+1) n2+2(p+3)n
+(p+8)
= 25(p+1)/4
-5(p+3) +(p+8)
=
25(p+1)/4 -4p -7
=
(25p+25-16p-28)/4
=
(9p-3)/4 (p = 1/3 DzÉò¹)
=0/4 = 0 = §®¨sÁUÀ
2.19.2 ¸ÀªÀĸÉå 4: (3p+1)c2+2(p+1)c+p=0
¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼ÀÄ ¸ÀªÀĪÁUÀ¨ÉÃPÁzÀgÉ. ‘p’AiÀÄ ¨É¯É PÀAqÀÄ»r.
¥ÀjºÁgÀ:
¸À«ÄÃPÀgÀtªÀÅ
ax2
+bx+ c =0
E°è a=(3p+1), b= 2p+2, c= p
b2-4ac
= (2p+2)2
– 4*(3p+1)p
= (4p2+4+8p) -4(3p2+p)
= 4p2+4+8p
-12p2-4p
= -8p2+4p+4
= - 4(2p2-p-1)
¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼ÀÄ
¸ÀªÀĪÁUÀ¨ÉÃPÁzÀgÉ, b2-4ac
=0
2p2-p-1
= 0
JqÀ§¢ = 2p2-2p+p-1
= 2p(p-1)+(p-1)
= (p-1)(2p+1)
FUÀ 2p2-p-1 = 0 DzÀÝjAzÀ (p-1)(2p+1)
= 0
p=1 CxÀªÁ
p= -1/2
UÀªÀĤ¹: 2p2-p-1
= 0 EzÀgÀ ªÀÄÆ®UÀ¼À£ÀÄß PÀAqÀÄ»rAiÀÄ®Ä C¥ÀªÀvÀð£À «zsÁ£À G¥ÀAiÉÆÃV¹zÉÝêÉ.
¸ÀÆvÀæzÀAvÉ p=1 DzÁUÀ, ªÀÄÆ®UÀ¼ÀÄ:
c = [-b +]/2a =[-2p-2 0) ]/2(3p+1) = -
4/8 = -1/2
p = -1/2 DzÁUÀ c UÉ E£ÉÆßAzÀÄ ¨É¯É (CzÉÃ)
§gÀÄvÀÛzÉ.
UÀªÀĤ¹: ¸ÀÆvÀæªÀ£ÀÄß JgÀqÀÄ ¨Áj
G¥ÀAiÉÆÃV¹AiÀÄÆ ªÉÄð£À ¸À«ÄÃPÀgÀtªÀ£ÀÄß ©r¹ ‘p’AiÀÄ ¨É¯É PÀAqÀÄ»rAiÀħºÀÄzÀÄ.
vÁ¼É:
¸À«ÄÃPÀgÀtzÀ°è c = -1/2 DzÉò¹zÁUÀ,
(3p+1) c2+2(p+1)c
+p
=
(3p+1)/4+2(p+1)(-1/2) +p
=(3p+1)/4
–(p+1) +p
=(3p+1)/4 -1
(4 £Àß ¸ÁªÀiÁ£Àå bÉÃzÀ ªÀiÁr)
= [(3p+1)
-4]/4 (p =1 DzÉò¹)
= 0/4 = 0 = zÀvÀÛ ¸À«ÄÃPÀgÀtzÀ §®§¢.
ZÀlĪÀnPÉ: p =
-1/2 DzÁUÀ, (3p+1) c2+2(p+1)c
+p =0 ¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼ÀÄ ¸ÀªÀĪÁVªÉAiÉÄà ¥ÀjÃQë¹.
2.19.2 ¸ÀªÀĸÉå 5: 2y2-py
+1 =0 ¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼ÀÄ ¸ÀªÀĪÁVzÀÝgÉ. ‘p’AiÀÄ ¨É¯É PÀAqÀÄ»r.
¥ÀjºÁgÀ:
zÀvÀÛ
¸À«ÄÃPÀgÀtªÀÅ ax2 +bx+ c =0 gÀÆ¥ÀzÀ°èzÉ.
E°è a=2, b= -p, c= 1
b2-4ac
= p2 -8
ªÀÄÆ®UÀ¼ÀÄ ¸ÀªÀĪÁVgÀ®Ä, b2-4ac
=0
p2 = 8 :
p = 2
ZÀlĪÀnPÉ: p AiÀÄ F ¨É¯ÉAiÀÄÄ ¸ÀªÀiÁ£À
ªÀÄÆ®UÀ¼À£ÀÄß PÉÆqÀÄvÀÛzÉAzÀÄ vÁ¼É£ÉÆÃr.
2.19.3 ªÀUÀð ¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ½UÀÆ, CªÀÅUÀ¼À
¸ÀºÁ¥ÀªÀvÀð£ÀUÀ½UÀÆ EgÀĪÀ ¸ÀA§AzsÀ(Relationship between roots and
co-efficients):
‘m’ ªÀÄvÀÄÛ ‘n’ UÀ¼ÀÄ
ªÀUÀð¸À«ÄÃPÀgÀt ax2 +bx+ c =0 EzÀgÀ ªÀÄÆ®UÀ¼ÁVgÀ°.
(x-m)(x-n) = 0
ªÀUÀð
¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼ÀÄ(m,n) :
x = [-b +]/2a CxÀªÁ x = [-b -]/2a
m = [-b +]/2a
n = [-b -]/2a
m+n = [-b +]/2a + [-b -]/2a
= -2b/2a = -b/a
mn = [-b +]/2a * [-b -]/2a (
(a+b)(a-b) ¸ÀÆvÀæ G¥ÀAiÉÆÃV¹zÉ)
= [ (-b)2-
{}2] /4a2
= [b2
-(b2-4ac) ] /4a2
= 4ac/4a2
= c/a
wêÀiÁð£À:
1) MAzÀÄ ªÀUÀð
¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼À ªÉÆvÀÛ = -b/a
2) MAzÀÄ ªÀUÀð
¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼À UÀÄt®§Þ = c/a
2.19.3 ¸ÀªÀĸÉå 1: x2 +(ab)x+ (a+b) =0 F
¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼À ªÉÆvÀÛ ªÀÄvÀÄÛ UÀÄt®§Þ PÀAqÀÄ»r.
¥ÀjºÁgÀ:
zÀvÀÛ
¸À«ÄÃPÀgÀtªÀÅ ax2 +bx+ c =0 gÀÆ¥ÀzÀ°èzÉ.
E°è a=1, b= ab, c= (a+b)
m+n = -b/a =
-ab/1 = -ab
mn =c/a
=(a+b)/1 = (a+b)
2.19.2 ¸ÀªÀĸÉå 2: pr2
= r-5 F ¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼À ªÉÆvÀÛ ªÀÄvÀÄÛ UÀÄt®§Þ PÀAqÀÄ»r.
¥ÀjºÁgÀ:
¸À«ÄÃPÀgÀt pr2
–r+5= 0
F ¸À«ÄÃPÀgÀtªÀÅ a x2
+bx+ c =0 gÀÆ¥ÀzÀ°èzÉ.
E°è a=p, b= -1, c= 5
m+n = -b/a =
1/p
mn =c/a = 5/p
2.19.4 zÀvÀÛ ªÀÄÆ®UÀ¼À£ÀÄß ºÉÆA¢gÀĪÀ ªÀUÀð
¸À«ÄÃPÀgÀtªÀ£ÀÄß gÀa¸ÀĪÀÅzÀÄ (Formation of equation with
given roots):
‘m’ ªÀÄvÀÄÛ ‘n’ UÀ¼ÀÄ ªÀUÀð
¸À«ÄÃPÀgÀt ax2 +bx+ c =0 EzÀgÀ ªÀÄÆ®UÀ¼ÁVgÀ°. DUÀ (x-m)(x-n) = 0
DzÀgÉ (x-m)(x-n)
=x(x-n)-m(x-n)
= x2 –xn –mx +mn
= x2 –x(n+m) +mn
= x2 –( m+n)x +mn
ªÀUÀð ¸À«ÄÃPÀgÀtzÀ ¸ÁªÀiÁ£Àå
gÀÆ¥À:-
x2 –(ªÀÄÆ®UÀ¼À
ªÉÆvÀÛ)x +(ªÀÄÆ®UÀ¼À UÀÄt®§Þ) =0
2.19.3 ¸ÀªÀĸÉå 1: 2a2-4a+1=0
F ¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼ÀÄ ‘p’ ªÀÄvÀÄÛ ‘q’ DzÀgÉ, (p+q)2+4pq
ªÀÄvÀÄÛ (p3 +q3)UÀ¼À ¨É¯É PÀAqÀÄ»r¬Äj ªÀÄvÀÄÛ p3 ªÀÄvÀÄÛ q3UÀ¼ÀÄ ªÀÄÆ®UÀ¼ÁUÀĪÀAvÉ
ªÀUÀð ¸À«ÄÃPÀgÀt §gÉ.
¥ÀjºÁgÀ:
zÀvÀÛ
¸À«ÄÃPÀgÀtªÀÅ ax2+bx+ c =0 gÀÆ¥ÀzÀ°èzÉ.
E°è a=2, b= -4, c= 1
p+q = -b/a =
4/2 =2
pq
=c/a =1/2
(p+q)2+4pq=4+2 = 6
£ÀªÀÄUÉ
MAzÀÄ ¸ÀÆvÀæ UÉÆwÛzÉ: a3+b3= (a+b) (a2+b2-ab)
p3
+q3
= (p+q)( p2+q2-pq)
= (p+q)[( p2+q2+2pq)
-3pq)]
= (p+q)[( p+q)2-3pq]
=2*[4-3/2] = 5 (
(p+q) ªÀÄvÀÄÛ pqUÀ¼À ¨É¯É DzÉò¹zÉ)
£ÀªÀÄVÃUÀ p3
ªÀÄvÀÄÛ q3UÀ¼ÀÄ ªÀÄÆ®UÀ¼ÁVgÀĪÀ ªÀUÀð
¸À«ÄÃPÀgÀt ¨ÉÃPÀÄ.
ªÀÄÆ®UÀ¼À ªÉÆvÀÛ = p3
+q3 =5 ( ªÉÄïÉ
¯ÉPÁÌZÁgÀ ªÀiÁrzÉ)
ªÀÄÆ®UÀ¼À UÀÄt®§Þ = p3*q3 = (pq)3 =(1/2)3 =1/8
¨ÉÃPÁzÀ
¸À«ÄÃPÀgÀt:
x2-(ªÀÄÆ®UÀ¼À ªÉÆvÀÛ)x+ (ªÀÄÆ®UÀ¼À
UÀÄt®§Þ)= 0
I.e. x2-5x+ 1/8= 0 (8 jAzÀ UÀÄt¹)
8x2-40x+1=0
2.19.3 ¸ÀªÀĸÉå 2: ªÀÄÆ®UÀ¼ÀÄ p/q ªÀÄvÀÄÛ q/p EgÀĪÀAvÉ
ªÀUÀð ¸À«ÄÃPÀgÀt gÀa¹.
¥ÀjºÁgÀ:
m =p/q, n=q/p
m+n =
p/q+q/p = (p2+q2)/pq
mn =
p/q*q/p =1
ªÀUÀð
¸À«ÄÃPÀgÀtzÀ DzÀ±Àð gÀÆ¥À: x2 –(n+m)x +mn= 0
I.e. x2 –(p2+q2)x/pq
+1 = 0
(pqx2
–(p2+q2)x +pq)/pq =0(pq ¸ÁªÀiÁ£Àå bÉÃzÀ ªÀiÁrzÉ)
I.e. pqx2 –(p2+q2)x
+pq=0
2.19.3 ¸ÀªÀĸÉå 3: x2+px+q=0
¸À«ÄÃPÀgÀtzÀ MAzÀÄ ªÀÄÆ®ªÀÅ ªÀÄvÉÆÛAzÀÄ ªÀÄÆ®zÀ ªÀÄÆgÀgÀ¶ÖÖzÀÝgÉ. 3p2=16q
JAzÀÄ ¸Á¢ü¹.
¥ÀjºÁgÀ:
zÀvÀÛ
¸À«ÄÃPÀgÀtªÀÅ ax2+bx+ c =0 gÀÆ¥ÀzÀ°èzÉ.
E°è a=1,b=p,c=q
m ªÀÄvÀÄÛ n UÀ¼ÀÄ ¸À«ÄÃPÀgÀtzÀ
ªÀÄÆ®UÀ¼ÁVgÀ°.
m+n = -b/a =
- p mn = c/a = q
MAzÀÄ ªÀÄÆ®ªÀÅ ªÀÄvÉÆÛAzÀgÀ 3 gÀ¶ÖzÉ m =3n DVgÀ°.
p = - (m+n) =-(3n+n)= -4n ªÀÄvÀÄÛ q =mn=3n*n = 3n2
3p2=
3(-4n)2= 48n2=16*3n2 = 16q(
3n2=q)
2.19.3 ¸ÀªÀĸÉå 4: 4x2-8px+9=0
¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼À £ÀqÀÄ«£À ªÀåvÁå¸À 4 DzÀgÉ ‘p’ AiÀÄ ¨É¯ÉAiÀÄ£ÀÄß PÀAqÀÄ»r¬Äj.
¥ÀjºÁgÀ:
zÀvÀÛ
¸À«ÄÃPÀgÀtªÀÅ ax2+bx+ c =0 gÀÆ¥ÀzÀ°èzÉ.
E°è a=4,b=-8p,c=9
m ªÀÄvÀÄÛ n UÀ¼ÀÄ ¸À«ÄÃPÀgÀtzÀ
ªÀÄÆ®UÀ¼ÁVgÀ°.
1) m+n
= -b/a = 8p/4 = 2p ===è(1)
2) mn=
c/a = 9/4 ===è(2)
ªÀÄÆ®UÀ¼À £ÀqÀÄ«£À ªÀåvÁå¸À 4 n = m+4 DVgÀ°.
n £À F ¨É¯ÉAiÀÄ£ÀÄß (1)gÀ°è DzÉò¹.
m+n = 2p
m+m+4 = 2p
2m= 2p-4
m=p-2 ------à(3)
n= m+4 EzÀ£ÀÄß (2) gÀ°è
DzÉò¹.
m(m+4) =9/4
m2+4m - 9/4 =0
I.e. (p-2)2+4(p-2) - 9/4 =0 {(3)gÀAvÉ m=p-2}
p2-4p+4 +4(p-2) - 9/4 =0 {(p-2)2 £ÀÄß
«¸ÀÛj¹zÁUÀ }
p2-4p+4 +4p-8 - 9/4 =0
p2-4 - 9/4 =0
p2-25/4 =0
p2= 25/4
p = 5/2
vÁ¼É:
p =(-5/2) ¨É¯ÉAiÀÄ£ÀÄß
zÀvÀÛ ¸À«ÄÃPÀgÀtzÀ°è DzÉò¹,
4x2-8px+9=0
4x2-8*(-5/2)x+9=0
4x2+20x+9=0
F ¸À«ÄÃPÀgÀtªÀÅ ax2+bx+c=0 gÀÆ¥ÀzÀ°èzÉ. a=4, b=20, c=9
b2-4ac
= 400 – 4*4*9 = 400-144 =256
= (256)
= 16
¸ÀÆvÀæzÀAvÉ,
ªÀÄÆ®UÀ¼ÀÄ: x = [-b +]/2a =(-20+16)/8
= -4/8
x
= [-b -]/2a = (-20-16)/8 = -36/8
ªÀÄÆ®UÀ¼À £ÀqÀÄ«£À ªÀåvÁå¸À 32/8 = 4 ¯ÉPÀÌzÀ°è PÉÆnÖzÉÝÃ.
ZÀlĪÀnPÉ: p=5/2 PÀÆqÁ EzÉÃ
¥sÀ°vÁA±À §gÀÄvÀÛzÉAzÀÄ vÁ¼É£ÉÆÃr.
2.19 PÀ°vÀ ªÀÄÄSÁåA±ÀUÀ¼ÀÄ
|
¸ÀASÉå |
£É£À¦qÀ¨ÉÃPÁzÀ CA±ÀUÀ¼ÀÄ |
|
1 |
ax2
+bx+ c = 0 F ªÀUÀð
¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼ÀÄ: x = [-b+ [-b- |
|
2 |
m ªÀÄvÀÄÛ nUÀ¼ÀÄ
MAzÀÄ ªÀUÀð ¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼ÁzÀgÉ, (m+n) = -b/a |
|
3 |
m ªÀÄvÀÄÛ n UÀ¼ÀÄ
MAzÀÄ ªÀUÀð ¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼ÁzÀgÉ, (mn) = c/a |
|
4 |
m ªÀÄvÀÄÛ n UÀ¼ÀÄ MAzÀÄ
ªÀUÀð ¸À«ÄÃPÀgÀtzÀ ªÀÄÆ®UÀ¼ÁzÀgÉ, x2 –(n+m)x +mn =0 |