3.3 UÀtUÀ¼ÀÄ - ¨sÁUÀ:2 (Sets- Part 2):

¦ÃpPÉ: PɼÀV£À ¸ÀªÀĸÉåAiÀÄ£ÀÄß UÀªÀĤ¹:

“MAzÀÄ vÀgÀUÀwAiÀÄ 60 «zÁåyðUÀ¼À°è ¥ÀæwAiÉƧâgÀÆ PÀ§rØ CxÀªÁ ºÁQ nÃA £À°è CxÀªÁ JgÀlÆ nÃA £À°è ¸ÉÃjPÉƼÀî ¨ÉÃPÀÄ. 45 ªÀÄA¢ PÀ§rØ nÃA ¸ÉÃjzÁÝgÉ ªÀÄvÀÄÛ 30 ªÀÄA¢ ºÁQ nÃA ¸ÉÃjzÁÝgÉ. ºÁUÁzÀgÉ JgÀqÀÆ nÃAUÀ¼À°è ¸ÉÃjPÉÆAqÀ «zÁåyðUÀ¼ÉµÀÄÖ”

UÀtUÀ¼À CzsÀåAiÀÄ£À EAvÀºÀ ¸ÀªÀĸÉåUÀ¼À£ÀÄß ©r¸À®Ä ¸ÀºÁAiÀÄPÁj.

3.3.1 UÀtUÀ¼À ®PÀëtUÀ¼ÀÄ (Properties of sets):

2+3 =3+2 , 2*3 =3*2.

¸ÀAPÀ®£À ªÀÄvÀÄÛ UÀÄuÁPÁgÀUÀ¼ÀÄ ¥ÀjªÀvÀð¤ÃAiÀÄ.

(2+3)+4= 2+(3+4) ; (2*3)*4= 2*(3*4).

¸ÀAPÀ®£À ªÀÄvÀÄÛ UÀÄuÁPÁgÀUÀ¼ÀÄ ¸ÀºÀªÀvÀð¤ÃAiÀĪÁVªÉ.

FUÀ £ÁªÀÅ UÀtUÀ¼À ®PÀëtUÀ¼À£ÀÄß w½AiÀÄĪÁ.

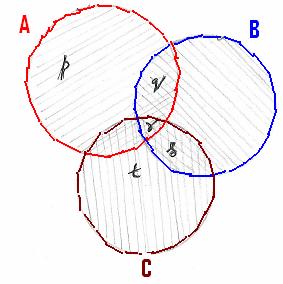
3.3.1 GzÁ 1 : UÀtUÀ¼ÀÄ: A = {p,q,r,} ,B = {q,r,s,} ªÀÄvÀÄÛ C={r,s,t} DzÀgÉ F PɼÀV£ÀªÀÅUÀ¼À£ÀÄß ¸Á¢ü¹:

1. BC =CB

2. BC = CB

3. A(BC) = (AB)C

4. A(BC) = (AB) C

5. A (BC) = (AB) (AC)

6. A (BC) = (AB)(AC)

7.

¥ÀjºÁgÀ:

BC = {q,r,s}{r,s,t} = {q,r,s,t} ------à(1) CB = {r,s,t} {q,r,s} ={q,r,s,t} -------à(2) (1) ªÀÄvÀÄÛ (2) jAzÀ, BC =CB 1. UÀtUÀ¼À ¸ÀAAiÉÆÃUÀªÀÅ ¥ÀjªÀvÀð¤ÃAiÀĪÁVzÉ.(Union of sets is commutative): BC = {q,r,s}{r,s,t} = {r,s} -----à(3) CB = {r,s,t} {q,r,s} = {r,s} -----à(4) (3) ªÀÄvÀÄÛ (4) jAzÀ, BC = CB 2. UÀtUÀ¼À bÉÃzÀ£ÀªÀÅ ¥ÀjªÀvÀð¤ÃAiÀĪÁVzÉ.(Intersection of sets is commutative): AB = {p,q,r,}{q,r,s} = {p,q,r,s} A(BC) = {p,q,r} {q,r,s,t} ={p,q,r,s,t,} ---à(5) (AB)C= {p,q,r.s}{r,s,t} = {p,q,r,s,t} ---------à(6) (5) ªÀÄvÀÄÛ (6) jAzÀ, A(BC) = (AB)C 3. UÀtUÀ¼À ¸ÀAAiÉÆÃUÀªÀÅ ¸ÀºÀªÀvÀð¤ÃAiÀĪÁVzÉ. (Union of sets is associative): AB = {p,q,r}{q,r,s} = {q,r} A (BC) ={p,q,r}{r,s} ={r} ------à(7) (AB) C = {q,r}{r,s,t} = {r} ------à(8) (7) ªÀÄvÀÄÛ (8) jAzÀ, A(BC) = (AB) C 4. UÀtUÀ¼À bÉÃzÀ£ÀªÀÅ ¸ÀºÀªÀvÀð¤ÃAiÀĪÁVzÉ.(Intersection of sets is associative): A (BC) = {p,q,r}{r,s} = {p,q,r,s} -----------------à(9) AC = {p,q,r}{r,s,t} = {p,q,r,s,t} (AB) (AC) = {p,q,r,s}{p,q,r,s,t} ={p,q,r,s} ----à(10) (9) ªÀÄvÀÄÛ (10) jAzÀ, A (BC) = (AB) (AC) 5.UÀtUÀ¼À ¸ÀAAiÉÆÃUÀªÀÅ bÉÃzÀ£ÀzÀ ªÉÄÃ¯É «¨sÁdPÀvÉAiÀÄ£ÀÄß ºÉÆA¢zÉ.(Union of sets is distributive over intersection of sets): A (BC) = {p,q,r,}{q,r,s,t} ={q,r} ----à(11) (AB) = {p,q,r}{q,r,s} = {q,r} (AC) = {p,q,r}{r,s,t} = {r} (AB)(AC)= {q,r}{r} = {q,r} --------à(12) (11) ªÀÄvÀÄÛ (12) jAzÀ, A (BC) = (AB)(AC) 6.UÀtUÀ¼À bÉÃzÀ£ÀªÀÅ ¸ÀAAiÉÆÃUÀzÀ ªÉÄÃ¯É «¨sÁdPÀvÉAiÀÄ£ÀÄß ºÉÆA¢zÉ.(Intersection of sets is distributive over union of sets):

r’ ªÀiÁUÀð£ÀߣÀ ¤AiÀĪÀÄUÀ¼ÀÄ(De Morgan’s laws):-

¸Á¢ü¹:

1. (AB)¹= A¹B¹ (JgÀqÀÄ UÀtUÀ¼À ¸ÀAAiÉÆÃUÀ UÀtzÀ ¥ÀÇgÀPÀUÀtªÀÅ D JgÀqÀÄ UÀtUÀ¼À ¥ÀÇgÀPÀ UÀtUÀ¼À bÉÃzÀ£ÀPÉÌ ¸ÀªÀÄ)

(The complement of union of sets is the intersection of their complements)

2. (AB)¹= A¹B¹(JgÀqÀÄ UÀtUÀ¼À bÉÃzÀ£À UÀtzÀ ¥ÀÇgÀPÀ UÀtªÀÅ D JgÀqÀÄ UÀtUÀ¼À ¥ÀÇgÀPÀ UÀtUÀ¼À ¸ÀAAiÉÆÃUÀPÉÌ ¸ÀªÀÄ)

(The complement of the intersection of sets is the union of their complements)

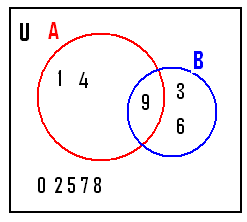
3.3.1 GzÁ2 : U = {0,1,2,3,4,5,6,7,8,9} -- (10QÌAvÀ PɼÀV£À ¸ÀASÉåUÀ¼ÀÄ)A = {x:10QÌAvÀ PɼÀV£À ¥ÀÇtðªÀUÀð ¸ÀASÉå} B = {x:10QÌAvÀ PɼÀV£À 3 gÀ C¥ÀªÀvÀåðUÀ¼ÀÄ}

FUÀ £ÁªÀÅ A ªÀÄvÀÄÛ B UÀtzÀ UÀuÁA±ÀUÀ¼À£ÀÄß §gÉAiÀÄĪÁ. A = {1,4,9} (G½zÀ CA±ÀUÀ¼ÀÄ ¥ÀÇtðªÀUÀðUÀ¼À®è) B = {3,6,9} (3 = 3*1, 6=3*2,9=3*3) A^1= U-A (AAiÀÄ°è E®èzÀ U zÀ°è G½zÀ UÀuÁA±ÀUÀ¼À UÀtªÉà A^1) = {0,1,2,3,4,5,6,7,8,9} - {1,4,9} ={0,2,3,5,6,7,8} =========à(1) B^1= U-B (B AiÀÄ°è E®èzÀ U zÀ°è G½zÀ UÀuÁA±ÀUÀ¼À UÀtªÉà B^1) ={0,1,2,3,4,5,6,7,8,9} - {3,6,9} ={0,1,2,4,5,7,8} =========à(2) (1) ªÀÄvÀÄÛ (2) jAzÀ, A^1B^1= {0,2,3,5,6.7,8}{0,1,2,4,5,7,8} ={0,2,5,7,8} ==================à(3) (AB) = {1,4,9}{3,6,9} = {1,3,4,6,9} (AB)^1= U -(AB) = {0,1,2,3,4,5,6,7,8,9}- {1,3,4,6,9} = {0,2,5,7,8} ==à(4) (3) ªÀÄvÀÄÛ (4) jAzÀ, 1. (AB)^1= A^1B^1 (1) ªÀÄvÀÄÛ (2) jAzÀ A^1B^1= {0,2,3,5,6,7,8}{0,1,2,4,5,7,8} ={0,1,2,3,4,5,6,7,8}==============à(5) AB = {1,4,9}{3,6,9}= {9} (AB)^1= U – (AB) = {0,1,2,3,4,5,6,7,8,9}- {9} ={0,1,2,3,4,5,6,7,8} =======à(6) (5) ªÀÄvÀÄÛ (6)jAzÀ, 2. (AB)^1= A^1B^1

3.3.2 JgÀqÀÄ UÀtUÀ¼À°è£À UÀuÁA±ÀUÀ¼À ¸ÀASÉåUÀ¼À £ÀqÀÄ«£À ¸ÀA§AzsÀ

(Relationship between numbers of elements of 2 sets)

A UÀtzÀ°è£À UÀuÁA±ÀUÀ¼À ¸ÀASÉåAiÀÄ£ÀÄß n(A) JAzÀÄ §gÉAiÀÄÄvÉÛêÉ.(‘cardinal number’ )

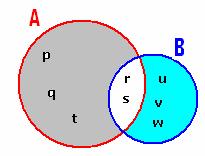
3.3.2 GzÁ1 : A= {p,q,r,s,t} ªÀÄvÀÄÛ B= {r,s,u,v,w} DVgÀ°.

n(A) =n(B)=5 AB ={p,q,r,s,t}{r,s,u,v,w}= {p,q,r,s,t,u,v,w} AB ={p,q,r,s,t}{r,s,u,v,w} =(r,s} n(AB) =8, n(AB) =2 n(A) +n(B) = 5+5 =8+2 = n(AB) +n(AB) F ¸À«ÄÃPÀgÀtªÀ£ÀÄß E£ÀÄß ¸ÀàµÀÖªÁV »ÃUÉ §gÉAiÀħºÀÄzÀÄ: 1. n(AB)= n(A) +n(B)-n(AB) 2. n(AB)= n(A) +n(B)-n(AB) 3. A ªÀÄvÀÄÛ B UÀ¼ÀÄ ºÉÆAzÁtÂPɬĮèzÀ UÀtUÀ¼ÁzÀgÉ, n(AB)= n(A) +n(B) ( n(AB)=0 KPÉAzÀgÉ AB = { }=(A ªÀÄvÀÄÛ B UÀ¼ÀÄ ºÉÆAzÁtÂPɬĮèzÀ UÀtUÀ¼ÀÄ).

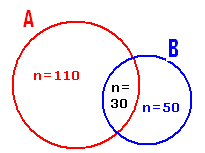
3.3.2 ¸ÀªÀĸÉå1: M§â ºÀƪÀiÁgÀĪÀªÀ£À §½ PÉ®ªÀÅ ºÁgÀUÀ½ªÉ. 110 ºÁgÀUÀ¼ÀÄ ¸ÀA¦UÉ ºÀƪÀÅUÀ½AzÀ PÀÆrzÉ, 50 ºÁgÀUÀ¼ÀÄ ªÀÄ°èUÉ ºÀƪÀÅUÀ½zÀ PÀÆrzÉ. ªÀÄvÀÄÛ 30 ºÁgÀUÀ¼ÀÄ JgÀqÀÆ §UÉAiÀÄ ºÀƪÀÅUÀ¼À£ÀÄß ºÉÆA¢zÉ. ºÁUÁzÀgÉ CªÀ£À §½ EgÀĪÀ ºÁgÀUÀ¼À ¸ÀASÉå JµÀÄÖ?

¥ÀjºÁgÀ:

A AiÀÄÄ ¸ÀA¦UÉ ºÀÆUÀ½AzÀ PÀÆrzÀ ºÁgÀUÀ¼À UÀtªÁVgÀ°. n(A) =110. B AiÀÄÄ ªÀÄ°èUÉ ºÀÆUÀ½AzÀ PÀÆrzÀ ºÁgÀUÀ¼À UÀtªÁVgÀ°. n(B)= 50. AB AiÀÄÄ JgÀqÀÆ §UÉAiÀÄ ºÀÆUÀ½AzÀ PÀÆrzÀ ºÁgÀUÀ¼À UÀt. n(AB)=30. AB AiÀÄÄ K¯Áè ºÁgÀUÀ¼À UÀt. n(AB)= n(A) +n(B)-n(AB) = 110+50-30 =130 ºÀƪÀiÁgÀĪÀªÀ£À §½ 130 ºÁgÀUÀ½ªÉ.

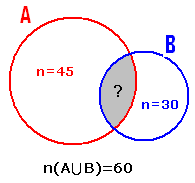
3.3.2 ¸ÀªÀĸÉå 2: MAzÀÄ vÀgÀUÀwAiÀÄ 60 «zÁåyðUÀ¼À°è ¥ÀæwAiÉƧâgÀÆ PÀ§rØ CxÀªÁ ºÁQ nÃA £À°è CxÀªÁ JgÀlÆ nÃA £À°è ¸ÉÃjPÉƼÀî ¨ÉÃPÀÄ. 45 ªÀÄA¢ PÀ§rØ nÃA ¸ÉÃjzÁÝgÉ ªÀÄvÀÄÛ 30 ªÀÄA¢ ºÁQ nÃA ¸ÉÃjzÁÝgÉ. ºÁUÁzÀgÉ JgÀqÀÆ nÃAUÀ¼À°è ¸ÉÃjPÉÆAqÀ «zÁåyðUÀ¼ÉµÀÄÖ?( 3.1 ¦ÃpPÉ AiÀÄ°è £À ¸ÀªÀĸÉå)

¥ÀjºÁgÀ:

A AiÀÄÄ PÀ§rØ nÃA «zÁåyðUÀ¼À UÀtªÁVgÀ°. n(A) =45 B AiÀÄÄ ºÁQ nÃA «zÁåyðUÀ¼À UÀtªÁVgÀ°. n(B) = 30 AB AiÀÄÄ JgÀqÀÆ nÃAUÀ¼À°è£À «zÁåyðUÀ¼À UÀtªÁVgÀ°. n(AB)- PÀAqÀÄ»rAiÀĨÉÃPÁzÀzÀÄÝ. AB AiÀÄÄ vÀgÀUÀwAiÀÄ°è£À «zÁåyðUÀ¼À UÀt. n(AB)=60 - zÀvÀÛ n(AB)= n(A) +n(B)-n(AB) n(AB)= n(A) +n(B)- n(AB) = 45+30-60 =15 15 «zÁåyðUÀ¼ÀÄ JgÀqÀÆ nÃAUÀ¼À°è DAiÉÄÌ EzÁÝgÉ.

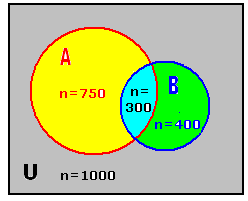
3.3.2 ¸ÀªÀĸÉå 3 :MAzÀÄ ¸Á«gÀ PÀÄlÄA§UÀ¼À£ÀÄß ¸ÀAzÀ²ð¸À¯ÁV, 750 PÀÄlÄA§UÀ¼ÀÄ ªÁvÁðZÁ£É¯ï£ÀÆß 400 PÀÄlÄA§UÀ¼ÀÄ QæÃqÁ ZÁ£É¯ï£ÀÆß ªÀÄvÀÄÛ 300 PÀÄlÄA§UÀ¼ÀÄ JgÀqÀÆ ZÁ£É¯ïUÀ¼À£ÀÆß «ÃQë¸ÀĪÀÅzÀÄ PÀAqÀħAvÀÄ.

ºÁUÁzÀgÉ.

1. JµÀÄÖ PÀÄlÄA§UÀ¼ÀÄ ªÁvÁðZÁ£É¯ï ªÀiÁvÀæ «ÃQë¸ÀÄvÁÛgÉ?

2. JµÀÄÖ PÀÄlÄA§UÀ¼ÀÄ QæÃqÁ ZÁ£É¯ï ªÀiÁvÀæ «ÃQë¸ÀÄvÁÛgÉ?

3. JµÀÄÖ PÀÄlÄA§UÀ¼ÀÄ n°«µÀ£ï «ÃQë¸ÀĪÀÅ¢®è?

¥ÀjºÁgÀ:

¸ÀAzÀ²ð¹zÀ PÀÄlÄA§UÀ¼À UÀt: U DVgÀ°. n (U) =1000 ªÁvÁðZÁ£É¯ï £ÉÆÃqÀĪÀªÀgÀ PÀÄlÄA§UÀ¼À UÀt: A DVgÀ°. n (A) =750 QæÃqÁ ZÁ£É¯ï £ÉÆÃqÀĪÀªÀgÀ PÀÄlÄA§UÀ¼À UÀt : B DVgÀ°. n(B)=400 JgÀqÀÆ ZÁ£É¯ï £ÉÆÃqÀĪÀªÀgÀ PÀÄlÄA§UÀ¼À UÀt: AB n(AB)=300 UÀªÀĤ¹: 1. A-AB ªÁvÁðZÁ£É¯ï ªÀiÁvÀæ £ÉÆÃqÀĪÀªÀgÀ UÀt. C°ègÀĪÀ UÀuÁA±ÀUÀ¼À ¸ÀASÉå = n [A-AB]. 2. B- AB QæÃqÁ ZÁ£É¯ï ªÀiÁvÀæ £ÉÆÃqÀĪÀªÀgÀ UÀt. C°ègÀĪÀ UÀuÁA±ÀUÀ¼À ¸ÀASÉå = n [B-AB]. 3. AB AiÀÄÄ n°«µÀ£ï £ÉÆÃqÀĪÀªÀgÀ UÀt. n(AB)= n(A)+n(B)-n(AB) = 750+400-300 = 850 4. (AB)^1 mÉ°«µÀ£ÀߣÀ £ÉÆÃqÀzÉà EgÀĪÀªÀgÀ UÀt. C°ègÀĪÀ UÀuÁA±ÀUÀ¼À ¸ÀASÉå = n(AB)^1 FUÀ, 1. n [A-AB] = n(A) – n(AB) = 750 -300 = 450 2. n [B-AB] = n(B) – n(AB) = 400 -300 = 100 3. n(AB)^1= n[U – (AB)] = n(U) – n((AB)) = 1000-850 = 150

3.3 PÀ°vÀ ªÀÄÄSÁåA±ÀUÀ¼ÀÄ

PÀæ.¸ÀA.	£É£À¦qÀ¨ÉÃPÁzÀ CA±ÀUÀ¼ÀÄ
1	(AB)^1= A^1B^1
2	(AB)^1= A^1B^1
3	n(AB)= n(A) +n(B)-n(AB)
4	n(AB)= n(A) +n(B)-n(AB)