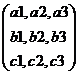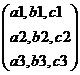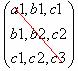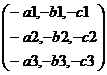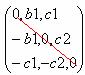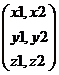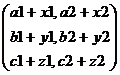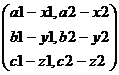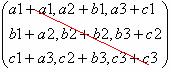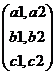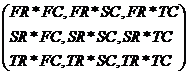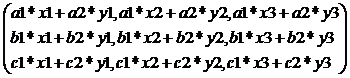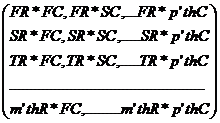3.6 Matrix operations:
1)
Multiplication of a matrix by a constant:
|
A = |
k |
Multiply each element of matrix by the constant k k(A) = (k*A’s all elements) |
2)
Equality of 2 Matrices
|
A = |
B = |
If (A) =(B) then (x1=z1 , x2=z2 , x3=z3) , (y1=t1 , y2=t2 ,
y3=t3). Two matrices are ‘equal’
if their corresponding elements are equal |
1) if A = A1 then
A is a symmetric matrix
Proof
|
A = |
A1
= |
If,A =A1
then a2=b1, a3=c1, b3=c2 |
A = |
Thus A
is a symmetric matrix ( |
2)
if A = - A1 then A is a skew symmetric
matrix
Proof
|
A = |
- A1
= |
If A
=-A1 then a1=
-a1,a2= -b1, a3=-c1, b1=-a2,b2=
-b2, b3= -c2, c1
= -a3,c2= -b3,c3=-c3
|
A = |
Thus A
is both symmetric and skew. ( |
3.6.1 Addition &
Subtraction of Matrices:
1. If A and B are two matrices of the same order then their sum
(A+B) is the matrix obtained by adding the corresponding elements of A with the
elements of B.
2. If A and B
are two matrices of the same order then their difference (A-B) is the matrix
obtained by subtracting the corresponding elements of B from the elements of A.
|
A = |
B = |
A+B = |
a1+x1=x1+a1 |
||
|
Since addition of numbers is commutative, addition of matrices
is also commutative. Thus A+B=B+A |
|||||
|
A = |
B = |
A-B = |
a1-x1 |
||
|
Since subtraction of numbers is not commutative, subtraction
of matrices is also not commutative. Thus A-B |
|||||
|
We notice that for addition and subtraction matrices need to be of same order. |
|||||
|
A = |
A1
= |
A+ A1
= |
This is a symmetric matrix ( |
||
|
A = |
A1
= |
A- A1
= |
This is a skew matrix as elements across the principal diagonal are zero. |
||
3.6.2 Multiplication of
matrices:
|
A = |
B = |
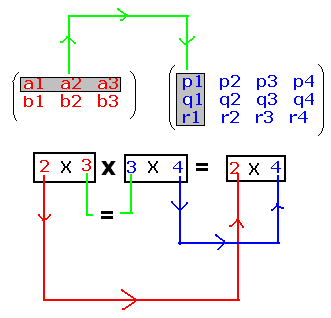
Elements
in Rows of A are (a1,a2),
(b1,b2) and (c1,c2). Elements
in Columns of B are (x1,y1),
(x2,y2) and(x3,y3) |
Let us define multiplication operation of 2 pairs of
elements [(a1,a2) What
did we do? We multiplied row elements s of A with corresponding column
elements of B. |
||||||||||||||||||||
|
Let us
use the following abbreviations. FR(First row of
A) FC(First column of B) SR (Second row of
A) SC(Second Column of B) TR (Third row of
A) TC(Third Column of B) We define Multiplication of Matrices as follows:
AB = Note :
A is a 3x2 matrix and B is a 2x3 matrix. AB became a 3 x 3 matrix. |
|||||||||||||||||||||||
A =  , C =
, C = (3 x 3).
(3 x 3).
Can we multiply A with C?
A’s row values (a1, a2) which are 2 in number, can not be matched with C’s
column values (x1,y1,z1) which are 3 in number.
Generalization : For matrix multiplication, we multiply each
column values of each row of one matrix (A) with each row values of another
matrix (B)for every column of B.
Hence these two numbers
should be equal (Number of columns of A = Number of rows of B)
Because of this reason AC
is not possible.
General
Method:
|
A= |
B= |
FR(First row of A) SR (Second row of A) TR (Third row of A) …………………… m’thR(m’th row of A) FC(First column of B) SC(Second Column B) ……………………… P’th(p’th Column of B) |
AB = |
|
If A is a matrix of order m x n and B is a matrix of
order n x p then AB is a matrix of order m x p. |
|
||
If A = 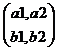 , B =
, B = ![]() ,C=
,C= ![]() , I=
, I= ![]()
Exercise :
Prove the following which is also true for any matrices.
|
No. |
Operation |
Property |
|
1 |
(AB)1=
B1 A1 |
|
|
2 |
AI=IA=A |
This is
true for any Square matrix. |
|
3 |
A+B
=B+A |
Commutative
Property |
|
4 |
A-B |
|
|
5 |
AB |
|
|
4 |
A(BC)
=(AB)C |
Associative
Property |
|
5 |
A(B+C)=AB+AC |
Distributive
property w.r.t addition |
|
6 |
A(B-C)
=AB-AC |
Distributive
property w.r.t subtraction |
3.6.2 Problem 1:
If A = ![]() and B =
and B = ![]() show that AB
show that AB![]() BA
BA
Solution
:
AB = ![]()
BA = ![]()
The matrices AB and BA are
not same
3.6.2 Problem 2: IF A=
![]() and B=
and B=![]() verify that (A+B)1
= A1+B1
verify that (A+B)1
= A1+B1
Solution
:
A+B =![]() (A+B)1 =
(A+B)1 =![]()
A1=![]() B1=
B1=![]() A1+B1=
A1+B1=
![]()
3.6.2 Problem 3: If A= ![]() show that A2-8A+13I
=0
show that A2-8A+13I
=0
Solution
:
A2= A*A = ![]() =
= ![]()
-8A = ![]()
13I = ![]() =
= ![]()
A2-8A+13I = ![]() =
= ![]()
3.6.2 Problem 4: Find x and y given ![]()
![]() =
= ![]()
![]()
Solution
:
Multiplication of two
matrices gives us
LHS = ![]()
RHS = ![]() =
= ![]()
So we have
x+3y = -7 --à(1)
5x-2y = -1 --à(2)
5x+15y = -35 ---à(3) (Multiply (1) by 5)
-17y =34 ( Subtract (3)
from (2))
![]() y = -2
By substituting this value in (1) we
get
y = -2
By substituting this value in (1) we
get
x-6 = -7
![]() x = -1
x = -1
Verfication:
Verify the equality of
product of matrices by substituting values of x and y.
Application of Matrix Theory:
Let us work with a real
life problem for solution using theory of matrix.
3.6.2 Problem 5: The 11 railway connections
between cities of Karnataka, Maharashtra and
|
No |
Starting
place |
Destination |
|
1 |
Mangaluru |
Mumbai |
|
2 |
Mangaluru |
Pune |
|
3 |
Hubballi |
Pune |
|
4 |
Belagavi |
Nagapura |
|
5 |
Mumbai |
|
|
6 |
Mumbai |
|
|
7 |
Pune |
|
|
8 |
Pune |
|
|
9 |
Pune |
Vadodara |
|
10 |
Nagapura |
|
|
11 |
Nagapura |
Vadodara |
Solution
:
For easy understanding let
us represent the problem in a diagram:
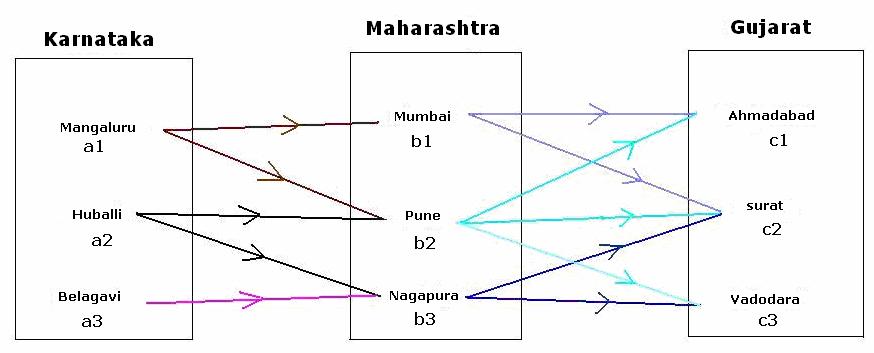
If cities are represented
in alphabets as above then
|
Routes
from Karnataka to |
Equivalent Matrix |
Routes
from Maharashtra to |
Equivalent Matrix |
Product
of matrices |
Equivalent
Matrix |
||||||||||||||||||||||||||||||||||||||||||||||||
|
P = |
|
Q = |
PQ = |
|
Thus
we conclude that, there are 2
direct routes from Mangaluru
to
3.6. Summary of learning
|
No. |
Points learnt |
|
1 |
(AB)1=
B1 A1 |
|
2 |
AI=IA=A |
|
3 |
A+B
=B+A |
|
4 |
A-B |
|
5 |
AB |
|
4 |
A(BC) =(AB)C |
|
5 |
A(B+C)=AB+AC |
|
6 |
A(B-C)
=AB-AC |
Additional Points:
Note the following
properties by taking suitable matrices.
1. If A ![]() 0 and AB=AC then it is
not necessary that B=C
0 and AB=AC then it is
not necessary that B=C
2. If AB = 0 then it is not necessary that A=0
or B=0
3. If A=0 or B=0 then AB = 0 = BA
4. (A+B)(A-B) ![]() A2-B2
A2-B2
3.6.2 Problem 4: Find matrix M such that M ![]() =
= ![]()
Solution:
First we need to find the
order of matrix M
Note the order of matrix ![]() is 2 by 2
is 2 by 2
Since the product of
matrices is 1 by 2
M has to be a 1 by 2 matrix
so that
(1 by 2 Matrix)*(2 by 2 Matrix) = (1 by 2 Matrix)
Let M = ![]() , On multiplying the two matrices we get
, On multiplying the two matrices we get
![]()
![]() =
= ![]()
Since it is given that the
product of M and the given matrix is equal to![]()
It follows that x = 1 and
x+2y = 2
On Solving, we get x = 1
and y = 1/2.
![]() Matrix M =
Matrix M = ![]()
Verification:
Verify that ![]()
![]() =
=![]()
3.6.3 Determinants:
Let A =  be a 2 x 2 square matrix. We define the ‘determinant’ of A denoted by |A| as a real
number |A|= ad-bc.
be a 2 x 2 square matrix. We define the ‘determinant’ of A denoted by |A| as a real
number |A|= ad-bc.
A square matrix is called ‘singular matrix’ if its determinant is zero.
A square matrix is called ‘non-singular matrix’ if its determinant is not
zero.
For a given matrix A, its inverse A-1 is defined as a matrix such
that AA-1 = I (identity matrix)
Let us find the properties
of A-1
Then AA-1 = 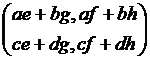
Since by definition AA-1=![]() , it follows that we need to have
, it follows that we need to have
ae+bg = 1, af+bh = 0, ce+dg
= 0 and cf+dh = 1.
By expressing e, f, g and h
in terms of a, b, c and d we get
e = d/(ad-bc), f = -b/(ad-bc), g = -c/(ad-bc), h = a/(ad-bc)
Thus
A-1 = 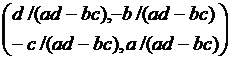 =
= ![]()
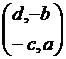
Note that ad-bc = |A|
Thus if |A| = 0, then A-1
does not exist.
Hence, a singular matrix
does not have its inverse.
Also note that | A-1|
= (ad-bc)
3.6.3 Problem 1: Find the inverse of A=![]() and also its determinant
and also its determinant
Solution:
Here |A| = (2*-3-0*5) = -6
Since |A| ![]() 0 A-1 exists
0 A-1 exists
A-1 = -1/6![]() =
= ![]()
|A-1|= -1/6
Also note |AA-1|=
(-6)(-1/6) = 1
3.6.4
Solving of simultaneous linear equations
We have learnt to solve
simultaneous linear equations by algebraic method and by graphical method.
Now we will learn two more
methods using matrix theory.
3.6.4.1 Inverse Matrix method
Let ax+by = p and cx+dy = q
be two linear equations
Let A = a 2 by 2 matrix, X=
a 2 by 2 matrix, X= ![]() a 2 by 1 matrix and P
=
a 2 by 1 matrix and P
= ![]() a 2 by 1 matrix.
a 2 by 1 matrix.
Hence AX = 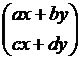 which is =
which is = ![]() = P
= P
Thus in matrix form AX = P.
Let us multiply both sides by A-1 (It exists when ad-bc ![]() 0)
0)
AA-1X = A-1P
i.e. IX = A-1P
(since IX = X) we have,
X = ![]() =
= ![]()
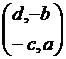
![]() =
= ![]()
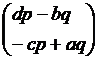 (By matrix
multiplication)
(By matrix
multiplication)
Thus x = (dp-bq)/(ad-bc)
and y = (aq-pc)/(ad-bc).
3.6.4 Problem 1: Solve 2x-3y+6 = 0 and 6x+y+8 = 0
using matrix inversion method.
Solution:
The given equations are
rewritten as:
2x-3y = -6 and
6x+y = -8
So we have
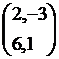
![]() =
=![]()
Let A = 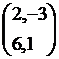 , then |A| = 2-(-3*6) = 20. Since |A|
, then |A| = 2-(-3*6) = 20. Since |A|![]() 0, A-1 exists and
0, A-1 exists and
A-1 = 1/20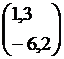 =
= 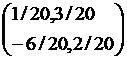
Since X = A-1P
X = ![]() =
= 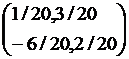
![]() =
= 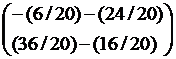 =
= 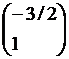
Thus x = -3/2
and y = 1
3.6.4.2. Cramer’s method
As in 3.6.4.1 let ax+by = p
and cx+dy = q be two linear equations. Let A, X and P be matrices as defined in
3.6.4.1.
Hence AX = 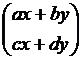 which is =
which is =![]() = P
= P
Thus in matrix form AX= P
and we note |A| = ad-bc.
Let P2A= 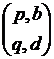 and A1P=
and A1P=  be two other matrices formed by elements of matrices A and P.
be two other matrices formed by elements of matrices A and P.
Then x = |P2A|/|A|
= (pd-bq)/(ad-bc) and y = |A1P|/|A|=(aq-cp)/(ad-bc).
3.6.4 Problem 2: Solve the problem 3.6.4 Problem 1
using Cramer’s method.
Solution:
The given equations are
rewritten as:
2x-3y = -6 and
6x+y = -8
So we have
A= 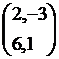 , X=
, X=![]() and P =
and P =![]()
![]() |A| = 2+18=20
|A| = 2+18=20
Then P2A=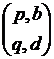 =
=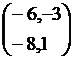 and A1P=
and A1P= 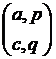 =
= 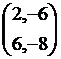
![]() |A| = 2+18=20, |P2A| = -6-24 = -30
, |A1P| = -16+36 = 20
|A| = 2+18=20, |P2A| = -6-24 = -30
, |A1P| = -16+36 = 20
x = (-30/20) = -3/2 and y =
20/20 = 1
These are the
same solutions that we got in problem 3.6.4 Problem 1.