3.7 ಮಾಡ್ಯುಲೋ ಗಣಿತ (Modular Arithmetic):

3.7.1 ಪೀಠಿಕೆ:

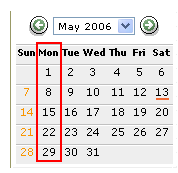
ಬಲಭಾಗದಲ್ಲಿರುವ ಮೇ 2006 ರ ಕ್ಯಾಲೆಂಡರ್ ಗಮನಿಸಿ. 1 ನೇ ತಾರೀಕು ಸೋಮವಾರ ಬಂದಿದೆ.ಹಾಗಾದರೆ 29ನೇ ತಾರೀಕು ಯಾವ ವಾರ?ಅದು ಪುನಃ ಸೋಮವಾರ. ಇದನ್ನು ಹೇಗೆ ಗ್ರಹಿಸಬಹುದು? 1 ನೇ ತಾರೀಕು ಸೋಮವಾರವಾದರೆ ಮುಂದಿನ ಸೋಮವಾರಗಳ ತಾರೀಕು: 1,8 (1+7),15(8+7),22(15+7),29(22+7) ಇದು ಹೇಗೆ? ಏಕೆಂದರೆ ವಾರದಲ್ಲಿ 7 ದಿನಗಳಿವೆ. ಆದ್ದರಿಂದ ಯಾವುದೇ ದಿನವು ಒಂದು ವಾರದಲ್ಲಿ 7ನೇ ದಿನ ಪುನರಾವರ್ತನೆಯಾಗುತ್ತದೆ. ಇದೇ ಮಾಡ್ಯುಲೋ ಗಣಿತ. 8 1 (ಮಾಡ್ಯುಲೋ 7) ಇದರ ಅರ್ಥ: (8-1) ನ್ನ 7 ರಿಂದ ಸರಿಯಾಗಿ ಭಾಗಿಸಬಹುದು. 15 1 (ಮಾಡ್ 7) ಇದರ ಅರ್ಥ: (15-1) ನ್ನ 7 ರಿಂದ ಸರಿಯಾಗಿ ಭಾಗಿಸಬಹುದು. 22 1 (ಮಾಡ್ 7) ಇದರ ಅರ್ಥ: (22-1) ನ್ನ 7 ರಿಂದ ಸರಿಯಾಗಿ ಭಾಗಿಸಬಹುದು. ಸಾಮಾನ್ಯವಾಗಿ xy (ಮಾಡ್ m ) ಆದರೆ, (x-y)£Àß m ನಿಂದ ಸರಿಯಾಗಿ ಭಾಗಿಸಬಹುದು. ಈ ಮೇಲಿನ ಹೇಳಿಕೆಯನ್ನು ಹೀಗೂ ಹೇಳಬಹುದು:x-y 0(ಮಾಡ್ m) ಇದನ್ನು “ಸರ್ವಸಮ” ಎಂದು ಓದುತ್ತೇವೆ. ಸರ್ವ ಸಮ ಆದಾಗ ( x-y)/ m = ಒಂದು ಪೂರ್ಣಾಂಕ ಈಗ ಯಾವುದೇ ಒಂದು ಧನ ಪೂರ್ಣಾಂಕವನ್ನು ಇನ್ನೊಂದು ಧನ ಪೂರ್ಣಾಂಕ (m) ನಿಂದ ಭಾಗಿಸಿದಾಗ ಉಳಿಯುವ ಶೇಷವು ಧನ ಪೂರ್ಣಾಂಕ ಆಗಿರುತ್ತದೆ. ಅದು {0,1,2,3,4…..(m-1)} ಗಣದಲ್ಲಿರುತ್ತದೆ. 0,1,2,….(m-1) ಈ ಸಂಖ್ಯೆಗಳನ್ನು ‘ಮಾಡ್ m’ ನ ಶೇಷಗಳೆನ್ನುವರು. Zm= {0,1,2,3,4…..(m-1)} ಇದನ್ನು ‘ಮಾಡ್ m’ ನ ಗಣ ಎನ್ನುವರು.

ವ್ಯಾಖ್ಯೆ: ಯಾವುದೇ ಸಂಖ್ಯೆಯನ್ನು ‘m’ ನಿಂದ ಭಾಗಿಸಿದಾಗ ಬರುವ ಶೇಷಗಳ ಗಣವನ್ನು “ಅವಶೇಷಗಳ ಗಣ” (‘residue set’) ಎನ್ನುವರು.

Z_m= {0,1,2,3,4…..(m-1)}

3.7.1 ಉದಾ 1: ಧನ ಪೂರ್ಣಾಂಕವೊಂದನ್ನು 10 ರಿಂದ ಭಾಗಿಸಿದಾಗ ಬರುವ ಶೇಷಗಳನ್ನು ಬರೆ.

ಪರಿಹಾರ:

10 ಭಾಜಕವಾದಾಗ ಬರುವ ಶೇಷಗಳು: 0,1,2,3….9

Z₁₀= {0,1,2,3,4,5,6,7,8,9}

ಮಾಡ್ಯುಲೋ ಕ್ರಮದಲ್ಲಿ ಸಂಕಲನ ಮತ್ತು ಗುಣಾಕಾರ:

ವ್ಯಾಖ್ಯೆ: m ಒಂದು ಮಾಡ್ಯುಲೋ ಆದರೆ..

ಸಂಕಲನದ ಸಂಕೇತ m

ಗುಣಾಕಾರದ ಸಂಕೇತ m

1. a +_m b r (= (a+b)/m ನ ಶೇಷ)

2. a _m b r (= (a*b)/m ನ ಶೇಷ)

3.7.1 ಉದಾ 2 : 10 +₁₂ 2 +₁₂ 3 ರ ಬೆಲೆ ಕಂಡುಹಿಡಿ..

ಪರಿಹಾರ:

10 +₁₂ 2 +₁₂ 3

=(10 +₁₂ 2) +₁₂ 3

=0+₁₂ 3( (10+2)/12 = ಶೇಷ ಸೊನ್ನೆ)

= 3(3/12 ರಲ್ಲಿ ಶೇಷ 3)

3.7.1 ಉದಾ 3 : 4 ₁₁ 3 ₁₁ 7 ಬೆಲೆ ಕಂಡುಹಿಡಿ..

ಪರಿಹಾರ:

4 ₁₁ 3 ₁₁ 7

=(4 ₁₁ 3) ₁₁ 7

= 1 ₁₁ 7((4*3)/11 ರಲ್ಲಿ ಶೇಷ = 1)

= 7 ( (1*7)/11 ರಲ್ಲಿ ಶೇಷ = 7)

3.7.1 ಉದಾ 4 : yy 1(ಮಾಡ್ 8) ಆದರೆ y ಯ ಬೆಲೆ ಕಂಡುಹಿಡಿ.

ಪರಿಹಾರ:

yy 1(ಮಾಡ್ 8)

(y*y ) ಯನ್ನು 8 ರಿಂದ ಭಾಗಿಸಿದಾಗ ಶೇಷ = 1 ಆಗಬೇಕು.

(y²-1) = 8

y=3.

ತಾಳೆ:

3₈ 3 =1( (3*3)/8 ರಲ್ಲಿ ಶೇಷ = 1)

3.7.2 ಕೇಲಿ ಕೋಷ್ಟಕ (Caley’s Table):

ಕೇಲಿ ಕೋಷ್ಟಕವು ಮಾಡ್ಯಲೋ ಗಣಿತ ಪದ್ಧತಿಯನ್ನು ಸೂಚಿಸುತ್ತದೆ.

ದತ್ತ ಗಣದಲ್ಲಿ ಮಾಡ್ಯಲೋ ಕ್ರಿಯಗಳಾದ ಸಂಕಲನ ಮತ್ತು ಗುಣಾಕಾರಗಳನ್ನು ಮಾಡಿದಾಗ, ಫಲಿತಾಂಶವನ್ನು ಒಂದು ತಃಖ್ತೆಯಲ್ಲಿ ನಿರೂಪಿಸಿದಾಗ, ಕೇಲಿ ಕೋಷ್ಟಕ ದೊರೆಯುವುದು.

ಕೇಲಿ ಕೋಷ್ಟಕ ದೊರೆಯುವ ಗಣ = Z₄ = {0,1,2,3}

ಸಂಕಲನ ಕ್ರಿಯೆಗೆ ಕೇಲಿ ಕೋಷ್ಟಕವನ್ನು ಬರೆಯುವಾ (ab) ಗೆ ಮಾಡ್ 4)

(ಮಾಡ್ 4) ರ ಶೇಷಗಳು 0,1,2 ಅಥವಾ 3 ಆಗಲು ಸಾಧ್ಯ a+₄ b ಯನ್ನು a =0,1,2,3 ಮತ್ತು b= 0,1,2,3. ಬೆಲೆಗಳಿಗೆ ಲೆಕ್ಕ ಹಾಕುವಾ

ಫಲಿತಾಂಶಗಳನ್ನು ಕೆಳಕಂಡಂತೆ ಒಂದು ತಃಖ್ತೆಯಲ್ಲಿ ಬರೆದಾಗ –

[ab ಮಾಡ್ 4] ಕ್ರಿಯೆಗೆ. (+₄)

0 +₄ 0 0 0 +₄ 1 1 0 +₄ 2 2 0 +₄ 3 3

1 +₄ 0 1 1 +₄ 1 2 1 +₄ 2 3 1 +₄ 3 0

2 +₄ 0 2 2 +₄ 1 3 2 +₄ 2 0 2 +₄ 3 1

3 +₄ 0 3 3 +₄ 1 0 3 +₄ 2 1 3 +₄ 3 2

bà	0	1	2	3
a	a +4 b =
0	0	1	2	3
1	1	2	3	0
2	2	3	0	1
3	3	0	1	2

ಗಮನಿಸಿ: ತಃಖ್ತೆಯಲ್ಲಿರುವ ಸಂಖ್ಯೆಗಳು Z₄= {0,1,2,3} ಗಣಕ್ಕೇ ಸೇರಿವೆ.

ಗುಣಾಕಾರ ಕ್ರಿಯೆಗೆ ಕೇಲಿ ಕೋಷ್ಟಕವನ್ನು ಬರೆಯುವಾ..(ab) ಮಾಡ್ 4). a X ₄ b ಯನ್ನು a =0,1,2,3 ಮತ್ತು b= 0,1,2,3. ಬೆಲೆಗಳಿಗೆ ಲೆಕ್ಕ ಹಾಕುವಾ. ಮೇಲೆ ನೋಡಿದಂತೆ, ಶೇಷಗಳ ಗಣ: Z₄= {0,1,2,3}.

ಫಲಿತಾಂಶಗಳನ್ನು ಕೆಳಕಂಡಂತೆ ಒಂದು ತಃಖ್ತೆಯಲ್ಲಿ ಬರೆದಾಗ –

[ab ಮಾಡ್ 4] ಕ್ರಿಯೆಗೆ ( X₄)

0 X₄ 0 0 0 X₄ 1 0 0 X₄ 2 0 0 X₄ 3 0

1 X₄ 0 0 1 X₄ 1 1 1 X₄ 2 2 1 X₄ 3 3

2 X₄ 0 0 2 X₄ 1 2 2 X₄ 2 0 2 X₄ 3 2

3 X₄ 0 0 3 X₄ 1 3 3 X₄ 2 2 3 X₄ 3 1

bà	0	1	2	3
a	a 4 b =
0	0	0	0	0
1	0	1	2	3
2	0	2	0	2
3	0	3	2	1

ಇಲ್ಲಿ ಕೂಡಾ ತಃಖ್ತೆಯಲ್ಲಿರುವ ಸಂಖ್ಯೆಗಳು Z₄= {0,1,2,3} ಗಣಕ್ಕೇ ಸೇರಿವೆ.

3.7.2 ಸಮಸ್ಯೆ1 : Q ={0,2,4,6,8} ಇದರ ಮೇಲಿನ ಮಾಡ್ 10 ರ ಕೇಲಿ ಕೋಷ್ಟಕವನ್ನು ರಚಿಸಿ.

ಪರಿಹಾರ:

ನಮಗೀಗ ab ಮಾಡ್ 10 ರ ಬೆಲೆಗಳು ಬೇಕು. a, b Q= {0,2,4,6,8}

(6+4)/10 ಆದಾಗ ಶೇಷ 0

(6+6)/10 ಆದಾಗ ಶೇಷ 2

(8+6)/10 ಆದಾಗ ಶೇಷ 4

ಈಗ

6 +₁₀ 4 0 6 +₁₀ 6 2 8 +₁₀ 6 4

ಇದೇ ರೀತಿ, a ,bUÀ¼À ಇತರ ಬೆಲೆಗಳಿಗೂ ಶೇಷವನ್ನು ಲೆಕ್ಕಹಾಕಬಹುದು.

bà	0	2	4	6	8
A	a +10 b=
0	0	2	4	6	8
2	2	4	6	8	0
4	4	6	8	0	2
6	6	8	0	2	4
8	8	0	2	4	6

3.7.2 ಸಮಸ್ಯೆ2 : A = {1,5,7,11} ಇದರ ಮೇಲಿನ ಮಾಡ್ 12 ರ ಕೇಲಿ ಕೋಷ್ಟಕವನ್ನು ರಚಿಸಿ.

ನಮಗೀಗ ab ಮಾಡ್ 12 ರ ಬೆಲೆಗಳು ಬೇಕು. a, b A ={1,5,7,11}

(7*7)/12 ಆದಾಗ ಶೇಷ 1

(7*11)/12 ಆದಾಗ ಶೇಷ 5

(11*11)/12 ಆದಾಗ ಶೇಷ 1

ಈಗ

7 ₁₂7 1 7 ₁₂ 11 5 11 ₁₂ 11 1

ಉಳಿದ a ಮತ್ತು b ಗಳ ಇತರ ಬೆಲೆಗಳಿಗೂ ಶೇಷವನ್ನು ಲೆಕ್ಕಹಾಕಿದಾಗ

bà	1	5	7	11
A	a 12 b =
1	1	5	7	11
5	5	1	11	7
7	7	11	1	5
11	11	7	5	1

3.7. ಕಲಿತ ಮುಖ್ಯಾಂಶಗಳು

ಕ್ರ.ಸಂ.	ಕಲಿತ ಮುಖ್ಯಾಂಶಗಳು
1	ಮಾಡ್ಯುಲೋ ಕ್ರಿಯೆಯ ವ್ಯಾಖ್ಯೆ.
2	ಮಾಡ್ಯುಲೋ ಸಂಕಲನ, ಗುಣಾಕಾರ
3	ಕೇಲಿ ಕೋಷ್ಟಕ.