6.12 ವೃತ್ತಗಳು – ಭಾಗ 3:

6.12.1: ವೃತ್ತದ ಕಂಸಗಳು

ಎರಡು ವೃತ್ತಗಳಲ್ಲಿ ಎರಡು ಕಂಸಗಳ ಕೇಂದ್ರೀಯಕೋನಗಳು ಒಂದೇ ಆಗಿದ್ದರೆ ಆ ಎರಡು ಕಂಸಗಳು ಸರ್ವಸಮ(congruent )

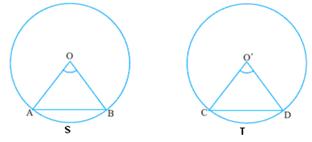
AOB = CO’D ಆದರೆ ಕಂಸ ASB = ಕಂಸ CTD

6.12.1 ಅಭ್ಯಾಸ 1: ಎರಡು ಕಂಸಗಳು ಸರ್ವಸಮವಾಗಿದ್ದರೆ ಅವುಗಳ ಜ್ಯಾಗಳು ಸಮ

ದತ್ತ: ಕಂಸ ASB = ಕಂಸ CTD

ಸಾಧನೀಯ: AB=CD

ಸಾಧನೆ:

1. OA = O’C, OB = O’D (ತ್ರಿಜ್ಯ) 2. AOB = CO’D (ಕಂಸಗಳು ಸರ್ವಸಮ) AOB CO’D (ಬಾ.ಕೋ.ಬಾ ಸ್ವಯಂಸಿದ್ಧ ) AB = CD

6.12.1 ಅಭ್ಯಾಸ 2: ಒಂದೇ ತ್ರಿಜ್ಯವಿರುವ ವೃತ್ತಗಳ ಎರಡು ಜ್ಯಾಗಳು ಸಮವಾಗಿದ್ದರೆ ಅವುಗಳ ಕಂಸಗಳು ಸರ್ವಸಮ.

ಗಮನಿಸಿ: ಇದು ಹಿಂದಿನ ಪ್ರಮೇಯದ ವಿಲೋಮ. (ಬಾ.ಬಾ.ಬಾ. ಸ್ವಯಂಸಿದ್ಧದಂತೆ AOB = CO’D ಎಂದು ತೋರಿಸಿ)

6.12.1: ವೃತ್ತಖಂಡದ ವಿಸ್ತೀರ್ಣ:

ಒಂದು ವೃತ್ತದ ತ್ರಿಜ್ಯ ‘r’ ಆದಾಗ : ವೃತ್ತದ ಪರಿಧಿ = 2r ಮತ್ತು ವೃತ್ತದ ವಿಸ್ತೀರ್ಣ = r^2. ಇಲ್ಲಿ ಎನ್ನುವುದು ಸ್ಥಿರಾಂಕವಾಗಿದ್ದು 22/7 (3.1428) ಎಂದು ಅಂದಾಜಾಗಿ ಲೆಕ್ಕಿಸುತ್ತೇವೆ. ಡಿಗ್ರಿಯು ಕಂಸ CSD ಯು ಕೇಂದ್ರದಲ್ಲಿ ಉಂಟುಮಾಡುವ ಕೇಂದ್ರೀಯ ಕೋನವಾಗಿರಲಿ (COD). 360^0 ಕೇಂದ್ರದ ಕೋನ ಆದಾಗ ವೃತ್ತದ ಪರಿಧಿ 2r ಆಗಿರುವುದರಿಂದ ^o ವು ಕೇಂದ್ರದ ಕೋನವಾದರೆ ಕಂಸದ ಉದ್ದ 1. CSD ಕಂಸದ ಉದ್ದ = () *r (ಏಕಮಾನ ಪದ್ಧತಿ) 360^0 ಕೇಂದ್ರದ ಕೋನ ಆದಾಗ ವೃತ್ತದ ವ್ಯಾಸ r^2 ವಿಸ್ತೀರ್ಣ ಆಗಿರುವುದರಿಂದ, ^o ವು ಕೇಂದ್ರದ ಕೋನವಾದರೆ ಅದು ಉಂಟುಮಾಡುವ ವೃತ್ತಖಂಡದ ವಿಸ್ತೀರ್ಣ: 2. 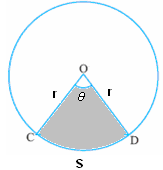CSDO ವೃತ್ತಖಂಡದ ವಿಸ್ತೀರ್ಣ (shaded ಚಿತ್ರದಲ್ಲಿನ ನೆರಳಿನ ಭಾಗ) = () *r^2= () * ()= [() *r]* = *ಕಂಸದ ಉದ್ದ*ತ್ರಿಜ್ಯ ಗಮನಿಸಿ: ರೇಡಿಯನ್ ಗಳು = 180^0 ಮತ್ತು x^0 = () ರೇಡಿಯನ್ ಗಳು

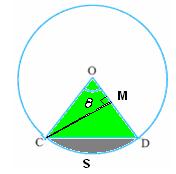
ಪಕ್ಕದ ಚಿತ್ರದಲ್ಲಿ COD = ಮತ್ತು CD ಯು ಅದು ಉಂಟುಮಾಡುವ ಜ್ಯಾ ಆಗ ತ್ರಿಕೋನದ ವಿಸ್ತೀರ್ಣ CDO = * ಪಾದ * ಎತ್ತರ = *DO*CM = *r*rsin= r^2*sin (CM = rsin : ಸೈನ್ ವಿವರಣೆಗೆ ಪಾಠ 7.1 ನೋಡಿ ) ಚಿತ್ರದಲ್ಲಿರುವಂತೆ: CSDO ವೃತ್ತಖಂಡದ ವಿಸ್ತೀರ್ಣ = CDO ತ್ರಿಕೋನದ ವಿಸ್ತೀರ್ಣ + CSD ವೃತ್ತಖಂಡದ ವಿಸ್ತೀರ್ಣ CSD ವೃತ್ತಖಂಡದ ವಿಸ್ತೀರ್ಣ= CSDO ವೃತ್ತಖಂಡದ ವಿಸ್ತೀರ್ಣ - CDO ತ್ರಿಕೋನದ ವಿಸ್ತೀರ್ಣ= () *r^2- () r^2*sin = r^2{(*) - ()} ಗಮನಿಸಿ : ಮೇಲಿನ ಲೆಕ್ಕಾಚಾರಕ್ಕೆ ಕೋನವು ಡಿಗ್ರಿಯಲ್ಲಿಯೇ ಇರಬೇಕು.

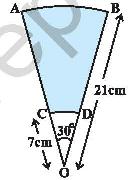
6.12 Problem 1: ತ್ರಿಜ್ಯ 21Cm ಮತ್ತು 7Cm ಇರುವ O ವೃತ್ತಕೇಂದ್ರವಿರುವ ಎರಡು ಏಕಕೇಂದ್ರೀಯ ವೃತ್ತಗಳ ಕಂಸಗಳು AB ಮತ್ತು CD. AOB= 30 ಆದರೆ ನೆರಳಿನ ಭಾಗದ ವಿಸ್ತೀರ್ಣ ಎಷ್ಟು?

ನೆರಳಿನ ಭಾಗ CABD ನ ವಿಸ್ತೀರ್ಣ = OCABDO ನ ವಿಸ್ತೀರ್ಣ - OCDO ನ ವಿಸ್ತೀರ್ಣ = () *21^2 - () *7^2 = [*]*[7*7*](3*3-1) ( 21^2=7^2 *3^2) ==

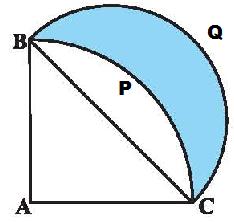
6.12 Problem 2: ಚಿತ್ರದಲ್ಲಿ ABC ಯು 14 cm ತ್ರಿಜ್ಯವುಳ್ಳ ವೃತ್ತ ಚತುರ್ಥಕವಾಗಿದೆ ಮತ್ತು ವ್ಯಾಸವಾಗಿರುವಂತೆ ಒಂದು ಅರ್ಧವೃತ್ತವನ್ನು ಎಳೆದಿದೆ. ಛಾಯೆಗೊಳಿಸಿದ ಭಾಗದ ವಿಸ್ತೀರ್ಣ ಎಷ್ಟು?

ನೆರಳಿನ ಭಾಗ BPCQB ನ ವಿಸ್ತೀರ್ಣ = ಅರ್ಧವೃತ್ತ BCQB ನ ವಿಸ್ತೀರ್ಣ- BCPB ನ ವಿಸ್ತೀರ್ಣ ಆದರೆ BCPB ವೃತ್ತಖಂಡದ ವಿಸ್ತೀರ್ಣ = ಕಾಲು ವೃತ್ತ ACPB ನ ವಿಸ್ತೀರ್ಣ - ABC ನ ವಿಸ್ತೀರ್ಣ BPCQB ನೆರಳಿನ ಭಾಗದ ವಿಸ್ತೀರ್ಣ = ಅರ್ಧವೃತ್ತ BCQB ನ ವಿಸ್ತೀರ್ಣ – (ಕಾಲು ವೃತ್ತ ACPB ನ ವಿಸ್ತೀರ್ಣ - ABC ನ ವಿಸ್ತೀರ್ಣ ) = ಅರ್ಧವೃತ್ತ BCQB ನ ವಿಸ್ತೀರ್ಣ – ಕಾಲು ವೃತ್ತ ACPB ನ ವಿಸ್ತೀರ್ಣ + ABC ನ ವಿಸ್ತೀರ್ಣ ಆದರೆ AC=AB=14 and BAC=90 ಪೈಥಾಗೊರಸ್ ಪ್ರಮೇಯದಂತೆ BC^2 = AB^2 + AC^2 BC(ವ್ಯಾಸ) = =. ಅರ್ಧವೃತ್ತ BCQB ನ ತ್ರಿಜ್ಯ = ಅರ್ಧವೃತ್ತ BCQB ನ ವಿಸ್ತೀರ್ಣ = *= **392= 154 ಕಾಲು ವೃತ್ತ ACPB ನ ವಿಸ್ತೀರ್ಣ = 14^2( 14cm ತ್ರಿಜ್ಯವಿರುವ ವೃತ್ತದ ಕಾಲು ಭಾಗದ ವಿಸ್ತೀರ್ಣ)= **14*14=154 ABC ನ ವಿಸ್ತೀರ್ಣ = *14*14 = 98 ( ತ್ರಿಕೋನದ ಪಾದ ಮತ್ತು ಎತ್ತರ ಒಂದೇ ) ನೆರಳಿನ ಭಾಗ BPCQB ನ ವಿಸ್ತೀರ್ಣ = 154 -154 + 98 =98

6.12 ಕಲಿತ ಅಂಶಗಳು

ಸಂಖ್ಯೆ	ಕಲಿತ ಅಂಶಗಳು
1	ಕಂಸಗಳ ಸರ್ವಸಮತೆ
2	ಕಂಸದ ಉದ್ದ,ವೃತ್ತಖಂಡದ ವಿಸ್ತೀರ್ಣಗಳ ಸೂತ್ರ