6

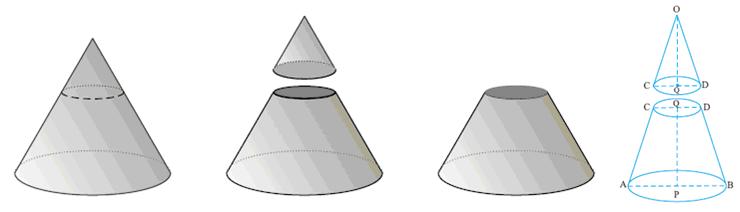
6.15 Solid figures:

In our daily life, we come across several challenging questions such as

1. What is the capacity of a water/petrol tanker, or a tanker carrying milk?

2. How to measure the heap of grains/sand stacked on the floor, against wall, at the corner of wall?

3. What is the requirement of paint to paint a pillar?

4. How much cloth is required to cover a tent?

5. What is the volume/mass of earth?

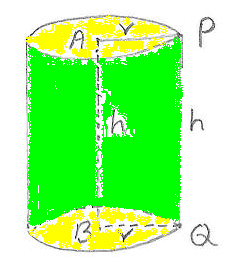
6.15.1 Cylinder

Surface Area of Cylinder

In your daily life you must have come across objects like water pipes, iron rods and Road roller. They are all cylindrical in shape. They may be hollow like pipes, or solids like rods and road rollers. They all have circular planes at two ends.

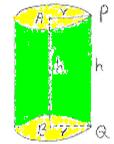
In the figure given below, AB is the axis of cylinder. PQ is the height of the cylinder. AP and BQ (AP=BQ) are the radius of the two circular planes.

Features of the right circular cylinders are:

1. They have two circular planes (base and top)

(Yellow color-AP and BQ)

2. These circular planes are parallel to each other

and have same radius(r)

3. The line joining the centers of circular planes

(AB) is the axis of the cylinder

4. The curved surface joining the circular planes is the lateral surface

(Green color)

5. All the points on the lateral surface are equidistant from the axis

6. The distance between the circular planes is the height of the cylinder

Imagine we cut the outer surface of this cylinder across and

if we spread across, we get a rectangle similar to ABCD.

Breadth of the rectangle is equal to the length of the cylinder (AB=h).

Length of the rectangle = circumference of the circular plane=P =2r

Lateral surface are of cylinder = area of rectangle =

Length*Breadth = P*h = 2 r *h =2rh

Total surface area of cylinder =

Area of circular plane of one side (top)

+ Lateral surface area + Area of circular plane of another side (bottom)

= r²+2rh+r²= 2r²+2rh=2r(r+h) sq units

For easy calculation we use approximate value for =22/7 in all our problems.

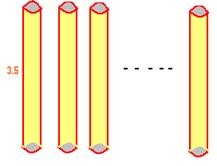
6.15.1 Problem 1: A mansion has 12 cylindrical pillars 0f 3.5 meters height and of circumference of 50cms. Find the cost of painting the lateral surface of the pillars at Rs 25 per Sq.meter.

Solution:

Let us use all the values in single unit of meters

Lateral surface of one pillar = Ph = .5*3.5 = 7/4 Sq. meter

Since there are 12 pillars, total area to be painted = 12*7/4 = 21 sq. meters

Painting cost = (area*rate) =21*25 = Rs 525

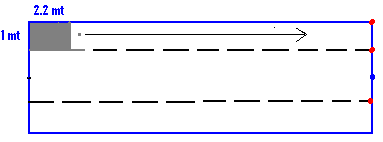
6.15.1 Problem 2: A roller having 70cms as diameter and length of 1 meter is used to level the playground in your school. If it makes 200 complete revolutions what is the area of playground?

Solution:

The radius of roller = 35cms or .35 meters ( d=2r =70)

Lateral surface area of roller = 2rh

= 2*(22/7)*.35*1 = 44*.05 = 2.2 sq. meters

Since roller makes 200 rounds,

total area of playground = 200*2.2 = 440 sq. meters

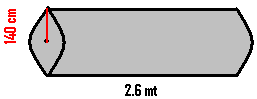
6.15.1 Problem 3: A Petrol tanker is made of sheet metal. If the tank’s length is 2.6 meters and the radius of the cylindrical tank is 140cm. How many sq meters of sheet metal is required to make the tank?

Solution:

Since tanker is closed on all sides,

we are required to calculate total surface area = 2r(r+h)=

2*(22/7)*1.4*(1.4+2.6) = 2*22*.2*4 = 35.2 Sq. meters

Volume of cylinder

We have seen that volume of cube = length*breadth*height =(area of the base)*height

Similarly volume of a cylinder = (area of base)*height =(area of the circular plane)*height

= (r²)*h = r²h cubic units

Note that volume is always represented in cubic units

6.15.1 Problem 4: You must have observed that on the petrol tanker they mention the capacity of the tanker. If the capacity of tanker mentioned on a petrol tanker = x liters and length of the tanker is =y meters. Find out the diameter of the tanker in meters

Solution: Do it yourself by taking measurements of a tanker(x, y)

6.15.1 Problem 5: A Paint manufacturer sells paints in 1 litre cylindrical tins of diameter 14cm. How many such tins can he store one above

the other in a store room of height 3.245 meters

Solution:

First we need to find the height of the tins

Since diameter of the tin 14cm its radius(r)= 7cm

Volume of tin = r²h = (22/7)7*7*h = 154h

It is given that tin’s capacity is 1 liter

We know 1 liter = 1000cc

154h =1000

i,e h =6.49cm

Since the store room is of height 3.245 meters we can stack 50 (=3.245*100/6.49) tins one above the other

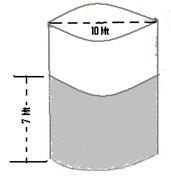
6.15.1 Problem 6: The height of water level in a circular well is 7 meters and its diameter is 10 meters. Calculate the volume of water stored in the well.

Solution:

Since the diameter of the well is 10 meters. Its radius = 5 meters

Volume of well = r²h = (22/7)*5²*7 = 22*25 = 550 cubic meters = 5, 50,000 liters

( 1cu meter = 100*100*100 cc and 1000cc = 1 liter )

6.15.2 Circular cones

Surface Area of Cone

The heap of grains, heap of sand, ice cream introduce us the concept of cones in our daily life.

Like in the case of cylinders we need to know the methods of calculating surface area and the volume of cones

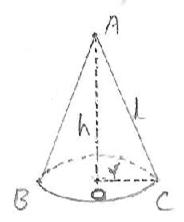
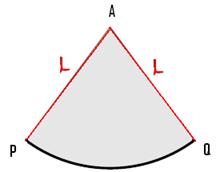
In the adjacent figure we have a right circular cone

Its properties are

1. A cone has only one circular plane and is of radius OC =r

2. It has one vertex (A) which is the intersection point of

cone’s axis (OA) and the slant height (CA=l)

3. The line joining the centre of circular plane to the vertex is the height (OA=h)

4. The curved surface which connects the vertex and the circular edge of the circular base is the lateral surface area

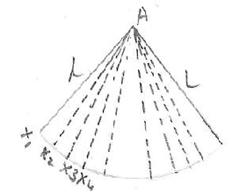
If we cut a cone along the edge and spread across, we get a sector of a circle as shown below.

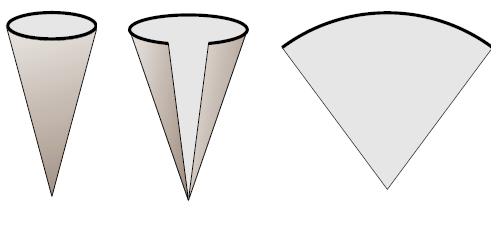
The section (APQ in the figure on the left) is formed by an arc of radius equal to slant height l of the cone.

The sector APQ can be imagined to be made up of very small triangles (AX₁X₂, AX₂X₃,,AX₃X₄, …..)

as shown in the figure on the right hand side.

Though the sectors X₁X₂, X₂X₃, X₃X₄ are not straight lines,

they tend to become straight lines when the circular section APQ is divided into small portions.

They form the base of small triangles.

Note area of AX₁X₂= (1/2)*base*height =(1/2)*base*l

Lateral surface area of the cone = Sum of areas of several small triangles

= (1/2)*B₁l +(1/2)*B₂l+(1/2)*B₃l+ …….+(1/2)*B₁l

= (1/2)l [B₁+ B₂+ B₃+ ………+ B_n]

But [B₁+ B₂+ B₃+ ………+ B_n] = perimeter of the base of the cone = 2r

Lateral (curved) surface area of the cone =(1/2) l *2r= rl

Total surface area of cone = area of circular plane of base + lateral surface area = r² +rl = r² +rl=r(r+l)

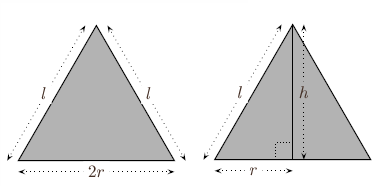
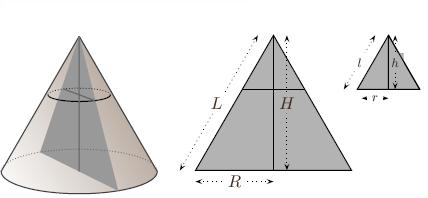
The relationship between base, height and slant height in a cone:

As in the figure on the right hand side

Let base radius of the cone =r

Let height of the cone =h

Let slant height of the cone =l

From Pythagoras theorem

l²= h²+r²

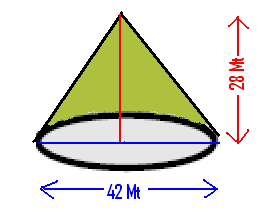
6.15.2 Problem 1: A conical tent was is put up for a show supported by a pole of height 28 meters at the center. The diameter of the base is 42 meters. Find the cost of the canvas used at the rate of Rs.20/- per sq mts

Solution:

Here r=21( d=2r =42): h=28

We need to find the curved surface area.

For that we need to know the slant height of the tent

The slant height is the hypotenuse of the triangle formed by the radius as the base and height

By Pythagoras theorem

(hypotenuse)²= (base)²+(height)²= (21)²+(28)²= 441+784 =1225 =(35)²

slant height = l = 35 meters

Lateral (curved) surface area of the cone =rl =(22/7)*21*35 = 22*3*35 =2310 Sq. meters

Cost of the canvas = area*rate = 2310*20 = Rs 46,200

6.15.2 Problem 2: A factory was asked to use sheet metal to make a conical object of slant height 8 meters with diameter of the base as 12 meters. How much sheet metal is required?

Solution:

Here r=6( d=2r =12), l=8

Total surface area of cone =r(r+l)

= (22/7)*6*(6+8) = (22/7)*6*14 = 22*6*2 =264 Sq. meters

Volume of Cone

By observations and actual measurements

we notice that if a cylinder and a cone have same circular base and same height then,

volume of a cylinder is equal to three times the volume of the cone.

(observe the adjoining figure)

Volume of cone

= (1/3)*volume of cylinder

= (1/3)* (r²)h cubic units ( we have seen volume of cylinder =r²h)

= (1/3)* (area of base) *h

6.15.2 Problem 3: A worker in a factory was given a meter long cylindrical rod of radius 3.5cm. He was asked to melt the material and make from that, cones of radius 1cm and height 2.1 cm. How many cones can he produce?

Solution:

The measurements of cylindrical rod are (r=3.5, h=100cm)

Volume of cylinder = r²h = (22/7)*3.5*3.5*100 = 22*3.5*.5*100=3850cc

After melting this, he is asked to produce cones of sizes(r=1, h=2.1)

The volume of the cone to be manufactured = (1/3)* r²h

= (1/3)*(22/7)*1*1*2.1 = 22*.1 =2.2cc

Number of cones the worker can produce

= (Volume of the melted rod)/Volume of Cone to be made

= 3850/2.2

= 1750 pieces

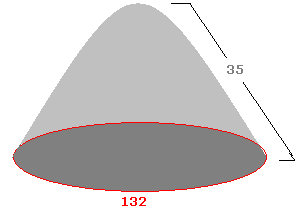
6.15.2 Problem 4: A heap is farmed when a farmer pours food grains on a ground. The slanted height of heap is 35 feet. The circumference of the base is 132ft. He sells the food grains based on the volume. Name the solid formed and find the volume.

Solution:

The heap formed is of cone shape.

We are required to find the volume of the cone. We are given circumference of the base and its slant height.

In order to calculate the volume We need to find the radius and the height.

Since circumference = 2r,r = (circumference)/ 2 = 132*7/(2*22) = 3*7=21

The slant height is the hypotenuse of the triangle formed by the radius as the base and height.

By Pythagoras theorem,

(hypotenuse)²= (base)²+(height)²

(height)²=(hypotenuse)²-(base)²= (35)²-(21)²= 1225-441=784 =(28)²

height = h = 28 feet

Volume of the heap(cone) = (1/3)* (r²)h = (1/3)*(22/7)*21*21*28=22*21*28 =12,936 cubic feet

Finding the area and volume of an object similar to the shape of a bucket (Frustum):

Looking at the above figures we notice

1. Curved surface area of APBDQC(Frustum) = Curved surface area of the cone APBDOCA – Curved surface area of the cone CQDOC

2. Volume of APBDQC(Frustum) = Volume of the cone APBDOCA – Volume of the cone CQDOC

Relationship between measures of original cone and the cone cut off:

Observe the figure on the right hand side

Let base radius, height and the slant height of large cone be

R,H,L and that of small cut off cone be r,h,l respectively.

Since two triangles in the figure are similar,

the sides opposite to equal angles are proportional

Hence r/R = h/H=l/L

Thus,

If from the top of a cone, a smaller cone is cut off by slicing parallel

to the base, then the base radius, height and the slant height of

two cones are proportional.

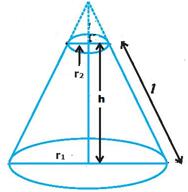
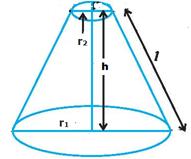
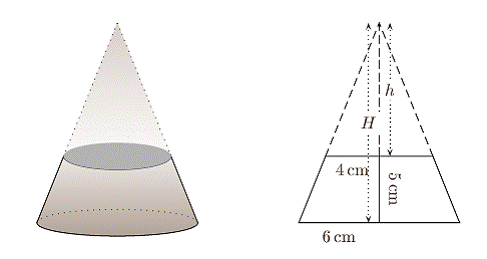
6.15.2 Frustum:

In the first figure radius of circular base is r_1.If we cutthe cone somewhere in the middle we get a frustum as shown in second figure. The height of frustum is h, slant height is l, radius of circular base is r₁and radius of circle at the top is r₂ Then:

Volume of frustum = h(r₁²+ r₂²+ r₁r₂)

Curved surface area of frustum = l(r₁ + r₂)

Total surface area of frustum

= Curved surface area of frustum +Area of circular base +Area of circular portion at the top

= [l(r₁ + r₂)+ (r₁²+ r₂²)] = [l(r₁ + r₂)+ (r₁²+ r₂²)]

Figure 1 Figure 2

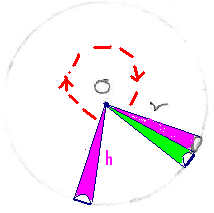
6.15.2 Problem 5: A heap of grains is stored against a wall, in the inner corner of a wall and outer corner of wall having circumference of 30, 15 and 45 ‘Hasta’(Unit of measurement) respectively. If the height of heap is 6 Hasta, tell the size of the heap (Lilavati Shloka 237)

Solution:

The heap is of the cone shape.

The base of the heap is part of a circle and hence we need to find the radius.

Note that their base is part of the same circle having base of half of circle, quarter of circle and 3/4^th of a circle

2r = 60 , For simplicity let us assume =3, then r = 60/6 = 10

Volume of cone = (1/3)* (area of base) *h ( It is given that height = 6)

Volume of heap with circumference of 30

= {1/2}*(1/3)*(r²)*h= (1/6)*3*10²*6 = 300

Volume of heap with circumference of 15

= {1/4}*(1/3)*(r²)*h= (1/12)*3*10²*6 = 150

Volume of heap with circumference of 45

= {3/4}*(1/3)*(r²)*h= (3/12)*3*10²*6 = 450

6.15.2 Problem 6: The Radius of the top circle of a frustum is 4 cm and the radius of its bottom is 6cm. The height of frustum is 5cm. compute its volume.

Solution:

Let the height of larger cone and smaller cone be H and h respectively.

Since the radii and heights are proportional

h/H = 4/6 =2/3

From the given data and from the figure we note H-h =5

(H-5)/H = 4/6 =2/3

1-(5/H) = 2/3

-(5/H) = (2/3)-1 = -(1/3)

H = 15

h = 10

Volume of larger cone = (1/3)* (R²)H = (1/3)(6²)15

Volume of smaller cone = (1/3)* (r²)H = (1/3)(4²)10

Volume of frustum =

Volume of larger cone - Volume of smaller cone

= (1/3) (36*15-16*10)

= (1/3) (380) cubic cms

6.15.3 Sphere

The objects such as Football, cricket ball. and marbles introduce us the concept of sphere

The properties of sphere are

1. Sphere has a centre.

2. All the points on the surface of the sphere are at equidistance from centre of the sphere.

3. The equidistance is the radius of the sphere.

4. A plane passing through the centre of the sphere divides the sphere in to two equal parts called hemispheres.

Surface area of sphere:

By observation and actual measurement

we conclude that surface area of the sphere is four times the area of circular plane surface passing thorough the diameter

(the plane which cuts sphere in two equal parts)

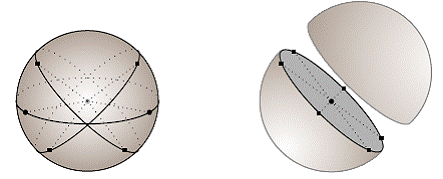
Surface area of sphere = 4 r² square units

(area of circular plane = area of circle = r²)

It is interesting to note that the surface area of a sphere is equal to curved surface area

of a cylinder just containing it(Refer Adjacent figure)

6.15.3 Problem 1: A building has hemispherical dome whose circumference is 44mtrrs. Calculate the cost of painting at Rs. 200 per square meters

Solution:

We know Circumference = 2r

r = circulferenc/2 = (1/2)*44*(7/22) = 7 meters

Surface area of sphere = 4r² = 4*(22/7)*7*7 = 4*22*1*7 = 616 Sq meters

Surface area of dome (hemisphere) = half of surface area of sphere = 308 sq meters

Cost of painting = area*rate = 308*200 = 61,600 Rs.

Volume of sphere:

Who has not heard of water melon which is rich in Vitamin A, C , Iron and Calcium.

Have you observed how a vendor cuts a water melon before you decide to buy one?

He makes an incision and cuts through the water melon to take a piece out(cone shape) similar to what is shown in the adjacent figure.

We shall introduce similar concept while working with sphere.

The sphere can be concluded to be consisting of small cones of height equal to the radius of the sphere with circular base as can be inferred from the adjoining figure.

We have learnt that volume of small cone

= 1/3 (area of circular base of cone)*height

(volume of cone = 1/3*Bh where B is area of base of cone and h is the height of the cone)

Volume of 1^st cone = 1/3 B₁r

Volume of 2^nd cone= 1/3 B₂r

…

Volume of nth cone =1/3 B_nr

Volume of sphere = Sum of volume of small cones

= (1/3) B₁r+(1/3) B₂r.......... (1/3) B_nr

= (1/3)*r(B₁+B₂.......... +B_n)

= (1/3)*r*(Surface area of sphere) ( If we join all the small cones together side by side, the bases of small cones become the surface area of sphere)

= (1/3)*r*4r² = 4/3 r³(Surface area of sphere= 4r²)

Note that if a cone is inscribed within the sphere as in the adjacent figure, then the volume of

the sphere is four times the volume of the cone.

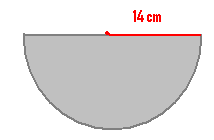
6.15.3 Problem 2: A hemisphere bowl of radius of 14 cm is used as a measure to prepare sweets in a shop. . How many liters of ghee can it hold?

Solution:

Here r = 21 cm. Note hemisphere is half of sphere

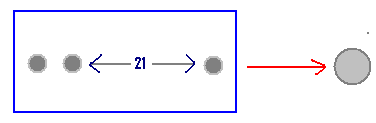
Volume of bowl which is a hemisphere = 2/3 r³= 2/3 *22/7*14*14*14 = 5749.3 cc = 5.75 liters ( 1000 cc = 1 liter)

6.15.3 Problem 3: 21 lead marbles having 2cm radius are melted to make a big sphere. Find the volume of the sphere and its radius

Solution:

Volume of 1 marble = 4/3 r³= (4/3)*(22/7)*2*2*2 = 32*22/21

Volume of 21 marble = 21*32*22/21 = 32*22 = 704cc

Since marbles were melted and a sphere is made,

Volume of sphere = 4/3 r³=(4/3)*(22/7)r³ = 88/21r³

r³ = 704*(21/88) ( the volume of sphere is given to be 704cc)

=168 r =5.52cm (approximate value got using a calculator)

Verification:

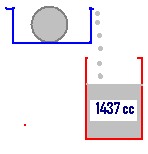
Volume of sphere of radius 5.52cm = 4/3 r³= (4/3)*(22/7)*5.52*5.52*5.52 = 704(Calculator was used to get the approximate value)

6.15.3 Problem 4 : When a iron shot-put ball was immersed in a jar it spilled out approximately 1437cc of water. Find out the diameter of the shot-put.

Note, the water spilled out is equal to volume of shot-put.

Solution:

Volume of shot-put = 1437cc

4/3 r³=1437cc

i,e (4/3)*(22/7)r³ =1437

r³ = 1437*21/(4*22) =343

r=7 cm

Therefore diameter of the shot-put is 14 cm

Verification:

Volume of shot-put of radius 7cm = 4/3 r³ = (4/3)*(22/7)*7*7*7 = (4/3)*22*7*7 =1437

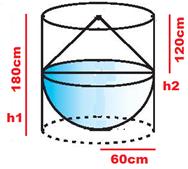
6.15.3 Problem 5: An object has been created with a cone of height 120 cm on top of a semi sphere of radius 60 cm. Find out the volume of water in cubic meters remaining in the cylinder, when this object is immersed in a cylinder having radius of 60cm and height of 120cm.

Solution:

Radius of cylinder= Radius of semi sphere= Radius of cone = 60 cm=r

Height of Cylinder = h1= 180 cm ; Height of cone =h2=120 cm

Water remaining in cylinder = volume of cylinder- volume of semi sphere- volume of cone

= r²h1 - r³-r²h2

= r²(h1- r -h2) = r²( 180- *60 -*120)

= *60*60*(180-40-40)

= *60*60*100= *10000 113*10000 Cubic cm = 1.13 cubic meter.

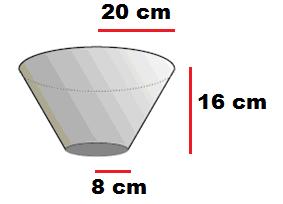
6.15.3 Problem 6: A utensil is made from a sheet of metal in the shape of a bucket with top open. The height of bucket is 16cm. The radii of bottom and top portions are 8cm and 20 cm respectively. The bucket needs to be filled with milk. Find out the buying cost of milk in the bucket if the rate of milk is Rs.20 per liter. Also find out the cost of metal sheet, if the rate of metal sheet is Rs 8 per 100 sq.cm.( Take = 3.14).

Solution:

Write a rough sketch as shown in the figure. Here h h=16, r₁= 8 and r₂=20

l== = 20

Volume of utensil =h(r₁²+ r₂²+ r₁r₂)

=*3.14*16(20²+ 8²+ 20*8)= *3.14*16*(624)

= 3.14*16*208 10449 cc=10.449 liter

Cost of milk 10.449*20 209 Rs.

Total Surface area of utensil = Curved surface area of utensil + Area of circular bottom

= l(r₁ + r₂)+ r₁²= [ l(r₁ + r₂) + r₁² ] =3.14[ 20*28+64] = 3.14*624= 1959.36 sq.cm.

Cost of metal sheet = 1959.36*8* Rs. 156

6.15 Summary of learning

If l, b, h are sides of cuboid and a is the side of cube h and l are the height and slant height of geometrical figure then

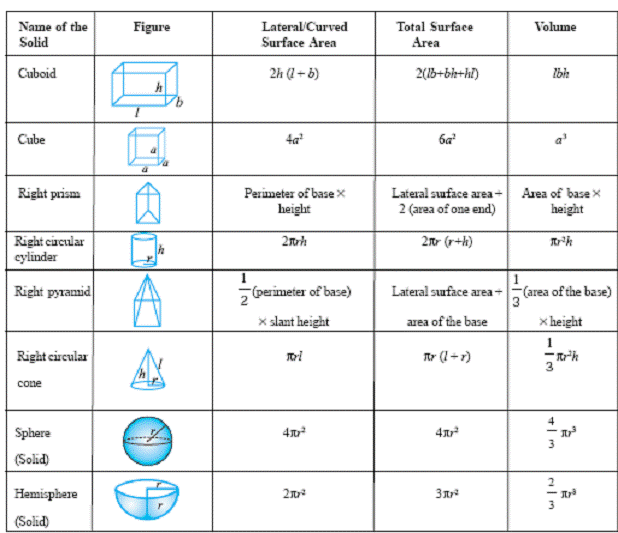
Additional points:

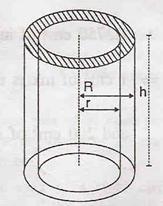
6.15.1 Hollow Cylinder

Have you observed water pipes made of cement or cylindrical water tanks built on houses ? They all have one thing in common that is they are all hollow and have one internal and another external curved surface.

Let R be the external radius, r be the internal radius (Note R>r) and h be the height of the cylinder

No.	Explanation	Expression
1	Thickness of the hollow cylinder	R-r
2	Area of cross section = (Area of outer circular plane – Area of inner circular plane)	R² - r² = (R² - r²)
3	External curved surface area	2Rh
4	Internal curved surface area	2rh
5	Total surface Area = External+ internal+ top plane+ bottom plane	2Rh + 2rh + 2(R² - r²)
6	Volume of solid portion = ( External volume – inner volume)	R²h - r²h = (R² - r²)h

6.15.1 Problem 7: A hose pipe of cross sectional area of 2 sq.cm. delivers 1500 litres in 5 minutes. What is the speed of water in meters/second through the pipe?

Solution:

Cross section can be thought of as the area of a circular plane = r² = 2sq.cm.

Water discharged in 5 minutes = 1500 liters = 1500*1000 cc (1 liter = 1000cc)

This can be thought of as the volume of water collected for 5 minutes in a pipe of length h whose cross section is 2sq.cm.

r²h = 1,500,000 = 2h (r² = 2)

h = 750,000cm = 7500 meters (1m = 100cm)

Since this is the water collected in 5minutes (=300Sec), water collected in 1 second = 7500/300 = 25meters

6.15.1 Problem 8: A rectangular water tank measuring 80cmx60cmx60cm is filled from a pipe of cross sectional area of 1.5sq cm,

the water emerging at 3.2mts/sec. How long does it take to fill the tank?

Hint:

1. Calculate the volume of tank(l*b*h)

2. Calculate the volume of water flowing through a pipe of circular plane area of 1.5sq cm in one minute at 3.2mts/sec.

3. Divide the volume of the tank (arrived at step 1) by the volume of water (arrived at step 2)

6.15.1 Problem 9: A metal pipe has a bore (inner diameter) of 5cm. The pipe is 5mm thick throughout. Find the weight (in kg) of 2 meters of the pipe if 1 cubic cm of metal weighs 7.7gm.

Solution:

r = 2.5cm, R = 2.5+0.5 cm = 3cm, h = 200cm

Volume of solid portion =(R² - r²)h = 22/7*(9-6.25)*200 = 1728.57 cu cm

Weight in kg = (volume in cc * weight in gram /cc)/1000 = 1728.57*7.7/1000 = 13.31 kg

We divided the result by 1000 to get the answer in KG