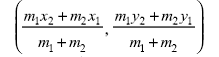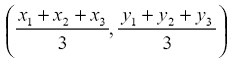7.2 Distance between two points and Section
Formula:
7.2.2
Dividing the line in the given ratio: Is it possible to divide a line of
length 10cm in 3:4 ratio using only scale? To do this one
needs to divide this line into 7 equal parts and then identify points at 3 parts and 4 parts respectively. For that we
need to have exact value of ![]() *3. But its value is 4.28571… Hence we cannot
identify a exact point
corresponding to this value while using only the scale. However we can do this based on
geometry.
*3. But its value is 4.28571… Hence we cannot
identify a exact point
corresponding to this value while using only the scale. However we can do this based on
geometry.
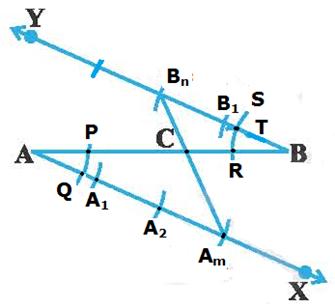
Steps to divide a
line segment in the ratio of m:n in general:
|
No. |
Steps |
Figure |
|
1 |
Let
AB be a line segment (say 11cm). We need to divide it in the ratio of m:n(say
3:2) |
|
|
2 |
Draw a line AX making an acute angle with AB( Ex 300
or 45o) |
|
|
3 |
Steps to draw parallel line to AX: i)
With the help
of divider, draw an arc PQ of suitable
radius cutting the lines AX and AB ii)
Using the same
radius drawn an arc RS cutting line AB
at R iii)
With the length
PQ as radius, cut arc RS at T iv)
Join B and T
and extend it up to Y Now BY is parallel to AX. |
|
|
4 |
Identify
points on AX to make ‘m’ equal parts
such that AA1=A1A2=A2A3=A3A4=…Am-1Am
(say m=3) |
|
|
5 |
With length as AA1 identify points on BY to make ‘n’ equal parts
such that BB1=B1B2=B2B3=B3B4=…Bn-1Bn(=AA1)(
say n=2) |
|
|
6 |
Join
Am and Bn ( say A3 and B2).
Let this line cut AB at C then AC:CB=m:n(In the example 3:2). |
|
|
7 |
Proof: In
But
|
|
|
|
Note:
In the example AB=11Cm; m=3, n=2 (Also Am= A3 and Bn=
B2) |
|
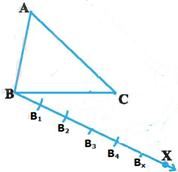
Steps to construct a triangle whose
corresponding sizes are ![]() th of given triangle:
th of given triangle:
|
No. |
Steps |
Figure |
|
1 |
Let ABC be the given triangle. We need to
construct another similar triangle whose corresponding sides are |
|
|
2 |
Below
BC draw an another line BX by making an acute angle with BC( Say 300 or 45o) |
|
|
3 |
Divide
BX such that BB1=B1B2=B2B3=B3B4=…Bx-1Bx(Here
x= maximum of ‘m’ and ‘n) Now we have two
situations |
|
|
|
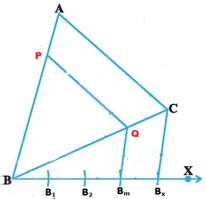
Situation 1: i)
Join Bx (=Bn) and C ii)
From Bm draw parallel line to BxC . Let it cut BC at Q iii)
From Q draw parallel line to AC. Let it cut BA at P Sides
of Note
that |
|
|
|
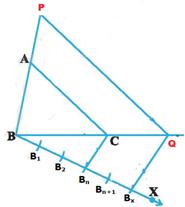
Situation 2: i)
Join Bn and C ii)
From Bx(=Bm) draw
parallel line to BnC . Let it cut extended BC
at Q iii)
From Q draw parallel line to AC. Let it cut extended BA at P Sides
of Note
that |
|
Note that when ![]() <1 the constructed triangle is smaller than the given
triangle and when
<1 the constructed triangle is smaller than the given
triangle and when ![]() >1 the constructed triangle is bigger than the given
triangle.
>1 the constructed triangle is bigger than the given
triangle.
7.2.1
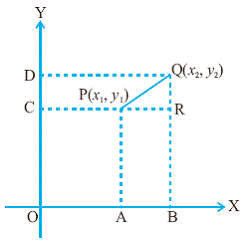
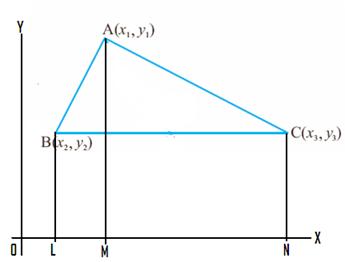
Distance between two points: We have learnt how to plot points on a plane
in a graph sheet. There are many instances where we need to find the distance
between two points (length of the line segment joining two points).
|
We
know that any point can be represented in terms of co-ordinates of x and y. Let
P (x1,y1) and Q (x2,y2)
be the two points. We
are required to find the length of the line PQ. Draw
PA and QB perpendicular to x axis from P and Q respectively. Note
that OA = x1 and Draw
PC and QD horizontal to Y axis from P and Q respectively. Note
that OC = y1 and OD = y2 Produce
CP to meet BQ at R. PR
= OB-OA = x2-x1 QR
= OD-OC = y2-y1 Since
PQ2 =
PR2+RQ2= (x2-x1)2+ (y2-y1)2
This formula is called 'distance
formula' |
|
Corollary: What if one point is the origin (0,0) ?
The distance of a
point P (x,y) from the
origin O(0,0) is OP = ![]() (x2+ y2)
(x2+ y2)
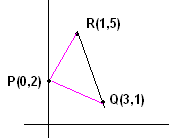
7.2 Problem 1: Find the value of k if P(0,2) is equidistant from Q(3,k) and R(k,5)
Solution:
|
PQ = PR = Since
PQ=PR it follows that 9
+k2-4k+4 = k2+9 On
simplification we get k = 1 The point P(0,2) is equidistant from Q(3,1) and R(1,5). |
|
7.2 Problem 2: State the special property of the
triangle formed by three points A(10,-18), B(3,6) and
C(-5,2)
Solution:
|
AB = AC = BC = Since AB=AC it is
clear that the triangle formed by the given three points is an isosceles
triangle |
|
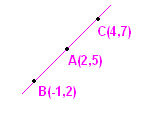
7.2 Problem 3: Using distance formula show
that points A(2,5), B(-1,2) and C(4,7) are collinear
|
Hint: Show that
BA+AC = BC (Verify by plotting points that they are collinear) |
|
7.2 Problem 4: Find the co-ordinates of the Circumcenter of a
triangle ABC whose vertices are A(4,6),B(0,4) and
C(6,2)
|
Hint: Let
O(x,y) be the Circumcenter. Then OA= Solution: OA2
= (x-4)2+(y-6)2=x2-8x+16+y2-12y+36 OB2
= (x-0)2+(y-4)2=x2+y2-8y+16 OC2
= (x-6)2+(y-2)2=x2-12x+36+y2-4y+4 Equating
OA2 = OB2 We get 2x+y =9 Equating
OA2 = OC2 We get x-2y = -3 By
solving the above two equations we get x=3 and y=3. Hence
O(3,3) is the Circumcenter
of |
|
Section
Formula:
This section is
about finding a point on a line such that the point divides the line in the
given ratio.
|
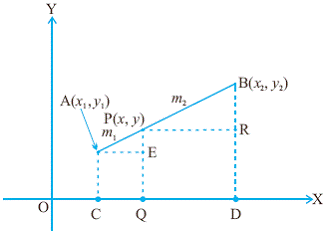
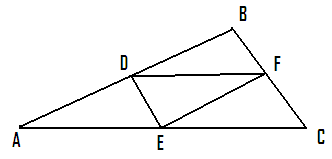
Let
AB be the line joining the point A (x1, y1) and B(x2,
y2). We
are required to find a point P(x, y) on the line AB such that it divides AB
in the given ratio of m1:m2. From
A, P and B draw perpendiculars to the x-axis and let these perpendiculars
meet x- axis at C,Q and D respectively. From
A and P draw parallel lines to x axis to meet PQ at E and BD at R. If
P is a point on AB dividing it in the given ratio of m1:m2,
then AP/PB = m1/m2 It
is clear from the adjacent figure that, AE/PR = PE/BR=AP/PB = m1/m2 --------à(1) AE
= OQ-OC = x-x1 : PR =
OD-OQ = x2-x PE =
QP-QE(=CA) = y-y1 BR =
DB-DR = y2-y Thus
by substituting values in (1) we get AE/PR = (x-x1)/(x2-x) = PE/PR = (y-y1)/
(y2-y) = m1/m2 --------à(2) By
taking first and last expression in (2), we have (x-x1)/(x2-x)
= m1/m2
Similarly,
by taking second and last expression in (2) we get y = (m1y2+ m2y1)/(m2+m1) Thus
the co-ordinates of point P, which divides the line joining points A(x1,
y1) and B(x2, y2) in the ratio of m1:m2
are given by: {(m1x2+ m2x1)/(m1+m2), (m1y2+ m2y1)/(m1+m2) } This
is known as ‘section formula’. |
|
1. What are the
co-ordinates of midpoint of AB (i.e. when m1:m2 = 1:1)?
It is {(x2+x1)/2),
(y2+ y1)/2}: (Mid point formula)
Note: The above formula can be used to
show that the quadrilateral formed by joining the midpoints of adjacent sides
of a quadrilateral is a parallelogram.
2. What are the
co-ordinates of the point which divides the line in the ratio of k:1?
It is {(kx2+x1)/(k+1), (ky2+ y1)/(k+1)}
7.2 Problem 5: Find the ratio in which the point P(11,15) divides the line segment joining the points A(15,5)
and B(9,20)
Solution:
|
Let
P divide the line AB in the ratio of k:1 x1=15,
y1=5, x2=9, y2=20,x=11, y=15 We
have seen above that the co-ordinates of the point which divides a line in the
ratio of k:1 is {(kx2+x1)/(k+1),
(ky2+ y1)/(k+1)}
Hence
the point divides the given line in the ratio of 2:1 |
|
7.2 Problem 6: Find the co-ordinates of points which trisects
the line joining A(6,-2) and B(-8,10)
Hint:
|
We
are required to find the co-ordinates of P and Q such that AP=PQ=QB (1:1:1) This
problem needs to be solved in two steps: 1. Find the co-ordinates of P(x1,y1) such that AP:PB = 1:2. 2. Find the co-ordinates of Q(x2,y2)
such that AQ:QB = 2:1 They
are P (4/3,2) and Q (-10/3,6) |
|
7.2 Problem 7: In triangle ABC, D(-2,5)
is mid point of AB, E(2,4) is mid point of BC and F(-1,2) is mid point of AC.
Find the
co-ordinates of A,B and C.
|
Hint: Let
A =(x1,y1), B=(x2,y2) and C=(x3,y3) Since
D is mid point of AB, (x1+x2)/2 = -2 and (y1+y2)/2
= 5 Since
E is mid point of BC, (x2+x3)/2 = 2 and (y2+y3)/2
= 4 Since
F is mid point of AC, (x1+x3)/2 = -1 and (y1+y3)/2
= 2 By
solving these three equations we get x1=
-5, x2=1, x3= 3 y1=
3, y2=7, y3= 1 Thus
the vertices are A(-5,3), B(1,7) and C(3,1) |
|
7.2.3
Area of a triangle given the co-ordinates of a triangle
|
As
in the adjoining figure let A (x1, y1), B(x2,
y2) and C(x3, y3) be the three vertices of a
triangle. We are required to find the area of triangle ABC. Let
BL, AM and CN be perpendiculars from the vertices B, A and C to x-axis.
From
the figure Area of Triangle ABC = =Area
of trapezium BLMA + Area of trapezium AMNC - Area of trapezium BLNC =
1/2(BL+AM)LM + 1/2(AM+NC)MN - 1/2(BL+NC)LN =
1/2(y2+ y1) (x1- x2) + 1/2(y1+
y3) (x3- x1) - 1/2(y2+ y3)
(x3- x2) =
1/2[x1(y2-
y3) + x2(y3- y1) +x3(y1-
y2)]
--------- (By
rearranging the terms) Note
that if A B and C are collinear then area is zero. |
|
7.2 Problem 8: If D(3,-1), E(2,6), F(-5,7) are the mid points of the sides of ![]() ABC, find the area of
ABC, find the area of ![]() ABC.
ABC.
|
Let us calculate the
area of Area of =1/2[-3+16+35] =1/2(48) = 24 sq units Since the area of
Area of |
|
7.2 Problem 9: If the consecutive verticies
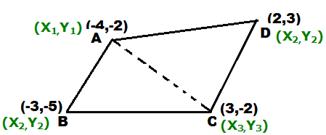
of triangle are (-4,-2), (-3,-5),(3,-2) and (2,3) then what is its area?
|
Draw a rough diagram of quadrilateral ABCD. Join A and C, then we get
two triangles Area of triangle =
Area of quadrilateral = 2 Area of 2 triangles = |
|
7.2
Summary of learning
|
No |
Points to
remember |
|
1 |
The
distance between points P (x1,y1)
and Q (x2,y2) is
= |
|
2 |
The co-ordinates of the point which divides A(x1,y1)
and B (x2,y2) in the given ratio of m1:m2
are
|
Co-ordinates
of centroid:
|
We
have learnt that the centroid divides the median in the ratio of 2:1 (Refer
to Section 6.4) Given
the three vertices of a triangle let us calculate the co-ordinates of the
centroid. In
the adjoining figure A (x1, y1), B(x2, y2)
and C(x3, y3) AD
is one median and G is the centroid which divides AD in the ratio 2:1. We
are required to find the co-ordinates of G. Since
AD is median BD = DC
Since
G(x,y) divides AD in 2:1 (m1=2 and m2=1)
We have x
= {2(x2+x3)/2)+1. x1}/(2+1) = (x2+x3+x1)/3 y
= {2(y2+y3)/2)+1. y1}/(2+1) = (y2+y3+y1)/3 Thus
the co-ordinates of centroid are
|
|
7.2 Problem 8: Find the third vertex of a triangle
if two of its vertices are at A(-3,1) and B(0,-2) and the centroid is at the origin.
Solution:
Let C(x3,
y3) be the third vertex
We know that the co-ordinates
of centroid are
x = (x1+x2+x3)/3
and
y = (y1+y2+y3)/3.
Since the
co-ordinates of origin are (0,0)
It follows that
x1+x2+x3
= 0 and y1+y2+y3
= 0
By substituting the
values for co–ordinates we have
x1+x2+x3=
-3+0+ x3=0
![]() x3 = 3
x3 = 3
y1+y2+y3=
1-2+ y3=0
![]() y3 = 1
y3 = 1
Thus (3,1) is the third vertex.