7.3 ರೇಖೆಯ ಸಮೀಕರಣ (Equation of a line):

ಪೀಠಿಕೆ:

ಪಾಠ 7.1 ರಲ್ಲಿ ಸರಳರೇಖೆಯ ಸಮೀಕರಣ y=mx+c ಸಾಮಾನ್ಯ ರೂಪದಲ್ಲಿರುತ್ತದೆ ಎಂದು ಕಲಿತಿದ್ದೇವೆ. ಹಾಗೆಯೇ ಸರಳರೇಖೆಯ ಮೇಲಿನ ಪ್ರತಿಯೊಂದು ಬಿಂದುವೂ ರೇಖಾಸಮೀಕರಣವನ್ನು ತೃಪ್ತಿಪಡಿಸುತ್ತದೆ ಮತ್ತು ಯಾವುದೇ ಬಿಂದುವು ಸಮೀಕರಣವನ್ನು ತೃಪ್ತಿಪಡಿಸಿದರೆ ಆ ಬಿಂದುವು ಆ ಸರಳರೇಖೆಯ ಮೇಲಿರುತ್ತದೆ.

ಯಾವುದೇ ಸರಳ ರೇಖೆಯು x ಅಕ್ಷದ ಜೊತೆಗೆ ಉಂಟುಮಾಡುವ ಕೋನವನ್ನು ‘ರೇಖೆಯ ಓರೆ’ ( ‘inclination’ ) ಎಂದು ಕರೆಯುತ್ತೇವೆ.

ಚಿತ್ರ 1	ಚಿತ್ರ 2	ಚಿತ್ರ 3
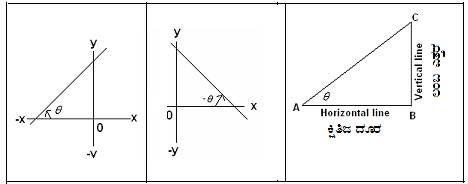
ರೇಖೆಯ ಓರೆ ಯನ್ನು ಅಪ್ರದಕ್ಷಿಣ ದಿಕ್ಕಿನಲ್ಲಿ ಅಳತೆ ಮಾಡಿದರೆ ಅದು ಧನವಾಗಿರುತ್ತದೆ (ಚಿತ್ರ 1), +ve	ರೇಖೆಯ ಓರೆ ಯನ್ನು ಪ್ರದಕ್ಷಿಣ ದಿಕ್ಕಿನಲ್ಲಿ ಅಳತೆ ಮಾಡಿದರೆ ಅದು ಋಣವಾಗಿರುತ್ತದೆ (ಚಿತ್ರ 2), -ve	‘ರೇಖೆಯ ಇಳಿಜಾರು’(slope) ವು ಲಂಬ ಎತ್ತರ ಮತ್ತು ಕ್ಷಿತಿಜ ದೂರ ಇವುಗಳ ನಡುವಿನ ಅನುಪಾತವಾಗಿರುತ್ತದೆ (ಚಿತ್ರ 3)
ಯಾವುದೇ ಇಳಿಜಾರು, ಕ್ಷಿತಿಜ ರೇಖೆಗೆ ಉಂಟುಮಾಡುವ ಕೋನ ಆಗಿದ್ದರೆ ಆಗ ರೇಖೆಯ ಇಳಿಜಾರು = ಲಂಬ ಎತ್ತರ / ಕ್ಷಿತಿಜ ದೂರ = BC/AB=tan (8.1 ಪಾಠ ನೋಡಿ) ಈ ಅನುಪಾತವನ್ನು m ಅಕ್ಷರದಿಂದ ಗುರುತಿಸುತ್ತೇವೆ.

ಗಮನಿಸಿ:

1. X ಅಕ್ಷ ದ ’ರೇಖೆಯ ಇಳಿಜಾರು” = 0 (tan=0 as =0⁰)

2. Y ಅಕ್ಷ ದ ’ರೇಖೆಯ ಇಳಿಜಾರು’ = ಅನಿರ್ದಿಷ್ಟ(tan= =90⁰)

3. ಯಾವುದೇ ರೇಖೆಯು, ಅಪ್ರದಕ್ಷಿಣ ದಿಕ್ಕಿನಲ್ಲಿ X ಅಕ್ಷ ದೊಡನೆ ಲಘುಕೋನ ಉಂಟುಮಾಡಿದರೆ ಆಗ ಆ ’ರೇಖೆಯ ಇಳಿಜಾರು’ ಧನವಾಗಿರುತ್ತದೆ (ಚಿತ್ರ 1)

4. ಯಾವುದೇ ರೇಖೆಯು, ಪ್ರದಕ್ಷಿಣ ದಿಕ್ಕಿನಲ್ಲಿ X ಅಕ್ಷ ದೊಡನೆ ಲಘುಕೋನ ಉಂಟುಮಾಡಿದರೆ ಅಥವಾ ಅಪ್ರದಕ್ಷಿಣ ದಿಕ್ಕಿನಲ್ಲಿ X ಅಕ್ಷ ದೊಡನೆ ವಿಶಾಲಕೋನ ಉಂಟುಮಾಡಿದರೆ ಆಗ ಆ ’ರೇಖೆಯ ಇಳಿಜಾರ” ಋಣವಾಗಿರುತ್ತದೆ

(- tan= tan(-)) (ಚಿತ್ರ 2)

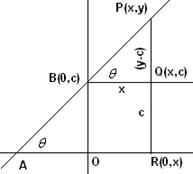
ನಿರ್ದಿಷ್ಟ ಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವ ಸರಳ ರೇಖೆಯ ಇಳಿಜಾರು’(Slope of a straight line passing through fixed points)

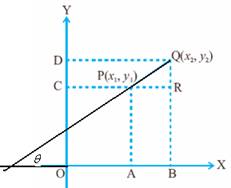
P (x1,y1) ಮತ್ತು Q (x2,y2) ಎರಡು ದತ್ತ ಬಿಂದುಗಳಾಗಿರಲಿ. PQ ರೇಖೆಯ ’ರೇಖೆಯ ಇಳಿಜಾರು’ ಕಂಡುಹಿಡಿಯಬೇಕಾಗಿದೆ. QP ಯನ್ನು x-ಅಕ್ಷವನ್ನು ಸಂಧಿಸುವಂತೆ ಅದನ್ನು ವೃದ್ಧಿಸಿದಾಗ ಅದು x-ಅಕ್ಷ ದೊಡನೆ ಕೋನವನ್ನು ಉಂಟುಮಾಡಲಿ CR || x-ಅಕ್ಷವಾಗಿರುವುದರಿಂದ = QPR m = tan = QR/PR= ಲಂಬ ಎತ್ತರ/ಕ್ಷಿತಿಜ ಎತ್ತರ = (y2- y1)/ (x2- x1) = (y1- y2)/ (x1- x2) =ಅಭಿಮುಖ ಬಾಹು/ಪಾರ್ಶ್ವ ಬಾಹು
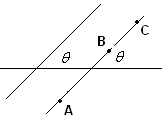
ಗಮನಿಸಿ: 1. ಸಮಾನಾಂತರ ರೇಖೆಗಳ ’ರೇಖೆಯ ಇಳಿಜಾರು” ಒಂದೇ ಆಗಿರುತ್ತದೆ. (ಸಮಾನಾಂತರ ರೇಖೆಗಳು x-ಅಕ್ಷದೊಡನೆ ಒಂದೇ ’ರೇಖೆಯ ಓರೆ’ ಯನ್ನು ಹೊಂದಿರುತ್ತದೆ) ವಿಲೋಮವಾಗಿ ಹೇಳುವುದಾದರೆ ಎರಡು ರೇಖೆಗಳ ’ರೇಖೆಯ ಇಳಿಜಾರು” ಒಂದೇ ಆಗಿದ್ದರೆ ಅವು ಸಮಾನಾಂತರ ರೇಖೆಗಳಾಗಿರುತ್ತವೆ. 2. ಮೇಲಿನ ಹೇಳಿಕೆಗಳಿಂದ ಸರಳರೇಖೆಯ ಮೇಲಿನ ಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವ ರೇಖೆಯ ’ರೇಖೆಯ ಇಳಿಜಾರು ಒಂದೇ ಆಗಿರುತ್ತದೆ.
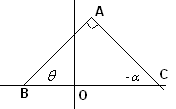
ಎರಡು ಲಂಬ ರೇಖೆಗಳ ’ರೇಖೆಯ ಇಳಿಜಾರು’ ಗಳ ಸಂಬಂಧ: BAAC ಆಗಿರಲಿ. ವು AB ಯು x ಅಕ್ಷದೊಡನೆ ಉಂಟುಮಾಡುವ ’ ರೇಖೆಯ ಓರೆ’ ಆಗಿರಲಿ. - ವು AC ಯು x ಅಕ್ಷದೊಡನೆ ಉಂಟುಮಾಡುವ ’ ರೇಖೆಯ ಓರೆ’ ಆಗಿರಲಿ. (ಪ್ರದಕ್ಷಿಣವಾಗಿ ಉಂಟುಮಾಡುವ ಲಘುಕೋನ) AB ’ರೇಖೆಯ ಇಳಿಜಾರು’ = tan = AC/AB CA ’ರೇಖೆಯ ಇಳಿಜಾರು’ = - tan = - (AB/AC) AB ’ರೇಖೆಯ ಇಳಿಜಾರು’ * CA ’ರೇಖೆಯ ಇಳಿಜಾರು’ = (AC/AB)*-(AB/AC) = -1. 3. ಆದುದರಿಂದ ಎರಡು ಲಂಬರೇಖೆಗಳ ’ರೇಖೆಯ ಇಳಿಜಾರು’ ಗಳ ಗುಣಲಬ್ಧ -1; ವಿಲೋಮವಾಗಿ ಹೇಳುವುದಾದರೆ ಎರಡು ರೇಖೆಗಳ ’ರೇಖೆಯ ಇಳಿಜಾರು’ ಗಳ ಗುಣಲಬ್ಧ -1 ಆಗಿದ್ದರೆ ಅವು ಪರಸ್ಪರ ಲಂಬರೇಖೆಗಳಾಗಿರುತ್ತವೆ

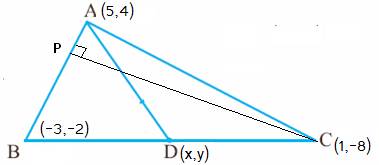
7.3 ಸಮಸ್ಯೆ 1: A(5,4),B(-3,-2) ಮತ್ತು C(1,-8) ಗಳು ತ್ರಿಕೋನ ABC ಯ ಶಿರೋಬಿಂದುಗಳು.

(I) AB ಗೆ ಲಂಬವಾಗಿರುವ ’ರೇಖೆಯ ಇಳಿಜಾರು’ ಎಷ್ಟು?.

(II) ಮಧ್ಯ ರೇಖೆ AD ’ರೇಖೆಯ ಇಳಿಜಾರು’ ಎಷ್ಟು?.

(III) AC ಗೆ ಸಮಾನಾಂತರವಾಗಿರುವ ’ರೇಖೆಯ ಇಳಿಜಾರು’ ಎಷ್ಟು?.

ಪರಿಹಾರ:

(I) AB ’ರೇಖೆಯ ಇಳಿಜಾರು’ = (4-(-2))/(5-(-3)) = (6/8) = 3/4 ಎರಡು ಲಂಬರೇಖೆಗಳ ’ರೇಖೆಯ ಇಳಿಜಾರು’ ಗಳ ಮೊತ್ತ -1 ಮತ್ತು ABCP ಆಗಿರುವುದರಿಂದ CP ’ರೇಖೆಯ ಇಳಿಜಾರು’ = -4/3 (II) AD ಯ ’ರೇಖೆಯ ಇಳಿಜಾರು’ ಕಂಡುಹಿಡಿಯುವ ಮೊದಲು BC ಯ ಮಧ್ಯಬಿಂದು D(x,y) ಯನ್ನು ಕಂಡುಹಿಡಿಯಬೇಕು. D ಯು BC ಯ ಮಧ್ಯಬಿಂದು ಆಗಿರುವುದರಿಂದ x= (-3+1)/2 = -1 ; y = (-2+(-8))/2 = -5 D(-1,-5). AD ’ರೇಖೆಯ ಇಳಿಜಾರು’ = ( 4-(-5))/(5-(-1)) = 9/6 = 3/2 (III) AC ’ರೇಖೆಯ ಇಳಿಜಾರು’ = (4-(-8))/(5-1) = 12/4 = 3 AC ಗೆ ಸಮಾನಾಂತರವಾಗಿರುವ ಯಾವುದೇ ಸರಳ ರೇಖೆಯ ’ರೇಖೆಯ ಇಳಿಜಾರು’ = 3

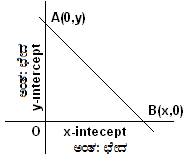
ಅಂತ: ಛೇದಗಳು:

ಪಾಠ 7.1 ರಲ್ಲಿ ಅಂತ: ಛೇದ ದ ಕುರಿತು ಕಲಿತಿರುವೆವು: ಯಾವುದೇ ಸರಳರೇಖೆಯು x ಅಕ್ಷವನ್ನು ಕಡಿಯುವುದೋ ಆ ಬಿಂದುವಿನಿಂದ O(0,0) ಗೆ ಇರುವ ದೂರವೇ x- ಅಂತ: ಛೇದ (x ನಿರ್ದೇಶಾಂಕ). ಯಾವುದೇ ಸರಳರೇಖೆಯು x ಅಕ್ಷವನ್ನು ಕಡಿಯುವುದೋ ಆ ಬಿಂದುವಿನಿಂದ O(0,0) ಗೆ ಇರುವ ದೂರ(ಎತ್ತರ)ವೇ y- ಅಂತ: ಛೇದ (y ನಿರ್ದೇಶಾಂಕ).

ಸರಳ ರೇಖೆಯ ಸಮೀಕರಣ:

ಯಾವುದೇ ಸರಳ ರೇಖೆಯ ಸಮೀಕರಣವು y=mx+c ಸಾಮಾನ್ಯ ರೂಪದಲ್ಲಿರುತ್ತದೆ ಎಂದು ಮತ್ತು ’ರೇಖೆಯ ಇಳಿಜಾರು’ ಎಂದರೆ ಎನು ಎಂದೂ ನಾವು ಕಲಿತಿರುವೆವು.

1. ರೇಖೆಯ ಇಳಿಜಾರು- ಅಂತ: ಛೇದ ರೂಪದಲ್ಲಿ

P ಎನ್ನುವುದು ನಿರ್ದೇಶಾಂಕ (x,y) ಹೊಂದಿರುವ ಬಿಂದುವಾಗಿರಲಿ. AB ಎನ್ನುವ ಸರಳರೇಖೆಯಾಗಿದ್ದು ಮತ್ತು ಅದರ ’ ರೇಖೆಯ ಓರೆ’ ಆಗಿರಲಿ. ಅದರ y- ಅಂತ: ಛೇದ c ಆಗಿರಲಿ, OB=c=RQ PQ = PR-QR = y-c ಚಿತ್ರದಲ್ಲಿರುವಂತೆ PBQ = m = tan = PQ/BQ = (y-c)/x mx = y-c ಅಂದರೆ y = mx+c ಎನ್ನುವುದು AB ರೇಖೆಯ ಸಮೀಕರಣ.

7.3 ಸಮಸ್ಯೆ 2: ರೇಖೆ 2x-5y+4=0 ನ ರೇಖೆಯ ಇಳಿಜಾರು ಮತ್ತು y ಅಂತ: ಛೇದ ಕಂಡುಹಿಡಿ

ಪರಿಹಾರ:

ದತ್ತ ರೇಖೆ 2x-5y+4=0 ( y = ()x+() { y=mx+c)}

ರೇಖೆಯ ಇಳಿಜಾರು

ರೇಖೆಯ y ಅಂತ: ಛೇದ

7.3 ಕಲಿತ ಸಾರಾಂಶ

ಕ್ರ.ಸಂ.	ಕಲಿತ ಮುಖ್ಯಾಂಶಗಳು
1	P (x1,y1) ಮತ್ತು Q (x2,y2) ಆಗಿರುವಾಗ m = (y1- y2)/(x1- x2)
2	ರೇಖೆಯ ಇಳಿಜಾರು m ಮತ್ತು y- ಅಂತ: ಛೇದ c ಆದರೆ, ಆಗ ಆ ರೇಖೆಯ ಸಮೀಕರಣ y = mx+c