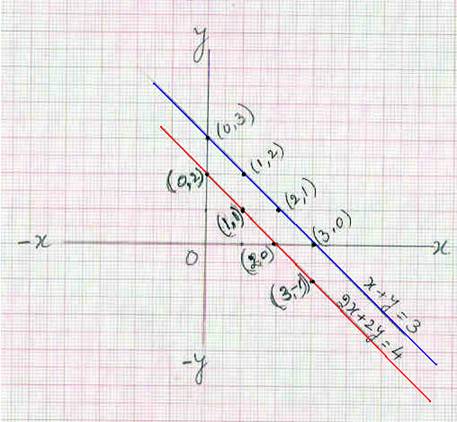7.4 Graphical method of solving
Simultaneous linear equations:
Introduction :
We have seen in earlier sections(2.7) that a linear equation is represented a by a
line on the graph sheet and hence the name linear equation.
We have also learnt that we need
two equations to solve simultaneous liner equations. From these observations, it becomes logical that
why not represent the linear equations
graphically and then find a point
on the graph sheet which cuts the lines representing the given linear equations.
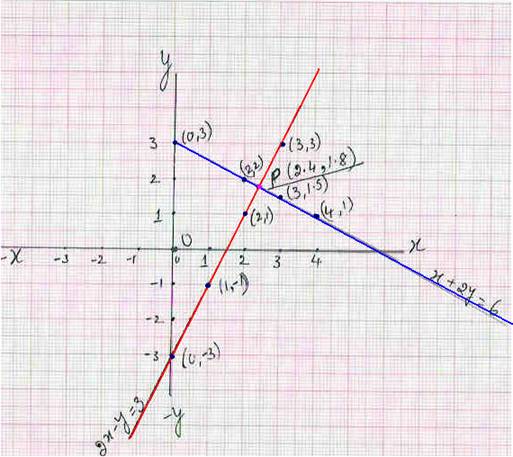
7.4 Problem 1: Solve 2x-y =3 and x+2y =6
graphically.
Solution:
|
Consider the equation 2x-y =3
and draw a graph for this line on a graph sheet. Step 1 : Convert the given equation in
the form of y = (i.e. LHS will
have only y) Given
equation 2x-y =3 i.e. -y =3-2x(transposition). Multiply both sides by -1 to get y=2x-3 Step 2 : For few values of x
(though 2 is enough) get values of y
and record them in a table as shown below:
Step 3 : Plot the points represented by (x, y)
coordinates on a graph sheet. Step
4 : Join the points to get a straight line to represent the line y=2x-3(or
2x-y=3) Note
: 1.
Though only two points are enough to draw a straight line, we have calculated
more values of (x, y) to indicate that there are many solutions to 2x-y =3. 2.
It is also clear from the graph that many coordinates like (0.5,-2) on the line 2x-y =3 satisfy the given equation. We
need another line crossing this line on the graph so that we get an
intersection point .The coordinates of this point will give unique solution
to these 2 equations. Let us draw graph for x+2y = 6(Steps
5 to 7 given below) Step
5 :
Transpose x to get
2y = 6-x i.e. y = (6-x)/2 Step 6 : For few values of x,
calculate corresponding values of y and record them in a table as shown
below(repetition of Step 2):
|
|
||||||||||||||||||||||||||||||
|
Step
7 : Plot the points represented by (x, y)
coordinates on a graph sheet and join
them to get a straight line. Step 8 : Let this and the
earlier line meet at point P( If the 2 lines don’t meet then extend
the 2 lines in both directions so that they meet) Step 9 :
Find the coordinates of P which is (2.4,1.8). |
|||||||||||||||||||||||||||||||
Conclusion:
The solution the given equation is x =2.4 and y =1.8
Verfication:
Solve the above 2 equations using
elimination method:
2x-y = 3 ====è(1)
x+2y = 6 ====è(2)
Multiply (1) by 2: 4x-2y =6 ====è(3)
-----------
Add (2) & (3) 5x+0 = 12
-----------
i.e. x= 2.4
By Substituting 2.4 for x in (2).
We get 2.4+2y=6 and on
transposition we get 2y =3.6(=6-2.4) i.e. y=1.8
This is exactly the coordinates of
point P, which was obtained after drawing the graph
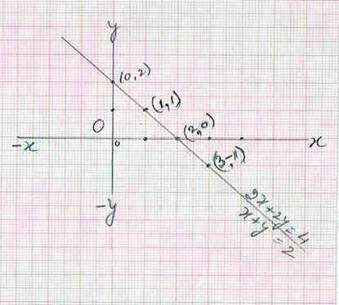
7.4 Problem 2 : Solve 2x+2y = 4 and x+y
= 2 graphically
Solution:
|
Given equation 2x+2y =4 Step 1: (Express the equation as
y=) :2y = 4-2x (On transposition) i.e.
y = 2-x (On simplification) Step 2: For few values of x get
values of y and record them in a table as shown below:
Step 3: Draw a graph using these
(x, y) coordinates to represent the line 2x+2y=4 Step 4: Take 2nd equation x+y =2 i.e. y =2-x ( On
transposition) Step 5: Since this equation is
same as2x+2y=4, The (x,y) coordinate pairs can be
obtained from step 2.
Step 6 :
Since the coordinates are same as in Step 2, this line is same as the one that was drawn in step
3(The two lines are collinear) Conclusion : There are
infinite values of (x, y) which
satisfy the given set of equations. Hence there is no unique
solution to the simultaneous liner equations: 2x+2y = 4 and x+y = 2. |
|
Verification: Refer 2.14 problem 3.
7.4 Problem 3: Solve 2x+2y = 4 and x+y = 3
graphically
Solution:
|
Given equation is 2x+2y =4 Step 1: (Express the given
equation as y=)i.e. 2y =4-2x (On transposition) i.e. y = 2-x
(On simplification)) Step 2: For few values of x
calculate values of y and record them in a table as below:
Step
3: Draw a graph using these (x, y) coordinates to represent the line 2x+2y=4 Step 4: Consider the 2nd
equation x+y =3 i.e. y =3-x (On transposition) Step 5: For few values of x,
calculate values of y and record them in a table as below: (repetition of Step 2)
Step
6: Draw a graph using these (x, y) coordinates to represent the line x+y=3 (repetition
of step 3) Step 7 : Since these two lines
are parallel, they never meet Conclusion : There are no values
of x and y which satisfy both the given equations: 2x+2y = 4 and x+y =3 |
|
Verification: Refer 2.14 problem 4.
Observations: The graphs of
a1 x+ b1 y = c1
and
a2 x+b2 y =
c2
Will be
1. Parallel if they have no
solution
2. Coincident (concurrent) if they
have infinite solutions
3. Intersecting if they have a
unique solution
7.4 Problem 4 : The
cost of manufacturing x articles is Rs 50+3x. The selling price of x
articles is 4x. on a graph
sheet draw two graphs, first for the cost of manufacturing and second for selling
price. From the
graph find out the number of articles to be manufactured and sold to break
even(no profit and no loss)
Solution:
The equation for cost of
manufacturing articles is CP=3x+50.
The equation for selling price of
articles is SP=4x
Using the below mentioned scale,
draw two straight lines on a graph sheet representing the above two equations (CP
and SP)
x axis for number of
articles : 1 cm = 10 articles
y axis for Rupees 1cm =
10Rs
Table for CP
|
x
à |
0 |
10 |
20 |
|
CP
à |
50 |
80 |
110 |
|
(x,
y) |
(0,5) |
(1,8) |
(2,11) |
Table for SP
|
x
à |
0 |
10 |
20 |
|
SP
à |
0 |
40 |
80 |
|
(x,
y) |
(0,0) |
(1,4) |
(2,18) |
We note that these two straight
lines meet at (5,20)
This means that the cP of manufacturing 50
articles = SP of 50 articles. Thus the break even happens at the manufacture of
50 articiles
Verification: if x = 50 then CP = 3x+50=150+50=200
With x=50, SP = 4x=200
Thus for x=50, CP=SP=Rs 200 and
hence our solution is correct.
7.4 Summary of learning
|
No |
Points studied |
|
1 |
Simultaneous
linear equations can also be solved by drawing graph for each of the lines. |
|
2 |
The
intersection of the two lines gives the solution. |
|
3 |
If
the lines are parallel then there is no solution |
|
4 |
If
the lines are concurrent then there are infinite solutions |