1.2. Squares and square roots:

 

We have studied in previous classes that the area of a rectangle

is = length * breadth

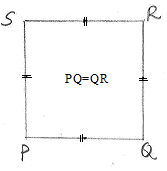
When the length and breadth are equal we have a Square figure like the adjacent figure (PQ=QR)

Its area is PQ*QR= length*length = (length)2

 

 

 

Have you observed some thing unique about the numbers 1, 4, 9, 16 among 1,2,3,4,5…

Let us look at the multiplication table:

 

Multiplication table for 2

Multiplication table for 3

Multiplication table for 4

Multiplication table for 5

2*1 = 2 

3*1 = 3 

4*1 = 4

5*1 = 5

2*2 = 4  

3*2 =6 

4*2 =8

5*2 =10

2*3 = 6

3*3 = 9 

4*3 =12

5*3 =15

 

3*4 = 12 

4*4 =16

5*4 =20

 

 

4*5 = 20

5*5 =25

 

What do you observe? The numbers 4,9,16 and 25 are squares of 2, 3, 4 and 5 respectively.

Definition : A perfect square is a number which can be expressed as  a product of two same  numbers

Also notice:

12 = 1 = (-1)2

22 = 4 = (-2)2

32 = 9 = (-3)2

Square numbers are integers raised to the power of 2. They are of the form n2

 

Properties of Square numbers:

 

1.      The digit in the units place of a perfect square is always 0,1,4,5,6,9( 1,4,9,16,25,36,49,64,81,100,121…)

2.      Numbers ending with 2, 3, 7 or 8 cannot be perfect squares (43, 62, 57, 98 are not perfect squares)

3.      The square of an even number is always even (4, 16, 36, 64, 100 …)

4.      The square of an odd number is always odd (1, 9, 25, 49, 81, 121…)

5.      The square numbers do not have (2, 3, 7, and 8) as digits in their unit place.

6.      A perfect square cannot have a reminder of 2 when divided by 3(400÷3 gives a reminder of 1. 324÷3 gives a reminder of 0. Since 455÷3 gives a reminder of 2, it cannot be a perfect square).

7.      Number of zeros at the end of a perfect square is always even (Ex. 100, 2500, etc).

8.      If n is a perfect square and p is a prime number then p*n cannot be a perfect square (81 is a prefect square but 2*81, 3*81 are not perfect squares).

9.      Square of a negative number is always positive (-4*-4 = 16).

 

 

Squares of decimals and fractions can also be found.

 

Fraction

Decimal Number

Square of fraction

Square of decimal

2/3

 

4/9

 

1/10

.1

1/100

.01

6/10

.6

36/100

.36

12/10

1.2

144/100

1.44

2/100

.02

4/10000

.0004

 

Square roots:

We have seen that square of 3 is 9. We say that 3 is the square root of 9.

If n2  is the square of  a number n then n is the ‘square  root’ of  the number n2 . Square root is denoted by or  and is pronounced as “square root”.

 

Note:

Square root of a fraction = (square root of numerator/square root of denominator)

 = /

 

Square root of

= Number

 

=

 

 

=

=1.2

=.02

=5

 

 

1.2. Problem 1:  Find the two integers between which the square root of 147 lies?

 

Solution:

We know that 122=144 and 132=169

We also know that 144<147<169

 < <

 12  < < 13

 

1.2.1 Finding square root by factorisation

 

In this method we find all prime factors of the given number and then group the common factors in pairs.

If some factors do not appear in pairs then the number is not a perfect square and we stop the process of grouping.

 

1.2.1 Problem 1: Find the square root of

Solution:

By successive division we find that factors of 38025 are 5, 5,3,3,13,13

 38025 = 5*5*3*3*13*13 = 52*32*132 = (5*3*13)2

  = 5*3*13=195

By successive division we find that factors of 10404 are 2, 2,3,3,17,17

 10404 = 2*2*3*3*17*17 = 22*32*172 = (2*3*17)2

  = 2*3*17=102

=  =  =

 

1.2.1 Problem 2: Find the least number by which 2817 must be multiplied or divided to make it a perfect square.

 

Solution:

By successive division we find that factors of 2817 are  3,3,313.

 2817 =  3*3*313.

We note that the factor, 313 appears only once.

If we multiply 2817 by 313, then factors of (2817*313) are 3, 3, 313, 313 so that 2817*313= =3*3*313*313 = 32*3132 = (3*13)2

If we divide 2817 by 313 then factors of (2817/313) are 3, 3 so that 3617/313 =3*3 =  32

 

Therefore 313 is the smallest number which when multiplies or divides 2817 gives us the perfect square.

 

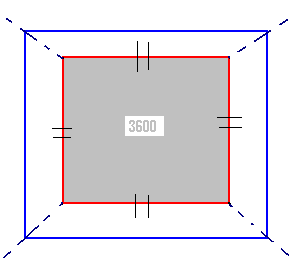
1.2.1 Problem 3: How much length of the wire is required to fence four rounds around a square garden whose area is 3600 sq.mts?

 

Solution:

 

In order to find the total length of wire required to fence the garden, we need to know its length and breadth.

We know that the area of the square garden = (length)2=3600

The factors of 3600 are  2,2,2,2,3,3,5,5

 3600 = 2*2*2*2*3*3*5*5 = 22*22*32*52=(2*2*3*5)2

  = 2*2*3*5=60

Therefore side of the square garden = 60 meters.

Perimeter of the square garden is sum of its 4 sides = 4*length of the square garden

 The length of wire required to fence the square garden = 240(=4*60) meters.

Since we need to fence four rounds around the square garden,

Total length of wire required = 4*perimeter = 4*240 = 960 meters

 

 

 

1.2 Summary of learning

 

 

No

Points studied

1

Perfect squares, finding square root by factorisation method

 

 

Additional Points:

 

 

Diagonal Method of finding squares (This is an ancient Indian method used for multiplication)

 

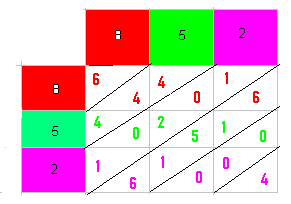
As an example let us find the square of the number 852:

Step 1: Write the digits 8, 5 and 2 both horizontally and vertically in a table as shown in adjacent Figure  Also write the product of each digit in the horizontal line with each digit in the vertical line in the appropriate box

 

 

8

5

2

8

64

40

16

5

40

25

10

2

16

10

04

 

 

 

 

 

 

 

 

 

 

 

Step 2: Diagonals are drawn across  all the boxes where product of digits are written (box containing 64, 40, 25…) as shown in the adjacent figure

Step 3: In each of the box write the unit’s number below the diagonal and the ten’s digit above the diagonal (In case of 40, write 4 above the diagonal and 0 below the diagonal). If the product of digits is a single digit number, write 0 above the diagonal and the single digit number below the diagonal (4 = 04)

 

 

Step 4 : Start adding numbers across the diagonals from the lowest diagonal, taking into consideration the carry from previous step if any, as follows:

 

Step

Diagonal

(see 2nd figure)

sum of the digits across diagonal

Carry from the previous step +

sum of the digits across diagonal

Carry

Unit

1

Lowest(4)

4

=none+4 =4

0

4

2

2nd lowest(0,0,0)=

0+0+0=0

=0+0 =0

0

0

3

3rd  lowest(6,1,5,1,6)

6+1+5+1+6=19

=0+19=19

1

9

4

4th lowest(1,0,2,0,1)

1+0+2+0+1=4

=1+4=5

0

5

5

5th lowest(4,4,4)

4+4+4=12

=0+12=12

1

2

6

Top most(6)

6

=1+6=7

 

7

 

The result is 725904 (Digits taken from the ‘Unit’ place in the above table)

 

This method holds good even for large numbers.

 

Properties of square roots:

 

1.      If the unit’s digit of a number is 2, 3, 7 or 8 then the number does not have a square root. The possible square roots in case of other numbers are as follows:

 

Units digits of square     ==è

0

1

4

5

6

9

Units digit of square root==è

0

1 or 9

2 or 8

5

4 or 6

3 or 7

 

2. The square root of an even square number is even and the square root of an odd square number is odd.

3. If the number ends with odd number of zeros then the number will not have an integer square root.

4. Negative numbers do not have  real square root number.

5. Square roots of a number can be positive or negative ( = 5).

 6. Square root of a rational number = Square root of numerator/Square root of denominator ( = / = 8/5)