4.1 Profit and loss:
1 Assume that you have a friend who is a
merchant who sells chocolate
and biscuits in addition to other items
1. He sells chocolate at 11Rs after buying them
at 10Rs
2. He sells biscuit packet at 23 Rs after buying
them at 20Rs
If he wants more profit from his sales, what
do you suggest him to sell more of chocolate or more biscuit packets?
2
A shop keeper buys 1000 coconuts
by paying Rs 6000. Of these 100 coconuts were spoiled. If he sells remaining
coconuts at Rs 5, did he incur loss or profit?
We shall learn to solve
these types of problems in this and subsequent lessons
4.1.1
Percentage:
You must have heard the
word percentage very often (% marks, % rate of interest, %pass in the board
examination…)
The word percent can be
split as per and cent
and means per 100
Definition:
‘Percentage’ is a fraction with denominator as 100 and is
represented by the symbol %.
Examples are
:
7% = 7 out of 100 =
7/100 = 0.07
0.025 = 0.025*100% = 2.5%
1/5 = 1/5*100% = 20%
100% means 100 out of
100
4.1.1 Example 1:
Let your marks in
mathematics be as given below:
1) In the first
monthly test it is 15 out of 25 ( 15/25)
2) In the Mid
term examination it is 65 out of 100(65/100)
3) In the third
monthly test it is 34 out of 50(34/50)
4) In the final
examination it is 105 out of 150( 105/150)
With the above data how can
we compare your progress in Mathematics in a year?
You must have thought why
not conduct examination for 100 marks always, so that comparison is easy. We
can use percentage calculation to measure the progress.
For calculating % we
convert the basis of comparison (denominator) to 100
Let us convert the basis of
comparison to 100 in case of above example
1. The marks scored in the
first test can be represented as
For 25, the marks is 15
For 100 how much? =
(15/25)*100 = 60
Thus the marks got in the
first monthly test is 60%
2. Since the mid term exam
is based on 100, conversion is not required and hence marks got is 65%
3. The marks in the third
monthly test can be represented as
For 50, the marks is 34
For 100 how much? =
(34/50)*100 = 68
Thus the marks got in the
first monthly test is 68%
4. The marks got in the in
the final examination can be represented as
For 150, the marks is 105
For 100 how much? =
(105/150)*100 = 35*2 = 70
Thus the marks got in the
final examination is 70%
We conclude that marks
scored in mathematics are 60%, 65%, 68% and 70%.
4.1.1 Problem 1:
An architect’s fees are worked out at 10% of the first Rs. 25,000 and 4% on the
reminder of cost. If the cost of house is Rs. 1, 50,000 find out
(1) Architect’s fee
(2) Express the architect’s
fee as % to the total cost
Solution :
The cost of house can be
split as25,000 and 1,50,000(1,50,000 = 25000+125000)
Since Architects fee are
different for different amount, we need to be calculate the fee separately on
25,000 and 125000
1. Architect’s fee on
25,000 is 10%
10% on 25,000 =
25000*10/100 = 2500
2. Architect’s fee on 1,25,000 is 4%
4 % on 125000= 125000
*4/100 = 5000
Total fee = 2500+5000 =
7500
For the total cost of house
of Rs. 1, 50,000 his fee is Rs 7500
For a cost of Rs 100 the
fee is =(7500/150000 )*100 =5
Thus we can say the
architect has charged a fee of 5% on the total cost
Verification:
5% of 150000 = (5/100)*
150000 = 7500, which is the fee charged by the architect and hence our answer
is correct
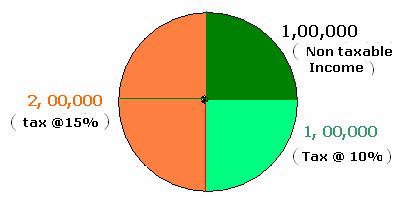
4.1.1 Problem 2:
Government of
|
1) Of
the total income, tax is not collected on the first Rs.1,00,000 2) On
the next 1 Lakh rate of tax is 10% 3) On
the rest of the income tax rate is 15% 4) In
addition, on the total tax collected it charges an educational cess(levy) of
2% Find
out the following for an individual whose income is Rs 4,00,000 (1)
Total tax paid by the individual (2)
Express the total tax as % to the total income |
|
Solution :
Total income = 4, 00,000
Non taxable income = 1,
00,000
Taxable income = 3,
00,000
Since the tax rates are
different for different amount, this taxable income needs to be split as 1,00,000 and 2,00,000. We also need to be calculate
tax separately on these two amounts.
1) On the first 1 Lakh the
tax is at 10%
10% Tax on 1,00,000 = 100000*10/100 = 10,000
2) On the next 2 Lakhs the
tax is at 15%
15% Tax on 2,00,000 = 200000*15/100 = 30,000
Thus the total Income tax
to be paid is 40,000(10,000+30,000)
In addition to tax am
educational cess of 2% has to be paid
2% cess on 40,000 = =
40000*2/100 = 800
Total tax payable is = I.Tax +cess = 40000+800 =
40800
On the total income
of Rs. 4, 00,000, tax is Rs 40800
On an income of Rs 100
the tax is = (40800/400000)*100 =10.2%
Thus we can say the tax
payable by this individual is 10.2%
Verification:
10.2% of 400000 =
(10.2/100)* 400000 = 40800, which is the total tax to be paid by the
individual.
4.1.1 Problem 3: The
population of a town is 24,000. If the number of males is increased by 6% and
that of females by 9%, the population would be 25,620 .
Find the number of females in the town.
Solution :
|
Let x
be the number of males in the town. Then 24,000-x will be number of
females Since the
increase in males is 6% , the increase in males = x*6/100 Since
the increase in females is 9% , the increase in females =
(24000-x)*9/100 Total
increase =
x*6/100 + (24000-x)*9/100 =6x/100+
240*9 -9x/100 = 2160-3x/100 The
total population = original population + increase = 24,000 + 2160-3x/100 This is
given to be 25,620 25620 =
26160 -3x/100 3x/100
= 26160-25620 (Add 3x/100 to both sides and subtract 25620 from both sides)
Thus
number of males are 18,000 and number of females is 6000 Verification: Since
the increase in males is 6%, the increase in number of males =
18000*6/100 = 1080 Since
the increase in females is 9%, the increase in number of females = 6000*9/100
= 540 Total
increase = 1080+540 = 1620 Thus
the total population = original population + increase = 24,000 + 1620= 25620,
which is as given in the problem. |
|
4.1.1 Problem 4: Divide
the sum of Rs 45,500 among three persons A,B, C in such a way that A gets
(33)1/3% more than B and C gets 60% of A and B together get.
Solution :
Let x be the
amount got B
Since A gets 33 1/3 % more
than B the amount got by A = amount got by B +(33)
1/3 % of B = x+ 33(1/3)x/100 = x+(1/3)x = 4x/3
The amount got by A and B
together = 4x/3+x = 7x/3
Since C gets 60% more than
what A and B got together,
Amount got by C= 60% of
(amount got by A and B together)
= (7x/3)*60/100 = 7x/5
The amount got by A+ amount
got by B and amount got by C = 4x/3+x+7x/5
= (20x+15x+21x)/15 (15 is
LCM of 3 and 5)
=56x/15
It is given that the total
amount distributed is 45,500
45500 = 56x/15
On simplification we get x
= 12187.5 which is the amount got by B
Amount got by
A = Amount got by B +(33) 1/3
% of B
= 12187.5 + 33(1/3)% of 12187.5 = 12187.5+ 4062.5 =16250
Amount got By A and B =
16250+12187.5 =28437.5
Amount got by
C= 60% of (amount got by A and B together)
= .6*28437.5 = 17062.5
Verification:
Check the following:
1. 16250 is (33)(1/3)% more than 12187.5
2. 17062.5 is 60% of
(12187.5+16250)
4.1.2
Profit and Loss
You must have been to
provision stores to buy daily requirements. The merchant sells items at a price
to you after he buys same from the market or a producer of items.
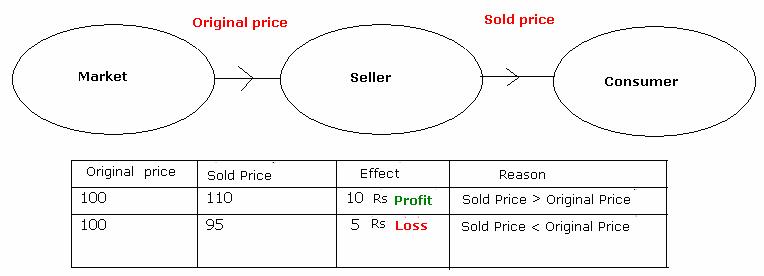
The price at which the item
is sold is called ‘selling price(SP)’.
In order to sell items to you, he has to buy these items from some one, may be
from a producer or from another merchant.
The price at which the item
is purchased is called ‘Cost price(CP)’
The merchant has his own
expenses (He pays rent for the shop, pays for electricity bills, and pays
salary to employees…). For this reason the seller has to sell items at a price
more than the price at which he has bought the items.
The extra money he gets is
difference between selling price and cost price. It is called profit.
Profit = SP-CP (
SP>CP)
There can be situations
where a merchant wants to get rid of old stock of items. In such cases, he may
sell items at a price less than the purchase price. In such cases he incurs
loss.
Loss = CP-SP ( SP<CP)
Though we may buy items in
smaller quantities from the merchant, the merchant always purchases items in
large quantities.
Since the merchant buys in
large quantities he gets some reduction in prices from the first (original)
supplier.
The price at which goods
are bought or sold on a large scale is called ‘Wholesale
price’
The price at which goods
are bought or sold on a small scale is called ‘Retail
price’
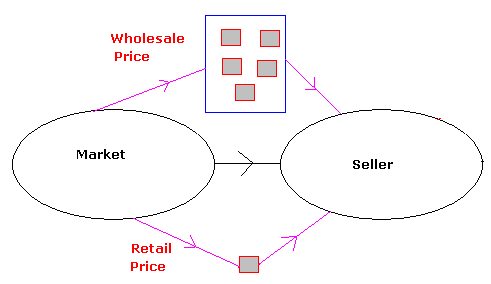
Whole sale
price is always < Retail Price.
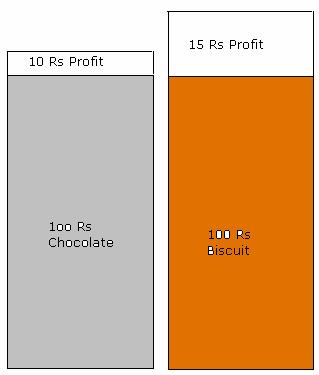
Suppose a shop owner is a
friend of yours. Apart from selling other items assume he sells chocolates and
biscuits as follows:
1. He sells a bar of
chocolate at 11 Rupees which was purchased by him at 10 Rupees
2. He sells a packet of
biscuits at 23 Rupees which was purchased by him at 20 Rupees
He wants to make more
profit. For that, he is not sure whether he should sell more biscuits or more
chocolates. Since you are a student of
mathematics he wants your advice!. What will you
suggest to sell more chocolates or more biscuits?
|
In the
first case for every chocolate of 10Rs, he got a profit of 1Rs. So, for
chocolates of 100 Rs (=10Chcokolate bars) his
profit was 10Rs(=10*1) In the
second case for every biscuit pack of 20Rs, he got a profit of 3Rs. So, for
biscuits of 100 Rs (=5 packs) his profit was 15 Rs (=5*3) So, for
same amount of sale (=100 Rs), he gets 5
Rs(=15-10) extra if he sells biscuit packs. Thus it
is profitable to sell more biscuits than chocolates. |
|
What did we do? In both the
case we arrived at his profit on sale of 100Rs (%) to Cost Price (CP).
The ‘profit percentage’ is the profit made on a Cost
price of 100Rs.
There could be losses on
sales also
The ‘loss percentage’ is the loss made
on a Cost price of 100Rs.
The formulas used for
various calculations are:
Profit = SP-CP
Loss = CP-SP
Profit % = Profit*100/C.P.
Loss % = Loss*100/C.P.
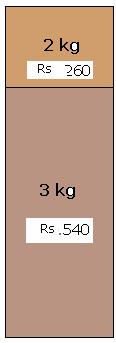
4.1.2 Problem 1: A grocer mixed 3 kg of tea powder at Rs 180Rs
per kg with 2kg of tea powder at Rs.130 per kg. If he sells
the mixture of two at Rs 192 per kg. Did he make profit or loss and what
is the percentage?
Solution :
|
1. Cost
of 3kg tea powder @180 Rs = 3*180*3 = Rs 540 2. Cost
of 2kg tea powder @130 Rs = 2*130*2 = Rs 260 Total
cost of tea powder = Rs 800 By
mixing tea powders he will have total of 5 kg of tea powder. His
sale price of 5kg at Rs 192
= 192*5 = Rs. 960 Since
SP > CP, he has made a profit
|
|
4.1.2 Problem 2: A coconut seller purchased 1000 coconuts for
Rs.6000. Unfortunately 100 coconuts were rotten. He sold remaining coconuts at Rs each. Find the
profit %.
Solution :
Since 100 coconuts were
rotten the seller was left with only 900 coconuts.
The money he got by
selling 900 coconuts at Rs.5 = 900*5 = 4500
Since SP> CP he has made
a loss = CP-SP =6000-4500 = 1500.
Loss % = Loss*100/C.P.=
1500*100/6000 = 25%
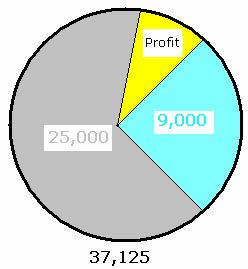
4.1.2 Problem 3 : A shop keeper makes a business of Rs 37,125 in
a month. He spends Rs 25,000 for purchase of items. He pays Rs 9000 towards
rent, salary to employees and other expenses. Find the profit or loss percentage
Solution :
|
His
expenses (equivalent to CP) are Rs 34,000(=25,000+9000) His
income (equivalent to SP) = 37,125 Since
SP>CP, he has a made a profit of SP-CP= 37,125-34,000 = 3125
|
|
If we are given selling price(SP) and profit or loss % , we can find cost price by
the formula
CP = 100*SP/(100+Profit%) when there is a profit
CP = 100*SP/(100-Loss%) when there is a
loss
4.1.2 Problem 4: A fruit seller cuts a papaya into 12pieces
and sells each piece at Rs 2.50.If he gains 50% find the cost price of papaya
fruit
Solution :
|
Since
Papaya fruit is cut in to 12 pieces and selling price of each is Rs 2.50 Selling
price of papaya(SP) = 2.50*12 = Rs 30. His
profit% is given as 50. We are required to find CP Since
he has made a profit of 50% CP = 100*SP/(100+Profit%) = 100*30/(100+50) =
100*30/150 = 20 Rs Veification: SP =30
and CP=20
|
|
4.1.2 Problem 5:
If a vegetable
vendor sells 10 Kg of beans at Rs71.25 and incurs a loss of 5%, What is his cost price?
Solution :
Since he has made loss of
5%
CP = 100*SP/(100-Loss%) = 100*71.25/(100-5) = 100*71.25/95 = 75Rs
Veification:
SP =71.25 and CP=75
Loss = CP-SP =
75-71.25 = 3.75 Rs
Loss % = Loss*100/C.P =
3.75*100/75 = 5% which is the loss% as given.
If we are given Cost price(CP) and profit or loss % , we can find List price by the formula
SP = (100+Profit %)*CP/100
when there is a profit.
SP = (100-Loss %)*CP/100
when there is a loss.
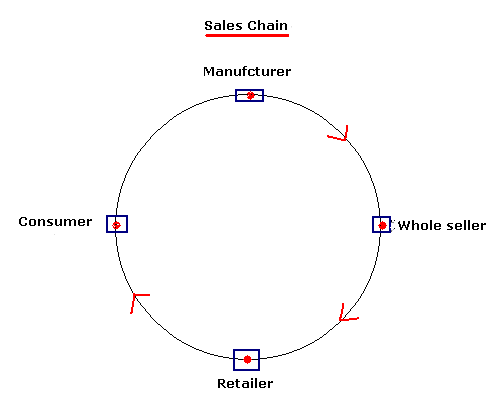
4.1.2 Problem 6: Let us understand how an item manufactured by
a manufacturer reaches a buyer. Firstly, the item is manufactured by a
manufacturer. Then, the manufacturer sells the items to a Wholesale merchant.
Then the wholesale merchant sells the
items to retailers. Finally retailer sells the item to Buyer.
|
|
A manufacturer gains 50% on
each item when an item is sold to a wholesale merchant. Wholesale merchant
gains 25% on each item sold to retailer. Retailer gains 10% on each item sold
to a buyer. If cost of manufacturing an item is Rs 200. Find out the price paid by an
individual.
Solution :
We need to find SP of an
item by Manufacturer, Wholesale Merchant and Retailer.
Since each one is making a
profit we need to use the formula: SP = (100+Profit %)*CP/100
SP of a manufacturer =
(100+50)*200/100 = 300Rs ( CP of a Manufacturer is 200)
SP of a Wholesale merchant
= (100+25)*300/100 = 375Rs ( CP of a Wholesale merchant is 300)
SP of a Retailer =
(100+10)*375/100 = 412.50 Rs ( CP of a Retailer is 375)
Veification:
Let us find gain for Manufacturer ,Wholesale merchant,Retailer:
For Retailer SP =412.50 and
CP=375
Profit = SP-CP =
412.50-375 = 37.5
Profit % =
Profit*100/C.P = 37.5*100/375 = 10% which is the gain as given.
For Wholesale merchant SP =375 and
CP=300
Profit = SP-CP =
375-300 = 75
Profit % =
Profit*100/C.P = 75*100/300 = 25% which is the gain as given.
For Manufacturer SP =300 and CP=200
Profit = SP-CP =
300-200 = 100
Profit % =
Profit*100/C.P = 100*100/200 = 50% which is the gain as given.
4.1.2 Problem 7: By selling an article for Rs 23 a man lost 8%.
At what price should he sell it to make a profit of 10%?.
What is the cost price of the article?
First we need to calculate
CP and then find SP
Solution :
Since man has lost 8% by
selling at Rs 23.
CP = 100*SP/(100-Loss%) = 100*23/(100-8) = 100*23/92 = Rs 25
Since he has to make a
profit of 10% on a CP of Rs 25
SP = (100+Profit %)*CP/100 =
(100+10)*25/100 = 110*25/100 = Rs.27.5
Veification:
When the man sold at a loss
CP =25, SP =23: loss =
CP-SP = 25-23 =2
Loss % = Loss*100/C.P = 2*100/25 = 8% which is
the loss% as given when he sold the article at Rs.23
When he makes a profit
SP=27.5(as Arrived at above) and CP is still =Rs25
he
has made a profit = SP-CP = 27.5-25 = 2.5
Profit % =
Profit*100/C.P= 2.5*100/25 =10% which is as given
4.1.2 Problem 8: A merchant purchased 1000 cucumbers for Rs.3800.He
paid 2% tax and spent Rs.50 on transportation.40 of them were spoiled. At what
price should he sell the remaining to gain Rs.1114 on the whole?
Solution :
Since we want to know his
SP, first we need to calculate the CP. The CP should include his purchase
price, tax and transportation.
Purchase price of 1000
cucumbers = 3800
Tax at 2% on RS 3800 =
3800*2/100 = 76
Transportation cost = 50
Total CP =
3926
SP = CP+ profit = 3926+1114
= 5040
Since 40 cucumbers were
spoilt he could sell only 960
His rate of sale of
cucumber = 5040/960 =
Rs 5.25
Veification:
SP = no of cucumbers * rate = 960*5.25 =
5040
Profit = SP-CP = 5040-3926
= 1114 which is as given in the Problem
4.1Summary
of learning
|
No |
Points to remember |
|
1 |
Profit
= CP-SP (When SP>CP) |
|
2 |
Loss =
SP-CP (When SP<CP) |
|
3 |
Profit
% = Profit*100/C.P |
|
4 |
Loss %
= Loss*100/C.P |
|
5 |
CP =
100*SP/(100+Profit%) (when there is a profit) |
|
6 |
CP =
100*SP/(100-Loss%) (when there is a loss) |
|
7 |
SP =
(100+Profit %)*CP/100 (when there is a
profit) |
|
8 |
SP =
(100-Loss %)*CP/100 (when there is
a loss) |
Additional Points:
4.1.2 Problem 9:
A man sells a TV set for Rs 6900 and makes a profit of 15%. He sells a second
set at a loss of 10%. If on the whole he neither gains nor loses, find the cost
price of the second TV set.
Solution:
SP = 6900. Profit% = 15
We know CP = 100*SP/(100+Profit%). By substituting values we get,
CP = 100*6900/115
= 6000
We also know that Profit =
CP-SP and hence
Profit = 6900-6000 = 900
Since in all he does not
make any profit or loss, it is clear that he incurs a loss of Rs 900 while
selling the second set.
We know
Loss % = Loss*100/C.P
Therefore
10 = 900*100/CP
And hence CP = 9000
Thus the cost price of
second TV set is Rs 9000.
4.1.2 Problem 10: A man bought two transistors which costed him Rs 720. He sold one of
them at a loss of 15% and the other at a gain of 19%. If the selling price of
both transistors is same find the cost price of each transistor.
Solution:
Let x be the cost price of
first transistor.
The cost price of
second transistor is 720-x.
When sold at a loss we know
SP = (100-Loss
%)*CP/100
SP
= (100-15)*x/100 = 85x/100
Since the 2nd transistor
was sold at profit we know
SP = (100+Profit
%)*CP/100
SP
= (100+19)*(720-x)/100 = 119*(720-x)/100
Since SP of both
transistors is same, we have
85x/100
= 119*(720-x)/100
i.e. 85x = 119(720-x) = 119*720 - 119x
i.e. 85x+119x = 119*720
i.e. 204x = 119*720
x = 119*720/204 = Rs 420
which is the cost price of first transistor
The CP of second
transistor = 720-x = 720-420 = Rs 300
Verify that above working is correct.