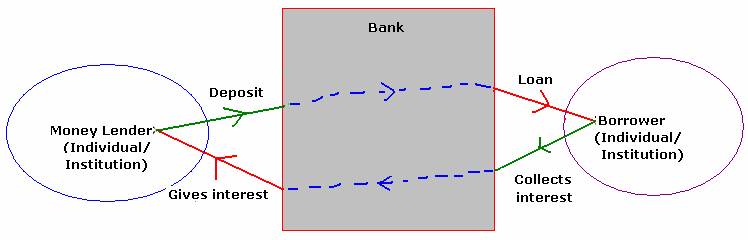
4.5 Simple Interest:
The money given by a
depositor to Bank or the money given by bank to a borrower is called ‘PRINCIPAL’ Amount.
The duration for which money
given by depositor to the Bank or the duration for which money is taken on loan
from bank is called ‘PERIOD or TERM’ The
interest one gets from bank or the interest charged by a Bank on a loan is
normally expressed as a % for an year. Since Banks also have to make profit after paying
for expenses ( rent for the building,
salary to its employees printing of stationary, electricity and other
expenses). Bank’s major income comes from interest charged on loans. They also pay interest to depositors. Thus, in order that Banks are profitable they
charge more interest on loans (around 5% more) when compared to interest given
on deposits.
|
|
4.5 Example 1:Ram
has deposited 5000Rs in State Bank of
What does 8% interest mean
to Ram? (The bank agrees to pay 8 Rupees for every 100 Rupees every year)
It is given that for Rs.
100 he gets 8 Rs per year (8% interest)
For Rs. 5000 he gets
8*5000/100 = 400Rs per year
Since he has deposited
Rs.5000, he should get Rs.400 every year for 6 years
In all he will get Rs.2400
(=400*6) as interest in 6 years from Bank
He will also get back his
principal amount of 5000Rs at the end of 6 years
In banking terms this
method of arriving interest is called ‘Simple Interest’
If
P = Principal amount (The
sum borrowed or the sum lent)
N = Period (Term) of
Deposit/loan in
years
R = Rate of Interest (The
interest amount on every Rs 100 for one year)
I = The
interest money paid by borrower to the money lender or to the bank for use of
money (P) borrowed
A =The amount paid/payable
at the end of period then(A = P+I )
For simple Interest
calculation we use the formula:
Simple Interest
(SI)= (P*N*R)/100
Let us verify correctness
of our interest calculation in the
above example using the above formula
Verification:
P = 5000
N= 6years
R = 8%
Substituting these values
in the above formula we get
Interest = (P*N*R)/100
= (5000*6*8)/100 = 50*6*008
=2400 which is what we arrived in the example
Since A = P+I and I =
P*N*R/100
A = P+ (P*N*R)/100 = P{1+ (N*R)/100}
For easy calculation of
interest, Bank employees use a table
called ‘Ready Reckoner’ (Pre calculated table of interest for
different amount and interest rates) for
calculating simple interest. It is a table showing interest amount for one
month or for one day for different ‘Principal’ amounts.
Sample Ready Reckoner for
interest for One Month is given below:
|
Principal(Rs.) |
Rate@
4% Per
Annum |
|
1 |
.0033 |
|
2 |
.0067 |
|
... |
….. |
|
10 |
.0333 |
|
20 |
.0667 |
|
30 |
.1000 |
|
40 |
.1333 |
|
50 |
.1667 |
|
100 |
.3333 |
|
200 |
.6667 |
|
300 |
1.0000 |
|
400 |
1.3333 |
|
500 |
1.6667 |
|
1000 |
3.3333 |
|
... |
….. |
4.5 Problem 1: Calculate
simple interest for Rs 550 at 4% for 4 months using the above Ready Reckoner
Solution :
Step 1. 550 = 500+50
(split the principal so as to use the table easily)
Step 2: Interest for one
month for Rs 500 = 1.6667
Interest for one month for Rs.50 = .1667
Step 3 :
interest for one month for Rs 550 = 1.
8334(=1.6667+.1667)
Step 4 :
interest for 4 months = (1.8334)*4 = 7.3336
Activity :
Visit a Bank and ask for a Ready Reckoner. You will notice that Interest is tabulated for the
principal amount from Rs 1 to 9 and then from 10 in multiples of 10 up to 50 and then multiples of 100 up to 500
and then multiple 1000 up to 5000 and so
on.
Did you ever think why it
is so? The reason is that any amount can be split among small numbers appearing
in the Ready Reckoner table
For example, 6047 =
5000+1000+40+7 and hence interest on 6047 is same as sum of interest on the
split amounts of 5000,1000,40,7
Note:
As per the
above ready Reckoner, For Rs.100 the interest at the rate of 4% is0.3333.
However, can we not calculate the interest on 100 in another way as (Interest
on Rs.1*100)= .0033*100=.3300. Notice the difference
in interest between two methods which is .0033. This is because, the calculation
of interest is done only up to 4
decimal places and hence a rounding error. If the amount deposited is very
large, the interest difference will be huge. Because of this reason, the person
who uses Ready Reckoner has to be careful.
Let us take the case of
borrower.
4.5 Problem 2: Mr. Raj borrows from State Bank
of
Solution :
In this case we have
P = 150000
R= 12
N =7
Substituting these values
in the formula we get
Total interest =
150000*7*(12/100) = 1500*7*12 = 126000
Since he also pays
principal loan amount at the end, his
total payment to bank will be Rs 2,76,000(=1,50,000as principal +1,26,000 as
Interest)
4.5 Problem 3: A sum of money amounts to Rs 3,360
at 14% Simple interest in 3 years. Find the interest on the same sum for 3 1/2
months at 6%
Solution :
In this case we have
A = 3360, R =14 and N=3
But A = P{1+ (N*R)/100}
3360 = P{1+ (3*14)/100} = p*142/100
![]() P = 3360*100/142 = 2366
P = 3360*100/142 = 2366
R = 6 and N = 3 1/2 months= 3.5/12 years
SI = (P*N*R)/100=
{2366*(3.5/12)*6/100} = Rs. 41.41
4.5 Problem 4:
Three sisters are 5, 10 and 15 years old. Their father leaves Rs80,250 in a bank; paying 5% simple interest. If each gets the
same amount at the age of 20, find their shares at the time of father’s death.
Solution :
Since each of the sister get the amount
at the age of 20 years. Let the sister’s share be P1,P2 and P3 respectively
First sister’s share (P1)
is held in the bank for 15 years
Second sister’s share (P2)
is held in the bank for 10 years
Third sister’s share (P3)
is held in the bank for 5 years
The amount got by first
sister after 15 years
= P1{1+ (N*R)/100}= P1{1+
(15*5)/100} =1.75 P1
The amount got by second
sister after 10 years
= P2 {1+
(N*R)/100}= P2 {1+
(10*5)/100} =1.5 P2
The amount got by third
sister after 5 years
= P3{1+ (N*R)/100}= P3{1+
(5*5)/100} =1.25 P3
Since it is given that the
amount they get at the age of 20 years is same
1.75 P1=1.5 P2=1.25
P3
On simplification we get
7P1=6P2=5P3
![]() P2
= 7/6P1
P2
= 7/6P1
and P3 =
7/5P1
But it is given that P1+P2+P3
= 80250
![]() P1+7/6P1+7/5P1=
80250
P1+7/6P1+7/5P1=
80250
I.e. (30+35+42)/30 P1=
80250
I.e. P1=
80250*30/107 = 22500
By substituting this value
we find that
P2 = 7/6P1=
26250
P3 = 7/5P1=
31500
The sisters share at the
time of their father’s death is Rs 22,500, Rs26,250
and Rs,31,500.
Verify using the
formula that these deposits fetch same amount when the sisters attain the age
of 20 years.
4.5
Summary of learning
|
No |
Points to remember |
|
1 |
Simple Interest (SI)= P*N*(R/100)
Where P =
Principal Amount N = Period (Term) of Deposit: R = Rate of Interest |