5.1. Introduction to Statistics:

Introduction:

1. What will be the population of India in 2005,2010?

2. What is the literacy rate of india and its states?

3. What is the % of kids not attending to school. What will be status in next 10/15 years?

4. What is the deviation in salary among people working in an organization?

Statistics a branch of Mathematics helps to find answers to these types of questions.

In our daily life we come across news about average rainfall in a place, Minimum and maximum temperatures in a place, average runs scored by a cricketer, average attendance and similar terms. They are all calculated based on data. They are useful for planning by agencies such as Government, for comparing performance of people and for other purposes.

You must have heard people saying that a month of current year has been very hot. This observation is normally based on their feeling. However this feeling can be checked by correct data. The Metrological department has many recording stations where they measure the minimum and maximum temperatures daily.

Let us tabulate the maximum and minimum temperatures of a city in north India.

Month	January	February	March	April	May	June	July	August	September	October	November	December
Maximum (Mid Day)	15	14	20	18	35	36	40	41	35	30	25	22
Minimum (Early Morning)	6	7	10	10	20	22	24	25	22	20	15	-5

From the above data it is difficult to guess the temperature in the middle of any month in a year. Let us see what if we represent the above data in a graph:

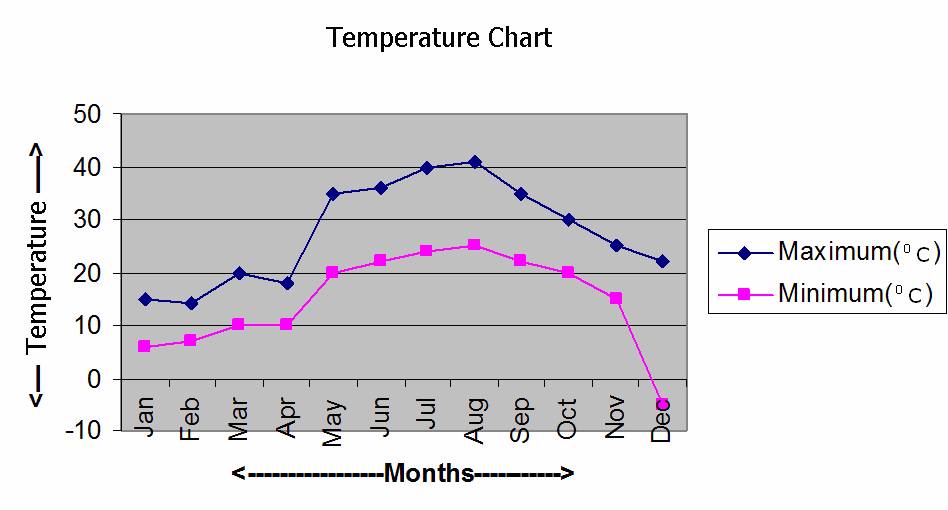
Graphs

The above pictorial representation is recording of Maximum and minimum temperatures of a place for the Months of January to December (lowest and highest among any days in those months) of a year. Blue color line represents the Maximum temperature and pink color line represents the minimum temperature. This plotting has been done based on the following data:

Table:

Monthsà	Jan	Feb	Mar	Apr	May	Jun	Jul	Aug	Sep	Oct	Nov	Dec
Maximum(^0C)	15	14	20	18	35	36	40	41	35	30	25	22
Minimum(^0C)	6	7	10	10	20	22	24	25	22	20	15	-5

Looking at the data in the above table, isn’t it difficult to estimate the temperature in the middle of any month?

Don’t you agree that pictorial representation (called Graph) is much easier to understand compared to the data given in the above table?

Isn’t there a saying that a picture represents more than what thousand words say?

Let us understand how this graph has been plotted.

On the horizontal line we see names of months. Each month is separated by a gap of around 1cm in length and we say that the horizontal scale is 1cm = 1month. On the vertical line we see markings in steps of 10 starting with -10 ( i.e.-10,0,10,20,30,40,50). We notice that the distance between two markings on vertical line is approximately 1cm and we say that the vertical scale is 1cm = 10⁰C. Since we do not have temperatures recorded in excess of 50⁰C, the markings have been stopped at 50⁰C. Since we do not have minimum temperatures recorded below -10⁰C, the markings haven’t been provided for -20⁰C and below that. Though in this example the scale for horizontal and vertical lines is same, they need not be same always. Here we used the scale of 1cm. Scale is determined in such a way that all data can be marked on the sheet.

Note that from the graph it is possible to estimate easily the minimum and maximum temperature during middle of any month which is not possible to arrive at easily by looking at data in the table.

In case of geographical map, you must have observed that the scale used for distance as 1cm =1000Km.

By convention we call the horizontal line as x axis and vertical line as y axis. Any point in a plane(surface) is represented by coordinates(x, y).

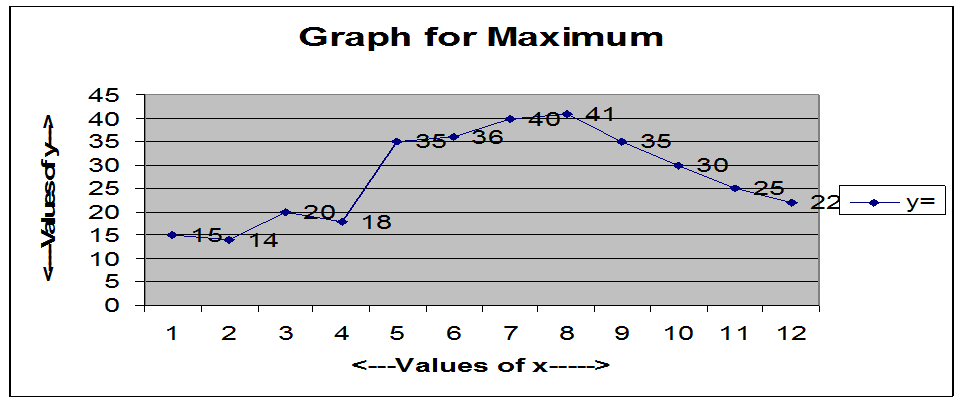
5.1.1 Example 1: Draw a graph for maximum temperatures based on the above table. Horizontal line(x axis) will represent months and vertical line(y axis) will represent maximum temperatures. The months are represented from 1 to 12 for January to December. Then the coordinates are:

x à	1	2	3	4	5	6	7	8	9	10	11	12
y à	15	14	20	18	35	36	40	41	35	30	25	22
(x, y)à	(1,15)	(2,14)	(3,20)	(4,18)	(5,35)	(6,36)	(7,40)	(8,41)	(9,35)	(10,30)	(11,25)	(12,22)

For marking temperatures we can use the scale 1cm = 5⁰C and start marking from 0⁰C, in multiples of 5(0,5,10,15..). After marking the points (x,y) and joining them, we get a graph as shown below.

5.1.1 Example 2: Assume that you have collected the following data of time taken to run 100 Meters race in your school games for the years 2000,2001,2002,2003 and 2004 (First 3 places only).

No	Name	Class	Year	Time taken to run 100Meters race
1	Ram	8	2000	15sec
2	John	9	2000	16sec
3	Krish	10	2000	17sec
4	Luis	9	2001	12sec
5	Sham	8	2001	17sec
6	Gopal	9	2001	19sec
7	Ahmed M	9	2002	13sec
8	Khan A K	8	2002	16sec
9	Arun	10	2002	17sec
10	Mohan	10	2003	16sec
11	Philips	8	2003	17sec
12	Ajay	9	2003	18sec
13	Pramod	9	2004	14sec
14	Raymond A	8	2004	15sec
15	Gopi	9	2004	15sec

Let us consider only those data corresponding to the time taken by students for running the race. We have 15,16,17,12,17,19,13,16,17,16,17,18,14,15,15 secs.

Since the above data is not in any particular order, let us arrange them in ascending order. We get

12, 13, 14, 15, 15, 15, 16, 16, 16, 17, 17, 17, 17, 18, 19..

No	Time (sec)	Occurrence(Frequency)
1	12	1
2	13	1
3	14	1
4	15	3
5	16	3
6	17	4
7	18	1
8	19	1
Total		=15(Total No of Scores)

The above representation of data called ungrouped frequency distribution table.

From the above tabulation we observe the following:

1. Lowest time taken is 12 Seconds which happened in the year 2001.

2. Highest time taken is 19 Seconds (among first 3 winners) which happened in the year 2001.

3. The number 17 has highest occurrence of 4, indicating that most of the prize winners took 17 Seconds to run the distance.

Let us regroup the data as follows:

No	Grouping (Class-Interval)	Occurrence(Frequency)
1	12sec -14sec	3
2	15sec-17sec	10
3	18sec -20sec	2
Total		=15(Total No of Scores)

The above representation of data is called grouped frequency distribution table.

When scores (data) are large in number, grouped frequency distribution tables are very easy for analysis.

If we group students into 3-Second time intervals {i.e. (12-14),(15-17),(18-20)} we find the interval of (15sec-17sec) has the highest occurrence of 10, indicating that most of the prize winners took between 15 to 17 seconds to run the distance. We also notice that if we group results in different time intervals the conclusion will be different.

5.1.2 Statistical terms

The numbers we have collected are called ‘Scores (observations)’. The number of times a particular score occurs is called ‘Frequency’. Some times we group the scores in ranges (intervals) for meaningful analysis and such sub groups are called ‘Class-intervals’. This class interval is never fixed and can vary. Based on the class interval chosen, the conclusion could change. (In the above example we can choose class intervals of 4 -Seconds(ex 12sec-15sec,16sec-19sec).Once a class interval is chosen all data has to be grouped as per this grouping (i.e. in the above example we can not have 2-second intervals and 3-second intervals at the same time).The difference between the highest and the lowest values of the scores(data) is called ‘range of data’. The difference between lower and upper limits of two consecutive classes is called ‘size of the class’

Thus ‘Statistics’ could be defined as science of collection, classification, analysis and interpretation of basic numerical data. It finds applications in prediction of economic growth of a country, weather pattern of a region, etc. These scientific predications help Government and Agencies to plan for future. Statistics is used in Genetics, Biological sciences, Education, Medicine, Economics.

5.1 Summary of learning

No	Points to remember
1	The numerical figures collected for analysis are called scores
2	The number of times a score repeats itself is called frequency
3	The data arranged in the format of a table containing the score and its frequency is called frequency distribution table.
4	Grouping of scores in to smaller groups is called class interval.