1.10
Probability(Part 1)
Introduction:
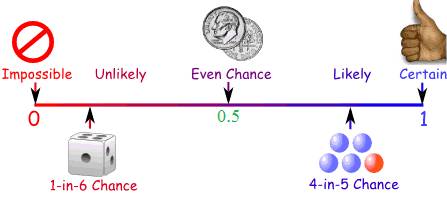
The above picture summarises chances of
some thing happening from 'impossible' to 'possible'.
As we know
‘probability’ means chance of some thing happening. It could be any of the
following:
1. The chances
of rains on any particular day
2. The
chances of
3. A
cricketer scoring century in a particular test match
4.
5. Number
of times head comes up when 1 rupee coin is tossed up 100 times
6. Number
of times number 2 appears when a dice is
drawn 500 times
The outcome of any of the above event is pure chances. It
may happen or it may not happen. Do you notice the difference between first 4 statements and the last 2
statements? In case of first 4 cases, the result depends upon external factors
such as place, time, strength of opposition team.. where as result of 5 and
6 will almost be same irrespective of
place and time of the event. There are
cases when outcome of certain events can be forecast with some certainty. One
such event is tossing of coin. When we toss the coin there can only be 2
outcomes, either head appears or tail appears. When coin is tossed up several
times obviously, the chances of head coming up can vary from 0% to 100% and
tail coming up can vary from 100% to 0%. However when coin is tossed up in large number of times(in
thousands) head coming up may be 50% and
tail coming up could be 50%.

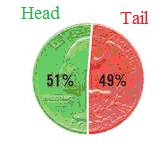
In such cases, the
probability is 1/2. Note that when head appears tail can not appear at the same
time. Similarly when tail appears, head can not appear at the same time.
This we say that events are exclusive.
That is to say, there can not be any other possibility other than head
appearing or tail appearing. In such case, we note that the sum of their
probability is 1/2+1/2= 1. Note that probability is
expressed as a ratio and it is always ≤
1. why does dice have dots numbers from 1 to 6?.

Note that dice is a
cube and it has 6 faces. Hence their faces are represented by 1 to 6 dots
representing numbers from 1 to 6. When a dice is cast what are the chances of a
number appearing from 1 to 6? It is one out of 6 and hence the probability is
1/6.
What is the sum of
probabilities of number appearing between 1 and 6?
It is = Probability
of number 1 appearing+ Probability of number 2 appearing + Probability of
number 3 appearing + Probability of number 4 appearing + Probability of number
5 appearing + Probability of number
appearing between 1 and 6
= 1/6+1/6+1/6+1/6+1/6+1/6=
1
(Note that, when
one number appears when a die is cast, other number can not appear at the same
time. Since probability of each number appearing is excusive of others, sum of
their probabilities is equal to 1.
Probability of number
1 not appearing
= Probability of
number 2 appearing + Probability of number 3 appearing + Probability of number
4 appearing + Probability of number 5 appearing + Probability of number 6
appearing = 1/6+1/6+1/6+1/6+1/6= 5/6
This also can be
calculated as
Probability of
number 1 not appearing = 1 - Probability of number 1 appearing = 1-1/6= 5/6
Let us learn some
of the definitions of terms used
|
No |
Term |
Meaning |
Examples |
|
1 |
Experiment |
Test
or a procedure or operation which produces a result. In this lesson all
experiments will be random. |
|
|
2 |
Trial |
Performing
an experiment |
tossing
a coin/throwing a dice |
|
3 |
outcome |
Result
of trial |
head
or tail/ appearance of number from 1 to 6. |
|
4 |
Sample
space |
Set
of all possible outcomes |
S
= {H,T}. S = {1,2,3,4,5,6} |
|
|
Event |
Every subset of
Sample Space |
Getting
the head=A= {H}, Getting
the number 4=B={4} Getting
even numbers= B = {2,4,6} |
|
5 |
Elementary
event |
Each
of the outcome in sample space. That is
each of the element in sample space. (Every subset of sample space
having only one element) |
Getting
the head=A= {H}, Getting
the number 4=B={4} |
|
Experiment |
Sample
space and Events |
No
of events n(S) |
Event
A |
Favourable
outcomes to event A and n(A) |
Probability P(A) =
n(A)/n(S) |
|
1
coin is tossed |
S={ H,T } |
2 |
Tail
coming up |
A=(T) n(A)=1 |
1/2 |
|
2
coins are tossed |
S={ HH,HT,TH,TT } |
2*2=4 |
Tail
should not come up |
A
= {(HH)} n(A)=1 |
1/4 |
|
3
coins are tossed |
S={ HHH,HHT,HTH,THH,
HTT, THT,TTH,TTT } |
2*2*2=8 |
Same
face coming up |
A=
{(HHH),(TTT)} n(A)=
2 |
2/8 |
|
1
dice is cast |
S={1,2,3,4,5,6 } |
6 |
Even
number coming up |
A={2,4,6} n(A)=
3 |
3/6 |
|
2
dices are cast |
S={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6) (2,1),(2,2),(2,3),(2,4),(2,5),(2,6) (3,1),(3,2),(3,3),(3,4),(3,5),(3,6) (4,1),(4,2),(4,3),(4,4),(4,5),(4,6) (5,1),(5,2),(5,3),(5,4),(5,5),(5,6) (6,1),(6,2),(6,3),(6,4),(6,5),(6,6) } |
6*6=36 |
Getting the same number |
A=
{(1,1),(2,2),(3,3), (4,4),(5,5),(6,6) n(A)=
6 |
6/36 |
P(E) =
Probability of an event ‘E’ = ![]() =
=![]()
Observe that P(A)+
P(![]() ) =1 (
) =1 ( ![]() n(A)/n(S) + n(
n(A)/n(S) + n(![]() )/n(S) ={ n(A) + n(
)/n(S) ={ n(A) + n(![]() )}/n(S) = n(S)/ n(S)
)
)}/n(S) = n(S)/ n(S)
)
![]() P(A)
=1- P(
P(A)
=1- P(![]() ), P(
), P(![]() ) =1- P(A)
) =1- P(A)
Probability:
It is the ratio of the number of elementary elements favourable to the event E
to the total number of elements in the sample space
Can probability ratio be 0 or 1?
1. What is the probability of getting a number 0 or greater than 6 when dice is cast?
In this case A = {} an empty
set, and n(S) = 6 , hence P(A)= n(A)/n(S)= 0 (When a dice is cast number is one among 1 to 6 only). This we call an impossible event,
because such a event does not happen
2. What is the probability of getting a number 1 to 6 when dice is cast?
In this case A = S and hence n(A) = n(S) = 6 , Thus P(A)= n(A)/n(S)= 1 (When a dice is cast number is always one among 1 to 6). This we call a sure event, because such a event always happens
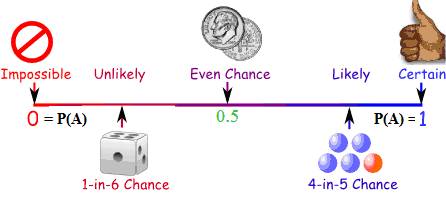
Thus 0 ≤ P(A) ≤
1 This is what we represented in the beginning by a figure:
Problem
1 :
A survey of 850 working woman showed that 158 used own four-wheeler, 416 used
two-wheeler, and the remaining used public transport. If one is chosen randomly
among these women, what is the probability of the woman who commute by (1) own
four wheeler (ii) Own two wheeler (iii) public transport and (iv) own vehicles.
Solution:
Number of women
travelling by their own vehicles= 158+416= 574
Number of women
travelling by public transport= 850-574= 276
Probability of
woman using own four wheeler = 158/850
Probability of
woman using own two wheeler = 416/850
Probability of
woman using public transport = 276/850
Probability of
woman using own vehicle = 574/850=
(158/850+416/850)
Problem
2 :
A box contains 12 balls out of which 'x'
are red.
(i) If one ball is drawn, what is the probability of getting
red ball?
(ii) If 6 more red
balls are put in the box, the probability of a drawing a red ball will be
doubled than earlier. Find 'x'
Solution:
(i)
Since 'x' number of balls are red out
of total of 12 balls, the probability of
getting red is x/12
(ii)
When 6 more
balls are added, total number of balls become 18 (=12+6)
Hence the new
probability of getting a red ball =
(x+6)/18
It is also given
that new probability is twice the earlier probability thus New probability =
2x/12= x/6;
![]() (x+6)/18 = x/6
(x+6)/18 = x/6
6x+36=18x
36= 12x
x=3
1.1 Summary of learning
|
No |
Points studied |
|
1 |
Probability,Event,Favourable event, exclusive Event |