1.4 Irrational numbers:

 

Every rational number can be expressed as a decimal number.

For example 1/2 = 0.5, 1/4= 0.25, 1/8 = 0.125, 1/5 = 0.2 and so on.

These rational numbers have fixed number of digits after the decimal point.

These are rational numbers whose reminder becomes zero after few successive divisions (division is exact).

However, there are rational numbers like 1/3 and 1/7 where the reminder does not become zero even after several successive divisions.

Moreover, we notice that 1/3 = 0.33333 ..  And 1/7 = 0.142857142857142857….

The recurring part of non-terminating recurring decimal is called the ‘period’ and the number of digits in the recurring part is called ‘periodicity’

1/3 is also represented as 0. (Implying (meaning) that the digit 3 repeats itself. In this case 3 is the period and periodicity is 1)

1/7 is also represented as 0. (Implying that the group 142857 repeats itself. In this case 142857 is the period and periodicity is 6)

In the case of 1/4, the decimal has only 2 digits after the decimal point and they are called terminating decimals. Where as in the case of 1/3 and 1/7 there is no fixed number of digits after the decimal point and the group of digits repeat themselves. Such decimals are called non terminating and recurring decimals.

Terminating decimals and recurring decimals can be expressed as rational numbers which is of the form p/q with q 0.

But, non terminating and non recurring decimals cannot be expressed in the form p/q with q 0.

 

Definition:  Non terminating and non recurring decimals/numbers which cannot be written in the form p/q with q 0 are called irrational numbers.

Examples are  =1.41421356237310 and = 2.23606797749979

In Sulabhasutras which dates back to Vedic period, value of    is given as = 1 +1/+{(1/4)*(1/3)} – {(1/34)*(1/4)*(1/3)} = 1.41421356

Another irrational number is   whose approximate value = 3.14159265358979

 

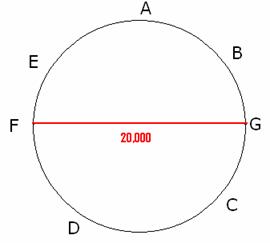
Aryabhatta the Indian mathematician of 5th century AD was the first one to give approximate value of  to 4 correct decimal places (3.1416).

 

His formula is :

 

The approximate circumference of a circle of diameter 20000 units is got by adding 62000 to the result of 8 times the sum of 100 and 4.

 

Circumference = 62000+ 8(100+4) = 62832;

diameter = 200

 

= circumference ÷ diameter = 62832 ÷ 20000= 3.1416

 

 

Note: Since   is an irrational number, 4+ is also an irrational number and hence  is also an irrational number.

The square roots and cube roots of natural numbers whose exact value cannot be obtained are irrational numbers (Ex:, and also 5,8)

 

 

 

1.4 Summary of learning

 

 

No

Points studied

1

Irrational numbers

 

 

Additional Points:

 

 

1.4 Problem 1: Show that 0.477777 is a rational number

We need to show that the given number is of the form p/q

 

Solution:

Let x = 0.4. Note that only one digit, 7 (periodicity = 1) repeats, so we multiply both sides by 10.

(As a general rule we multiply both sides by 10n, where n is the ‘periodicity’ (number of digits that repeat): If 3 digits repeat, multiply both sides by 103)

10x = 4.77777…. = 4.3+0.47777… = 4.3+x

9x = 4.3 = 43/10

x = 43/90

Verify that 43/90 = 0.47777

Thus, a number whose decimal expansion is terminating or non-terminating and recurring is rational.

 

Observations:

1.  The sum or difference of a rational number and an irrational number is irrational (4 + )

2.  The product or quotient of a non-zero rational number with an irrational number is irrational ( 2, (1/2)*)

3.  Addition/subtraction/multiplication/division of irrational numbers may be rational or irrational

( -= 0 is rational,+ =2 is irrational, * = 5 is rational, * =  is irrational, ÷ = 1 is rational, ÷ =  is irrational )