1.7 Surds:

We have learnt to locate rational numbers on the number line. Is it possible to locate any irrational number on a number line?

By using calculator we find that the value of  =1.41421356237310. . .and = 2.23606797749979. . . .

The numbers such as,, , are not rational numbers. They have non recurring and non terminating decimal points. They are called surds.

A ‘surd’ is defined as an irrational root of a rational number and is of the form

with a >0 and n>1.

‘a’ is called ‘radicand’ and ‘n’ is called ‘order’ . is the root sign.

We note that every surd is an irrational number but every irrational number need not be a surd (e.g. , are irrationals but not surds)

Surds can be expressed in exponential (index) forms as shown below.

= 2^1/2, = 5^1/3, 8= 8*7^1/5

Observations:

1. (2^1/2) *(2^1/2) = * = 2. We also know by first law of indices that (2^1/2) *(2^1/2) =2^1/2+1/2 = 2¹= 2

2. ()* ()*() = = 4 and by first law of indices 4^1/3*4^1/34^1/3 = 4^1/3+1/3+1/3= 4^3/3= 4¹=4

Some times surds can be reduced to its simplest form: For example:

=(405)^1/4 = (81*5)^1/4 = (3⁴*5)^1/4 = 3^4*1/4* 5^1/4 = 3¹*5^1/4= 3

Surds which have 1 as its rational co- efficient are called ‘pure surds’. The examples are, , .

Surds which have rational co-efficients other than 1 are called ‘mixed surds’. The examples are 5,8,4(Their co –efficients are 5, 8, 4 respectively).

Surds whose order and radicands are same in their simplest form are called ‘like surds’. The examples are 5,7.8 ( Their order is two and radicand is 3).

Surds whose order or/and radicands are not the same in their simplest form are called ‘unlike surds’. The examples are

(i) , , ( Though the order is 2, radicands are different)

(ii), , , , 4 ( Though the radicand is 4, orders are different)

From law of indices (Refer section 2.2), and ordering of real numbers, we have following laws on surds

1. ()ⁿ =a

2. * =

3. / =

4. If =then a=b

5. If >then a>b

6. If <then a<b

1.7 Problem 1 : Compare and

Solution:

Since the order of two surds(3 and 4) are different we need to convert their orders in to same number. The smallest common order is the LCM of 3 and 4 which is 12.

= 4^1/3= 4^4/12 = (4⁴)^1/12=256^1/12=

=6^1/4 = 6^3/12= (6³)^1/12=216^1/12=

Since 256>216 it follows that >

I.e. >

Note : For most of operation on surds, it is necessary that they are converted first to same orders.

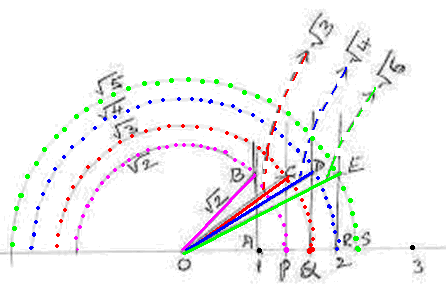
1.7.1 Representing square root of numbers on number line:

We have learnt to represent integers and fractions on a number line.

We have also studied earlier that by division method (Section 1.5.2), we can find the value of to the required number of decimal places.

to 5 decimal places is =1.73205

With non repeating and non terminating decimal value of, we can not accurately represent on a number line.

But, with the help of Pythagoras theorem we can represent irrational number of the form on a number line accurately.

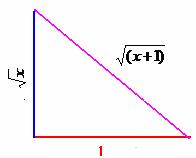
Note that any number x, can be represented as

()² = x +1 = ()²+1² ====è(1)

We know that in a right angled triangle, square of hypotenuse is equal to sum of squares of other two sides (Proof given in 6.11)

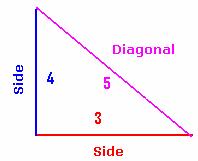
(Hypotenuse)² =(1^st Side)² +(2^nd Side)²

1^st Side	2^nd Side	Equation	Hypotenuse
4	3	5^2= 25 = 16 + 9 = 4^2+3^2	5
12	5	13^2= 169 = 144+ 25 = 12^2+5^2	13
20	15	25^2= 625 = 400+225 = 20^2+15^2	25

By observing equation (1), we can conclude that if the sides of a right angled triangle are 1 and then the hypotenuse of that triangle =

Sides of right angled triangle =	Pythagoras theorem	Hypotenuse=
1, 1	1^2+ 1^2=()^2
, 1	()^2+ 1^2=3^2
,1	()^2+ 1^2=4^2
………	…….	……
,1	()^2+ 1^2=(99)^2
In general ,1	()^2+ 1^2=(x+1)^2

Thus, if we can construct a right angled triangle whose sides are, 1 (say base of and height of 1), then the hypotenuse gives the value of.

Let us find values of,

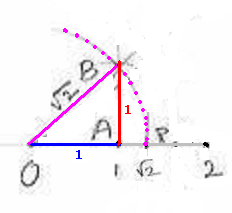
1.7.1 Problem 1: Locate on number line

Draw a number line and mark O. Mark the point A, say at a distance of 1cm from O. Therefore OA=1cm. At A, draw a perpendicular to the number line. Draw an arc of 1cm from A to cut this perpendicular line at B. Join AB. Therefore AB=1cm.Join OB Thus, we have a right angled triangle OAB whose sides OA = AB = 1cm. By Pythagoras Theorem OB^2=OA^2+AB^2 = 1^2+1^2= 1+1 =2 OB= With OB as radius, draw an arc to cut the number line at P. OP =

1.7.1 Problem 2: Locate on the number line.

Solution:

At P draw a perpendicular line to the number line. With P as center and 1cm as radius draw an arc to cut this perpendicular line at C. Join PC Therefore PC=1cm. Join OC By Pythagoras Theorem OC^2=OP^2+PC^2 = ()^2+1^2 =2+1 OC= With OC as radius draw an arc to cut the number line at Q. OQ=

Observe the adjacent figure:

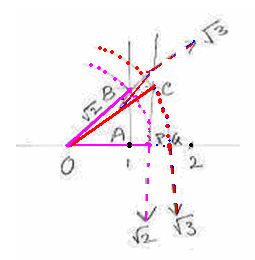
We note that with O as center, we have concentric circles whose radii (OB,OC,OD,OE….) are,,, respectively… In the same way we can locate for any positive integer n after has been located. This is called Wheel of Theodorus named after a Greece philosopher, Theodorus. Every number (rational or irrational) is represented by a unique point on the number line(refer later part of this section) Also, every point on the number line represents a unique real number.

1.7 Summary of learning

No	Points studied
1	Surds, laws on surds, Locating irrational numbers on number line

Additional points:

Representing real numbers on the number line:

We have learnt how to represent rational numbers on the number line in 1.1 and how to represent on the number line in this section.

We have also learnt that every irrational number has a decimal representation.

Thus, if we could represent a decimal number on the number line, then we can conclude that every irrational number can also be represented on the number line.

1.7.1 Problem 2: Locate 3.1415 on the number line.

Solution:

We know that the given number 3.1415 lies in between 3 and 4.

Draw a number line with a large scale.

Identify 3 and 4 on this line. Divide the portion between 3 and 4 into 10 equal parts.

Identify 3.1 and 3.2 on this line. Again divide the portion between 3.1 and 3.2 into 10 equal parts.

Identify 3.14 and 3.15 on this line. Again divide the portion between 3.14 and 3.15 into 10 equal parts.

Identify 3.141 and 3.142 on this line. Again divide the portion between 3.141 and 3.142 into 10 equal parts.

Identify 3.1415 on this line.

Thus we have located on the number line to an approximate value of 3.1415.

In this way we conclude that any irrational number can be represented on the number line.

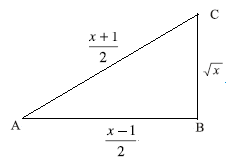
1.7.1 Problem 3: Locating when x is any positive number (rational or irrational) on the number line.

Solution:

We know that any real number can be represented in decimal form. Let x be the given number and we know how to represent this on the number line (Refer 1.7.1 Problem 2) Similarly, we can represent (x+1)/2 and (x-1)/2 on the number line, as they are also real numbers. Then Construct a right angled triangle with base (AB) = (x-1)/2 and hypotenuse (AC) = (x+1)/2. By Pythagoras theorem we know that AC^2= AB^2+BC^2 i.e. BC^2= AC^2-AB^2 = {(x+1)/2}^2-{(x-1)/2}^2 = {(x+1)^2-(x-1)^2}/4 = 4x/4 =x BC = With BC as the length, we can draw an arc from 0 to cut the number line which then represents

Addition/Subtraction of Like Surds:

1.7.1 Problem 3: Simplify +-

Solution:

Since 50 =25*2 = 5²*2

= 5

Since 32 =16*2 = 4²*2

= 4

Since 72 =36*2 = 6²*2

= 6

+- = 5+4-6 =(5+4-6) = 3

For multiplication and division of surds having same order follow the following rule: (Refer 1.7 Problem 1)

* = and / =

Note: If orders are different then find LCM of orders to convert them to same order.

Rationalization:

The process of multiplication of two irrational numbers to get their product as a rational number is called ‘rationalisation’.

The two irrational numbers are called rationalising factors of each other.

We have seen earlier that is an irrational number. What about the product of and 3?

*3 = 3*2 = 6 which is a rational number.

Thus 3 is a rationalising factor of. Similarly is also a rationalising factor of .

Also note that 1/ is also a rationalizing factor of .

Thus rationalising factor is not unique. In fact the product of a rational number and the rationalising factor is also a rationalising factor.

1.7.1 Problem 3: Rationalize the denominator in 1/(-2)

Solution:

We are required to convert the denominator into a rational number.

Let us multiply the numerator and the denominator by (+2)

1/(-2) =(+2)÷ {(-2)*(+2)}

By expanding the terms in the denominator or by using an identity (a+b)*(a-b) = a²-b² (refer to section 2.3)

We note that {(-2)*(+2)} = 7-4 =3

1/(-2) =(+2)/3

Thus 1/(+2) is the rationalising factor of the denominator.

If the product of two mixed surds a+and a-(where a and b are rational numbers) is a rational number then they are called conjugate surds and a+and a-are conjugate to each other.