2.8 Factorisation of algebraic expressions:

 

We have learnt how to factorise algebraic expressions similar to:

 

No

Expression

Factors

1

(p-q)2- 3(p-q)

(p-q){(p-q)-3}

2

2x(a-4b)+3y(a-4b)

(a-4b)(2x+3y)

3

m2(pq+r)+mn(pq+r)+ n2(pq+r)

(pq+r) (m2+mn+ n2)

 

Refer to section 2.5 to recall how we factorised the expression of type px2+mx +c.

 

2.8.1 Factorisation using identities/formulae:

 

We have learnt the following identities in section 2.3

 

No

Formula/Identity

Expansion

Factors

1

(a+b)2

a2+b2+2ab

(a+b) and (a+b)

2

(a-b)2

a2+b2-2ab

(a-b) and (a-b)

3

(a+b)(a-b)

a2-b2

(a+b) and (a-b)

4

(x+a)*(x+b)

x2+x(a+b)+ab

(x+a) and (x+b)

 

2.8.1 Problem 1 : Factorize 9p2+12pq +4q2 using  an identity

 

Solution:

The expression can be rewritten as 9p2 +4q2+12pq. This is of the form a2+b2+2ab with a2= 9p2 , b2=  4q2 and 2ab=12pq

 

However 9p2  can be split as 3p*3p =(3p)2 and 4q2 = 2q*2q= (2q)2and 12pq = 2*3p*2q

So we can say a=3p and b=2q

Since the given expression is of the form a2+b2+2ab we can say the factors are (a+b) and (a+b)

The factors are (3p+2q) and (3p+2q)

 

Verification:

(3p+2q)(3p+2q)

=3p(3p+2q)+2q(3p+2q) ( Multiply each  of the terms)

=9p2+6pq +6qp+4q2 (simplification)

= 9p2+12pq +4q2  which is the term given in the problem

 

2.8.1 Problem 2: Factorize 36x2-60x +25 using  an identity

 

Solution:

The expression can be rewritten as 36x2 +25-60x. This is of the form a2+b2-2ab with a2= 36x2, b2=  25=52 and -2ab=-60x

However 36x2  can be split as 6x*6x = (6x)2 and 25 =52 and -60x = -2*6x*5

So we can say a=6x and b=5.

Since the given expression is of the form a2+b2-2ab we can say the factors are (a-b) and (a-b).

The factors are (6x-5) and (6x-5).

 

Verification:

(6x-5) (6x-5)

=6x(6x-5)-5(6x-5) ( Multiply each  of the terms)

=36x2-30x -30x+25 (simplification)

= 36x2-60x +25 which is the term given in the problem.

 

2.8.1 Problem 3 : Factorize (x+2)2+18(x+2) +81 using  an identity

 

Solution:

The expression can be rewritten as (x+2)2 +81+18(x+2). This is of the form a2+b2+2ab with a2= (x+2)2 , b2= 81=92 and 2ab=18(x+2)

So we can say a=x+2 and b=9 and hence 2ab = 2(x+2)*9 =18(x+2)

Since the given expression is of the form a2+b2+2ab we can say the factors are (a+b) and (a+b)

The factors are ((x+2)+9) and ((x+2)+9)

 

Verification:

Verify yourself that ((x+2)+9)((x+2)+9)= (x+2)2+18(x+2) +81

 

2.8.1 Problem 4: Factorize p4/16- q2/64 using an identity

 

Solution:

The expression   is of the form a2-b2 with a2= p4/16= (p2/4)2 and  b2= q2/64 = (q/8)2

So we can say a=p2/4 and b=q/8.

Since the given expression is of the form a2-b2 we can say the factors are (a+b) and (a-b).

The factors are (p2/4+q/8) and (p2/4-q/8).

 

Verification:

(p2/4+q/8)(p2/4-q/8)

=p2/4(p2/4-q/8)+q/8(p2/4-q/8) ( Multiply each  of the terms)

=(p2/4)2-p2q/32 +qp2/32 –(q/8)2 (simplification)

= p4/16- q2/64  which is the term given in the problem

 

2.8.1 Problem 5: Factorize 8(x+1/x)2-18(x-1/x)2  using  an identity

 

Solution:

We notice that 8 and 18 are not squares of any number. But we observe 8 =2*4 and 18 =2*9. We also notice that 4 and 9 are squares of 2 and 3 respectively.

Therefore we can rewrite the expression 8(x+1/x)2-18(x-1/x)2 = 2{4(x+1/x)2-9(x-1/x)2}.

The expression  4(x+1/x)2-9(x-1/x)2  is of the form a2-b2 with a2= 4(x+1/x)2 =(2(x+1/x))2  and  b2=(3(x-1/x))2

So we can say a=2(x+1/x) and b=3(x-1/x)

Since the given expression is of the form a2-b2 we can say the factors are (a+b) and (a-b)

The factors of 4(x+1/x)2-9(x-1/x)2  are(2(x+1/x) + 3(x-1/x)) and (2(x+1/x) - 3(x-1/x))

Since we had taken 2 as common factor from the given expression,

The factors of 8(x+1/x)2-18(x-1/x)2  are  2 , (2(x+1/x) + 3(x-1/x)) and (2(x+1/x) - 3(x-1/x))

 

Verification:

Exercise : Verify yourself that 2(2(x+1/x) + 3(x-1/x))(2(x+1/x) - 3(x-1/x))= 8(x+1/x)2-18(x-1/x)2

 

2.8.1 Problem 5: If the difference of two numbers is 8 and the difference between their squares is 400, find the numbers ( Lilavati Shloka 59)

 

Solution:

Let the numbers be x and y, then

x2 -y2 =400

x-y= 8  ( x= y+8)   ------(1)

 

x2 -y2  = (x+y)*(x –y)  {a2-b2 =(a+b)*(a-b)}

         = 8(x+y)           ( x-y =8)

 400 = 8(x+y)          ( x2 -y2 =400)

 (x+y) = 50             (Division by  8 )

 

  y+8+y =50            (Substitute from  (1)

  2y = 42                (By simplification)

  y =21

  x=  29                  ( Substitute in (1)

Verification:

29-21 =8

292-212 = ??

 

2.8.2 Product of three binomials

We have learnt that

(x+a)*(x+b) = x2+x(a+b)+ab

Using this identity let us find product of (x+a)*(x+b)*(x+c)`

(x+a)*(x+b)*(x+c)

= {(x+a)*(x+b)}*(x+c)

= {x2+x(a+b)+ab}*(x+c)

= x2(x+c)+x(a+b)*(x+c) + ab(x+c) ( every term of {x2+x(a+b)+ab} is multiplied with  the every other term of (x+c)

= x3+ x2c + x(a+b)*x+x(a+b)*c + abx+abc ( every term of x(a+b) is multiplied with  the every other  term of (x+c) )

= x3+ x2c + x2(a+b)+x(a+b)*c + abx+abc (expansion)

= x3+ x2(c+a+b)+xac+xbc + abx+abc (expansion and simplification)

= x3+ x2(a+b+c)+x(ac+bc+ ab)+abc (simplification)

= x3+ (a+b+c) x2+(ab+bc+ca)x+abc (Rearrangement)

 

Let us put b=a and c=a in the identity (x+a)*(x+b)*(x+c)` then we get

(x+a)(x+a)(x+a)

= x3+ (a+a+a) x2+(a*a+a*a+a*a)x+a*a*a

= x3+ 3ax2+3a2x+ a3

= x3+ 3ax(x+a)+ a3

(x+a)3 = x3+ 3ax(x+a)+ a3

If we replace x by a and a by b we get the formula/identity

(a+b)3 = a3+ 3ab(a+b)+ b3

If we substitute –b for b in the above formula we get

(a-b)3

= a3+ 3a*-b(a-b)+ (-b)3

= a3-3ab(a-b)-b3

 

2.8.2 Problem 1: Find the value of 1.05*0.97*.98

 

Solution:

1.05 = 1+.05, 0.97 = 1-0.03 and 0.98 = 1-0.02 and they can be represented as x=1 and a=.05, b=-0.03 and c= -0.02

Therefore the given product can be expressed as (x+a)(x+b)(x+c)

We know (x+a)(x+b)(x+c)

= x3+ (a+b+c) x2+(ab+bc+ca)x+abc, By substituting values for x, a, b , c we get

1.05*0.97*.98

= 13+ (0.05-0.03-0.02) 12 +((0.05*-0.03) (–0.03* -0.02)(-0.02*0.05))1+ 0.05*-0.03*-0.02

= 1+ 0 12+(-0.0015+0.0006-0.0010)1+ 0.000030

= 1- 0.0019+0.00003 =0.998130

 

Verification:

Verify using calculator that 1.05*0.97*0.98 = 0.998130.

 

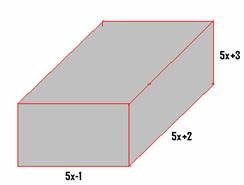
2.8.2 Problem 2 : Find the volume  of a cuboid whose sides are (5x+2)cms, (5x-1)cms, (5x+3)cms

 

Solution:

We know the volume of cuboid = length*breadth*depth.

 

So the given cuboid’s volume=(5x+2)(5x-1)(5x+3)cc.

The product is of the form (x+a)(x+b)(x+c)  with x=5x and a=2, b=-1 and c=3

Therefore the given product can be expressed as (x+a)(x+b)(x+c)

We know  (x+a)(x+b)(x+c)= x3+ (a+b+c) x2+(ab+bc+ca)x+abc,

= (5x)3+ (2-1+3) (5x)2+(-2-3+6)(5x)+ 2*-1*3(By substituting values for x, a, b , c)

= 125x3+ 100x2+5x-6

 

 

Verification: (for one value of x)

Let the value of x in the sides of cuboid be 2

Hence the sides are:

1.5x+2=5*2+2=12.

2.5x-1 =5*2-1=9

3.5x+3 =5*2+3= 13

From the solution arrived above the volume of the cuboid

= 125x3+ 100x2+5x- 6 = 125*8+100*4+5*2-6

= 1000+400+10-6=1404 (As arrived from the formula)

However, we know the volume of cuboid whose sides are12,9 and 13 is

=12*9*13 = 1404 cubic units.

Since the volume arrived from two different methods are same our solution is correct.

 

We have seen that (x+a)(x+b)(x+c)= x3+ (a+b+c) x2+(ab+bc+ca)x+abc and we observe

1. The co-efficient of x2 in (a+b+c) x2 is (a+b+c)

2. The co-efficient of x in (ab+bc+ca)x is (ab+bc+ca)

 

2.8.2 Problem 3: Find the co-efficient of  x2 and x in (3x-1)(3x-1)(3x+4)

 

Solution:

The product is of the form (x+a)(x+b)(x+c)  with x=3x and a=-1, b=-1 and c=4

Therefore the given product can be expressed as (x+a)(x+b)(x+c)

We know (x+a)(x+b)(x+c)= x3+ (a+b+c) x2+(ab+bc+ca)x+abc.

= (3x)3+(a+b+c)(3x)2 + (ab+bc+ca)(3x)+abc (By substituting 3x for x)

 

1. The co-efficient of x2 in (a+b+c) (3x)2 is (a+b+c)*9.  By substituting  values for a,b and c we get:

The co-efficient of x2 is (a+b+c)*9 = (-1-1+4)*9 = 18

 

2. The co-efficient of x in (ab+bc+ca)(3x) is (ab+bc+ca)*3. By substituting values for a,b and c we get:

The co-efficient of x in (ab+bc+ca)3x is (ab+bc+ca)*3 = (1-4-4)*3 = -21

 

Verification:

Expand (3x-1)(3x-1)(3x+4) and check the co-efficients

 

We have seen earlier that

(a+b)3 = a3+ 3ab(a+b)+ b3

 (a+b)3 -3ab(a+b) = a3+ b3(By transposition)

i,e a3+ b3

=(a+b)3 -3ab(a+b)

= (a+b){ (a+b)2 -3ab}

= (a+b) { a2 +b2 +2ab -3ab}(By expanding (a+b)2)

= (a+b) (a2 +b2  -ab)

By Substituting –b for b in the above identity we get

a3+ (-b)3

= (a+-b) (a2 +(-b)2  -a*(-b))

= (a-b) (a2 +b2 +ab)

But a3+ (-b)3= a3-b3

 a3-b3= (a-b) (a2 +b2 +ab)

 

2.8.2 Problem 3: Factorise 0.027 p3+0.008 q3

 

Solution:

Note 0.3*0.3*0.3=0.027 and 0.2*0.2*0.2=0.008

Therefore the given expression is of the form a3+b3 with a=0.3p and b= 0.2q

By using a3+b3=(a+b) (a2 +b2 -ab)  and substituting for a and b we get

0.027 p3+0.008 q3

= (0.3p+0.2q) ((0.3p)2 +(0.2q)2 -0.3p*0.2q)

= (0.3p+0.2q) (0.09p2 +0.04q2 -0.06pq)

 

Verification: (for one value of p and q)

Let p=1 and q=1, By substituting these in  the solution we get

(0.3p+0.2q) (0.09p2 +0.04q2 -0.06pq)

= 0.5*(0.09+0.04-0.06) = 0.5*0.07 = 0.035

Also

0.027 p3+0.008 q3 =0.027+0.008 =0.035

Since the results got by both methods are same, our solution is correct

 

2.8.2 Problem 4: Factorise 125 -1/ a3b3

 

Solution:

Note that 125 = 53 and 1/ a3b3=(1/ ab)3

Therefore the given expression is of the form a3-b3 with  a=5  and b= 1/ab

By using a3-b3=(a-b) (a2 +b2 +ab)  and substituting for a and b we get

125 -1/ a3b3

= (5 -1/ab) (52 +(1/ab)2 +5*1/ab)

= (5 -1/ab) (25 +1/a2 b2 +5/ab)

 

Verification: (for one value of a and b)

Let a=1 and b=2, By substituting these in the solution

(5 -1/ab) (25 +1/a2 b2 +5/ab)

=(5-1/2)(25+1/4+5/2) =124.875(Use calculator)

Also

125 -1/ a3b3

= 125-1/8= 124.875(Use calculator)

Since the results got by both methods are same our solution is correct

 

 

2.8 Summary of learning

 

 

No

Formula/Identity

Expansion

Factors

1

(a+b)2

a2+b2+2ab

(a+b) and (a+b)

2

(a-b)2

a2+b2-2ab

(a-b) and (a-b)

3

(a+b)(a-b)

a2-b2

(a+b) and (a-b)

4

(x+a)*(x+b)

x2+x(a+b)+ab

(x+a) and (x+b)

5

(x+a)(x+b)(x+c)

x3+ (a+b+c)x2+(ab+bc+ca)x+abc

(x+a),(x+b)and (x+c)

6

(a+b)3

a3+b3+3ab(a+b)

(a+b),(a+b) and(a+b)

7

(a-b)3

a3-b3-3ab(a-b)

(a-b),(a-b) and(a-b)

8

a3+b3

(a+b) (a2 +b2 -ab)

(a+b) and (a2 +b2 -ab)

9

a3-b3

 (a-b) (a2 +b2 +ab)

(a-b) and (a2 +b2 +ab)