3.1 Introduction to Sets:
A class has 60
students. Every one should choose to be in Kabadi team or hockey team or in
both the teams. If 45 students chose to be in Kabadi team and 30 students chose to be in Hockey
team, how many are in both the teams?
Can you answer
the above question quickly? We find answer to this question in the topic 3.3.
Study of sets
helps us to solve problems similar to the given above
Definition: A
‘set’ is a collection of well defined
objects. The objects which are members of the set are called elements. The elements of a set are listed within
{ }
A = {1, 4, 9, 16…}
B= {1, 8, 27, 64…}
A set can be represented
either by listing elements or by the rule.
The above set A can also be
represented as
C = {Perfect square
numbers}
D = {Perfect cube numbers}
The method by which we list
the individual elements of the set is called ‘roster
method’ as is the case with sets A and B
The method by which we
describe the set by specifying the common property of the elements of set is
called ‘rule method’ as is the case with
sets C and D.
Notes:
1. Definition of the set
should be such that the objects are easily identifiable. With the clear
definition, it should be possible to conclude whether an object belongs to the
set or not. ‘Collection of tall people’ can not be a set; because the
subjective word ‘tall’ can not identify people. However group of people whose
height is more than 175cm is a set.C = {set of people whose height
>175cm}.With this definition, we can clearly say whether a person belongs to
the set or not.
2. Listing of elements in a
set in an orderly or logical manner is not important.
For example, E = {1, 4, 9,
16…} is same as {4, 9, 16, 1, ..}.
3. An element need not be
listed more than once even if the element is repeated.
For example, F ={1,2,3,4 } is same as {1,2,3,3,4}
Let X = {x: x is an odd number such that 2<x<10}
The odd numbers are 1, 3,5,7,11,13….
Since the definition of X
is such that the odd number has to be < 10 and > 2
X = {3, 5, 7}.
We note that 3 is an
element of set X (We say that 3 belongs to X and
symbolically this is denoted by 3 ![]() X.).
X.).
Though 11 is an odd number
it is not an element of X (We say that 11 does not belong to X and symbolically
this is denoted by 11![]() X).
X).
Are 1900 and 2000 leap
years?
Since 1900 is divisible by
4 and also divisible by 100, 1900 is not a leap year.
Since 2000 is divisible by
4 and it is also divisible by 400, 2000 is a leap year
Hence, 1900 ![]() {Leap Years} and 2000
{Leap Years} and 2000 ![]() {Leap years}
{Leap years}
Have you noticed that, we
can not count the number of elements in the set E?
However in case of set X,
we could count the number of elements which is = 3
Definition: A
finite set is a set which has countable
number of elements. An
infinite set is a set whose elements are not countable
(They have infinite number of elements).
Can a set have no elements
(Zero number of elements) ?
Observe
Y = {number of human beings
on moon}
Z = {z :
z is a prime number between 8 and 10}
These two sets do not have
any element at all.
Definition:
A set which has no elements is called an empty set
or null set.
Null set is denoted by { }
or ![]() (pronounced as ‘phi’).
(pronounced as ‘phi’).
Note that {0} is not a null
set as it has one element 0 in it.
|
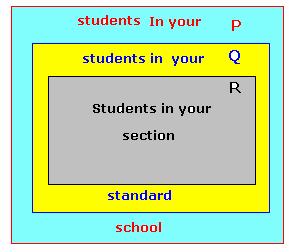
Let us
consider the following examples P =
{Students of your school} Q =
{Students of your
standard} R = {Students of your section} Is there
a relation ship between these three sets? 1.
‘Students of your section’ are also ‘Students of your standard’ and ‘Students
of your standard’ are also ‘Students of your school’, 2. Set
P has more elements than the number of elements in Q and set Q has more
elements than R. In
simple terms, P is bigger than Q and Q is bigger than R. Mathematically
we say that R is a sub set of Q and Q is a sub set of P and their
relationship is symbolically represented as R
The
parent set P is called a universal set
of Q and R. |
|
Definition
: If A and
B are two sets such that every element of B is also an element of A, then we
say, B is a ‘sub set’ of A. Their
relationship is written as B ![]() A.
A.
Definition
: The main or the bigger
set from which elements are taken out to
form subsets is called the ‘universal set’ and
is denoted by U.
Note that the universal set
contains all the elements of all the sub sets under consideration. All sub sets
are derived from universal set.
Let X= {1,3,5,7}
Does {3,5,7,1} ![]() X ? Yes it is
X ? Yes it is
What about the null
set? Since null set does not have any
element, it is a subset of every set.
Every set is
a sub set of itself. Every set ![]() itself
itself
An empty set
is a sub set of every set. ![]()
![]() every
set
every
set
Definition: A set having a single
element is called a ‘singleton set’
P = {Set of even prime
numbers}, X = {Identity element of
addition}, Y= {1} are all examples of singleton sets.
Let Q = ![]()
Then ![]() is a sub set of Q (When
a set has no elements, we have 1 sub set)
is a sub set of Q (When
a set has no elements, we have 1 sub set)
Let P = {p, q)
Then P0 =![]() , P1 = {p}, P2 = {q} and P = {p,
q) are all the subsets of P (When a set has 2 elements we have 4 sub sets)
, P1 = {p}, P2 = {q} and P = {p,
q) are all the subsets of P (When a set has 2 elements we have 4 sub sets)
Let A = {a, b, c}
A0 =![]() , A1 = {a}, A2 = {b} A3
={C}, A4 = {a, b}, A5 = {b, c}, A6 ={c, a} and
A = {a, b, c} are all the subsets of A. (When a set has 3 elements we have 6
sub sets)
, A1 = {a}, A2 = {b} A3
={C}, A4 = {a, b}, A5 = {b, c}, A6 ={c, a} and
A = {a, b, c} are all the subsets of A. (When a set has 3 elements we have 6
sub sets)
|
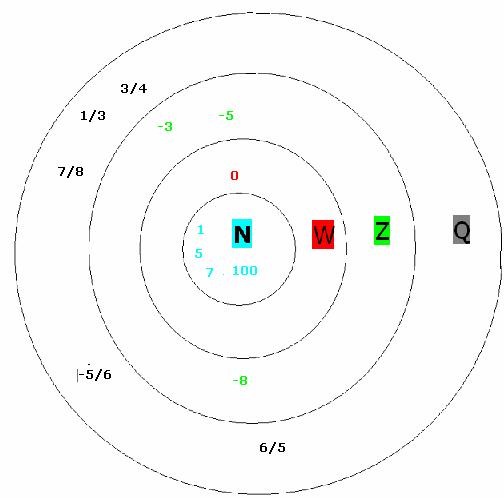
In
topic 1.1 we have studied different type of numbers and let us try to
represent them using set notations. If N = {Set
of natural numbers}, W={Set of
whole Numbers}, Z= {Set
of integers} and Q= {set of rational numbers} Then N Note
All these are infinite sets. |
|
3.1
Summary of learning
|
No |
Points
learnt |
|
1 |
Definitions
of Finite set, Infinite set, Elements, Null set, Sub set, Universal set |