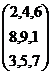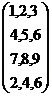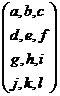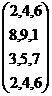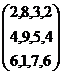3.5 Types of Matrices:
Definitions:
|
‘Square Matrix’ is a matrix whose number of rows are same as number of columns.
Square matrix’s order is represented by m (m x m) |
||
|
A= B= |
The
Principal diagonal elements (from top left corner to bottom right corner) of
matrix A are {1,5,9} The
Principal diagonal elements (from top left corner to bottom right corner) of
matrix A are {1,4} |
|
|
A= B= |
Note
Matrix A is 3X2 and Matrix B is 2X3 Since
these two are not square matrices, we cannot identify their diagonal
elements. |
|
|
A matrix whose principal diagonal
elements are non zero and all other elements are zero is called ‘Diagonal matrix.’ |
||
|
A= B= |
Observe
that in both A and B except for diagonal elements all other elements are
zero. |
|
|
A ‘Scalar matrix’ is a diagonal matrix whose principal
diagonal elements are equal |
||
|
A= B= |
|
|
|
An ‘Identity matrix’ is a diagonal matrix
whose principal diagonal elements are 1. |
||
|
A= B= |
|
|
|
‘Symmetric matrix’ is a square matrix whose elements are symmetric (same) with respect
to principal diagonal elements. (Mirror
copy with respect to principal diagonal). |
||
|
A= B= |
Notice
that in A the elements on both the sides of principal diagonal are same {-2,-2},{-4,-4},{6,6}. Notice
that in B the elements on both the sides of principal diagonal are same {-2,-2}. |
|
|
Skew symmetric matrix’ is a square matrix whose elements are symmetric with respect to the
principal diagonal with opposite sign and principal diagonal elements are
zero |
||
|
A= B= |
Notice
that in A the elements on both the sides of principal diagonal are same with
opposite sign {-2,2},{4,-4},{-6,6}.) Notice
that in B the elements on both the sides of principal diagonal are same with
opposite sign {-2,2}.) |
|
|
A= B= |
Row matrix’ is a matrix which has only one row and is of the order (1 x n) |
|
|
A= B= |
‘Column matrix’ is a
matrix which has only one column and is of order (m x 1) |
|
|
A= B= |
‘Zero matrix’ is a matrix whose elements are all zeros. It need
not be a square matrix |
|
|
A= B= |
Two
matrices are said to be ‘equal’ if and only if they are of same order and
corresponding elements are equal. |
|
A= B = |
a=1,
b=2,c=3,d=4,e=5,f=6,g=7,h=8,i=9,j=2,k=4,l=6.
Rows Columns |
|
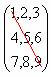
‘Transpose of a matrix’ is obtained by converting elements of rows
in to columns and elements of columns in to rows. Transpose of A is denoted by A1. |
|
|
A= A1= |
Rows: {2,4,6},{8,9,1},{3,5,7},{2,4,6}. Columns: {2,8,3,2},{4,9,5,4},{6,1,7,6} Rows: {2,8,3,2},{4,9,5,4},{6,1,7,6}. Columns: {2,4,6},{8,9,1},{3,5,7},{2,4,6} |
3.5
Summary of learning
|
No |
Points
studied |
|
1 2 |
Types of matrices - Square matrix, rectangular
matrix, diagonal matrix, Symmetric matrix, Zero matrix, Skew matrix, Identity
matrix Transpose of a matrix |
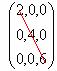
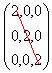
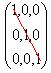
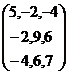 Principal diagonal elements are {5, 9,6}
Principal diagonal elements are {5, 9,6}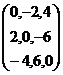 Principal diagonal elements are {0,0,0}
Principal diagonal elements are {0,0,0}