6.7 Quadrilateral:
6.7.1 Properties of Quadrilaterals ![]()
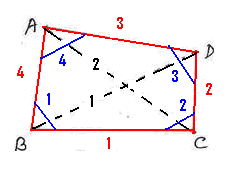
Definition: A ‘quadrilateral’
is a geometric figure on a plane enclosed by 4 line segments.
|
Properties:
Each diagonal divides the quadrilateral
in to 2 triangles
(
|
|
|
Adjacent Sides ( Have common vertex) |
Opposite Sides ( Do not have common
vertex) |
Adjacent Angles ( Have common
side) |
Opposite Angles ( Do not have
common side) |
|
(AB,BC) : B common vertex (BC,CD) : C common vertex (CD,DA) : D common vertex (DA,AB) : A common vertex |
(AB,CD) (AD,BC) |
( ( ( ( |
( ( |
We notice that the sum of all four interior
angles in a quadrilateral is 3600. Can we prove this mathematically?
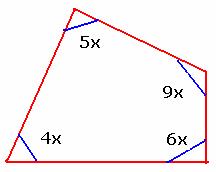
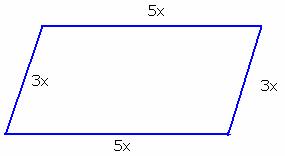
6.7.1 Problem 1:.The four angles of a quadrilateral are in the
ratio of 4:5:6:9. Find all the angles.
Solution:
|
The sum of all angles in a quadrilateral
is 3600. Since the angles are in the
ratio of 4:5:6:9, let they be 4x, 5x, 6x and 9x.
i.e. 24x = 3600 x = 360/24 = 150 4x = 4*15 = 600 5x = 5*15 =750 6x = 6*15 =900 9x= 9*15 = 1350 The angles are 600, 750, 900 and 1350 |
|
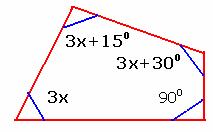
6.7.1 Problem 2: If the angles of a quadrilateral are 3x, 3x+150, 3x+300 and 900.Find all the angles.
Solution:
|
We know that sum of interior angles of a quadrilateral
is 360o
i.e.9x=2250 i.e. x=250 Therefore the angles are 3x = 750,
3x+150 =750+150=900, 3x+300
= 1050 Verify that the sum of these
four angles = 3600 |
|
We have seen earlier that a triangle totally has
six elements (3 sides and 3 angles). We have also learnt to construct triangles
with just three elements given (3 sides, 1 side
and 2 angles, 2 sides
and 1 included angle).
Note: With just three angles we cannot construct a unique
triangle.
Compared to a triangle, quadrilateral has 10 elements
(4 sides, 4 angles, 2 diagonals). We cannot draw a quadrilateral uniquely with
4 elements. We need at least 5 elements to draw unique quadrilaterals. However,
it will not be possible to construct a unique quadrilateral with 1 side and 4
angles.
We need any one group of the following set of
elements, to construct a unique quadrilateral.
6.7.1 Table 1:
|
No |
Given no. of Sides |
Given no.
of Diagonals |
Given no. of Angles |
No.
of elements required
|
|
1 |
2 |
2 |
1 |
5 |
|
2 |
2 |
1 |
2 |
5 |
|
3 |
4 |
1 |
- |
5 |
|
4 |
4 |
- |
1 |
5 |
|
5 |
3 |
- |
2(Included) |
5 |
|
6 |
3 |
2 |
- |
5 |
|
7 |
2(adjacent) |
- |
3 |
5 |
General
method for construction of quadrilateral:
(The method is more or less the same for
construction of quadrilateral, for any combinations of the data given in the above
table)
Notes:
a) Step for drawing a side:
First draw a line. Mark a point on this line
From the above point, draw an arc of given radius (length
of the side) to cut this line to get the required side.
b) Use protractor to construct angles of required
measure, wherever required.
c) For drawing of any figure follow the procedure:
Step 1: Draw a rough diagram
Step 2: Follow the steps described above (a,b), to construct
sides/angles of required measure.
1. When
two sides, two diagonals and one angle are given
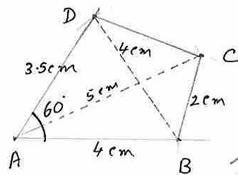
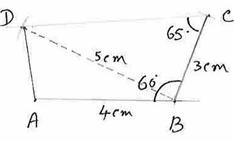
6.7.1 Problem 3: Construct a quadrilateral ABCD with AB=4cm, BC=2cm,
AC=5cm and BD=4cm and ![]() DAB= 600
DAB= 600
First draw a rough diagram
|
Step |
Construction |
|
|
1 |
Mark a point A and
draw a line though A |
|
|
2 |
With A as center, draw an arc of
radius 4cm to cut above line at B (AB=4cm) |
|
|
3 |
From B, dawn an arc of radius
2cm above AB |
|
|
4 |
From A, draw an arc of radius
5cm to cut the above arc at C (AC=5cm,BC=2cm) |
|
|
5 |
From A, draw a line at an angle
600 with AB |
|
|
6 |
From B, draw an arc of radius
4cm to cut the above line at D ( |
ABCD is the required quadrilateral.
2. When
two sides, one diagonal and two angles are given
6.7.1 Problem 4: Construct a quadrilateral ABCD
with AB=4cm, BC=3cm, BD=5cm and ![]() ABC= 600,
ABC= 600, ![]() BCD= 650
BCD= 650
First draw a rough diagram.
|
|
Construction |
|
|
1 |
Mark a
point A and draw a line though A |
|
|
2 |
Cut
the above line by an arc of radius 4cm to cut at B (AB=4cm) |
|
|
3 |
From
B, draw a line at an angle 600 with AB |
|
|
4 |
From B,
dawn an arc of radius 3cm to cut the above line at C (BC=3cm, |
|
|
5 |
From C,
draw a line at an angle 650 with AB |
|
|
6 |
From B,
draw an arc of radius 5cm to cut the above line at D (BD=5cm) |
ABCD is the required quadrilateral
3. When
four sides and one angle are given
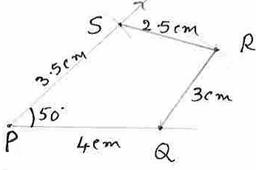
6.7.1 Problem 5: Construct a quadrilateral PQRS with PQ=4cm, QR=3cm,
RS=2.5cm and PS=3.5cm and ![]() SPQ= 500
SPQ= 500
First draw a rough diagram
|
Step
|
Construction |
|
|
1 |
Mark a
point P and draw a line though P |
|
|
2 |
Cut
the above line by an arc of radius 4cm to cut at Q (PQ=4cm) |
|
|
3 |
From P,
draw a line at an angle 500
with PQ |
|
|
4 |
From P,
dawn an arc of radius 3.5cm to cut the above line at S(PS=3.5cm, |
|
|
5 |
From S,
dawn an arc of radius 2.5cm. |
|
|
6 |
From Q,
dawn an arc of radius 3cm to cut the above arc at R(SR=2.5cm,QR=3cm). Join SR
and QR. |
PQRS is the required quadrilateral
6.7. 1 Exercise: In Table 6.7.1
we have listed seven combinations of
data required for construction of a quadrilateral, out of this we constructed
quadrilateral of three combinations (green color). Construct quadrilaterals with the four remaining
combinations of data (yellow
color).
6.7.2 Area of a Triangle
|
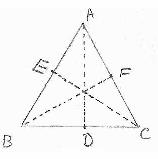
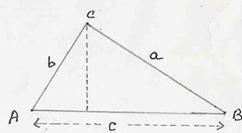
In the adjacent figure of
triangle ABC, AD, BF, CE are altitudes to the bases BC, AC and AB
respectively from the opposite vertices A,B and C respectively. Area of a triangle
=(1/2)Base*height(altitude) Area of We are going to
prove this formula for calculation of area of triangle in section 6.8.7. |
|
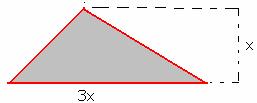
6.7.2 Problem 1: The base of a triangular field is three times its
height. If the cost of cultivating field at the rate Rs36.72 per 100 sq mts is
Rs 49,572, find its base and height
Solution:
|
Total cost of cultivating the
field = 49,572 Area of the fileld =
49572*100/36.72 = 135000 Let x be the height of the field
Thus height of the triangle is
300m and base is 900m |
|
Verification:
Area of triangle = 1/2*900*300 = 900*150 = 135000
Cost of cultivation = 135000*36.72/100 = 49572
which is as given in the problem
6.7.3 Area of a
quadrilateral
|
We have seen that a diagonal of
a quadrilateral cuts the quadrilateral in to 2 triangles. We shall use this Property to
calculate the area of a quadrilateral, as we already know how to calculate
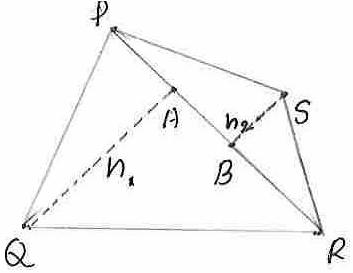
the area of a triangle. Let PQRS be the quadrilateral. Draw the diagonal PR. Draw a
perpendicular (QA= h1) to PR
from vertex Q. Draw another perpendicular (SB=h2)
to PR from vertex S. h1 and h2 are altitudes of Area of Area of
= ½(PR*
h1)+ ½(PR* h1) = 1/2*PR* (h1+h2)
sq units
1/2 * diagonal * sum of altitudes of the two triangles with diagonal as base |
|
6.7.4 Types of
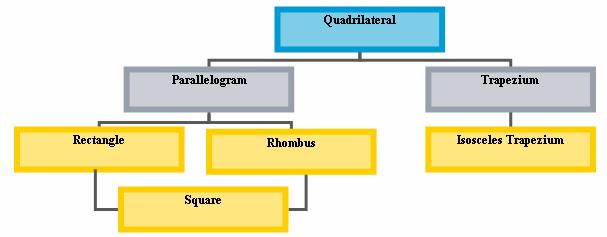
quadrilaterals
Depending on the shape of quadrilateral, they are
classified as follows:
|
Type |
Main(Basic) Property of
quadrilateral |
Figure |
Relationship between Sides |
Relationship between Angles |
Relationship between Diagonals |
|||
|
Parallelogram |
Both pairs
of opposite sides are parallel |
|
1.Both pairs of opposite
sides are parallel 2.Both pairs of
opposite sides are equal |
1.Oppopsite angles are equal. 2. Sum of any two consecutive angles = 1800 |
1.Diagonals divide the parallelogram in to two congruent
triangles 2. Diagonals bisect each other |
|||
|
Trapezium |
Only
one pair of opposite sides are parallel |
|
A pair of opposite sides are parallel |
Pairs of consecutive angles at the end points of
the two non parallel sides are supplimentary |
|
|||
|
Isosceles
Trapezium |
One
pair of opposite sides are parallel and non parallel sides are equal |
|
1.A pair of opposite sides are parallel 2. Non parallel sides are equal. |
1.Pairs of consecutive angles at the end points of
the two non parallel sides are suplementary 2.Pairs
of consecutive angles at the end points of the two parallel sides are equal. |
Diagonals are equal |
|||
|
Rectangle |
Both pairs
of opposite sides are parallel and all
angles are right angle |
|
1.Opposite sides are equal 2. Both pairs of opposite sides are parallel |
All angles are equal and are right angles |
1.Diagonals divide the rectangle in to two Equal
triangles 2. Diagonals are equal 3 Diagonals bisect
each other |
|||
|
Rhombus |
All
sides are equal and both pairs
of opposite sides parallel |
|
1. All sides are equal 2. Both pairs of opposite
sides are parallel |
1.Oppopsite angles are equal. 2.Sum of any two consecytive angles = 1800 |
1.Diagonals divide the rhombus in to two congruent
triangles 2. Diagonals bisect each other. 3. Diagonals are | to each other. |
|||
|
Square |
All
sides are equal and all
angles are right angles |
|
1 All sides are equal 2.Both pairs of opposite
sides are parallel |
All angles are
equal and right angles |
1.Diagonals
divide the sqaure in to two congruent triangles 2.
Diagonals are equal. 3. Diagonals bisect each other. 4. Diagonals are | to each other. |
Note : Why mothers
and grandmothers cut burfies in the shape of parallelogram and not in rectangles?
Because they could cut more pieces from the same spread of sweet
preparation (Did they study Geometry?)
The reason we will learn later (Section6.8.2)
is that the area of a rectangle (base*another side) is greater than the area of
parallelogram (base*height) when their sides are of same measures.
The hierarchy of different types of quadrilaterals can
be represented by the following chart:
|
|
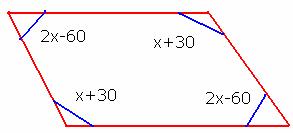
6.7.4 Problem 1: Two consecutive
angles of a parallelogram have measures, (x+30) and (2x-60) respectively. Find
the measures of all angles.
Solution:
|
We know that in a parallelogram,
sum of any two consecutive angles = 1800.
Hence the angles are 100,80,100
and 80 |
|
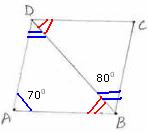
6.7.4 Problem 2: In a
parallelogram ABCD, ![]() DAB= 700,
DAB= 700, ![]() DBC = 800 Find
DBC = 800 Find ![]() CDB and
CDB and ![]() ADB.
ADB.
Solution:
|
We know that in a parallelogram,
sum of any two consecutive angles 1800.
i.e. 700+
Since BA || CD, corresponding
angles are equal
Since in a parallelogram
opposite angles are equal, So the angles are 700,
1100, 700 and 1100. |
|
6.7.4 Problem 3: The ratio of two sides of a parallelogram is 3:5
and the perimeter is 48cm. Find the sides of the parallelogram.
Solution:
|
We know that in a parallelogram
Perimeter = sum of four sides = 2*(sum of any 2 adjacent
sides) Since it is given that the perimeter
= 48cm
Since the ratio of adjacent
sides = 3:5, let the sides be 3x and 5x
So the lengths of adjacent sides
are 9cm and 15cm Hence the sides are 9cm, 15 cm, 9
cm and 15cm. Verification: Perimeter = sum of all sides =
9+15+9+15 = 48cm, which is as given in the problem and hence our solution is
correct. |
|
6.7 Summary of learning
|
No |
Points
to remember |
|
1 |
Area of quadrilateral = 1/2 * diagonal
* sum of altitudes of the 2 triangles with diagonal as base |
Additional Points:
Heron’s
formula for calculation of area of a triangle:
|
If a, b and c are measures of
the three sides of a triangle then area can also be calculated by using the
formula: Area = Where s = (a+b+c)/2 (semi
perimeter of the circle) Note: Though this has come to be known
as Heron’s formula, ‘Bhaskara’ had provided
the proof of this in his book (‘Leelavati’- shloka 169). |
|
6.7.2 Problem 2: Find the area of a triangular
park whose sides are 18m, 24m and 30m. Also find the length of the altitude
corresponding to the largest side of the triangle.
Solution:
Let a=18, b=24 and c=30.
![]() s = (a+b+c)/2 = 36
s = (a+b+c)/2 = 36
![]() Area =
Area =![]()
![]() =
= ![]() =
= ![]() = 216
= 216
Since the largest base is 30, let the height on
this base be h.
We have 216 = 1/2*30*h (![]() area of a triangle = (1/2)*base*height)
area of a triangle = (1/2)*base*height)
![]() h = 216/15 = 14.4m
h = 216/15 = 14.4m
Verification:
Area of triangle = 1/2*30*14.4 = 216
Note: Heron’s formula is very helpful if
we have to calculate the area of a quadrilateral given its sides and a diagonal,
as in the problem given below.
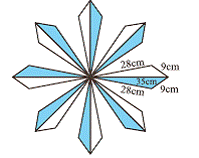
6.7.2 Problem 3: A floral
design on a floor is made up of 8 tiles which are quadrilaterals.
Its sides are 9cm, 28cm, 9cm and 28cm and it’s diagonal is 35cm as shown in the
adjoining figure. Find the cost of polishing the tiles at the rate of 50paisa
per sq.cm.
Solution:
|
Let us
calculate the area of each tile Area of
a tile = area of quadrilateral = 2*area of the triangle The
sides of the triangle are a=28, b=9 and c=35.
|
|