6.9 Circles- Part 1

 

 

In the previous lessons we learnt about straight lines, figures  formed by straight lines. Are there  figures other than these?

What about our universe?, The earth goes around in the ecliptic path. Moon follows a circular path to go around earth.

 

We also come across objects such as coin, wheels, cycle tires, rings. They are all in circular shapes. In this lesson we shall study their properties.

 

6.9.1 Definitions

 

           Definitions:

 

Figure

Definition

 

 

 

 

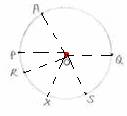
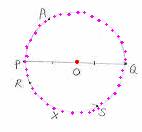
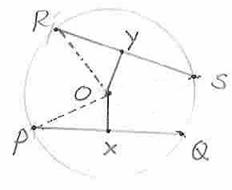
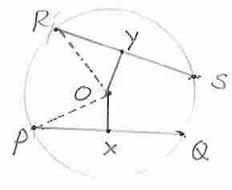
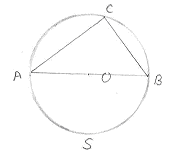
‘Circle’ is a closed curve on a plane, with every point on the curve at equal distance from a fixed point. The fixed point is called center of the circle and is denoted by O. In the figure, points P,A,Q,R and S are at same distance from O.

‘Radius’ is the line segment joining the centre of the circle with any point on the circle. It is denoted by r.  There are many radii. In the figure OP,OQ,OA  are radii.  OP=OA=OQ.

‘Chord’ is a line segment joining any two points on the circle. In the figure, AQ and RS are two chords.

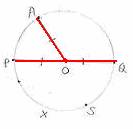
‘Diameter’ is the line segment passing through the center of the circle and having its end points on the circle. It is denoted by d.

It is the longest chord of the circle. In the figure, PQ is the diameter and it passes through the center O. There are many diameters

Note that d=PQ= PO+OQ =r+r =2r

‘Circumference’ is the distance around the circle (perimeter of the circle). In the figure, the distance measured from point P to P through the points A, Q, S and R is the circumference.

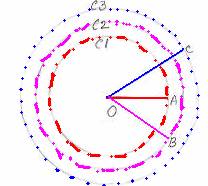
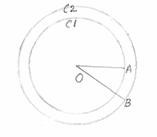
Circles having same center but different radii are called ‘Concentric circles’.

 

 

 

 

C1, C2 and C3 are 3 circles with different radii OA, OB and OC but with same center O.

 

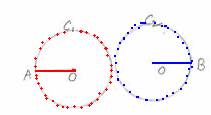
Different circles having same radii are called ‘Congruent circles’.

 

 

 

C1 and C2 are 2 circles having same radii OA(OA=OB) but with different centers.

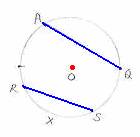
 ‘Arc’ is a part of the circle. The curve RS is an arc.

 

‘Segment’ is a part of the region, bounded by the chord and the arc. In the figure, RXSR is a segment.

A chord divides the circle into two parts. Correspondingly we have two segments: minor and major segments.

ASBA is a ‘minor’ segment.

(Region bounded by the minor arc ASB and the chord AB)

 

 

 

Chord AB is the diameter.

ASBOA and ACBOA are ‘semi’ circles (regions bounded by equal arcs ASB,ACB and the diameter AB).

 

 

 

ASBA is a ‘major’ segment.

(Region bounded by the larger(major) arc ASB and the chord AB)

 

 

 

6.9.2 Properties (Theorems):

 

6.9.2.1. In a circle, the perpendicular from the center to the chord bisects the chord.

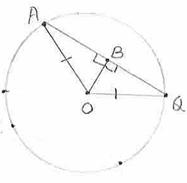
Data: In the adjoining figure, O is the center, AQ is the chord and OB is perpendicular to AQ.

To Prove: AB=BQ

 

Solution:

Steps

Statement

Reason

 

Consider the OAB and OQB

1

OA = OQ

Radii of the circle

2

OBA =OBQ=900

It is given that OB is perpendicular to AQ

3

OB is the common side

 

4

OAB  OQB

SAS postulate

5

AB=BQ

Corresponding sides are equal

 

Conversely, the line joining the mid point of a chord to the center is perpendicular to the chord

Exercise: Prove yourself (Proof is similar to the above)

 

6.9.2.2. Equal chords of a circle are equidistant from the center

Data: In the adjoining figure, O is the center, PQ and RS are 2 equal chords. OX and OY are perpendiculars to PQ and RS respectively.

To Prove: OX=OY

Construction: Join OP and OR

 

Solution:

Steps

Statement

Reason

 

Consider the OPX and ORY

1

2PX=PQ

The perpendicular OX bisects the chord PQ

2

2RY=RS

The perpendicular OY bisects the chord RS

3

PQ=RS

Given that chords are equal

4

2PX=2RY

i.e. PX=RY

Substitute vales from Step1 and Step2 in Step3

5

OP =OR

Radii of the circle

6

PXO =OYR=900

 

4

PXO  RYO

SAS postulate

5

OX=OY

Corresponding sides are equal

 

6.9.2.3.  Chords of a circle which are equidistant from the center are equal.

This property is converse of 6.9.2.2.

Data: In the adjoining figure, O is the center, PQ and RS are the chords.

OX and OY are perpendicular to PQ and RS respectively and OX=OY

 

To Prove: PQ=RS

 

Construction: Join OP and OR

 

Exercise:  Follow the steps described above (6.9.2.2) to prove that  PXO  RYO and then show that PX=RY

 

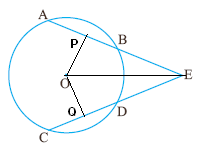
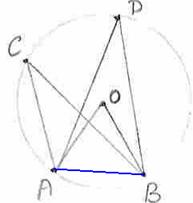
6.9.2 Problem 1: In the adjoining figure AB and CD are equal chords of a circle whose center is O, when produced these chords

meet at E. Prove that EB=ED

 

Construction: Draw Perpendiculars to AB and CD to meet AB at P and CD at Q, Join OE

Steps

Statement

Reason

1

AP =1/2AB

Perpendicular bisects the chord

2

CQ= 1/2CD

Perpendicular bisects the chord

3

AP=CQ

AB=CD(given)

4

OPB =OQD = 900

Construction

5

OP =OQ

Equal chords are equidistant.

6

OE  is common

Construction

7

OPE   OPB

RHS postulate on congruence

8

PE=QE

Corresponding sides are equal

9

AP+PE =CQ+QE

Step 3 and 8

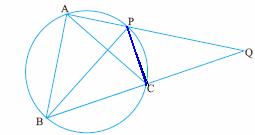
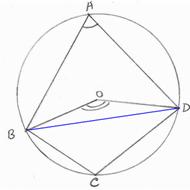
6.9.2 Theorem (Inscribed Angle Theorem): In any circle, the angle subtended by an arc at the center of the circle is double the

angle subtended by the same arc at any point on the remaining part of the circle.

 

Data: In the adjoining figure, O is the center of the circle. AOB is the angle subtended by the arc AXB, at the centre of the circle.

APB is the angle subtended by the same arc at any point (P) on the remaining part of the circle.

To prove: AOB = 2APB

Construction: Extend PO to meet the circle at D

 

Proof:

Steps

Statement

Reason

1

OA = OP

Radii of the circle

2

OPA = OAP

OAP is an isosceles triangle

3

AOD =OAP+OPA

Exterior angle in a triangle (AOP) is equal to the sum of two interior angles.

4

= 2OPA

Substitute result of Step 2 in Step 3.

5

OB = OP

Radii of circle

6

OBP = OPB

OBP is an isosceles triangle

7

BOD =OBP+OPB

Exterior angle in a triangle (BOP) is equal to the sum of two interior angles.

8

= 2OPB

Substitute the result from Step 6 in Step 7

9

AOD+ BOD=2OPA+2OPB

=2(OPA+OPB)= 2APB

From steps 3,4,7 and 8

10

AOB =2APB

AOB=AOD+ BOD

 

Corollary : Angle in a semi circle is a right angle

In the adjacent figure AB is radius and ACB is the angle at semi circle,

we are required to prove that ACB = 900

 

 

Hint:  

From the above theorem, 2 ACB = AOB

Since AOB is a straight line, it follows that  AOB = 1800

Hence  ACB = 900

 

Theorem: Prove that inscribed angles in the same segment of a circle are equal

 

Given: A and B are points on the circle. ACB and ADB are the inscribed angles and AOB is the central angle

To Show: ACB= ADB

 

Steps

Statement

Reason

1

AOB= 2ADB

Central angle is double the inscribed angle of the same segment (arc) AB

 

2

AOB= 2ACB

Central angle is double the inscribed angle of the same segment (arc) AB

 

3

 2ACB= 2ADB

Equating results from steps 1 and 2

 

 

4

i.e. ACB= ADB

 

 

Converse of the above theorem is the below mentioned theorem:

Theorem: (Proof not provided)

If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the segment,

then the four points lie on the same circle.(In the above figure ABCD will be concyclic, if ACB= ADB)

The proof is by logical reasoning. (Making an assumption that the theorem is not true and then proving that assumption made is wrong)

 

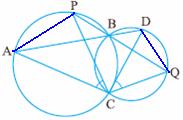
6.9.2 Problem 2: Prove that the APC and DPB are equiangular in the adjoining figure

Also prove that the product of their segments is equal

Given: AC and BD are 2 chords of the same circle

To Show: APC and DPB are equiangular and PC*PD =BP*PA

 

Steps

Statement

Reason

1

ACD = ABD

Inscribed angles on the circle formed by the same segment (arc) AD

2

CAB = CDB

Inscribed angles on the circle formed by the same segment (arc) BC

3

CPA = BPD

Vertically opposite angles

4

APC |||DPB

 AAA postulate on similarity

5

AC/BD = PD/PA =PB/PC

corresponding sides are proportional

6

PC*PD =PA*PB

 

         Note  This proves the  following theorem

Theorem : If two chords of a circle intersect internally or externally then the product of the lengths of their segments are equal.

On the lines of 6.9.2 Problem 2 we can prove the above theorem when P is outside the circle also.

 

6.9.2 Problem 3: In the adjoining figure, AB and BC are diameters of two circles intersecting at B and D. Show that A, D and C are collinear.

 

Given: AB and BC are diameters.

To Show: ADC = 1800

Steps

Statement

Reason

 

1

APB = 1800

Angle on the straight line

2

APB = 2ADB

Central angle is double the inscribed angle of the same segment (arc) AB

2

 2ADB = 1800

From Step1 and Step 2

3

i.e. ADB = 900

 

4

BQC = 1800

Angle on the straight line

5

BQC = 2BDC

Central angle is double the inscribed angle of the same segment (arc) BC

6

 2BDC = 1800

From Step4 and Step 5

7

i.e. BDC = 900

 

8

ADB+BDC = 1800

From Step 3 and Step 7

 

6.9.2 Problem 4: In the adjoining figure, two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are

drawn to intersect the circles at A,D and P,Q respectively. Prove that ACP = QCD

 

Steps

Statement

Reason

1

ACP  = ABP

Angle on the circle on the same chord AP

 

2

ABP = DBQ

Vertically opposite angles.

 

3

DBQ = DCQ

Angle on the circle on the same chord DQ

 

4

ACP = QCD

From Step 1,2,3

 

6.9.2 Problem 5: In the adjoining figure, the bisector of B of an isosceles triangle ABC with AB=AC meets the circumcircle of ABC at P.

If AP and BC produced meet at Q, prove that CQ=CA

 

Construction: Join CP.

Steps

Statement

Reason

 

1

ABC = 2CBP

BP is bisector of ABC

2

CBP=CAP

The chord PC subtends same angle

3

ABC = 2CAP

Step 1 and 2

4

BCA = CAQ+CQA

Exterior angle in a  is sum of interior angles

5

CQA = BCA-CAP

Simplification

6

= ABC-CAP

BCA =ABC as AB=AC

7

=2CAP-CAP = CAP

Step 3

8

CQ=CA

Step5,6(Angles on the base AQ are equal)

      

         Construction of Circle:

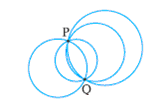
1. Can we construct a unique circle given just a point?

No, because we can construct several circles passing through a point

 

2. Can we construct a unique circle given two non-collinear points?

No, because we can construct several circles passing through two points

Note in the adjacent figure through P and Q we can construct several circles

 

3. Can we construct a unique circle given three non-collinear points?

yes. We could do that and steps are as follows:

 

Method:

Steps

construction

1

Take 3 points A, B, C

 

 

2

Join AB, BC

 

 

3

Construct perpendicular bisectors to AB,BC(Refer 6.4.3)

 

 

4

Let these bisectors meet at S

 

 

5

With SA as radius draw circle

        Note that this circle touches B and C as well; In fact this circle is circumcircle of  ABC and S is its Circumcenter

 

Note:  Refer Section 6.4.3 to know more about circumcircle.

Since SA=SB=SC it is proved that S is the center of circle, passing through points A,B,C.

This proves that there is only one circle which passes through three points which are not collinear.

4. Construction of a circle (need not be unique) given two points.

 

Method:

Let A and B are the given two points.

Let C be a point on the plane such that A, B and C are non-collinear.

Draw perpendicular bisectors of AB and BC as above and let they meet at S.

The circle with S as center and SA as radius passes through B.

 

6.9.3 Cyclic quadrilateral

 

Definition: A quadrilateral whose vertices lie on a circle is called a ‘cyclic quadrilateral’. It is an inscribed (inside a circle) quadrilateral.

 

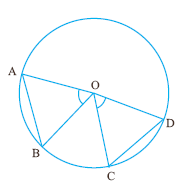
6.9.3 Theorem:  Opposite angles of a cyclic quadrilateral are supplementary (i.e. their sum is 1800).

 

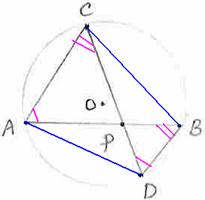
Data:  ABCD is a cyclic quadrilateral and O is the center of circle.

To prove: BAD + BCD = 1800 and ABC +ADC = 1800.

Construction: Join OB and OD. Note that BOD is the central angle and BAD is the inscribed angle.

 

Proof:

Steps

Statement

Reason

1

BAD = 1/2  of BOD

Inscribed angle is half the angle at center

 

 

2

BCD = 1/2 of reflex BOD

Inscribed angle is half the angle at center

 

 

3

BAD +BCD = 1/2 BOD +  1/2 of reflexBOD =

1/2(BOD+ reflexBOD) = 1/2(3600) = 1800

(BOD+ reflexBOD) is the complete angle at the center and is equal to  = 3600

 

 

4

Similarly ABC +ADC = 1800

 

 

This proves that opposite angles of a cyclic quadrilateral are supplementary (i.e. their sum is 1800).

Note :

When we join BD, then we get two segments:BAD as a major segment and BCD as a minor segment on the same chord BD.

 

They are also referred as ‘alternate segments’

The above theorem can be restated as

Theorem: Angles in the alternate segments of a circle are supplementary.

 

Converse of above Theorem :( Proof not provided): If the opposite angles of a quadrilateral are supplementary, then it is cyclic.

The proof is by logical reasoning. (Making an assumption that the theorem is not true and then proving that assumption made is wrong)

 

6.9.3 Problem 1:  Prove that the exterior angle of a cyclic quadrilateral is equal to its interior opposite angle.

 

Given: ABCD is a cyclic quadrilateral. DCE is the exterior angle

To prove: BAD =DCE

 

Steps

Statement

Reason

1

BAD+ BCD = 1800

Opposite angles of a cyclic quadrilateral is supplementary

2

BCD + DCE = 1800

Linear pair or adjacent angles on a straight line

3

 BAD+ BCD = BCD + DCE

BAD =DCE

Subtract BCD from both sides

       This proves that the exterior angle of a cyclic quadrilateral is equal to its interior opposite angle.

 

6.9.3 Problem 2:  Prove that when a parallelogram is inscribed in a circle it becomes a rectangle

 

Given: ABCD is a parallelogram and ABCD is a cyclic quadrilateral

To prove: ABC = BCD = ADC = DAB = 900

 

Steps

Statement

Reason

1

BAD+ BCD = 1800

Opposite angles of a cyclic quadrilateral is supplementary

 

 

2

BAD = BCD

Opposite angles in a parallelogram are equal.(Refer 6.7)

 

 

3

BAD =BCD =900

From step 1,2


This proves that when parallelogram ABCD is inscribed in a circle it becomes a rectangle

 

6.9.4 Construction of a cyclic Quadrilateral

 

Steps to be followed (general):

 

Note: We need to draw a circle which passes through all the 4 vertices of a quadrilateral. We have learnt that the circumcircle of a triangle

passes through all the 3 vertices of a triangle. So our problem will be solved if we can construct a circumcircle and then locate a point on

that circle which is the fourth vertex of the quadrilateral.

 

Step 1: Construct a Triangle with the given data

Step 2: Bisect any two sides of this Triangle (To find the Circumcenter)

Step 3: Join these bisectors to meet at origin O

Step 4: With O as origin, draw a circle passing through 3 points of the triangle drawn in Step1

Step 5: Cut an arc of given length on the circle, to locate the 4th point.

 

Note: To construct a triangle we need three values (elements). They could be any of the following:

1. Length of three sides

2. Length of one side and two angles on this line

3. Length of two sides and the included angle

 

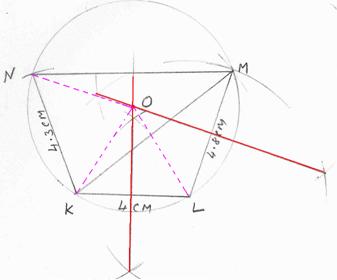
6.9.4 Problem 1:

Construct a cyclic quadrilateral KLMN with KL = 4cm, LM = 4.8cm, KM = 6.8cm and KN = 4.3cm.

Steps:

1. Construct the triangle KLM as follows:

       (i)  Draw the line KL=4cm.

       (ii)  From K, draw an arc of radius of 6.8cm. From L, draw       

             another arc of radius 4.8cm. Let they meet at M.

       (iii) Join KM and LM to form the triangle KLM.

 

2. Bisect the lines KL and LM and extend the bisector lines to meet at point O

 

3. With O as origin, draw a circle passing through the points K, L and M

 

4. From K, draw an arc of radius 4.3cm to cut the circle at point N

 

5. Draw the quadrilateral KLMN

 

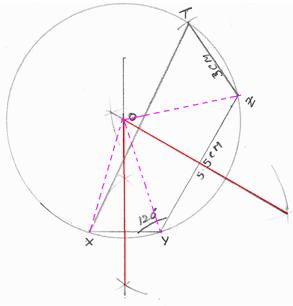
6.9.4 Problem 2:

 

Construct a cyclic quadrilateral XYZT with XY= 2.5cm, YZ=5.5cm, ZT=3cm and XTZ = 600.

 

Note: Since XYZT is a cyclic quadrilateral, the opposite angles XTZ and XYZ are supplementary and hence XYZ= 1200 .

 

Steps:

1. Construct the triangle XYZ as follows:

     (i)  Draw the line XY=2.5cm.

     (ii)  From Y, draw a line at an angle 1200 with XY. Draw an arc of radius 5.5cm  

          from Y to cut this line at Z

     (iii) Join XZ to form the triangle XYZ.

 

2. Bisect the lines XY and YZ and extend the bisector lines to meet at point O

 

3. With O as origin draw a circle passing through the points X, Y and Z

 

4. From Z, draw an arc of radius 3cm to cut the circle at point T

 

5. Draw the quadrilateral XYZT.

 

 

6.9 Summary of learning

 

 

 

No

Points to remember

1

In a circle, the perpendicular from the center to the chord bisects the chord.

2

Equal chords of a circle are equidistant from the center

3

Chords of a circle which are equidistant from the center are equal.

4

In any circle, the angle subtended by an arc at the center is double the angle subtended by the same arc at any point on the remaining part of the circle

5

Opposite angles of a cyclic quadrilateral are supplementary (i.e. their sum is 1800).

 

 

Additional points:

 

6.9.2.4. Equal chords of a circle subtend equal angles at the center

 

Proof:

Steps

Statement

Reason

 

Consider the AOB and COD

1

OA = OD

Radii

 

2

OB = OC

Radii

 

3

AB = CD

Given

 

4

AOB COD

SSS postulate

 

5

AOB =COD

Corresponding angles are equal

 

6.9.2.5. If the angles subtended by chords of a circle at the center are equal then these chords are equal

Note: This is converse of 6.9.2.4.

Proof:

Steps for the proof are similar to the given in section 6.9.2.4, except that in the third step, use the given data that AOB =COD

and then by SAS property, prove that the triangles are congruent and hence show AB=CD.

 

Note: There is one and only one circle passing through 3 non-collinear points.

 

6.9.5 Area of circle

 

The length around a circle or the perimeter of a circle is called its ‘circumference’.

If  ‘r’ is the radius of any circle, then the formula for the circumference is c = 2r , where  is a constant.

We use its approximate value of 22/7 in all our calculations.

The area of a circle = r2.

Observation:

 

When we discuss , the names which come to our mind are  the mathematicians Aryabhata and Bhaskaracharya

 

1)     Aryabhatta of 5th century AD was the first one to give approximate value of  to 4 correct decimal places (3.1416).

 

           His formula is:

          The approximate circumference of a circle of diameter 20000 units is got by adding 62000 to the result of 8 times the sum of 100 and 4.

          Circumference = 62000+ 8(100+4) = 62832; Diameter = 200

           = circumference ÷ diameter = 62832 ÷ 20000= 3.1416

         

2)     Bhaskarachary’s formula ( Lilavati, Shloka  202)

The circumference (approximate value) of a circle is got by multiplying its diameter by 3927 and then dividing the product by1250.

For simpler calculations, the circumference of a circle is got by multiplying its diameter by 22 and then dividing the product by 7.

 = circumference ÷ diameter = 3927 ÷ 1250 = 3.1416

For simpler calculations,  = 22/7

 

6.9.5 Problem 1: Area of two circles are in the ratio of 25:36. Find the ratio of their circumferences.

 

Solution:

If r and R are the radii of the two circles then their areas are r2 and R2.

It is given that r2:R2= 25:36

 r2:R2= 25:36 = 52:62

 r:R = 5:6

 2r:2R = 2*5:2*6 = 5:6

 

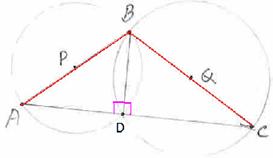
6.9.5 Problem 2: A well of diameter 150cm has a 30cm wide parapet running around it. Find the area of the parapet.

 

Solution:

Since the diameter of the well is 150cm, it’s radius = 75cm.

Well can be imagined as a circle C1 having of radius OA(r) = 75cm as shown in the adjoining figure.

C2 is another circle around the well with a radius of OB(R) = (75+30)cm = 105cm

Area of the circle C2 = R2 = 22/7*105*105 = 34650 sq.cm.

Area of the circle C1 = r2 = 22/7*75*75     = 17678.6 sq.cm.

 Area of the parapet = R2-r2= 34650-17678.6 = 16971.4 sq.cm.

= 1.7 sq.m.

 

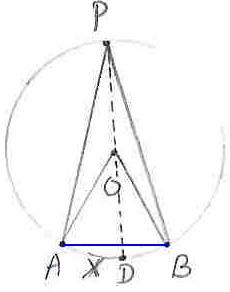
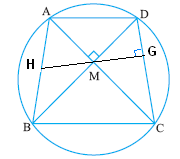
Brahmagupta’s theorem:

A cyclic quadrilateral in which the diagonals are perpendicular to each other, the perpendicular through the point of intersection of the

diagonals to one of the sides, bisects the opposite side. Though we do not know his proof, our proof based on what has been learnt

so far is as follows.

Given: ABCD is a cyclic quadrilateral. ACBD, MG CD, GM produced meets AB at H.

To prove: AH=BH

Steps

Statement

Reason

 

 

 

 

 

 

 

Consider the MDG  and MAH

1

MDG + GMD = 900

MGD = 900 (given) and sum of angles in a triangle is 1800

2

AMH + BMH = 900

Given that diagonals are perpendicular to each other

3

BMH =GMD

Vertically opposite angles

4

MDG = AMH

Steps 1,2,3

5

BDC = MDG = BAM

Inscribed angles on same chord BC

6

BAM = AMH

Steps 4,5

7

AH = HM

Step 6 (AMH is an isosceles triangle)

 

Consider the MCG  and MBH

8

MCG + GMC = 900

MGC = 900(given) and sum of angles in a triangle is 1800

9

AMH + BMH = 900

Given that diagonals are perpendicular to each other

10

AMH =GMC

Vertically opposite angles

11

MCG = BMH

Steps 8,9,10

12

ABD = MCG = ABM

Inscribed angles on same chord AD

13

ABM = BMH

Steps 11,12

14

BH = HM

Step 6 (AMH is an isosceles triangle)

15

AH = BH

Steps 7 and 14