2.19 ™¿U¿ ∏¿´ƒ√P¿g¿tU¿º¿ƒ(Quadratic Equations):
Cdƒ£¿£¿ƒ ™¿ƒ∫¡®s¡g¿v¿ Ai¿ƒƒz¿Þz¿∞Ë P¿t£¿£¿ƒþ
P…∆ÆËƃ ßv¿€ΩP… ¨ƒAz¿ ∫¿Æ™¿≈ ®¡tU¿º¿£¿ƒþ v…U…Ai¿ƒƒv¡€£…. v…U…z¿ ®¡tU¿º¿∞Ë Czs¿z¿µ¿÷jAz¿
P¿t£¿ ®¡tU¿º¿£¿ƒþ v¿ƒAq¿j∏¿ƒv¡€£…. v…U…z¿ ®¡tU¿º¿ ™¿U¿™¿ƒ∆Æz¿ 4 g¿µ¿÷jAz¿ P¿t£¿ P¿ƒz¿ƒg…U¿º¿£¿ƒþ, 6 ®¡tU¿ΩAz¿ ±¿Æ£¿£¿ƒþ, MAz…∆Az¿jAz¿ P¿t£¿
g¿x¿z¿ P…∆q…, P¿t£¿ g¿x¿z¿ ®¡™¿≈l, ™¿ƒv¿ƒ€ P¿t£¿ ©ÆË£¿ƒþ v¿ƒAq¿j∏¿ƒv¡€£….
GΩz¿ MAz¿ƒ ®¡t¢Az¿ P¿t£¿£¿ƒþ P…∆Az¿g…, ßv¿€ΩP… ¨ƒAz¿ Mlƒ÷ Jµ¿ƒ÷ ®¡tU¿º¿£¿ƒþ
v…U…Ai¿ƒƒv¡€£…? (∞√Ø¡™¿w: ±…∆Ë√P¿ 71)
™…ƒ√∞£¿ ∏¿™¿ƒ∏… ©r∏¿ƒ™¿ D∏… Ez…Ai…ƒ√?
§d f√™¿£¿z¿∞Ë Jz¿ƒj∏¿ƒ™¿ P…º¿V£¿
∏¿™¿ƒ∏…ÂU… Gv¿€g¿ U…∆v…€√?
∏¿™¿ƒ∏…Â: §√™¿≈, §™¿ƒ‰ ∏…þ√ªv¿g¿ƒ Mn÷U… MAz¿ƒ •¿Ê™¡∏¿P…Ã
∫…∆√U¿Æƒ ßAi¿ƒ∏¿ƒw€√j. D∫¡g¿P¡ÃV Mlƒ÷ 480g¿∆.
RZ¡U¿ƒv¿€z…Az¿ƒ Ø…P¿Ã ∫¡Q¢j. Dz¿g… P…∆£…Ai¿ƒ P¿Îtz¿∞Ë 8 ™¿ƒA¢
§™¿ƒ‰ ∏…þ√ªv¿g¿ƒ •¿Ê™¡∏¿P…à ∫…∆√U¿∞ÆË. E™¿g¿ƒ ®¡g¿¢z¿ƒðz¿jAz¿, •¿ÊwAi…∆ß‚g¿∆
D∫¡g¿P¡ÃV 10g¿∆. ∫…a—U… P…∆q¿®…√P¡¨ƒv¿ƒ. ∫¡U¡z¿g… •¿ÊwAi…∆ß‚g¿∆
P…∆£…U… P…∆l÷ ∫¿t Jµ¿ƒ÷?
£¡™¿≈ FU¡U¿Ø…√ P…º¿V£¿ P…Æ™¿≈ ∏¿™¿ƒ∏… ©r∏¿ƒ™¿≈z¿£¿ƒþ P¿∞wz…ð√™…:
1. MAz¿ƒ ™¿U¿z¿
∏¿ƒv¿€º¿v… 60´ƒ√lgÔ Dz¿g… Cz¿g¿ ߢAi¿ƒ Gz¿ð Jµ¿ƒ÷?
P¿Ê™¿ƒ: ™¿U¿z¿ MAz¿ƒ ߢ: ëxí DVg¿∞. DU¿
∏¿ƒv¿€º¿v… = 4x
![]() Ý4x =60
Ý4x =60
x =15 ´ƒ√lgÔU¿º¿ƒ
F j√w g…√S¡v¿‰P¿ ∏¿´ƒ√P¿g¿tP…à MAz…√ •¿j∫¡g¿´g¿ƒv¿€z….
F •¿j∫¡g¿™¿£¿ƒþ ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆Æ J£¿ƒþv…€√™…. E∞Ë 15, 4x = 60
ÝJ£¿ƒþ™¿ ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆Æ.
2. MAz¿ƒ ™¿U¿z¿
´π€√t 25 Z¿z¿g¿ ´ƒ√lgÔU¿º¡z¿g… Cz¿g¿ MAz¿ƒ ߢAi¿ƒ Gz¿ð Jµ¿ƒ÷?
P¿Ê™¿ƒ: ™¿U¿z¿ MAz¿ƒ ߢAi¿ƒ Gz¿ð ëxí DVg¿∞. DU¿ D
™¿U¿z¿ ´π€√t = x2
x2 = 25 =5*5
![]() Ýx=5 ´ƒ√lgÔU¿º¿ƒ
Ýx=5 ´ƒ√lgÔU¿º¿ƒ
Dz¿g… 25 = -5*-5 JAz¿∆ DU¿ƒv¿€z….Ý ![]() x= -5 F ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆Æ™¿« DVz¿ƒð x2 = 25£¿ƒþ v¿»¶€ •¿r∏¿ƒv¿€z…. Dz¿ðjAz¿ x =
x= -5 F ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆Æ™¿« DVz¿ƒð x2 = 25£¿ƒþ v¿»¶€ •¿r∏¿ƒv¿€z…. Dz¿ðjAz¿ x = ![]() 5Ý F ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿ƒ.
5Ý F ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿ƒ.
™¿U¿z¿ ®¡∫¿ƒ´£¿ Gz¿ð Iƒt ∏¿AS…ÂAi¿i¡U¿Æƒ ∏¡zs¿Â´ÆË™¡z¿ðjAz¿ x = -5 £¿þ ∏¿´ƒ√P¿g¿tz¿ •¿j∫¡g¿™¡V v…U…z¿ƒP…∆º¿ƒÓ™¿≈¢ÆË.
™¡ÂS…Â: D™¿ÂP¿€ •¿z¿z¿ W¡v¿ 2 DVg¿ƒ™¿ ∏¿´ƒ√P¿g¿t™¿£¿ƒþ ™¿U¿ ∏¿´ƒ√P¿g¿t (quadratic equation) J£¿ƒþv…€√™….
x2 = 25 Ez¿£¿ƒþ
x2 - 25 =0 JAz¿∆ ßg…Ai¿ƒ∫¿ƒz¿ƒ (KP… ™¿ƒv¿ƒ€ ∫…√U… ?)
F ∏¿´ƒ√P¿g¿tz¿∞Ë Z¿g¡P¿Îg¿ x £¿ W¡v¿ 2
™¿i¡v¿Ê´z…. ™…∆z¿Æ W¡v¿z¿ Z¿g¡P¿Îg¿´ÆË.(bx JAß CA±¿´ÆË.)
™¡ÂS…Â:
1. ax2 +c = 0 ∏¿´ƒ√P¿g¿tz¿
g¿∆•¿z¿∞Ë ™¿ÂP¿€•¿r∏¿ß∫¿ƒz¡z¿ ∏¿´ƒ√P¿g¿t™¿£¿ƒþ ±¿ƒz¿Þ ™¿U¿ ∏¿´ƒ√P¿g¿t (pure quadratic
equation)J£¿ƒþ™¿g¿ƒ. a ™¿ƒv¿ƒ€ c U¿º¿ƒ ™¡∏¿€™¿
∏¿AS…ÂU¿º¡Vz¿ƒð, a ![]() 0 DVg¿ƒv¿€z….
0 DVg¿ƒv¿€z….
2. a, b ™¿ƒv¿ƒ€ c U¿º¿ƒ
™¡∏¿€™¿ ∏¿AS…ÂU¿º¡Vz¿ƒð a ![]() 0, b
0, b ![]() 0,Ý DVg¿ƒ™¿ ax2
+bx+ c = 0 g¿∆•¿z¿∞Ë
™¿ÂP¿€•¿r∏¿ß∫¿ƒz¡z¿ ∏¿´ƒ√P¿g¿t™¿£¿ƒþ ´ƒ±¿Ê™¿U¿ ∏¿´ƒ√P¿g¿t (Adfected
Ýquadratic
equation) J£¿ƒþ™¿g¿ƒ.Ý E∞Ë b=0 Dz¿g…, Cz¿ƒ ±¿ƒz¿Þ ™¿U¿ ∏¿´ƒ√P¿g¿t™¡U¿ƒv¿€z….
0,Ý DVg¿ƒ™¿ ax2
+bx+ c = 0 g¿∆•¿z¿∞Ë
™¿ÂP¿€•¿r∏¿ß∫¿ƒz¡z¿ ∏¿´ƒ√P¿g¿t™¿£¿ƒþ ´ƒ±¿Ê™¿U¿ ∏¿´ƒ√P¿g¿t (Adfected
Ýquadratic
equation) J£¿ƒþ™¿g¿ƒ.Ý E∞Ë b=0 Dz¿g…, Cz¿ƒ ±¿ƒz¿Þ ™¿U¿ ∏¿´ƒ√P¿g¿t™¡U¿ƒv¿€z….
´ƒ±¿Ê™¿U¿ ∏¿´ƒ√P¿g¿tP…à Gz¡∫¿g¿u…: 3x2 -5x-16=0
Gz¡∫¿g¿u…: 3x2 -16=0 F
∏¿´ƒ√P¿g¿t™¿£¿ƒþ ©r∏¿ƒ™¡.
![]() Ý3x2
=16 (16 £¿þ ßÆ®s¡U¿P…Ã
v¿A¢z…, Cx¿™¡ Jg¿q¿∆ P¿q… 16 £¿ƒþ P¿∆rπz…)
Ý3x2
=16 (16 £¿þ ßÆ®s¡U¿P…Ã
v¿A¢z…, Cx¿™¡ Jg¿q¿∆ P¿q… 16 £¿ƒþ P¿∆rπz…)
x2 =16/3
![]() x =
x = ![]()
![]() =
= ![]() ÝÝÝÝ
ÝÝÝÝ![]() /
/![]() =
= ![]() ÝÝÝ(4/
ÝÝÝ(4/![]() )
)
2.19 ∏¿™¿ƒ∏…Â1:Ý
©rπ: x2/2 ñ 3/4 = 29/4
•¿j∫¡g¿:
•¿P¡ÎAv¿g¿ ™¿i¡rz¡U¿,
x2/2 = 29/4+3/4 = (29+3)/4 = 32/4 =8
![]() Ýx2
=16
Ýx2
=16
![]() x =
x = ![]() 4
4
2.19 ∏¿™¿ƒ∏… 2 : ©rπ: (2m-5)2=
81
•¿j∫¡g¿:
Ý(2m-5)2= 92
![]() Ý2m-5 =
Ý2m-5 = ![]() 9
9
![]() Ý2m =
Ý2m = ![]() 9 +5 (•¿P¡ÎAv¿g¿ ™¿i¡rz¡U¿)
9 +5 (•¿P¡ÎAv¿g¿ ™¿i¡rz¡U¿)
![]() Ý2m = +9+5 =14 Cx¿™¡ 2m =
-9+5 = -4
Ý2m = +9+5 =14 Cx¿™¡ 2m =
-9+5 = -4
![]() m= 7 Cx¿™¡ m= -2
m= 7 Cx¿™¡ m= -2
v¡º…:
m =ÝÝ 7: Dz¡U¿, (2m-5)2=(9)2=81= ßÆߢ.
m = - 2:Ý Dz¡U¿, (2m-5)2=(-4-5)2=(-4-5)2=(-9)2=81= ßÆߢ.
2.19 ∏¿™¿ƒ∏… 3 :Ý c2= a2+b2
DVz¿ƒðÝ a=8, c=17 Dz¡U¿ bAi¿ƒ ®…Ø… K£¿ƒ?
•¿j∫¡g¿:
c2= a2+b2
![]() Ýb2=
c2-a2
Ýb2=
c2-a2
![]() Ýb =
Ýb = ![]()
![]() (c2-a2)Ý (
(c2-a2)Ý (![]() DAz¿g… ™¿U¿™¿ƒ∆Æ)
DAz¿g… ™¿U¿™¿ƒ∆Æ)
a ™¿ƒv¿ƒ€ c U¿º¿
®…Ø…U¿º¿£¿ƒþ E∞Ë Dz…√≤πz¡U¿,
b = ![]()
![]() (c2-a2)
(c2-a2)
ÝÝ = ![]()
![]() (172-82)
(172-82)
ÝÝ = ![]()
![]() (289-64)
=
(289-64)
= ![]()
![]() (225)
=
(225)
= ![]() 15
15
v¡º…:
a=8, b=15 Dz¡U¿ ßÆߢ= a2+b2=64+225
=289 = 172= c2=Jq¿ß¢
2.19 ∏¿™¿ƒ∏… 4 : MAz¿ƒ π∞Aq¿j£¿ wÊd ërí Jv¿€g¿ íhíÝ Dz¡U¿ Cz¿g¿ W¿£¿•s¿Æ(U¡v¿Ê) = V = ![]() r2hÝ
r2hÝ
1. r£¿Ý ∏¿∆v¿Ê K£¿ƒ?
2. U¡v¿Ê=176 , Jv¿€g¿=14Dz¡U¿ π∞Aq¿j£¿ wÊd P¿Aq¿ƒªr.
•¿j∫¡g¿:
V =![]() r2hÝ
r2hÝ
r2= V/![]() h
h
![]() Ýr =
Ýr = ![]()
![]() (V/
(V/![]() h)
h)
z¿v¡€A±¿: V=176, h = 14Ý
![]() Ý= 22/7 (∏¿´ƒ√•¿z¿ ®…Ø…)
Ý= 22/7 (∏¿´ƒ√•¿z¿ ®…Ø…)
Ý r2=V/![]() h =
176*7/(22*14)= 4
h =
176*7/(22*14)= 4
![]() Ýr =
Ýr = ![]() 2
2
wÊd™¿≈ Iƒt ∏¿AS…ÂAi¿i¡U¿ƒ™¿≈¢ÆË. Dz¿ðjAz¿ r=2 ™¿i¡£¿U¿º¿ƒ.
v¡º…:
![]() Ý= 22/7, h =14,
r=2:Ý
Ý= 22/7, h =14,
r=2:Ý
ßÆ®s¡U¿= ![]() r2h= 22*4*14/7 = 22*4*2=176=V= Jq¿®s¡U¿
r2h= 22*4*14/7 = 22*4*2=176=V= Jq¿®s¡U¿
2.19.1 ´ƒ±¿Ê
™¿U¿ ∏¿´ƒ√P¿g¿t™¿£¿ƒþ C•¿™¿v¿£¿ P¿Ê™¿ƒ¢Az¿ ©r∏¿ƒ™¿≈z¿ƒ(Solving
Adfected Quadratic equations by Factorisation method)
F ´zs¡£¿z¿∞Ë £¡™¿≈ ™¿U¿ ∏¿´ƒ√P¿g¿t™¿£¿ƒþ Jg¿q¿ƒ ¢È•¿z¿U¿º¿ U¿ƒtÆßÞ™¡V
ßg…z¿ƒ, •¿ÊwAi…∆Az¿£¿ƒþ ∏…∆£…þU… ∫…∆√∞π, Z¿g¡P¿Îg¿z¿ ®…Ø…Ai¿ƒ£¿ƒþ
P¿Aq¿ƒªrAi¿ƒƒv…€√™…. F ´zs¡£¿P…à v¿ƒA®¡ C®s¡Â∏¿®…√P¿ƒ ™¿ƒv¿ƒ€ ∏¿jAi¿i¡VÝ P¿∞Ai¿ƒÆƒ v¿ƒA®¡ ∏¿™¿ƒAi¿ƒ®…√P¿ƒ.
2.19.1 ∏¿™¿ƒ∏… 1: ©rπ: Ý6-p2=p
•¿j∫¡g¿:
•¿P¡ÎAv¿g¿ ™¿i¡rz¡U¿, z¿v¿€ ∏¿™¿ƒ∏…Â: p2+p-6 = 0
FU¿, Jq¿®s¡U¿™¿£¿ƒþ (x+a)(x+b)
g¿∆•¿z¿∞Ë ßg…Ai¿ƒ®…√P¿ƒ.
E∞Ë a+b =1, ab = -6.Ý
- 6 g¿
C•¿™¿v¿£¿U¿º¿ Ai¿ƒƒU¿‰U¿º¿ƒ (1,
-6), (-1,6), (2,-3), (-2,3), (3,-2), (-3,2)
E™¿≈U¿º¿∞Ë a+b =1, ab =
-6.Ý F §Ai¿ƒ™¿ƒP…à C£¿ƒ∏¡g¿™¡Vg¿ƒ™¿ U¿ƒA•¿≈
a = -2 and b= 3Ý
![]() p2+p-6 = p2+3p-2p -6
p2+p-6 = p2+3p-2p -6
= p(p+3) -2(p+3)Ý ---- ∏¡™¿i¡£¿Â •¿z¿(p+3)™¿£¿ƒþ ∫…∆g¿
v…U…z¡U¿
= (p+3)(p-2)
p2+p-6 = 0
(p+3)(p-2) = 0 (Jg¿q¿ƒ •¿z¿U¿º¿
U¿ƒtÆßÞ 0 Dz¿g… C™¿≈U¿º¿∞Ë MAz¿ƒ •¿z¿ 0
DVg¿Ø…√®…√P¿ƒ.)
p+3 = 0 Cx¿™¡ p-2 = 0
![]() Ýp= -3 Cx¿™¡
p =2 E™¿≈
∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿ƒ.
Ýp= -3 Cx¿™¡
p =2 E™¿≈
∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿ƒ.
v¡º…:
p=2 Dz¡U¿,
Jq¿®s¡U¿: 22+2-6 =4+2-6 = 0 = ßÆ®s¡U¿.
p = -3 Dz¡U¿, Jq¿®s¡U¿: (-3)2Ý -3- 6 = 9-3-6
= 0 ßÆ®s¡U¿.
2.19.1 ∏¿™¿ƒ∏… 2: ©rπ: 6y2+y
-15 = 0.
•¿j∫¡g¿:
FU¿ Jq¿ß¢Ai¿ƒ£¿ƒþ £¡™¿≈ (ax+b)(cx+d)={
acx2 + x(ad+bc)+bd} g¿∆•¿P…Ã
•¿j™¿w∏¿®…√P¿ƒ.
E∞Ë ac=6, bd= -15,Ý ad+bc =1 DVg¿®…√P¿ƒ.
•¿j≤√Æ£…¨ƒAz¿ a=3, c=2, b=5,
d= -3 DVg¿ƒv¿€z….
![]() 6y2+y -15
6y2+y -15
= 6y2+10y -9y -15
= 2y(3y+5)-3(3y+5) ñ ∏¡™¿i¡£¿Â
•¿z¿3y+5 ™¿£¿ƒþ ∫…∆g¿ v…U…z¡U¿
= (3y+5)(2y-3)
Ý6 y2+y -15 =0 DVg¿ƒ™¿≈z¿jAz¿
(3y+5)(2y-3) =0
Ý3y+5 = 0 Cx¿™¡ 2y-3
=0
![]() Ýy = -5/3 Cx¿™¡ y
=3/2E™¿≈ ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿ƒ.
Ýy = -5/3 Cx¿™¡ y
=3/2E™¿≈ ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿ƒ.
v¡º…:
y=3/2 Dz¡U¿,
Jq¿ß¢ = 6*9/4 +3/2 -15
Ý=27/2+3/2 -15
Ý= (27+3)/2 ñ 15
= 0 = ßÆߢ
Ez…√j√w y= -5/3 Dz¡U¿ v¡º…£…∆√r.
2.19.1 ∏¿™¿ƒ∏… 3: ©rπ: Ý13m = 6(m2+1)
•¿j∫¡g¿:
6m2-13m+6 =0
FU¿ Jq¿®s¡U¿™¿£¿ƒþ
(ax+b)(cx+d)={ acx2 + x(ad+bc)+bd} g¿∆•¿P…à v¿g¿®…√P¿ƒ.
E∞Ë ac=6, bd= 6, ad+bc = -13 DVg¿®…√P¿ƒ.
•¿j≤√Æ£…¨ƒAz¿ a=3, c=2,b=5,d=
-3
i.e 6m2-13m+6=0
= 6m2-9m -4m+6
= 3m(2m -3) -2(2m-3)Ý ------ý ∏∏¡™¿i¡£¿Â
•¿z¿2m-3™¿£¿ƒþ ∫…∆g¿v…U…z¡U¿
Ý= (2m-3)(3m-2)
![]() Ý 6m2-13m+6
=0
Ý 6m2-13m+6
=0
(2m-3)(3m-2)=0
![]() Ý2m-3 = 0Ý Cx¿™¡ÝÝ 3m-2 =0
Ý2m-3 = 0Ý Cx¿™¡ÝÝ 3m-2 =0
![]() Ým = 3/2 Cx¿™¡ m
=2/3 E™¿≈ z¿v¿€ ∏¿´ƒ√P¿g¿tz¿
™¿ƒ∆ÆU¿º¿ƒ.
Ým = 3/2 Cx¿™¡ m
=2/3 E™¿≈ z¿v¿€ ∏¿´ƒ√P¿g¿tz¿
™¿ƒ∆ÆU¿º¿ƒ.
v¡º…:
m=2/3 Dz¡U¿,
Jq¿®s¡U¿ = 6*4/9 -13*2/3 +6
ÝÝÝÝ = 8/3
-26/3+6
ÝÝÝÝ =(8-26)/3
+6 = 0 =ßÆ®s¡U¿.
m= 3/2 Dz¡U¿ v¡º… £…∆√r.
™…ƒ√∞ ´™¿jπz¿Av¿∫¿ ´zs¡£¿P…à v¿ƒA®¡ C®s¡Â∏¿ ∫¡U¿∆
∏¿™¿ƒAi¿ƒ™¿«®…√P¿ƒ.ª√Vg¿ƒ™¡U¿ KP… ∏¿∆v¿Ê™…«Az¿£¿ƒþ P¿Aq¿ƒªrAi¿ƒ®¡g¿z¿ƒ?
2.19.1 ∏¿™¿ƒ∏… 4:ÝÝ 2x2+3x+1
=0 ÝJ£¿ƒþ™¿≈z¿£¿ƒþ ©r∏¿ƒ™¡.
|
CA. |
∫¿Av¿ |
´™¿g¿u… |
|
1 |
x2
+(3/2)x+ (1/2) =0Ý |
Jg¿q¿∆
ߢU¿º¿£¿ƒþ 2 jAz¿ ®s¡Vπz…. |
|
2 |
x2+(3/2)x=
-(1/2) |
(1/2)Ý £¿ƒþ ßÆߢU… v¿A¢z…. |
|
(x+a)2
= x2+2ax+ a2 J£¿ƒþ™¿ ∏¿∆v¿Ê™¿£¿ƒþ G•¿Ai…∆√V∏¿ƒ™¿ ∫¡Vz¿ð∞Ë ™¿ƒ∆Æ™¿£¿ƒþ
P¿Aq¿ƒªrAi¿ƒß∫¿ƒz¿ƒ. ª√Vg¿ƒ™¡U¿ 2ax = (3/2)xÝ JAz¿ƒ wΩAi¿ƒß∫¿ƒz¿ƒ. Ý |
||
|
3 |
x2+(3/2)x+ (3/4)2 = -(1/2)+
(3/4)2ÝÝÝÝÝÝÝ |
Ý(3/4)2 £¿ƒþ Jg¿q¿∆ ߢU¿ΩU… P¿∆rπz…. |
|
4 |
ÝLHSÝ =
x2 +2(3/4)x +
(3/4)2= [x+(3/4)]2 |
p2+2pq+q2
= (p+q)2 E∞Ë Ýp=x, q= 3/4 |
|
5 |
RHSÝ = -(1/2)+ (3/4)2 =-(1/2)+ (9/16)= (1/16) |
∏¡™¿i¡£¿Â
b…√z¿ 4*4=16 |
|
6 |
[x+(3/4)]2=(1/16) |
∫¿Av¿ 4™¿ƒv¿ƒ€
5jAz¿ LHS=RHS |
|
7 |
(x+(3/4)) = |
∫¿Av¿ 6Ý g¿ ™¿U¿™¿ƒ∆Æ |
|
8 |
x = -(3/4) |
3/4Ý £¿ƒþ ™¿U¡Av¿jπ |
™…ƒ√∞ ´™¿jπz¿Av¿∫¿ ´zs¡£¿z¿Av… ax2 +bx+ c =0 z¿ ™¿ƒ∆Æ P¿Aq¿ƒªrAi¿ƒƒ™¡.
™¿U¿∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿£¿ƒþ P¿Aq¿ƒªrAi¿ƒƒ™¿
∏¿∆v¿Ê(Formula for
finding roots of the quadratic equation)
™¿U¿ ∏¿´ƒ√P¿g¿tz¿ ∏¡™¿i¡£¿Â g¿∆•¿: ax2 +bx+ c =0,E∞Ë a, b, c
U¿º¿ƒ ™¡∏¿€´P¿ ∏¿AS…ÂU¿º¡Vz¿ƒð a ![]() 0, b
0, b ![]() 0. F ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿£¿ƒþ P¿Aq¿ƒªrAi¿ƒƒ™¡.
0. F ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿£¿ƒþ P¿Aq¿ƒªrAi¿ƒƒ™¡.
|
CA. |
∫¿Av¿ |
´™¿g¿u… |
|
1 |
x2
+(bx/a)+ (c/a) =0Ý |
Jg¿q¿∆
ߢU¿º¿£¿ƒþ ëaí¨ƒAz¿ ®s¡Vπz…. |
|
2 |
x2
+(bx/a) = -( c/a) |
c/aÝ Ai¿ƒ£¿ƒþ ßÆߢU… v¿A¢z…. |
|
3 |
x2 +(bx/a) + (b/2a)2 = -( c/a) + (b/2a)2ÝÝÝÝÝÝ |
Ý(b/2a)2 ™¿£¿ƒþ Jg¿q¿∆ ߢU¿ΩU… P¿∆rπz…. |
|
4 |
LHS= x2 +(bx/a) + (b/2a)2=
[x+(b/2a)]2 |
p2+2pq+q2
= (p+q)2 E∞Ë Ýp=x, q= b/2a |
|
5 |
RHS = b2/4a2- c/a=
(b2-4ac)/ 4a2 |
∏¡™¿i¡£¿Â
b…√z¿ 4a2 |
|
6 |
[x+(b/2a)]2
=(b2-4ac)/ 4a2 |
∫¿Av¿ 4™¿ƒv¿ƒ€
5jAz¿ LHS=RHS |
|
7 |
x+(b/2a) = = |
∫¿Av¿ 6Ý g¿ ™¿U¿™¿ƒ∆Æ |
|
8 |
x = [-b |
b/2a £¿ƒþ RHS U… •¿P¡ÎAv¿jπ. |
ax2 +bx+ c =0Ý ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿ƒ:
x = [-b +![]() (b2-4ac)]/2aÝ ™¿ƒv¿ƒ€ ÝÝx = [-b -
(b2-4ac)]/2aÝ ™¿ƒv¿ƒ€ ÝÝx = [-b -![]() (b2-4ac)]/2aÝÝÝ
(b2-4ac)]/2aÝÝÝ
U¿™¿ƒ§π:
F ∏¿∆v¿Ê™¿£¿ƒþ ™¿U¿∏¿∆v¿Ê J£¿ƒþ™¿g¿ƒ ™¿ƒv¿ƒ€ Ez¿£¿ƒþ
•¿Ê•¿Êx¿™¿ƒ™¡V ®s¡g¿w√Ai¿ƒ U¿t¬v¿d’ ≤Ê√zs¿g¡Z¡Ai¿ƒ g¿ƒ(1025AD) •¿jZ¿¨ƒπg¿ƒv¡€g…. Ez¿£¿ƒþ ±…∆Ë√P¿g¿∆•¿z¿∞Ë ∞√Ø¡™¿wAi¿ƒÆ∆Ë
P…∆n÷z…(±…∆Ë√P¿ 67)
2.19.1 ∏¿™¿ƒ∏… 5: ©rπ: 4x2+8x+4 = 0
•¿j∫¡g¿:
E∞Ë FU¿, a =4, b=8, c =4
![]() Ýb2-4ac = 64 ñ 4*4*4 = 0
Ýb2-4ac = 64 ñ 4*4*4 = 0
![]() Ý
Ý![]() (b2-4ac) =
(b2-4ac) = ![]() (0)
= 0
(0)
= 0
™¿ƒ∆ÆU¿º¿ƒ: p = [-b +![]() ]/2aÝ =(-8+0)/8Ý
= - 1ÝÝÝ
Cx¿™¡
]/2aÝ =(-8+0)/8Ý
= - 1ÝÝÝ
Cx¿™¡
ÝÝÝÝÝÝÝ p = [-b -![]() ]/2aÝÝ = (-8-0)/8 =Ý
- 1
]/2aÝÝ = (-8-0)/8 =Ý
- 1
E∞Ë ™¿ƒ∆ÆU¿º¿ƒ ∏¿™¿ƒ™¡V™…: - 1
U¿™¿ƒ§π: Ý4x2+8x+4 = 4(x2+2x+1)
= 4(x+1)(x+1). F •¿ÊP¡g¿™¿« x=-1 ™¿ƒ∆Æ™…√ DVz….
2.19.1 ∏¿™¿ƒ∏… 6:Ý
©rπ:ÝÝ p2+p-6
= 0(2.19.1.1 g¿∞Ë ™¿i¡rz¿
Ø…P¿Ã™…√ Ez¡Vz….)
•¿j∫¡g¿:
∏¿´ƒ√P¿g¿t™¿≈ ax2 +bx+ c =0 g¿∆•¿z¿∞Ëz….
a =1, b=1, c =-6
![]() Ýb2-4ac = 1 ñ 4*1*(-6) = 25
Ýb2-4ac = 1 ñ 4*1*(-6) = 25
![]() Ý
Ý![]() Ý=
Ý= ![]() (25)
=
(25)
= ![]() 5
5
∏¿∆v¿Êz¿Av…:
p = [-b +![]() ]/2aÝ =(-1+5)/2Ý
= 2Ý Cx¿™¡
]/2aÝ =(-1+5)/2Ý
= 2Ý Cx¿™¡
p = [-b -![]() ]/2aÝÝ = (-1-5)/2 =Ý
-3
]/2aÝÝ = (-1-5)/2 =Ý
-3
F ™¿ƒ∆ÆU¿º¿ƒ F ªAz…Ai…ƒ√ z…∆g…w™… (2.19.1.1)
2.19.1 ∏¿™¿ƒ∏… 7: ©rπ: 6y2+y
-15 = 0 (2.19.1.2g¿∞Ë ™¿i¡rz…)
•¿j∫¡g¿:
∏¿´ƒ√P¿g¿t™¿≈ ax2 +bx+ c =0
g¿∆•¿z¿∞Ëz….
a=6, b=1, c= -15
![]() Ýb2-4ac = 1 ñ 4*6*(-15) = 361
Ýb2-4ac = 1 ñ 4*6*(-15) = 361
![]() Ý
Ý![]() (b2-4ac) =
(b2-4ac) = ![]() (361)
=
(361)
= ![]() 19
19
∏¿∆v¿Êz¿Av…,
y = [-b +![]() ]/2aÝ =(-1+19)/12Ý
= 18/12= 3/2ÝÝÝÝÝ Cx¿™¡
]/2aÝ =(-1+19)/12Ý
= 18/12= 3/2ÝÝÝÝÝ Cx¿™¡
y = [-b -![]() ]/2aÝÝ = (-1-19)/12 =Ý -20/12 = -5/3
]/2aÝÝ = (-1-19)/12 =Ý -20/12 = -5/3
F ™¿ƒ∆ÆU¿º¿£¿ƒþ £¡™¿≈ F ªAz…Ai…ƒ√ •¿q…¢z…ð√™….
Ý3/2 ™¿ƒv¿ƒ€Ý -5/3ÝÝ ™¿ƒ∆ÆU¿º¿ƒ DVg¿ƒ™¿≈z¿jAz¿ (y-3/2)(y+5/3)Ý C•¿™¿v¿£¿U¿º¿ƒ DV™….
Ý(y-3/2)(y+5/3) = (2y-3)(3y+5)/6
![]() 6y2+y -15 = (2y-3)(3y+5)
6y2+y -15 = (2y-3)(3y+5)
Z¿lƒ™¿nP…: 2.19.1.3 g¿∞Ë P…∆l÷ ∏¿™¿ƒ∏…ÂAi¿ƒ£¿ƒþ ∏¿∆v¿Ê G•¿Ai…∆√Vπ ©rπ.
2.19.1 ∏¿™¿ƒ∏… 8: ©rπ: Ýy2-2y+2
=0
•¿j∫¡g¿:
z¿v¿€ ∏¿´ƒ√P¿g¿t™¿≈ ax2 +bx+ c =0 g¿∆•¿z¿∞Ëz….
a=1, b=-2, c=2
![]() Ýb2-4ac = 4 ñ 4*1*2 = -4
Ýb2-4ac = 4 ñ 4*1*2 = -4
![]() Ý
Ý![]() (b2-4ac) =
(b2-4ac) = ![]() (-4)
= 2
(-4)
= 2![]()
∏¿∆v¿Êz¿Av…,
y = [-b +![]() ]/2aÝ =(2+2
]/2aÝ =(2+2![]() )/2Ý =Ý 1+
)/2Ý =Ý 1+![]() Cx¿™¡
Cx¿™¡
y = [-b -![]() ]/2aÝÝ = (2-2
]/2aÝÝ = (2-2![]() )/2
=Ý 1-
)/2
=Ý 1-![]()
™¿ƒ∆ÆU¿º¿ƒ ™¡∏¿€™¿ ∏¿AS…ÂU¿º¿ÆË.
v¡º…:
z¿v¿€ ∏¿´ƒ√P¿g¿tz¿∞Ë y= 1+![]() £¿þ Dz…√≤π,
£¿þ Dz…√≤π,
y2-2y+2 = (1+![]() )2
-2(1+
)2
-2(1+![]() ) +2 ((1+
) +2 ((1+![]() )2 (´∏¿€j∏¿Æƒ (a+b)2 =a2+b2+2ab ∏¿∆v¿ÊÝ
G•¿Ai…∆√Vπ)
)2 (´∏¿€j∏¿Æƒ (a+b)2 =a2+b2+2ab ∏¿∆v¿ÊÝ
G•¿Ai…∆√Vπ)
= [1 +(-1) +2![]() ] +[-2 -2
] +[-2 -2![]() ] +2
] +2
=Ý 1-1 +2![]() -2 -2
-2 -2![]() +2 = 0 = ßÆߢ.
+2 = 0 = ßÆߢ.
Ez…√ j√w E£…∆þAz¿ƒ ™¿ƒ∆Æ = 1-![]() P¿∆à v¡º…£…∆√r.
P¿∆à v¡º…£…∆√r.
2.19.1 ∏¿™¿ƒ∏… 9: ©rπ: Ý2(3y-1)/(4y-3)
= 5y/(y+2) -2
•¿j∫¡g¿:
ßÆߢ= [5y -2(y+2)]/(y+2) = (3y-4)/(y+2)
![]() ÝFU¿ £¡™¿≈ ©r∏¿®…√P¡z¿z¿ƒð: 2(3y-1)/(4y-3) = (3y-4)/(y+2)
ÝFU¿ £¡™¿≈ ©r∏¿®…√P¡z¿z¿ƒð: 2(3y-1)/(4y-3) = (3y-4)/(y+2)
Cq¿ÿ U¿ƒu¡P¡g¿¢Az¿, 2(3y-1)*(y+2)
= (3y-4)*(4y-3)
![]() Ý2(3y2+6y
ñy -2) = 12y2-9y -16y+12
Ý2(3y2+6y
ñy -2) = 12y2-9y -16y+12
![]() Ý6y2+10y -4 = 12y2-25y +12(•¿P¡ÎAv¿jπz¡U¿)
Ý6y2+10y -4 = 12y2-25y +12(•¿P¡ÎAv¿jπz¡U¿)
6y2-35y +16=0
FU¿ F ∏¿´ƒ√P¿g¿t™¿≈ ax2
+bx+ c =0 g¿∆•¿z¿∞Ëz….
E∞Ë a=6, b=-35, c= 16
![]() Ýb2-4ac = 1225Ý ñ 4*6*16
= 1225-384Ý = 841
Ýb2-4ac = 1225Ý ñ 4*6*16
= 1225-384Ý = 841
![]() Ý
Ý![]() (b2-4ac) =
(b2-4ac) = ![]() (841)
= 29
(841)
= 29
∏¿∆v¿Êz¿Av…,
y = [-b +![]() ]/2aÝ =(35+29)/12Ý
=Ý 16/3 Cx¿™¡
]/2aÝ =(35+29)/12Ý
=Ý 16/3 Cx¿™¡
y = [-b -![]() ]/2aÝÝ = (35-29)/12 =Ý 1/2
]/2aÝÝ = (35-29)/12 =Ý 1/2
v¡º…
z¿v¿€ ∏¿´ƒ√P¿g¿tz¿∞Ë F ®…Ø…U¿º¿£¿ƒþ ∫¡Q v¡º… £…∆√r.
2.19.1 ∏¿™¿ƒ∏… 10: ©rπ: (y-1)(5y+6) /(y-3) = (y-4)(5y+6)/(y-2)
•¿j∫¡g¿:
∏¿´ƒ√P¿g¿tz¿∞Ë Cq¿ÿ U¿ƒu¡P¡g¿ ™¿i¡rz¡U¿,
(y-1)(5y+6)(y-2) = (y-4)(5y+6)(y-3)
Jq¿®s¡U¿ = (5 y2+6y-5y-6)(y-2)
= (5 y2+y-6)(y-2)
= 5 y3+ y2-6y -10 y2-2y+12
=5 y3 -9y2-8y+12
ßÆ®s¡U¿ =Ý (5y2+6y-20y-24)(y-3)
= (5y2-14y -24)(y-3)
= 5y3-14 y2-24yÝ
-15y2+42y+72
= 5y3-29y2+18y+72
Jq¿®s¡U¿ = ßÆ®s¡U¿
5 y3 -9y2-8y+12= 5y3-29y2+18y+72.
(•¿P¡ÎAv¿jπz¡U¿)
5 y3 -9y2-8y+12-(5y3-29y2+18y+72)
=0
20y2-26y-60 = 0 ( 2 £¿ƒþ ∫…∆g¿v…U¿z¡U¿)
10y2-13y-30 = 0
FU¿ ∏¿´ƒ√P¿g¿t: ax2
+bx+ c =0 g¿∆•¿z¿∞Ëz….
a=10, b=-13, c= -30
![]() Ýb2-4ac = 169Ý ñ
4*10*(-30) = 169+1200Ý = 1369
Ýb2-4ac = 169Ý ñ
4*10*(-30) = 169+1200Ý = 1369
![]() Ý
Ý![]() (b2-4ac) =
(b2-4ac) = ![]() (1369)
= 37
(1369)
= 37
∏¿∆v¿Êz¿Av…,
y = [-b +![]() ]/2aÝ =(13+37)/20Ý
=Ý 50/20 = 5/2 Cx¿™¡
]/2aÝ =(13+37)/20Ý
=Ý 50/20 = 5/2 Cx¿™¡
y = [-b -![]() ]/2aÝÝ = (13-37)/20 = -24/20 =Ý -6/5
]/2aÝÝ = (13-37)/20 = -24/20 =Ý -6/5
v¡º…:
yAi¿ƒ
®…Ø…Ai¿ƒ£¿ƒþ ∏¿´ƒ√P¿g¿tz¿∞Ë Dz…√≤π LHS = RHS ßg¿ƒv¿€z….
™…ƒ√∞£¿ ∏¿™¿ƒ∏…ÂAi¿ƒ£¿ƒþ ©r∏¿ƒ™¿ •¿Ai¿i¡Ai¿ƒ ´zs¡£¿:-
z¿v¿€ ∏¿´ƒ√P¿g¿tz¿∞Ë (5y+6) ∏¡™¿i¡£¿Â C•¿™¿v¿£¿, £¿™¿ƒV√U¿ 2 DAi…ƒÃU¿Ω™…:-
CAz¿g…
(1) 5y+6 = 0:
DU¿ 5y= -6ÝÝ y = -6/5
![]() Ý y = -6/5 JA߃z¿ƒ z¿v¿€
∏¿™¿ƒ∏…ÂAi¿ƒ •¿j∫¡g¿ ---------ý(1)
Ý y = -6/5 JA߃z¿ƒ z¿v¿€
∏¿™¿ƒ∏…ÂAi¿ƒ •¿j∫¡g¿ ---------ý(1)
(2) 5y+6 ![]() Ý0 Dz¿g…, 5y+6 jAz¿ Jg¿q¿∆ ߢU¿º¿£¿ƒþ ®s¡Vπ,
Ý0 Dz¿g…, 5y+6 jAz¿ Jg¿q¿∆ ߢU¿º¿£¿ƒþ ®s¡Vπ,
[(y-1)/(y-3)] =[(y-4)/(y-2)] :
Cq¿ÿ U¿ƒu¡P¡g¿ ™¿i¡r,
ÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝ (y-1)(y-2) =
(y-4)(y-3)
CAz¿g… Ýy2-2y-y+2 = y2-3y-4y+12
CAz¿g… Ýy2-3y+2 = y2-7y+12: (•¿P¡ÎAv¿jπz¡U¿)
CAz¿g… y2-3y+2-(
y2-7y+12)=0
CAz¿g…Ý y2-3y+2-y2+7y-12=0
CAz¿g…Ý 4y-10=0
CAz¿g… 4y=10 or
y=10/4 =5/2Ý
---------------------------ý(2)
(1) ™¿ƒv¿ƒ€ (2) jAz¿,
z¿v¿€ ∏¿´ƒ√P¿g¿tz¿ ™¿iÀÆÂU¿º¿ƒ: 5/2 ™¿ƒv¿ƒ€ -6/5
2.19.1 ∏¿™¿ƒ∏… 11: y/(y+1) + (y+1)/y = 25/12
•¿j∫¡g¿:
z¿v¿€ ∏¿´ƒ√P¿g¿tz¿ Jq¿ß¢Ai¿ƒ£¿ƒþ ∏¿ƒÆ©¸√P¿jπz¡U¿,
[y*y +(y+1)(y+1)]/[y(y+1)]
= (y2+y2+2y+1)/( y2+y)
ÝLHS = RHS DVg¿ƒ™¿≈z¿jAz¿
(y2+y2+2y+1)/( y2+y) = 25/12
Cq¿ÿ U¿ƒu¡P¡g¿ ™¿i¡r,
12(y2+y2+2y+1) = 25( y2+y)
![]() Ý24y2+24y+12 = 25y2+25y.
Ý24y2+24y+12 = 25y2+25y.
Jq¿ß¢Ai¿ƒ∞Ëg¿ƒ™¿≈z¿£¿ƒþ ßÆߢU… P…∆Aq¿ƒ∫…∆√V.
0 = y2+y-12
F ∏¿´ƒ√P¿g¿t™¿≈ ax2 +bx+ c =0 g¿∆•¿z¿∞Ëz….
a=1, b=1, c=
-12
![]() Ýb2-4ac = 1Ý
ñ 4*1*(-12) = 1+48 = 49
Ýb2-4ac = 1Ý
ñ 4*1*(-12) = 1+48 = 49
![]() Ý
Ý![]() Ý=
Ý= ![]() (49)
=
(49)
= ![]() 7
7
∏¿∆v¿Êz¿Av…,
™¿ƒ∆ÆU¿º¿ƒ:
y = [-b +![]() )]/2aÝ =(-1+7)/2Ý
=Ý 3
Cx¿™¡
)]/2aÝ =(-1+7)/2Ý
=Ý 3
Cx¿™¡
y = [-b -![]() )]/2aÝÝ = (-1-7)/2 =Ý
- 4
)]/2aÝÝ = (-1-7)/2 =Ý
- 4
v¡º…:
F ®…Ø…U¿º¿£¿ƒþ z¿v¿€ ∏¿´ƒ√P¿g¿tz¿∞Ë Dz…√≤πz¡U¿
Jq¿ß¢=ßÆߢ ßg¿ƒv¿€z….
2.19.1 ∏¿™¿ƒ∏… 12 : ©rπ: (3x2-5x+2)
(3x2-5x-2)=21
•¿j∫¡g¿:
1.Ý 3x2-5x = y DVg¿∞, DU¿ z¿v¿€ ∏¿´ƒ√P¿g¿t: (y+2) (y-2) =21
y2 ñ 4 = 21
y2 = 21+4 =25
y =![]()
![]() (25)=
(25)= ![]() 5
5
2. ![]() Ýy = 3x2-5x =
Ýy = 3x2-5x =![]() 5
5
![]() 3x2-5x
3x2-5x ![]() Ý5=0
Ý5=0
x = - (-5) ![]() Ý
Ý![]() (25+60)/2*3
= 5
(25+60)/2*3
= 5 ![]() Ý
Ý![]() (85)/6
(85)/6
2.19.1 ∏¿™¿ƒ∏… 13 (F ´®s¡U¿z¿ Dg¿A®s¿z¿∞Ë P…∆l÷ ∏¿AS…Â): §√™¿≈ §™¿ƒ‰ ∏…þ√ªv¿g…∆q¿U¿∆r MAz¿ƒ •¿Ê™¡∏¿P…à ∫…∆√U¿Æƒ
§zs¿j∏¿ƒw€√j. D∫¡g¿P¡ÃV Mlƒ÷ 480g¿∆. RZ¡U¿ƒv¿€z…. Dz¿g… P…∆£… P¿Îtz¿∞Ë §™¿ƒ‰ 8 d£¿
∏…þ√ªv¿g¿ƒ •¿Ê™¡∏¿P…à ßg¿∞ÆË. ∫¡U¡V •¿ÊwAi…∆ß‚g¿∆ D∫¡g¿P¡ÃV 10g¿∆.
∫…a—U… P…∆q¿®…√P¡¨ƒv¿ƒ. ∫¡U¡z¿g… P…∆£…Ai¿ƒ∞Ë •¿ÊwAi…∆ß‚g¿∆ P…∆l÷ ∫¿t Jµ¿ƒ÷?
•¿j∫¡g¿:
•¿Ê™¡∏¿P…à ∫…∆√U¿Æƒ ™…∆z¿Æƒ §zs¿jπz¿™¿g¿ ∏¿AS…Â:
Ýëxí
DU¿ D∫¡g¿P¡ÃV •¿ÊwAi…∆ß‚jU… v¿U¿Æƒ™¿ ™…Z¿—: 480/x
8 d£¿
®¡g¿¢z¿ƒðz¿jAz¿ •¿Ê™¡∏¿P…à ∫…∆√z¿™¿g¿ ∏¿AS…Â: (x-8)
FU¿ •¿ÊwAi…∆ß‚jU… v¿U¿Æƒ™¿ ™…Z¿— = 480/(x-8)
F ∫¿t™¿≈ ™¿ƒƒAZ… §zs¿jπz¿ ∫¿tP¡ÃV 10g¿∆.
∫…Z¿ƒ—
![]() ∫…∆∏¿z¿g¿= ∫¿º…z¿g¿ +10
∫…∆∏¿z¿g¿= ∫¿º…z¿g¿ +10
480/(x-8) = 480/x + 10Ý
480/(x-8) = (480+10x)/x.
Cq¿ÿ U¿ƒu¡P¡g¿ ™¿i¡r,
480x = (480+10x)(x-8)
RHS= 480x -480*8 +10x*x-80x
Ý= 480x -Ý 3840+ 10x2-80x
= 10x2+400x-3840
![]() 0 =10x2+400x-3840-480x. (•¿P¡ÎAv¿jπz¡U¿)
0 =10x2+400x-3840-480x. (•¿P¡ÎAv¿jπz¡U¿)
Cx¿™¡ 10x2-80x-3840
=0
F ∏¿´ƒ√P¿g¿t™¿£¿ƒþ 10 jAz¿ ®s¡Vπ.
x2-8x-384 =0
F ∏¿´ƒ√P¿g¿t™¿≈ ax2
+bx+ c =0 g¿∆•¿z¿∞Ëz….
a=10, b= -80, c= -3840
![]() Ýb2-4ac = 6400Ý ñ
4*10*(-3840) = 6400 +153600 =160000
Ýb2-4ac = 6400Ý ñ
4*10*(-3840) = 6400 +153600 =160000
![]() Ý
Ý![]() ÝÝ=
ÝÝ= ![]() (160000)
= 40
(160000)
= 40
∏¿∆v¿Êz¿Av… ™¿ƒ∆ÆU¿º¿ƒ:
x = [![]() ]
=(80+400)/20Ý =Ý 24 Cx¿™¡
]
=(80+400)/20Ý =Ý 24 Cx¿™¡
x = [-b -![]() ]/2aÝÝ = (80-400)/20 = -16
]/2aÝÝ = (80-400)/20 = -16
d£¿g¿ ∏¿AS…ÂAi¿ƒƒ Iƒt ∏¿AS…ÂAi¿i¡U¿ƒ™¿≈¢ÆË. Dz¿ðjAz¿ x = 24
24 d£¿g¿ƒ •¿Ê™¡∏¿
∫…∆√U¿Æƒ §zs¿jπz¿ðg¿ƒ.
P…∆£…Ai¿ƒ∞Ë •¿ÊwAi…∆ß‚g¿ƒ P…∆q¿®…√P¡z¿ ∫¿t (=![]() ) = 30g¿∆.
) = 30g¿∆.
v¡º…:
24 d£¿g¿ƒ
•¿Ê™¡∏¿P…à ∫…∆√U¿Æƒ §zs¿jπz¿ðg¿ƒ.
•¿ÊwAi…∆ß‚g¿ RZ¿ƒ = 480/24 = 20g¿∆.
8 d£¿
∫…∆√U¿¢z¿ƒðz¿jAz¿ •¿Ê™¡∏¿P…à ∫…∆√z¿™¿g¿ƒ = 24 - 8 = 16
FU¿ •¿ÊwAi…∆ß‚g¿ RZ¿ƒ = 480/16 = 30g¿∆.
Ez¿ƒ ™…∆z¿∞z¿QÃAv¿ 10g¿∆. ∫…Z¿ƒ.—
Gv¿€g¿ ∏¿™¿ƒ∏…ÂU… v¡º…Ai¿i¡U¿ƒv¿€z….
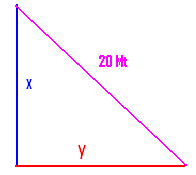
2.19.1 ∏¿™¿ƒ∏… 14:Ý MAz¿ƒ ÆAßP…∆√£¿ wÊP…∆√£¿z¿ ´P¿t 20´ƒ√lgÔ DVz….
GΩz…g¿q¿ƒ ®¡∫¿ƒU¿º¿ ™¿Âv¡Â∏¿ 4´ƒ√lgÔ Dz¿g…, D™…g¿q¿ƒ ®¡∫¿ƒU¿º¿ Gz¿ð P¿Aq¿ƒªr.
•¿j∫¡g¿:
|
ÆAßP…∆√£¿ wÊP…∆√£¿z¿∞Ë ´P¿t ©lƒ÷ GΩz…g¿q¿ƒ ®¡∫¿ƒU¿º¿ƒ x, y DVg¿∞. •… x¡U…∆g¿∏¿£¿ •¿Ê™…ƒ√Ai¿ƒz¿Av…, (´P¿t)2 = x2+ y2 . ´P¿t = 20´ƒ. ®¡∫¿ƒU¿º…g¿q¿g¿ ™¿Âv¡Â∏¿ 4´ƒÝ = x-y =
4:Ý x= 4+y. x£¿ F ®…Ø…Ai¿ƒ£¿ƒþ
∏¿´ƒ√P¿g¿t (1)g¿∞Ë Dz…√≤π, 400 = x2+ y2 =(4+y)2+ y2 =
(16+8y+ y2)+ y2 =16+8y+ 2y2. (•¿P¡ÎAv¿jπz¡U¿) 2y2+8y-384
= 0 F ∏¿´ƒ√P¿g¿t ax2 +bx+ c =0 g¿∆•¿z¿∞Ëz…. a=2, b= 8, c= -384.
∏¿∆v¿Êz¿Av…
™¿ƒ∆ÆU¿º¿ƒ: y = [-b + Ý= (-8-56)/4 =Ý -16 wÊP…∆√£¿z¿
®¡∫¿ƒ Iƒt ∏¿AS…ÂAi¿i¡U¿ƒ™¿≈¢ÆË. |
|
v¡º…:
(®¡∫¿ƒ)2+ (®¡∫¿ƒ)2 =
122+ 162 = 144+ 256 = 400 =202 .(´P¿t)2
∏¿™¿ƒ∏… •¿j∫¡g¿ ∏¿jAi¿i¡Vz….
2.19.1 ∏¿™¿ƒ∏…Â15:Ý Jg¿q¿ƒ •¿l÷tU¿º¿ £¿q¿ƒ´£¿ z¿∆g¿ 1200Q.´ƒ.. MAz¿ƒ
g… ƃU¡rAi¿ƒƒ F Jg¿q¿ƒ •¿l÷tU¿º¿ £¿q¿ƒ™… Nq¿ƒv¿€™…. g… ∞£¿ ™…√U¿™¿≈ ™…∆z¿∞£¿
™…√U¿QÃAv¿ 30Q.´ƒ./U¿A. ∫…Z¡—z¿g… Cz¿P…à Jg¿q¿ƒ U¿Am… ∏¿™¿ƒAi¿ƒ
P¿r™…ƒ ∏¡P¡U¿ƒv¿€z…. ∫¡U¡z¿g… g… ∞£¿ ™…∆z¿∞£¿ ™…√U¿ Jµ¿ƒ÷?
•¿j∫¡g¿:
g… ∞£¿ ™…∆z¿∞£¿ ™…√U¿ = xDVg¿∞.
Nq¿Æƒ ®…√P¡z¿ ∏¿™¿ƒAi¿ƒ = 1200/x U¿A.
™…√U¿™¿≈ 30 Q.´ƒ./U¿A.
∫…Z¡—z¿g… Jg¿q¿£…√ ™…√U¿z¿∞Ë ®…√P¡z¿ ∏¿™¿ƒAi¿ƒ = 1200/(x+30).U¿A.
∫…∆∏¿ ∏¿™¿ƒAi¿ƒ™¿≈ ™¿ƒƒAa£¿ ∏¿™¿ƒAi¿ƒQÃAv¿ 2 U¿Am…
P¿r™…ƒ.
![]() Ý1200/x-1200/(x+30) = 2
Ý1200/x-1200/(x+30) = 2
Z¿lƒ™¿nP…: ∏¿AP…Î√¶π, ∏¿∆v¿Ê G•¿Ai…∆√Vπ ™¿ƒ∆ÆU¿º¿£¿ƒþ
P¿Aq¿ƒªr¨ƒj: x=120
v¡º…:
1200/120 ñ 1200/150 = 10-8 =2 z¿v¡€A±¿.
2.19.1 ∏¿™¿ƒ∏… 16: Mß‚ £¡´P¿£¿ƒ MAz¿ƒ ™…∆√m¡g¿ƒ z…∆√t¬Ai¿ƒ£¿ƒþ Jg¿q¿ƒ
ßAz¿g¿ƒU¿º¿ £¿q¿ƒ™… Z¿Ø¡¨ƒ∏¿ƒv¡€£…. ßAz¿g¿ƒU¿º¿ £¿q¿ƒ´£¿ z¿∆g¿ 8 Q.´ƒ.
C™¿£¿ƒ MAz¿ƒ ßAz¿j§Az¿ ∫…∆g¿lƒ E£…∆þAz¿ƒ ßAz¿jU… ∫…∆√V •¿≈£¿B ™¡•¡∏¿ƒ ßg¿Æƒ 1U¿A
40§´ƒµ¿U¿º¿ƒ ®…√P¿ƒ. •¿Ê™¡∫¿z¿ ™…√U¿ U¿Am…U… 2
Q.´ƒ. Dz¿g…, §±¿—Æ §√j£¿∞Ë z…∆√t¬Ai¿ƒ ™…√U¿ Jµ¿ƒ÷?
[z…∆√t¬Ai¿ƒƒ •¿Ê™¡∫¿z¿ e…∆v…U…√ Z¿∞∏¿ƒ™¡U¿ ∏¿™¿ƒAi¿ƒ
P¿r™…ƒ ∏¡P¿ƒ. •¿Ê™¡∫¿z¿ ´g¿ƒz¿Þ Z¿∞∏¿ƒ™¡U¿ ∏¿™¿ƒAi¿ƒ e¡π€®…√P¿ƒ]
•¿j∫¡g¿:
z…∆√t¬Ai¿ƒ ™…√U¿ = xDVg¿∞ (§±¿—Æ
§√j£¿∞Ë)
∫…∆√V, ßg¿Æƒ ®…√P¡z¿ Mlƒ÷ ∏¿™¿ƒAi¿ƒÝ 1U¿A. 40§. =
100/60 = 5/3 U¿Am….
ßAz¿g¿ƒU¿º¿ £¿q¿ƒ´£¿ z¿∆g¿ = 8Q.´ƒ.
•¿Ê™¡∫¿z¿ ™…√U¿ 2Q.´ƒ/U¿A.
![]() •¿Ê™¡∫¿z¿ ¢Qã¿∞Ë ∫…∆√U¿Æƒ ®…√P¡z¿ P¡Æ = 8/x+2 (z…∆√t¬Ai¿ƒ ™…√U¿ + •¿Ê™¡∫¿z¿ ™…√U¿)
•¿Ê™¡∫¿z¿ ¢Qã¿∞Ë ∫…∆√U¿Æƒ ®…√P¡z¿ P¡Æ = 8/x+2 (z…∆√t¬Ai¿ƒ ™…√U¿ + •¿Ê™¡∫¿z¿ ™…√U¿)
![]() •¿Ê™¡∫¿z¿ ´g¿ƒz¿Þ ∫…∆√U¿Æƒ ®…√P¡z¿ P¡Æ = 8/x-2 (•¿Ê™¡∫¿™¿≈ ™…√U¿™¿£¿ƒþ P¿r™…ƒ ™¿i¡q¿ƒv¿€z…)
•¿Ê™¡∫¿z¿ ´g¿ƒz¿Þ ∫…∆√U¿Æƒ ®…√P¡z¿ P¡Æ = 8/x-2 (•¿Ê™¡∫¿™¿≈ ™…√U¿™¿£¿ƒþ P¿r™…ƒ ™¿i¡q¿ƒv¿€z…)
![]() Mlƒ÷ ∏¿™¿ƒAi¿ƒ = Ý8/(x-2) + 8/(x+2) = 5/3
Mlƒ÷ ∏¿™¿ƒAi¿ƒ = Ý8/(x-2) + 8/(x+2) = 5/3
Dz¿ƒz¿jAz¿ ©r∏¿®…√P¡z¿ƒð: Ý8/(x-2) +
8/(x+2) = 5/3
Z¿lƒ™¿nP…: ∏¿´ƒ√P¿g¿t™¿£¿ƒþ ∏¿ƒÆ©¸√P¿jπ, ∏¿∆v¿Ê G•¿Ai…∆√Vπ ™¿ƒ∆Æ
P¿Aq¿ƒ ªr¨ƒj x =10
v¡º…:
®…√P¡z¿ Mlƒ÷ P¡Æ = 8/(10-2) + 8/(10+2) = 8/8 + 8/12 = 1+2/3 = 5/3ÝÝ z¿v¡€A±¿
2.19.1 ∏¿™¿ƒ∏… 17: MAz¿ƒ ´™¿i¡£¿™¿≈ §U¿¢v¿ ∏¿™¿ƒAi¿ƒQÃAv¿ 30 §´ƒµ¿
v¿q¿™¡V ∫…∆g¿nv¿ƒ. Cz¿ƒ •¿Ai¿ƒt¬∏¿®…√P¡z¿ z¿∆g¿ 1500 Q.´ƒ. §U¿¢v¿
∏¿™¿ƒAi¿ƒP…Ã√ C∞ËU… v¿Æƒ•¿Æƒ Cz¿ƒ v¿£¿þ ™…√U¿™¿£¿ƒþ ™¿i¡™¿ƒ∆ƃ ™…√U¿QÃAv¿ 250Q.´ƒ.
£¿µ¿ƒ÷ ∫…a—∏¿®…√P¿ƒ. ∫¡U¡z¿g… Cz¿g¿ ™¿i¡™¿ƒ∆ƃ ™…√U¿ ™¿ƒv¿ƒ€ ™¿i¡™¿ƒ∆ƃ C™¿¢¸
P¿Aq¿ƒªr¨ƒj.
•¿j∫¡g¿:
´™¿i¡£¿z¿ §v¿Âz¿ ™…√U¿ = x DVg¿∞.
P¿Ê´ƒ∏¿®…√P¡z¿ z¿∆g¿ = 1500Q.´ƒ.
![]() Ý™¿i¡™¿ƒ∆∞ •¿ÊAi¿i¡tz¿ ∏¿™¿ƒAi¿ƒ = z¿∆g¿/ ™…√U¿ = 1500/x U¿Am….
Ý™¿i¡™¿ƒ∆∞ •¿ÊAi¿i¡tz¿ ∏¿™¿ƒAi¿ƒ = z¿∆g¿/ ™…√U¿ = 1500/x U¿Am….
´™¿i¡£¿™¿≈ Czs¿ U¿Am… v¿q¿™¡V ∫…∆g¿nz…. §U¿¢v¿
™…√º…U…√ U¿ƒj v¿Æƒ•¿Æƒ Cz¿ƒ v¿£¿þ ™…√U¿™¿£¿ƒþ ∫…a—πP…∆º¿ÓØ…√®…√P¿ƒ.
FU¿ ´™¿i¡£¿P…à •¿Ai¿ƒt¬∏¿Æƒ Eg¿ƒ™¿ ∏¿™¿ƒAi¿ƒ = (1500/x) -1/2
Ez…√ ∏¿™¿ƒAi¿ƒz¿∞Ë ´™¿i¡£¿ 1500 Q.´ƒ.
∫¡jz…. DU¿ ™…√U¿:Ý (x+250)
![]() Ý z¿∆g¿= ∏¿™¿ƒAi¿ƒ*∫…∆∏¿ ™…√U¿
Ý z¿∆g¿= ∏¿™¿ƒAi¿ƒ*∫…∆∏¿ ™…√U¿
I.e. 1500 = {(1500/x) -1/2}*(x+250) =
(3000-2x)*(x+250)/2x
I.e. 3000x = (3000-x)(x+250)
Cq¿ÿ U¿ƒu¡P¡g¿¢Az¿,
I.e. 3000x = 3000x -x2+750000-250x
I.e. x2-750000+250x =0
∏¿∆v¿Ê G•¿Ai…∆√Vπ: ![]() Ý= 1750
Ý= 1750
![]() Ý™¿ƒ∆ÆU¿º¿ƒ:
Ý™¿ƒ∆ÆU¿º¿ƒ:
x = [-b ![]()
![]() )]/2aÝÝÝ = (-250
)]/2aÝÝÝ = (-250 ![]() 1750)/2
1750)/2
x = 750 Cx¿™¡ x =-1000
´™¿i¡£¿z¿ ™…√U¿ Iƒt ®…Ø… Cx¿´ÆËz¿ƒð x = 750Q.´ƒ/U¿Am…
![]() Ý™¿i¡™¿ƒ∆∞ •¿ÊAi¿i¡tz¿ ∏¿™¿ƒAi¿ƒ= 1500/750 = 2U¿Am…
Ý™¿i¡™¿ƒ∆∞ •¿ÊAi¿i¡tz¿ ∏¿™¿ƒAi¿ƒ= 1500/750 = 2U¿Am…
v¡º…:
´™¿i¡£¿z¿ ™…√U¿ 250Q.´ƒ.
∫…Z¡—z¿ƒz¿jAz¿ ∫…∆∏¿ ™…√U¿: 1000Q.´ƒ. /U¿Am….
![]() Ý1500Q.´ƒ. P¿Ê´ƒ∏¿Æƒ ®…√P¡z¿ ∏¿™¿ƒAi¿ƒ = 1500/1000 = 1.5 U¿Am…. CAz¿g…
Ý1500Q.´ƒ. P¿Ê´ƒ∏¿Æƒ ®…√P¡z¿ ∏¿™¿ƒAi¿ƒ = 1500/1000 = 1.5 U¿Am…. CAz¿g…
§U¿¢v¿ •¿ÊAi¿i¡tz¿ ™…√º…VAv¿ Ω U¿Am…
P¿r™…ƒ.
´™¿i¡£¿™¿≈ Ω U¿Am… v¿q¿™¡V
∫…∆g¿ng¿ƒ™¿≈z¿jAz¿, ∏¿jAi¿i¡z¿ ™…√º…U…√ U¿ƒjAi¿ƒ£¿ƒþ v¿Æ•¿≈v¿€z…. ∏¿™¿ƒ∏…Â
•¿j∫¡g¿ ∏¿jAi¿i¡Vz….
2.19.1 ∏¿™¿ƒ∏… 18: K ∫¿ƒq¿ƒV, ∫¿A∏¿U¿º¿ U¿ƒA¶£¿ Mlƒ÷ ∫¿A∏¿U¿º¿
™¿U¿™¿ƒ∆Æz¿ 7/2 g¿µ¿ƒ÷ ∫¿A∏¿U¿º¿ƒ P…∆º¿z¿ z¿q¿z¿∞Ë Dq¿ƒw€™…. GΩz…g¿q¿ƒ
∫¿A∏¿U¿º¿ƒ P…∆º¿z¿∞Ë dU¿º¿™¡q¿ƒw€™…. ∫¡U¡z¿g… Mlƒ÷ Eg¿ƒ™¿ ∫¿A∏¿U¿º…µ¿ƒ÷? (∞√Ø¡™¿w ±…∆Ë√P¿ 70)
•¿j∫¡g¿:
Mlƒ÷ ∫¿A∏¿U¿º¿ ∏¿AS… x DVg¿∞.
z¿q¿z¿∞Ë Dq¿ƒw€g¿ƒ™¿ ∫¿A∏¿U¿º¿ƒ = (7/2)![]()
P…∆º¿z¿∞Ë dU¿º¿™¡q¿ƒ™¿ ∫¿A∏¿U¿º¿ƒ = 2
![]() Ýx= (7/2)
Ýx= (7/2)![]() +2
+2
F ∏¿´ƒ√P¿g¿t™¿£¿ƒþ ©rπz¡U¿, ™¿ƒ∆ÆU¿º¿ƒ: 1/4 Cx¿™¡
16
Dz¿g… ∫¿A∏¿U¿º¿ ∏¿AS… 1/4 Eg¿Ø¡U¿z¿ƒ.
Mlƒ÷ Eg¿ƒ™¿ ∫¿A∏¿U¿º¿ƒ = 16
v¡º…:
16 = 14+2 = (7/2) ![]() +2 ∏¿™¿ƒ∏…ÂAi¿ƒ∞Ë P…∆l÷Av…Ai…ƒ√ Ez….
+2 ∏¿™¿ƒ∏…ÂAi¿ƒ∞Ë P…∆l÷Av…Ai…ƒ√ Ez….
2.19.1 ∏¿™¿ƒ∏… 19: Cdƒ£¿£¿ƒ ™¿ƒ∫¡®s¡g¿v¿ Ai¿ƒƒz¿Þz¿∞Ë P¿t£¿£¿ƒþ
P…∆ÆËƃ ßv¿€ΩP… ¨ƒAz¿ ∫¿Æ™¿≈ ®¡tU¿º¿£¿ƒþ v…U…Ai¿ƒƒv¡€£…. v…U…z¿ ®¡tU¿º¿∞Ë Czs¿z¿µ¿÷jAz¿
P¿t£¿ ®¡tU¿º¿£¿ƒþ v¿ƒAq¿j∏¿ƒv¡€£…. v…U…z¿ ®¡tU¿º¿ ™¿U¿™¿ƒ∆Æz¿ 4 g¿µ¿÷jAz¿ P¿t£¿ P¿ƒz¿ƒg…U¿º¿£¿ƒþ, 6 ®¡tU¿ΩAz¿ ±¿Æ£¿£¿ƒþ, MAz…∆Az¿jAz¿ P¿t£¿
g¿x¿z¿ P…∆q…, P¿t£¿ g¿x¿z¿ ®¡™¿≈l, ™¿ƒv¿ƒ€ P¿t£¿ ©ÆË£¿ƒþ v¿ƒAq¿j∏¿ƒv¡€£….
GΩz¿ MAz¿ƒ ®¡t¢Az¿ P¿t£¿£¿ƒþ P…∆Az¿g…, ßv¿€ΩP… ¨ƒAz¿ Mlƒ÷ Jµ¿ƒ÷ ®¡tU¿º¿£¿ƒþ
v…U…Ai¿ƒƒv¡€£…? (∞√Ø¡™¿w: ±…∆Ë√P¿ 71)
•¿j∫¡g¿:
v…U…z¿
®¡tU¿º¿ Mlƒ÷ ∏¿AS… x
Eg¿∞. Ý
|
∫¿Av¿ |
Kv¿P…Ã |
Jµ¿ƒ÷ |
|
1 |
P¿t£¿ ®¡tU¿º¿£¿ƒþ
P¿v¿€j∏¿Æƒ |
(x/2) |
|
2 |
P¿t£¿ P¿ƒz¿ƒg…U¿ΩU¡V |
4 |
|
3 |
±¿Æ§U… |
6 |
|
4 |
g¿x¿z¿
P…∆q…,®¡™¿≈l,P¿t£¿ ©ÆƒËU¿ΩU… |
(1+1+1) =3 |
|
5 |
P¿t£¿ ™…ƒ√Ø… |
1 |
![]() x = (x/2)+ 4
x = (x/2)+ 4 ![]() +6+3+1
+6+3+1
![]() Ýx ñ(x/2)-10 = 4
Ýx ñ(x/2)-10 = 4 ![]()
![]() Ý(x/2)-10 = 4
Ý(x/2)-10 = 4 ![]()
![]() Ý(x-20) = 8
Ý(x-20) = 8 ![]()
![]() Ýx2-40x+400
= 64x ÝÝ--------ý ((a+b)2Ý ∏¿∆v¿Ê G•¿Ai…∆√Vπz…).
Ýx2-40x+400
= 64x ÝÝ--------ý ((a+b)2Ý ∏¿∆v¿Ê G•¿Ai…∆√Vπz…).
![]() Ýx2-104x+400
=0
Ýx2-104x+400
=0
![]() Ý(x-100)*(x-4) =0
Ý(x-100)*(x-4) =0
![]() Ýx=100Ý Cx¿™¡ÝÝ x=4
Ýx=100Ý Cx¿™¡ÝÝ x=4
(C™¿£¿ƒ 6
®¡tU¿º¿£¿ƒþ ±¿Æ§U… G•¿Ai…∆√Vπg¿ƒ™¿≈z¿jAz¿ 4 ∏¡zs¿Â´ÆË)
Dz¿ƒz¿jAz¿ Cdƒ£¿£¿ƒ 100 ®¡tU¿º¿£¿ƒþ v…U…¢g¿ƒv¡€£…
v¡º…:
100= 50+40+6+3+1
2.19.1 ∏¿™¿ƒ∏… 20:MAz¿ƒ P¡r£¿ ™¿ƒzs¿Âz¿∞Ë ™¿ƒAU¿U¿º¿ U¿ƒA¶£¿ 1/5 £…√ ®s¡U¿z¿∞Ë 3 £¿ƒþ P¿º…z¿ƒ ™¿Vπz¿ U¿ƒA•¿≈ U¿ƒ∫…U… ∫…∆√¨ƒv¿ƒ. GΩz¿ MAz¿ƒ
™¿ƒg¿z¿ g…A®…Ai¿ƒ£¿ƒþ ∫¿w€v¿ƒ. ™¿ƒAU¿U¿º¿ Mlƒ÷ ∏¿AS… Jµ¿ƒ÷? (®s¡∏¿Ãg¿ :
©√dU¿t¬v¿)
•¿j∫¡g¿:
™¿ƒAU¿U¿º¿
Mlƒ÷ ∏¿AS… x
Eg¿∞.Ý
|
∫¿Av¿ |
J∞Ë |
Jµ¿ƒ÷ |
|
1 |
U¿ƒ∫…U… |
{(x/5)-3}2 |
|
2 |
GΩz¿z¿ƒð |
1 |
Ý
![]() {(x/5)-3}2+1 =x
{(x/5)-3}2+1 =x
![]() (x2/25) ñ(6x/5)+9+1=x
(x2/25) ñ(6x/5)+9+1=x
![]() (x2/25) ñ(11x/5)+10=0
(x2/25) ñ(11x/5)+10=0
![]() x2ñ55x+250=0
x2ñ55x+250=0
![]() (x-50)*(x-5) =0
(x-50)*(x-5) =0
![]() Ýx=50 Cx¿™¡Ý
x=5: Ý5 ∏¡zs¿Â´ÆË KP¿Az¿g… {(x/5)-3}
Iƒt DU¿®¡g¿z¿ƒ
Ýx=50 Cx¿™¡Ý
x=5: Ý5 ∏¡zs¿Â´ÆË KP¿Az¿g… {(x/5)-3}
Iƒt DU¿®¡g¿z¿ƒ
v¡º…:
50= (10-3)2+1= 49+1,
2.19.2 ™¿U¿
∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿ ∏¿È®s¡™¿(Nature of roots of a Quadratic equation)
§√™¿≈ F™¿g…U… ∏¿™¿ƒ∏…ÂU¿º¿£¿ƒþ
©r∏¿ƒ™¡U¿ b2-4ac Ai¿ƒ ®…Ø…U¿º¿£¿ƒþ U¿™¿ƒ§π¢ð√g¡?
2.19.1 .5g¿∞Ë b2-4ac
= 0 ™¿ƒ∆ÆU¿º¿ƒ •¿g¿∏¿ýg¿ ∏¿™¿ƒ.
2.19.1 .8g¿∞ b2-4ac <0 ™¿ƒ∆ÆU¿º¿ƒ C™¡∏¿€´P¿ ∏¿AS…ÂU¿º¿ƒ.
GΩz¿™¿≈U¿º¿∞Ë b2-4ac > 0 ™¿ƒ∆ÆU¿º¿ƒ ™¡∏¿€´P¿ ∏¿AS…ÂU¿º¿ƒ.
™¿U¿ ∏¿´ƒ√P¿g¿tU¿º¿∞Ë F b2-4acAi¿ƒ£¿ƒþÝ ì±…∆√zs¿£¿î
(discriminant)Ý J£¿ƒþv…€√™…. Ez¿£¿ƒþ ![]() (q…Ø¡÷) ¢Az¿
∏¿∆a∏¿ƒv…€√™….
(q…Ø¡÷) ¢Az¿
∏¿∆a∏¿ƒv…€√™….
£¡´√U¿ F w√™¿i¡£¿P…à ßg¿ƒv…€√™….
|
|
±…∆√zs¿P¿z¿ ®…Ø… (b2-4ac)
= |
™¿ƒ∆ÆU¿º¿ ∏¿È®s¡™¿=[-b |
|
1 |
|
™¿ƒ∆ÆU¿º¿ƒ ™¡∏¿€™¿ ™¿ƒv¿ƒ€ ∏¿™¿ƒ. |
|
2 |
|
™¿ƒ∆ÆU¿º¿ƒ
™¡∏¿€™¿∏¿AS…ÂU¿º¿ƒ ™¿ƒv¿ƒ€ ©¸£¿þ™¡Vg¿ƒv¿€z…. |
|
3 |
|
™¿ƒ∆ÆU¿º¿ƒ ∏¿™¿ƒ™¿ÆËz¿ C™¡∏¿€´P¿ ∏¿AS…ÂU¿º¿ƒ (∏¿´ƒ‰±¿Ê ∏¿AS…ÂU¿º¿ƒ) |
2.19.2 ∏¿™¿ƒ∏… 1: Ým£¿ Ai¿i¡™¿ zs¿£¿ ®…Ø…U… mk2-3k+1 =0 Ai¿ƒ
™¿ƒ∆ÆU¿º¿ƒ (1) ∏¿™¿ƒÝ (2) ™¡∏¿€™¿ ™¿ƒv¿ƒ€ ©¸£¿þ (3)C™¡∏¿€™¿ ™¿ƒv¿ƒ€ ©¸£¿þ?
•¿j∫¡g¿:
∏¿´ƒ√P¿g¿t: mk2-3k+1 =0
E∞Ë a=m, b=
-3, c= 1
![]() Ýb2-4ac = 9Ý ñ 4m
Ýb2-4ac = 9Ý ñ 4m
1. ™¿ƒ∆ÆU¿º¿ƒ
∏¿™¿ƒ™¡U¿®…√P¡z¿g…, b2-4ac
=0
(I.e. 9-4m =0, i.e. m = 9/4)
2. ™¿ƒ∆ÆU¿º¿ƒ
™¡∏¿€™¿ ™¿ƒv¿ƒ€ ©¸£¿þ™¡U¿®…√P¡z¿g…, Ýb2-4ac >0
(I.e. 9-4m >0, i.e. 9 >4m, i.e. m < 9/4)
3. ™¿ƒ∆ÆU¿º¿ƒ
C™¡∏¿€™¿ ™¿ƒv¿ƒ€ ©¸£¿þ™¡Vg¿®…√P¡z¿g…,
Ýb2-4ac <0
(I.e. 9-4m <0, i.e. 9 <4m, i.e. m > 9/4)
2.19.2 ∏¿™¿ƒ∏… 2: m£¿
Ai¿i¡™¿ ®…Ø…U… r2-(m+1)r
+4 =0 ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿ƒ (∏¿™¿ƒ),
(™¡∏¿€™¿ ™¿ƒv¿ƒ€ ©¸£¿þ), (C™¡∏¿€™¿ ™¿ƒv¿ƒ€ ©¸£¿þ)
•¿j∫¡g¿:
∏¿´ƒ√P¿g¿t: r2-(m+1)r +4 =0
E∞Ë a=1, b=
-(m+1), c= 4
![]() Ýb2-4ac = (m+1) 2-16
Ýb2-4ac = (m+1) 2-16
= [(m+1)+4]*[(m+1)-4]Ý ===> (C•¿™¿wπz¡U¿)
= (m+5)(m-3)
1. ™¿ƒ∆ÆU¿º¿ƒ
∏¿™¿ƒ™¡U¿®…√P¡z¿g…, Ýb2-4ac =0
(i.e. (m+5)= 0 Cx¿™¡ (m-3)=0 i.e. m=-5 Cx¿™¡ m=3)
2. ™¿ƒ∆ÆU¿º¿ƒ
™¡∏¿€™¿ ™¿ƒv¿ƒ€ ©¸£¿þ™¡U¿Æƒ, b2-4ac
>0
(i.e. (m+5)(m-3) >0)
Jg¿q¿ƒ •¿z¿U¿º¿ U¿ƒtÆßÞ zs¿£¿™¡Vz¿ðg… Jg¿q¿∆ •¿z¿U¿º¿ƒ zs¿£¿™¡Vg¿®…√P¿ƒ EÆË
Jg¿q¿∆ •¿z¿U¿º¿ƒ Iƒt™¡Vg¿®…√P¿ƒ J£¿ƒþ™¿≈z¿£¿ƒþ U¿™¿ƒ§πz¡U¿,Jg¿q¿ƒ
∏¿Az¿®s¿U¿º¿ƒ ∏¡zs¿Â:ÝÝÝÝÝÝÝÝÝÝÝÝ
∏¿Az¿®s¿ 1: m+5 > 0 ™¿ƒv¿ƒ€ m-3>0
I.e.ÝÝ m> -5Ý ™¿ƒv¿ƒ€ m>3: ª√Vg¿Æƒ m>3 DVg¿Ø…√ ®…√P¿ƒ
∏¿Az¿®s¿ 2: m+5 < 0 ™¿ƒv¿ƒ€ Ým-3<0
I.e.ÝÝ m< -5 ™¿ƒv¿ƒ€ m<3: ª√Vg¿Æƒ m<-5 DVg¿Ø…√ ®…√P¿ƒ
3. ™¿ƒ∆ÆU¿º¿ƒ
C™¡∏¿€™¿ ™¿ƒv¿ƒ€ ©¸£¿þ™¡U¿Æƒ, b2-4ac
<0
(i.e. (m+5)(m-3) <0)
Jg¿q¿ƒ •¿z¿U¿º¿ U¿ƒtÆßÞ Iƒt™¡Vz¿ðg… MAz¿ƒ •¿z¿ zs¿£¿™¡Vz¿ƒð E£…∆þAz¿ƒ
Iƒt™¡Vg¿®…√P¿ƒ J£¿ƒþ™¿≈z¿£¿ƒþ U¿™¿ƒ§πz¡U¿,Jg¿q¿ƒ ∏¿Az¿®s¿U¿º¿ƒ ∏¡zs¿Â:ÝÝ
∏¿Az¿®s¿ 1: m+5 < 0 ™¿ƒv¿ƒ€ Ým-3>0
I.e.ÝÝ m< -5Ý ™¿ƒv¿ƒ€ m>3: ÝEz¿ƒ ∏¡zs¿Â´ÆË
∏¿Az¿®s¿ 2: m+5 > 0 ™¿ƒv¿ƒ€ m-3<0
I.e.ÝÝ m< -5Ý ™¿ƒv¿ƒ€ m<3: ª√Vg¿Æƒ mÝ -5
Ý™¿ƒv¿ƒ€ 3 Ýg¿ ™¿ƒzs¿Â Eg¿Ø…√®…√P¿ƒ.
F j√w £¡™¿≈ P¿Aq¿ƒ ªr¢g¿ƒ™¿≈z¿£¿ƒþ ∏¿AS¡Âg…√S…Ai¿ƒ ™…ƒ√Ø… P…º¿U…
P¡t¬πz¿Av… U¿ƒg¿ƒw∏¿ß∫¿ƒz¿ƒ.

2.19.2 ∏¿™¿ƒ∏… 3:Ý (p+1) n2+2(p+3)n +(p+8) =0Ý
F ∏¿´ƒ√P¿g¿tz¿
™¿ƒ∆ÆU¿º¿ƒ ∏¿™¿ƒ™¡U¿®…√P¡z¿g…, pAi¿ƒ ®…Ø… P¿Aq¿ƒªr.
•¿j∫¡g¿:
z¿v¿€ ∏¿´ƒ√P¿g¿t™¿≈ ax2 +bx+ c =0 g¿∆•¿z¿∞Ëz….
a=(p+1), b= 2p+6, c= p+8
![]() Ýb2-4ac = (2p+6)2 Ýñ 4*(p+1)(p+8)
Ýb2-4ac = (2p+6)2 Ýñ 4*(p+1)(p+8)
ÝÝ =Ý (4p2+24p+36) -4(p2+8p+p+8)
ÝÝ = 4p2+24p+36
-4p2-36p-32
ÝÝ =-12p+4
™¿ƒ∆ÆU¿º¿ƒ ∏¿™¿ƒ™¡U¿®…√P¡z¿g…, Ýb2-4ac =0
I.e.ÝÝ -12p+4 = 0
I.e. p=1/3
∏¿∆v¿Êz¿Av…, p=1/3Ý Dz¡U¿ ™¿ƒ∆ÆU¿º¿ƒ:
n = [-b ![]()
![]() ]/2aÝ =[-2(p+3)
]/2aÝ =[-2(p+3)![]() 0)
]/2(p+1)Ý =Ý - (p+3)/(p+1)
0)
]/2(p+1)Ý =Ý - (p+3)/(p+1)
ÝÝÝÝÝÝÝÝÝÝ = - (10/3)/(4/3) = -5/2
v¡º…:
n = -5/2 £¿þ ∏¿´ƒ√P¿g¿tz¿∞Ë Dz…√≤π,ÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝ
ÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝÝ
(p+1) n2+2(p+3)n +(p+8)
= 25(p+1)/4 -5(p+3) +(p+8)
= 25(p+1)/4Ý -4p
-7
= (25p+25-16p-28)/4
= (9p-3)/4ÝÝ (p
= 1/3 Dz…√≤π)
=0/4 = 0 = ßÆ®s¡U¿
2.19.2 ∏¿™¿ƒ∏… 4: (3p+1)c2+2(p+1)c+p=0 ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿ƒ ∏¿™¿ƒ™¡U¿®…√P¡z¿g….
ëpíAi¿ƒ ®…Ø… P¿Aq¿ƒªr.
•¿j∫¡g¿:
∏¿´ƒ√P¿g¿t™¿≈ ax2 +bx+ c =0
E∞Ë a=(3p+1), b= 2p+2, c= p
![]() Ýb2-4ac = (2p+2)2 Ýñ 4*(3p+1)p
Ýb2-4ac = (2p+2)2 Ýñ 4*(3p+1)p
ÝÝ =Ý (4p2+4+8p) -4(3p2+p)
ÝÝ = 4p2+4+8p
-12p2-4p
ÝÝ = -8p2+4p+4
ÝÝ = - 4(2p2-p-1)
∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿ƒ ∏¿™¿ƒ™¡U¿®…√P¡z¿g…, Ýb2-4ac
=0
![]() Ý2p2-p-1 = 0
Ý2p2-p-1 = 0
Jq¿ß¢ = 2p2-2p+p-1
Ý =
2p(p-1)+(p-1)
Ý = (p-1)(2p+1)
FU¿ 2p2-p-1 = 0 Dz¿ðjAz¿ (p-1)(2p+1) = 0
![]() Ý p=1 Cx¿™¡ p= -1/2
Ý p=1 Cx¿™¡ p= -1/2
U¿™¿ƒ§π: 2p2-p-1
= 0 Ez¿g¿ ™¿ƒ∆ÆU¿º¿£¿ƒþ P¿Aq¿ƒªrAi¿ƒÆƒ
C•¿™¿v¿£¿ ´zs¡£¿ G•¿Ai…∆√Vπz…ð√™…. ∏¿∆v¿Êz¿Av… p=1 Dz¡U¿,
™¿ƒ∆ÆU¿º¿ƒ:
c = [-b +![]() ]/2aÝ =[-2p-2
]/2aÝ =[-2p-2 ![]() 0)
]/2(3p+1)Ý =Ý - 4/8 =Ý
-1/2
0)
]/2(3p+1)Ý =Ý - 4/8 =Ý
-1/2
p = -1/2 Dz¡U¿ c U…
E£…∆þAz¿ƒ ®…Ø… (Cz…√) ßg¿ƒv¿€z….
U¿™¿ƒ§π: ∏¿∆v¿Ê™¿£¿ƒþ
Jg¿q¿ƒ ®¡j G•¿Ai…∆√VπAi¿ƒ∆ ™…ƒ√∞£¿ ∏¿´ƒ√P¿g¿t™¿£¿ƒþ ©rπ ëpíAi¿ƒ ®…Ø…
P¿Aq¿ƒªrAi¿ƒß∫¿ƒz¿ƒ.
v¡º…:
∏¿´ƒ√P¿g¿tz¿∞Ë c = -1/2 Dz…√≤πz¡U¿,
(3p+1) c2+2(p+1)c +p
= (3p+1)/4+2(p+1)(-1/2) +p
=(3p+1)/4 ñ(p+1) +p
=(3p+1)/4 -1 (4 £¿þ ∏¡™¿i¡£¿Â b…√z¿ ™¿i¡r)
= [(3p+1) -4]/4 (p =1 Dz…√≤π)
= 0/4 = 0 = z¿v¿€ ∏¿´ƒ√P¿g¿tz¿ ßÆߢ.
Z¿lƒ™¿nP…: p = -1/2ÝÝ Dz¡U¿, (3p+1) c2+2(p+1)c
+p =0 ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿ƒ
∏¿™¿ƒ™¡V™…Ai…ƒ√ •¿j√QÎπ.
2.19.2 ∏¿™¿ƒ∏… 5: 2y2-py +1 =0 ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿ƒ ∏¿™¿ƒ™¡Vz¿ðg…. ëpíAi¿ƒ
®…Ø… P¿Aq¿ƒªr.
•¿j∫¡g¿:
z¿v¿€ ∏¿´ƒ√P¿g¿t™¿≈ ax2 +bx+ c =0 g¿∆•¿z¿∞Ëz….
E∞Ë a=2, b= -p, c= 1
![]() Ýb2-4ac = p2 -8
Ýb2-4ac = p2 -8
™¿ƒ∆ÆU¿º¿ƒ ∏¿™¿ƒ™¡Vg¿Æƒ, b2-4ac =0
p2 = 8 :
p = ![]() Ý2
Ý2![]()
Z¿lƒ™¿nP…: p Ai¿ƒ
F ®…Ø…Ai¿ƒƒ ∏¿™¿i¡£¿ ™¿ƒ∆ÆU¿º¿£¿ƒþ P…∆q¿ƒv¿€z…Az¿ƒ v¡º…£…∆√r.
2.19.3 ™¿U¿ ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿ΩU¿∆, C™¿≈U¿º¿
∏¿∫¡•¿™¿v¿£¿U¿ΩU¿∆ Eg¿ƒ™¿ ∏¿AßAzs¿(Relationship between roots and co-efficients):
ÝëmíÝ ™¿ƒv¿ƒ€ ëní U¿º¿ƒ ™¿U¿∏¿´ƒ√P¿g¿t ax2 +bx+ c =0 Ez¿g¿ ™¿ƒ∆ÆU¿º¡Vg¿∞.
![]() Ý(x-m)(x-n) = 0
Ý(x-m)(x-n) = 0
™¿U¿ ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿ƒ(m,n) :
x = [-b +![]() ]/2aÝ Cx¿™¡ x = [-b -
]/2aÝ Cx¿™¡ x = [-b -![]() ]/2aÝÝÝ
]/2aÝÝÝ
![]() Ým = [-b +
Ým = [-b +![]() ]/2a
]/2a
ÝÝÝ nÝ = [-b -![]() ]/2a
]/2a
![]() Ým+n = [-b +
Ým+n = [-b +![]() ]/2a + [-b -
]/2a + [-b -![]() ]/2a
]/2a
= -2b/2a = -b/a
mn = [-b +![]() ]/2a * [-b -
]/2a * [-b -![]() ]/2a (
(a+b)(a-b) ∏¿∆v¿Ê
G•¿Ai…∆√Vπz…)
]/2a (
(a+b)(a-b) ∏¿∆v¿Ê
G•¿Ai…∆√Vπz…)
= [ (-b)2- {![]() }2] /4a2
}2] /4a2
= [b2 -(b2-4ac) ] /4a2
= 4ac/4a2
= c/a
w√™¿i¡£¿:
1) MAz¿ƒ
™¿U¿ ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿ ™…∆v¿€ = -b/a
2) MAz¿ƒ
™¿U¿ ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿ U¿ƒtÆßÞ = c/a
2.19.3 ∏¿™¿ƒ∏… 1: Ýx2 +(ab)x+ (a+b) =0 F ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿ ™…∆v¿€ ™¿ƒv¿ƒ€ U¿ƒtÆßÞ
P¿Aq¿ƒªr.
•¿j∫¡g¿:
z¿v¿€ ∏¿´ƒ√P¿g¿t™¿≈ ax2 +bx+ c =0 g¿∆•¿z¿∞Ëz….
E∞Ë a=1, b= ab, c= (a+b)
![]() m+n = -b/a = -ab/1 = -ab
m+n = -b/a = -ab/1 = -ab
Ýmn =c/a =(a+b)/1 = (a+b)
2.19.2 ∏¿™¿ƒ∏… 2: pr2 = r-5 F
∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿ ™…∆v¿€ ™¿ƒv¿ƒ€ U¿ƒtÆßÞ P¿Aq¿ƒªr.
•¿j∫¡g¿:
∏¿´ƒ√P¿g¿t pr2 ñr+5= 0
F ∏¿´ƒ√P¿g¿t™¿≈ a x2
+bx+ c =0 g¿∆•¿z¿∞Ëz….
E∞Ë a=p, b= -1, c= 5
![]() m+n = -b/a = 1/pÝ
m+n = -b/a = 1/pÝ
mn =c/a = 5/p
2.19.4 z¿v¿€ ™¿ƒ∆ÆU¿º¿£¿ƒþ ∫…∆A¢g¿ƒ™¿ ™¿U¿ ∏¿´ƒ√P¿g¿t™¿£¿ƒþ
g¿a∏¿ƒ™¿≈z¿ƒ (Formation of equation with given roots):
ëmíÝ ™¿ƒv¿ƒ€ ëní U¿º¿ƒ ™¿U¿
∏¿´ƒ√P¿g¿t ax2 +bx+ c =0 Ez¿g¿ ™¿ƒ∆ÆU¿º¡Vg¿∞. DU¿Ý (x-m)(x-n) = 0
Dz¿g… (x-m)(x-n)
=x(x-n)-m(x-n)
= x2 ñxn ñmx +mn
= x2 ñx(n+m) +mn
= x2 ñ( m+n)x +mn
™¿U¿ ∏¿´ƒ√P¿g¿tz¿ ∏¡™¿i¡£¿Â g¿∆•¿:-
Ýx2 ñ(™¿ƒ∆ÆU¿º¿ ™…∆v¿€)x +(™¿ƒ∆ÆU¿º¿
U¿ƒtÆßÞ) =0
2.19.3 ∏¿™¿ƒ∏… 1: 2a2-4a+1=0 F
∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿ƒ Ýëpí ™¿ƒv¿ƒ€ ëqí Dz¿g…, (p+q)2+4pq ™¿ƒv¿ƒ€ (p3 +q3)U¿º¿ ®…Ø… P¿Aq¿ƒªr¨ƒj ™¿ƒv¿ƒ€ Ýp3 ™¿ƒv¿ƒ€ q3U¿º¿ƒ
™¿ƒ∆ÆU¿º¡U¿ƒ™¿Av… ™¿U¿ ∏¿´ƒ√P¿g¿t ßg….
•¿j∫¡g¿:
z¿v¿€ ∏¿´ƒ√P¿g¿t™¿≈ ax2+bx+ c =0 g¿∆•¿z¿∞Ëz….
E∞Ë a=2, b= -4, c= 1
![]() p+q = -b/a = 4/2 =2ÝÝ
p+q = -b/a = 4/2 =2ÝÝ
ÝÝÝ pq =c/a =1/2
![]() Ý(p+q)2+4pq=4+2 = 6
Ý(p+q)2+4pq=4+2 = 6
£¿™¿ƒU… MAz¿ƒ ∏¿∆v¿Ê U…∆w€z…: a3+b3= (a+b) (a2+b2-ab)
![]() p3 +q3Ý
p3 +q3Ý
= (p+q)( p2+q2-pq)
= (p+q)[( p2+q2+2pq) -3pq)]
= (p+q)[( p+q)2-3pq]
=2*[4-3/2] = 5 ( (p+q) ™¿ƒv¿ƒ€ pqU¿º¿ ®…Ø…
Dz…√≤πz…)
£¿™¿ƒV√U¿ p3 ™¿ƒv¿ƒ€ q3U¿º¿ƒ
™¿ƒ∆ÆU¿º¡Vg¿ƒ™¿ ™¿U¿ ∏¿´ƒ√P¿g¿t ®…√P¿ƒ.
™¿ƒ∆ÆU¿º¿ ™…∆v¿€ = p3
+q3Ý =5 ( ™…ƒ√Ø… Ø…P¡ÃZ¡g¿ ™¿i¡rz…)
™¿ƒ∆ÆU¿º¿ U¿ƒtÆßÞ = p3*q3Ý = (pq)3 =(1/2)3 =1/8
![]() ®…√P¡z¿ ∏¿´ƒ√P¿g¿t:
®…√P¡z¿ ∏¿´ƒ√P¿g¿t:
x2-(™¿ƒ∆ÆU¿º¿
™…∆v¿€)x+ (™¿ƒ∆ÆU¿º¿ U¿ƒtÆßÞ)= 0
I.e. x2-5x+ 1/8= 0 (8 jAz¿ U¿ƒt¬π)
8x2-40x+1=0
2.19.3 ∏¿™¿ƒ∏… 2:Ý
™¿ƒ∆ÆU¿º¿ƒ p/q ™¿ƒv¿ƒ€
q/p Eg¿ƒ™¿Av… ™¿U¿ ∏¿´ƒ√P¿g¿t g¿aπ.
•¿j∫¡g¿:
ÝÝÝ m =p/q, n=q/p
![]() m+n = p/q+q/p = (p2+q2)/pq
m+n = p/q+q/p = (p2+q2)/pq
ÝÝÝ mn = p/q*q/p =1
![]() ™¿U¿ ∏¿´ƒ√P¿g¿tz¿ Dz¿±¿ g¿∆•¿: x2 ñ(n+m)x +mn= 0
™¿U¿ ∏¿´ƒ√P¿g¿tz¿ Dz¿±¿ g¿∆•¿: x2 ñ(n+m)x +mn= 0
I.e. x2 ñ(p2+q2)x/pq +1 = 0
Ý(pqx2 ñ(p2+q2)x
+pq)/pq =0(pq ∏¡™¿i¡£¿Â b…√z¿
™¿i¡rz…)
I.e. pqx2 ñ(p2+q2)x
+pq=0
2.19.3 ∏¿™¿ƒ∏… 3: x2+px+q=0 ∏¿´ƒ√P¿g¿tz¿
MAz¿ƒ ™¿ƒ∆Æ™¿≈ ™¿ƒv…∆€Az¿ƒ ™¿ƒ∆Æz¿ ™¿ƒ∆g¿g¿∂÷÷z¿ðg…. 3p2=16q JAz¿ƒ ∏¡¢¸π.
•¿j∫¡g¿:
z¿v¿€ ∏¿´ƒ√P¿g¿t™¿≈ ax2+bx+ c =0 g¿∆•¿z¿∞Ëz….
E∞Ë a=1,b=p,c=q
m ™¿ƒv¿ƒ€ n U¿º¿ƒ
∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¡Vg¿∞.
![]() m+n = -b/a = - pÝÝ
mn = c/a = q
m+n = -b/a = - pÝÝ
mn = c/a = q
MAz¿ƒ ™¿ƒ∆Æ™¿≈ ™¿ƒv…∆€Az¿g¿ 3 g¿∂÷z… ![]() Ým =3n DVg¿∞.
Ým =3n DVg¿∞.
![]() Ýp = - (m+n) =-(3n+n)= -4nÝÝ ™¿ƒv¿ƒ€ q =mn=3n*n = 3n2
Ýp = - (m+n) =-(3n+n)= -4nÝÝ ™¿ƒv¿ƒ€ q =mn=3n*n = 3n2
![]() Ý3p2= 3(-4n)2=
48n2=16*3n2 =
16q(
Ý3p2= 3(-4n)2=
48n2=16*3n2 =
16q(![]() 3n2=q)
3n2=q)
2.19.3 ∏¿™¿ƒ∏… 4: 4x2-8px+9=0 ∏¿´ƒ√P¿g¿tz¿
™¿ƒ∆ÆU¿º¿ £¿q¿ƒ´£¿ ™¿Âv¡Â∏¿ 4 Dz¿g… ëpí Ai¿ƒ ®…Ø…Ai¿ƒ£¿ƒþ P¿Aq¿ƒªr¨ƒj.
•¿j∫¡g¿:
z¿v¿€ ∏¿´ƒ√P¿g¿t™¿≈ ax2+bx+ c =0 g¿∆•¿z¿∞Ëz….
E∞Ë a=4,b=-8p,c=9
m ™¿ƒv¿ƒ€ n U¿º¿ƒ
∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¡Vg¿∞.
1) m+n = -b/a = 8p/4 = 2pÝ ===Ë(1)
2)Ý mn= c/a = 9/4ÝÝÝÝÝÝÝÝÝÝÝÝÝ ===Ë(2)
™¿ƒ∆ÆU¿º¿ £¿q¿ƒ´£¿ ™¿Âv¡Â∏¿ 4 ![]() Ýn = m+4 DVg¿∞.
Ýn = m+4 DVg¿∞.
n £¿ F
®…Ø…Ai¿ƒ£¿ƒþ (1)g¿∞Ë Dz…√≤π.
m+n = 2p
m+m+4 = 2p
2m= 2p-4
m=p-2 ------ý(3)
n= m+4 Ez¿£¿ƒþ (2)
g¿∞Ë Dz…√≤π.
m(m+4) =9/4
m2+4m - 9/4 =0
I.e. (p-2)2+4(p-2) - 9/4 =0ÝÝ
{(3)g¿Av… m=p-2}
p2-4p+4 +4(p-2) - 9/4 =0 {(p-2)2 £¿ƒþ ´∏¿€jπz¡U¿ }
p2-4p+4 +4p-8 - 9/4 =0
p2-4 - 9/4 =0
p2-25/4 =0
p2= 25/4
p = ![]() Ý5/2
Ý5/2
v¡º…:
p =(-5/2) ®…Ø…Ai¿ƒ£¿ƒþ z¿v¿€ ∏¿´ƒ√P¿g¿tz¿∞Ë Dz…√≤π,
4x2-8px+9=0ÝÝ
4x2-8*(-5/2)x+9=0Ý
4x2+20x+9=0ÝÝ
F ∏¿´ƒ√P¿g¿t™¿≈ ax2+bx+c=0ÝÝ g¿∆•¿z¿∞Ëz…. Ýa=4, b=20, c=9
![]() Ýb2-4ac = 400Ý ñ 4*4*9 =
400-144 =256
Ýb2-4ac = 400Ý ñ 4*4*9 =
400-144 =256
![]() Ý
Ý![]() Ý=
Ý= ![]() (256)
= 16
(256)
= 16
∏¿∆v¿Êz¿Av…,
™¿ƒ∆ÆU¿º¿ƒ: x = [-b +![]() ]/2aÝ =(-20+16)/8Ý
=ÝÝ -4/8
]/2aÝ =(-20+16)/8Ý
=ÝÝ -4/8
ÝÝÝÝÝÝÝ x = [-b -![]() ]/2aÝÝ = (-20-16)/8 =Ý -36/8
]/2aÝÝ = (-20-16)/8 =Ý -36/8
™¿ƒ∆ÆU¿º¿ £¿q¿ƒ´£¿ ™¿Âv¡Â∏¿ 32/8 = 4 Ø…P¿Ãz¿∞Ë P…∆n÷z…ð√.
Z¿lƒ™¿nP…: p=5/2 P¿∆q¡ Ez…√ •s¿∞v¡A±¿ ßg¿ƒv¿€z…Az¿ƒ v¡º…£…∆√r.
2.19 P¿∞v¿ ™¿ƒƒS¡ÂA±¿U¿º¿ƒ
|
∏¿AS… |
£…£¿¶q¿®…√P¡z¿ CA±¿U¿º¿ƒ |
|
1 |
ax2
+bx+ c = 0 F ™¿U¿
∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¿ƒ: x = [-b+ [-b- |
|
2 |
m ™¿ƒv¿ƒ€ nU¿º¿ƒ
MAz¿ƒ ™¿U¿ ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¡z¿g…, (m+n) = -b/a |
|
3 |
m ™¿ƒv¿ƒ€ n U¿º¿ƒ
MAz¿ƒ ™¿U¿ ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¡z¿g…, (mn) = c/a |
|
4 |
m ™¿ƒv¿ƒ€ n U¿º¿ƒ MAz¿ƒ
™¿U¿ ∏¿´ƒ√P¿g¿tz¿ ™¿ƒ∆ÆU¿º¡z¿g…, x2 ñ(n+m)x +mn =0 |