6.2 ¸ÀéAiÀÄA¹zÀÞUÀ¼ÀÄ, ¹éÃPÀÈvÀ ¹zÁÞAvÀUÀ¼ÀÄ ªÀÄvÀÄÛ ºÉýPÉUÀ¼ÀÄ

(Axioms, Postulates and Enunciations on lines):

6.2.1 ¸ÀéAiÀÄA¹zÀÞUÀ¼ÀÄ(Axioms):

gÉÃSÁUÀtÂvÀzÀ°è PÉ®ªÀÅ «µÀAiÀÄUÀ¼À£ÀÄß AiÀiÁªÀÅzÉà ZÀZÉð ªÀÄvÀÄÛ ¸ÁzsÀ£ÉUÀ½®èzÉ M¦àPÉƼÀî¨ÉÃPÁUÀÄvÀÛzÉ. EªÀÅUÀ¼À£ÀÄß ‘¸ÀéAiÀÄA¹zÀÞUÀ¼ÀÄ’ ªÀÄvÀÄÛ ‘¹éÃPÀÈvÀ ¹zÁÞAvÀUÀ¼ÀÄ’ J£ÀÄßvÉÛêÉ. ¸ÀéAiÀÄA¹zÀÞ JAzÀgÉ ºÉýPÉ. F ¸ÀéAiÀÄA¹zÀÞUÀ¼ÀÄ UÀtÂvÀ ±Á¸ÀÛçzÀ EvÀgÀ «¨sÁUÀUÀ½VAvÀ gÉÃSÁUÀtÂvÀzÀ¯Éèà ºÉZÁÑV ¨ÉÃPÁUÀÄvÀÛzÉ. EªÉ¯Áè ¸ÀéAiÀÄA¤zsÀðjvÀ ¸ÀvÀå¸ÀAUÀwUÀ¼ÁVzÉ.

UÀªÀĤ¹:

1. ¸ÀéAiÀÄA¹zÀÞUÀ¼ÀÄ ¥ÀgÀ¸ÀàgÀ «gÀÄzÀÞ ºÉýPÉUÀ¼ÁUÀ¨ÁgÀzÀÄ.

2. ¸ÀéAiÀÄA¹zÀÞUÀ¼ÀÄ ¸ÀévÀAvÀæªÁVgÀ¨ÉÃPÀÄ.(MAzÀÄ ¸ÀéAiÀÄA¹zÀÞzÀ DzsÁgÀ¢AzÀ E£ÉÆßAzÀÄ ¸ÀéAiÀÄA¹zÀÞ GzÀ㫹gÀ¨ÁgÀzÀÄ)

3. ¸ÀéAiÀÄA¹zÀÞUÀ¼ÀÄ Cw PÀrªÉÄ ¸ÀASÉåAiÀÄ°ègÀ¨ÉÃPÀÄ.

1. ©ÃdUÀtÂvÀzÀ°è a = b ªÀÄvÀÄÛ b = c DzÀgÉ a = c DVgÀÄvÀÛzÉ.

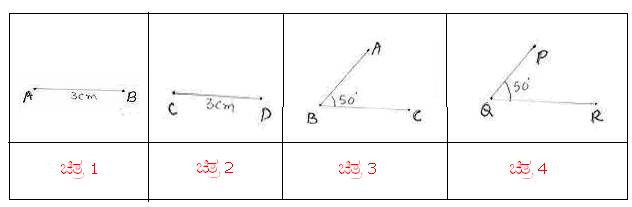
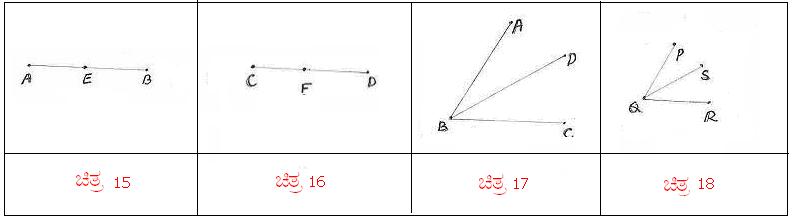
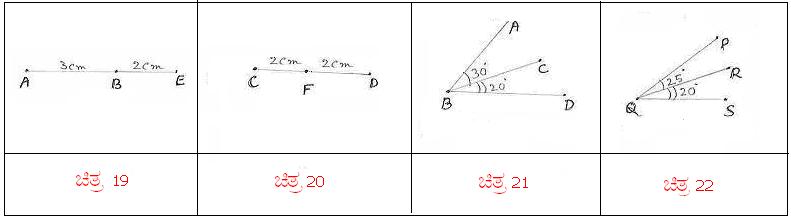
avÀæ 1 gÀ°è ABAiÀÄ GzÀÝ: 3¸ÉA.«Ä. avÀæ 2 gÀ°è CDAiÀÄ GzÀÝ 3¸ÉA.«Ä. DUÀ £ÁªÀÅ AB=CD JAzÀÄ ºÉüÀ§ºÀÄzÀÄ.	avÀæ 3 gÀ°è ABC = 50^0 avÀæ 4 gÀ°è PQR = 50^0. DUÀ ABC = PQR.
gÉÃSÁUÀtÂvÀzÀ°è F UÀÄtªÀ£ÀÄß MAzÀÄ ¸ÀéAiÀÄA¹zÀÞzÀ°è »ÃUÉ ¤gÀƦ¸À§ºÀÄzÀÄ: 6.2.1 ¸ÀéAiÀÄA¹zÀÞ1: MAzÉà CA±ÀPÉÌ ¸ÀªÀĪÁVgÀĪÀ CA±ÀUÀ¼ÀÄ ¥ÀgÀ¸ÀàgÀ ¸ÀªÀĪÁVgÀÄvÀÛªÉ.

2. ©ÃdUÀtÂvÀzÀ°è a = b DzÀgÉ a+c = b+c DVgÀÄvÀÛzÉ.

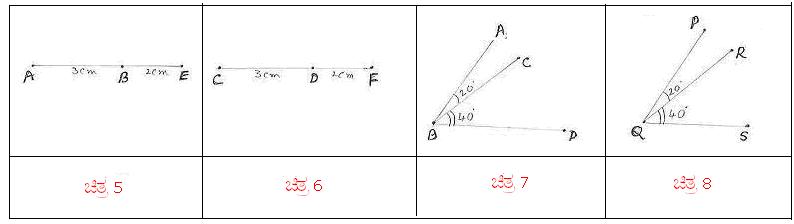
avÀæ 5 gÀ°è  AB=3¸ÉA.«Ä. BE=2¸ÉA.«Ä. avÀæ 6 gÀ°è  CD=3¸ÉA.«Ä. DF =2¸ÉA.«Ä. BE ªÀÄvÀÄÛ DFUÀ¼À£ÀÄß C£ÀÄPÀæªÀĪÁV AB ªÀÄvÀÄÛ CD UÀ½UÉ ¸ÉÃjzÁUÀ, AE=AB+BE = 5¸ÉA.«Ä.  CF=CD+DF = 5¸ÉA.«Ä. DUÀ, AE=CF.	avÀæ 7 gÀ°è ABC = 20^0, CBD = 40^0. avÀæ 8 gÀ°è PQR = 20^0, RQS = 40^0. FUÀ CBD ªÀÄvÀÄÛ RQS UÀ¼À£ÀÄß PÀæªÀĪÁV ABC ªÀÄvÀÄÛ PQR UÀ½UÉ PÀÆrzÁUÀ, ABD= 60^0 , PQS = 60^0 DUÀ, ABD =PQS.
gÉÃSÁUÀtÂvÀzÀ°è F ®PÀëtªÀ£ÀÄß MAzÀÄ ¸ÀéAiÀÄA¹zÀÞzÀ°è »ÃUÉ ºÉüÀÄvÉÛêÉ: 6.2.1 ¸ÀéAiÀÄA¹zÀÞ 2: ¥ÀgÀ¸ÀàgÀ ¸ÀªÀĪÁzÀ JgÀqÀÄ CA±ÀUÀ½UÉ, ¸ÀªÀĪÁzÀ CA±ÀUÀ¼À£ÀÄß PÀÆr¹zÁUÀ, ªÉÆvÀÛUÀ¼ÀÄ ¸ÀªÀĪÁUÀÄvÀÛªÉ.

3. ©ÃdUÀtÂvÀzÀ°è a = b DzÀgÉ a-c = b-c DVgÀÄvÀÛzÉ.

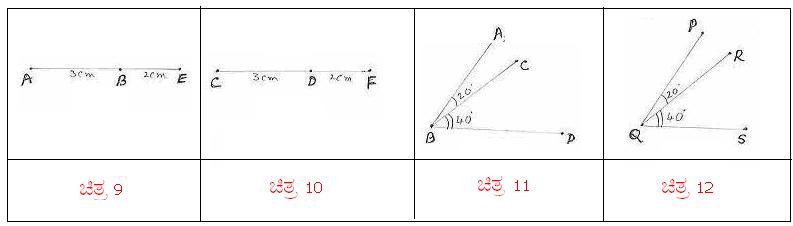
avÀæ 9 gÀ°è AE=5¸ÉA.«Ä.  BE=2¸ÉA.«Ä. avÀæ 10 gÀ°è CF=5¸ÉA.«Ä.  DF =2¸ÉA.«Ä. FUÀ BE ªÀÄvÀÄÛ DF UÀ¼À£ÀÄß PÀæªÀĪÁV AE ªÀÄvÀÄÛ CF UÀ½AzÀ PÀ¼ÉzÁUÀ, AB=AE-BE=3¸ÉA.«Ä. ªÀÄvÀÄÛ CD=CF-DF=3¸ÉA.«Ä. DUÀ  AB=CD JAzÀÄ ºÉüÀ§ºÀÄzÀÄ.	avÀæ 11 gÀ°è ABD = 60^0, CBD = 40^0. avÀæ 12 gÀ°è PQS = 60^0, RQS = 40^0. FUÀCBD ªÀÄvÀÄÛ RQS UÀ¼À£ÀÄß PÀæªÀĪÁV ABD ªÀÄvÀÄÛ PQS UÀ½AzÀ PÀ¼ÉzÁUÀ, ABC = 20^0 , PQR = 20^0 DUÀ ABC =PQR.
gÉÃSÁUÀtÂvÀzÀ°è F ®PÀëtªÀ£ÀÄß MAzÀÄ ¸ÀéAiÀÄA¹zÀÞzÀ°è »ÃUÉ ºÉüÀÄvÉÛêÉ. 6.2.1 ¸ÀéAiÀÄA¹zÀÞ 3: ¥ÀgÀ¸ÀàgÀ ¸ÀªÀĪÁzÀ JgÀqÀÄ CA±ÀUÀ½AzÀ ¸ÀªÀĪÁzÀ JgÀqÀÄ CA±ÀUÀ¼À£ÀÄß PÀ¼ÉzÁUÀ, G½AiÀÄĪÀ CA±ÀUÀ¼ÀÄ ¸ÀªÀÄ.

4. ©ÃdUÀtÂvÀzÀ°è n > 1 DzÁUÀ a > (a/n) DVgÀÄvÀÛzÉ.

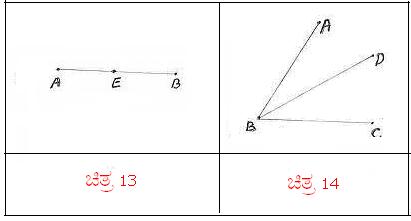
avÀæ 13 gÀ°è AB AiÀÄ£ÀÄß  AE ªÀÄvÀÄÛ EBUÀ¼ÉÆA¢UÉ ºÉÆð¹. E°è AB>AE , AB>BE.	avÀæ 14 gÀ°è ABC AiÀÄ£ÀÄß ABD ªÀÄvÀÄÛ DBCAiÉÆA¢UÉ ºÉÆð¹. ABC >ABD , ABC >DBC.
gÉÃSÁUÀtÂvÀzÀ°è F ®PÀëtªÀ£ÀÄß MAzÀÄ ¸ÀéAiÀÄA¹zÀÞzÀ°è »ÃUÉ ºÉüÀÄvÉÛêÉ. 6.2.1 ¸ÀéAiÀÄA¹zÀÞ 4: ¥ÀÇtðªÀÅ CzÀgÀ ¨sÁUÀQÌAvÀ®Æ zÉÆqÀØzÀÄ.

5. ©ÃdUÀtÂvÀzÀ°è a = b DzÀgÉ (a/2) = (b/2) DVgÀÄvÀÛzÉ.

avÀæ 15 ªÀÄvÀÄÛ 16 £Àß UÀªÀĤ¹. E°è AB=CD. E ªÀÄvÀÄÛ F UÀ¼ÀÄ PÀæªÀĪÁV AB ªÀÄvÀÄÛ CD UÀ¼À ªÀÄzsÀå©AzÀÄUÀ¼ÀÄ. DUÀ, AE=CF , EB=FD	avÀæ 17 ªÀÄvÀÄÛ 18 gÀ°è ABC = PQR.   BD ªÀÄvÀÄÛ QS UÀ¼ÀÄ PÀæªÀĪÁV ABC ªÀÄvÀÄÛ PQS UÀ¼À PÉÆãÁzsÀðPÀ gÉÃSÉUÀ¼ÀÄ. DUÀ, ABD = vPQS , DBC =SQR
F ªÉÄð£À ®PÀëtªÀ£ÀÄß MAzÀÄ ¸ÀéAiÀÄA¹zÀÞzÀ°è »ÃUÉ ºÉüÀÄvÉÛêÉ. 6.2.1 ¸ÀéAiÀÄA¹zÀÞ 5: ¥ÀgÀ¸ÀàgÀ ¸ÀªÀĪÁVgÀĪÀ CA±ÀUÀ¼À CzsÀðUÀ¼ÀÄ ¥ÀgÀ¸ÀàgÀ ¸ÀªÀÄ.

6. ©ÃdUÀtÂvÀzÀ°è a b ªÀÄvÀÄÛ c 0 DzÀgÉ (a+c) (b+c) DVgÀÄvÀÛzÉ.

avÀæ 19 ªÀÄvÀÄÛ 20 £Àß UÀªÀĤ¹. AB=3¸ÉA.«Ä. CF=2¸ÉA.«Ä. DzÀÝjAzÀ, AB CF. BE=2¸ÉA.«Ä.  FD=2¸ÉA.«Ä. AE = AB+BE=3+2=5¸ÉA.«Ä. CD=CF+FD=2+2=4¸ÉA.«Ä. DUÀ, AE CD.	avÀæ 21 ªÀÄvÀÄÛ 22 £Àß UÀªÀĤ¹ ABC =30^0, PQR= 25^0 DzÀÝjAzÀ, ABC PQR.  CBD = RQS =20^0. ABD = ABC +CBD=30^0+20^0=50^0 PQS =PQR+RQS = 25^0+20^0=45^0. DUÀ, ABD PQS.
gÉÃSÁUÀtÂvÀzÀ°è F ®PÀëtªÀ£ÀÄß MAzÀÄ ¸ÀéAiÀÄA¹zÀÞzÀ°è »ÃUÉ ºÉüÀÄvÉÛêÉ. 6.2.1 ¸ÀéAiÀÄA¹zÀÞ 6: ¥ÀgÀ¸ÀàgÀ C¸ÀªÀĪÁVgÀĪÀ CA±ÀUÀ½UÉ ¸ÀªÀÄ£ÁzÀ CA±ÀUÀ¼À£ÀÄß PÀÆr¹zÁUÀ ªÉÆvÀÛUÀ¼ÀÄ C¸ÀªÀĪÁVgÀÄvÀÛªÉ.

UÀªÀĤ¹: F ªÉÄð£À J¯Áè ¸ÀéAiÀÄA¹zÀÞUÀ¼À£ÀÄß gÉÃSÁUÀtÂvÀzÀ°è ªÀiÁvÀæªÀ®èzÉ UÀtÂvÀzÀ J¯Áè «¨sÁUÀUÀ¼À®Æè G¥ÀAiÉÆÃV¸ÀÄvÉÛêÉ.

6.2.2 DzsÁgÀ ¥ÀæweÉÕUÀ¼ÀÄ (¹éÃPÀÈvÀ ¹zÁÞAvÀUÀ¼ÀÄ)(Postulates):

ªÁåSÉå: ¸ÁªÀiÁ£Àå M¥ÀàAzÀ¢AzÀ vÉUÉzÀÄPÉÆAqÀ ‘gÉÃSÁUÀtÂvÀzÀ’ HºÁ ¸ÀvÀåUÀ¼À£ÀÄß ‘DzsÁgÀ ¥ÀæweÉÕ’ J£ÀÄߪÀgÀÄ. EªÀÅUÀ¼ÀÄ ¸ÀéAiÀÄA¹zÀÞzÀAvÉAiÉÄà DVªÉ. DzÀgÉ EªÀÅUÀ¼À ¸ÀvÁå¸ÀvÀåvÉAiÀÄ£ÀÄß ¸ÀÆPÀÛªÁzÀ gÀZÀ£É ªÀÄvÀÄÛ C¼ÀvÉUÀ½AzÀ ¥Àj²Ã°¸À§ºÀÄzÀÄ.

100 «ÄÃlgï GzÀÝzÀ NlzÀ ºÁ¢UÀ¼À£ÀÄß ºÉÃUÉ UÀÄgÀÄw¸ÀÄwÛÃgÉAzÀÄ ¤ÃªÀÅ UÀªÀĤ¹¢ÝÃgÁ? PÉ®¸ÀUÁgÀgÀÄ 100 «ÄÃlgï CAvÀgÀzÀ°è JgÀqÀÄ ©AzÀÄUÀ¼À£ÀÄß UÀÄgÀÄw¹, D JgÀqÀÄ ©AzÀÄUÀ¼À£ÀÄß ¸ÀÄtÚzÀ ¥ÀÅr G¥ÀAiÉÆÃV¹ ¸ÀgÀ¼ÀgÉÃSÉUÀ¼À£Éß¼ÉzÀÄ eÉÆÃr¸ÀÄvÁÛgÉ. E°è gÉÃSÁUÀtÂvÀzÀ AiÀiÁªÀ ¤AiÀĪÀÄUÀ¼À£ÀÄß G¥ÀAiÉÆÃV¸À¨ÉÃPÁVzÉ?
¥ÀPÀÌzÀ ¸ÀgÀ¼À gÉÃSÁ avÀæzÀ°è  A, B UÀ¼ÀÄ JgÀqÀÄ ©AzÀÄUÀ¼ÁVzÀÄÝ. AB AiÀÄÄ F JgÀqÀÄ ©AzÀÄUÀ¼À ªÀÄÆ®PÀ ºÁzÀÄ ºÉÆÃUÀĪÀ ¸ÀgÀ¼ÀgÉÃSÉAiÀiÁVzÉ.
ªÉÄð£À ®PÀëtªÀ£ÀÄß MAzÀÄ DzsÁgÀ ¥ÀæweÉÕ¬ÄAzÀ »ÃUÉ ºÉüÀ§ºÀÄzÀÄ. 6.2.2 DzsÁgÀ ¥ÀæweÉÕ1: JgÀqÀÄ ©AzÀÄUÀ¼À ªÀÄÆ®PÀ MAzÉà MAzÀÄ ¸ÀgÀ¼ÀgÉÃSÉAiÀÄ£Éß¼ÉAiÀħºÀÄzÀÄ. F DzsÁgÀ ¥ÀæweÉÕ UÉÆwÛ®èzÉAiÀÄÆ PÉ®¸ÀUÁgÀgÀÄ ºÉÃUÉ UÉgÉ J¼ÉAiÀÄÄvÁÛgÉ £ÉÆÃr!
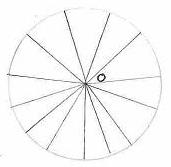
¤ÃªÀÅ ¸ÉÊPÀ°£À ZÀPÀæzÀ ªÀÄzsÀåzÀ°è PÀrØUÀ¼ÀÄ eÉÆÃr¹gÀĪÀÅzÀ£ÀÄß UÀªÀĤ¹¢ÝÃgÁ? ¥ÀPÀÌzÀ avÀæzÀ°è O ZÀPÀæzÀ ªÀÄzsÀå©AzÀÄ. ºÀ®ªÀÅ PÀrØUÀ¼À£ÀÄß PÉÃAzÀæPÉÌ eÉÆÃr¸À¯ÁVzÉ.
ªÉÄð£À ®PÀëtªÀ£ÀÄß MAzÀÄ DzsÁgÀ ¥ÀæweÉÕ¬ÄAzÀ »ÃUÉ ºÉüÀ§ºÀÄzÀÄ. 6.2.2 DzsÁgÀ ¥ÀæweÉÕ 2: MAzÀÄ ©AzÀÄ«£À ªÀÄÆ®PÀ C£ÉÃPÀ ¸ÀgÀ¼ÀgÉÃSÉUÀ¼À£ÀÄß J¼ÉAiÀħºÀÄzÀÄ.
¥ÀPÀÌzÀ avÀæzÀ°è PQ MAzÀÄ ¸ÀgÀ¼ÀgÉÃSÉAiÀiÁVzÀÄÝ CzÀ£ÀÄß JgÀqÀÆ PÀqÉUÀ½UÉ ªÀÈ¢Þ¸À¯ÁVzÉ.
ªÉÄð£À ®PÀëtªÀ£ÀÄß MAzÀÄ DzsÁgÀ ¥ÀæweÉÕ¬ÄAzÀ »ÃUÉ ºÉüÀ§ºÀÄzÀÄ. 6.2.2 DzsÁgÀ ¥ÀæweÉÕ 3: MAzÀÄ ¸ÀgÀ¼ÀgÉÃSÉAiÀÄ£ÀÄß JgÀqÀÆ PÀqÉUÀ¼À°è JµÀÄÖ zÀÆgÀPÉÌ ¨ÉÃPÁzÀgÀÆ ªÀÈ¢Þ¸À§ºÀÄzÀÄ.
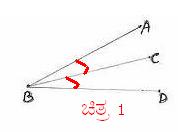
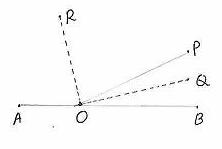
¥ÀPÀÌzÀ avÀæzÀ°è O ©AzÀÄ«¤AzÀ  OA ªÀÄvÀÄÛ OB gÉÃSÁQgÀtUÀ¼À£ÀÄß ¥ÀgÀ¸ÀàgÀ «gÀÄzÀÞ ¢QÌ£À°è J¼ÉAiÀįÁVzÉ. O ©AzÀÄ«£À°è DzÀ PÉÆãÀªÀ£ÀÄß C¼É¬Äj AOB = 180^0
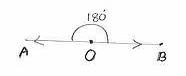
ªÉÄð£À ®PÀëtªÀ£ÀÄß MAzÀÄ DzsÁgÀ ¥ÀæweÉÕ¬ÄAzÀ »ÃUÉ ºÉüÀ§ºÀÄzÀÄ. 6.2.2 DzsÁgÀ ¥ÀæweÉÕ 4: MAzÀPÉÆÌAzÀÄ «gÀÄzÀÞ ¢QÌ£À°ègÀĪÀ JgÀqÀÄ QgÀtUÀ¼À DgÀA¨sÀzÀ ©AzÀÄ«£À°è K¥ÀðqÀĪÀ PÉÆãÀªÀÅ 180^0 EgÀÄvÀÛzÉ.
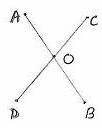
¤ÃªÀÅ PÀÄaðAiÀÄ°è ºÉÃUÉ PÀĽvÀÄPÉƼÀÄî«j? PÁ®ÄUÀ¼À£ÀÄß ¥ÀgÀ¸ÀàgÀ bÉâ¸ÀĪÀAvÉ ºÁQ CxÀªÁ PÁ®ÄUÀ¼À£ÀÄß MAzÀPÉÆÌAzÀÄ ¸ÀªÀiÁ£ÁAvÀgÀªÁVlÄÖPÉÆAqÀÄ ... ¥ÀPÀÌzÀ avÀæzÀ°è  AB ªÀÄvÀÄÛ CD gÉÃSÉUÀ¼ÀÄ O ©AzÀÄ«£À°è bÉâ¸ÀÄvÀÛzÉ CxÀªÁ CªÀÅUÀ¼ÀÄ ¥ÀgÀ¸ÀàgÀ ¸ÀªÀiÁ£ÁAvÀgÀªÁVªÉ.
ªÉÄð£À ®PÀëtªÀ£ÀÄß MAzÀÄ DzsÁgÀ ¥ÀæweÉÕ¬ÄAzÀ »ÃUÉ ºÉüÀ§ºÀÄzÀÄ. 6.2.2 DzsÁgÀ ¥ÀæweÉÕ 5: JgÀqÀÄ ¸ÀgÀ¼ÀgÉÃSÉUÀ¼ÀÄ MAzÉà MAzÀÄ G¨sÀAiÀÄ ¸ÁªÀiÁ£Àå ©AzÀĪÀ£ÀÄß ºÉÆA¢gÀÄvÀÛzÉ CxÀªÁ AiÀiÁªÀÅzÉà ¸ÁªÀiÁ£Àå ©AzÀÄ ºÉÆA¢gÀĪÀÅ¢®è.
gÉʯÉéà ºÀ½UÀ¼ÀÄ ¥ÀgÀ¸ÀàgÀ ¸ÀA¢ü¹zÀgÉãÁUÀÄvÀÛzÉ? gÉʯÉéà ¥ÀæAiÀiÁt C¸ÁzsÀå… ¥ÀPÀÌzÀ avÀæzÀ°è AB ªÀÄvÀÄÛ CD ¸ÀgÀ¼ÀgÉÃSÉUÀ¼ÀÄ ¸ÀªÀiÁ£ÁAvÀgÀªÁVzÀÄÝ, CªÀÅUÀ¼À£ÀÄß JgÀqÀÆ §¢UÀ¼À°è JµÀÄÖ zÀÆgÀPÉÌ ªÀÈ¢Þ¹zÀgÀÆ ¸ÀA¢ü¸ÀĪÀÅ¢®è. (gÉʯÉéà ºÀ½AiÀÄAvÉ)
ªÉÄð£À ®PÀëtªÀ£ÀÄß MAzÀÄ DzsÁgÀ ¥ÀæweÉÕ¬ÄAzÀ »ÃUÉ ºÉüÀ§ºÀÄzÀÄ. 6.2.2 DzsÁgÀ ¥ÀæweÉÕ 6: JgÀqÀÄ ¸ÀªÀiÁ£ÁAvÀgÀ ¸ÀgÀ¼ÀgÉÃSÉUÀ¼À£ÀÄß C£ÀAvÀ zÀÆgÀzÀªÀgÉUÉ ªÀÈ¢Þ¹zÀgÀÆ CªÀÅ ¥ÀgÀ¸ÀàgÀ ¸ÀA¢ü¸ÀĪÀÅ¢®è.

wêÀiÁð£À: DzsÁgÀ ¥ÀæweÉÕ 5 ªÀÄvÀÄÛ 6jAzÀ, £ÁªÉãÀÄ wêÀiÁð£ÀPÉÌ §gÀ§ºÀÄzÀÄ? JgÀqÀÄ ¸ÀgÀ¼ÀgÉÃSÉUÀ¼ÀÄ MAzÀÄ ¸ÁªÀiÁ£Àå ©AzÀĪÀ£ÀÄß ºÉÆA¢gÀ¢zÀÝgÉ, CªÀÅUÀ¼ÀÄ ¸ÀªÀiÁ£ÁAvÀgÀ ¸ÀgÀ¼ÀgÉÃSÉUÀ¼ÁVgÀÄvÀÛªÉ.

6.2.3 ºÉýPÉUÀ¼ÀÄ(Enunciations):

gÉÃSÁUÀtÂvÀzÀ°è PÉ®ªÀÅ ¸ÀvÀå ¸ÀAUÀwUÀ¼ÀÄ ºÉýPÉAiÀÄ gÀÆ¥ÀzÀ°ègÀÄvÀÛªÉ. F ºÉýPÉUÀ¼À ¸ÀvÁåA±ÀªÀ£ÀÄß gÀZÀ£É ªÀÄvÀÄÛ C¼ÀvÉUÀ½AzÀ w½AiÀħºÀÄzÀÄ.

¥ÀPÀÌzÀ avÀæzÀ°è AOC + COB = 180^0
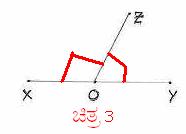
ªÉÄð£À ¸ÀvÁåA±ÀªÀ£ÀÄß PɼÀV£À ºÉýPÉ gÀÆ¥ÀzÀ°è §gÉAiÀħºÀÄzÀÄ. 6.2.3 ºÉýPÉ1: MAzÀÄ ¸ÀgÀ¼ÀgÉÃSÉAiÀÄ ªÉÄÃ¯É MAzÀÄ gÉÃSÁQgÀt ¤AvÁUÀ D ¸ÁªÀiÁ£Àå ©AzÀÄ«£À°è GAmÁUÀĪÀ PÉÆãÀUÀ¼À ªÉÆvÀÛ 180^0EgÀÄvÀÛzÉ. D PÉÆãÀUÀ¼À£ÀÄß ¸ÀgÀ¼ÀAiÀÄÄUÀä PÉÆãÀUÀ¼ÀÄ J£ÀÄßvÉÛêÉ. EzÀ£ÀÄß PÉ®ªÀÅ ¨Áj ‘¸ÀgÀ¼ÀAiÀÄÄUÀä ¸ÀéAiÀÄA¹zÀÞ’ (Linear pair axiom) J£ÀÄߪÀgÀÄ.
¥ÀPÀÌzÀ avÀæzÀ°è AB ªÀÄvÀÄÛ CD gÉÃSÉUÀ¼ÀÄ O ©AzÀÄ«£À°è bÉâ¸ÀÄvÀÛªÉ. DUÀ, AOC = DOB ªÀÄvÀÄÛ AOD = COB
ªÉÄð£À ¸ÀvÁåA±ÀªÀ£ÀÄß PɼÀV£À ºÉýPÉ gÀÆ¥ÀzÀ°è §gÉAiÀħºÀÄzÀÄ. 6.2.3 ºÉýPÉ 2: JgÀqÀÄ ¸ÀgÀ¼ÀgÉÃSÉUÀ¼ÀÄ ¥ÀgÀ¸ÀàgÀ bÉâ¹zÁUÀ GAmÁUÀĪÀ ±ÀÈAUÁ©üªÀÄÄR PÉÆãÀUÀ¼ÀÄ ¸ÀªÀÄ. EzÀPÉÌ GzÁºÀgÀuÉ PÀvÀÛj.

ªÉÄð£À ºÉýPÉAiÀÄ£ÀÄß F PɼÀV£ÀAvÉ ¸Á¢ü¸À§ºÀÄzÀÄ:

¸ÀA.	¤gÀÆ¥ÀuÉ	PÁgÀtUÀ¼ÀÄ
1	AOC + COB = 180^0	DzsÁgÀ ¥ÀæweÉÕ 1: ABAiÀÄÄ MAzÀÄ ¸ÀgÀ¼ÀgÉÃSÉ OC AiÀÄÄ AB ªÉÄÃ¯É ¤AwzÉ.
2	DOA + AOC = 180^0	DzsÁgÀ ¥ÀæweÉÕ  1: DCAiÀÄÄ MAzÀÄ ¸ÀgÀ¼ÀgÉÃSÉ OAAiÀÄÄ  DC ªÉÄÃ¯É ¤AwzÉ.
3	AOC + COB =DOA + AOC	¸ÀéAiÀÄA¹zÀÞ 1
4	COB = DOA	¸ÀéAiÀÄA¹zÀÞ 3(AOC AiÀÄ£ÀÄß JgÀqÀÆ §¢UÀ½AzÀ PÀ¼É¢zÉ)

EzÉà jÃwAiÀiÁV, AOC = DOB JAzÀÄ ¸Á¢ü¸À§ºÀÄzÀÄ.

ªÁåSÉåUÀ¼ÀÄ:

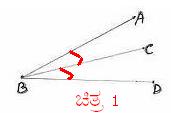
1.AiÀiÁªÀÅzÉà JgÀqÀÄ PÉÆãÀUÀ¼ÀÄ G¨sÀAiÀÄ ¸ÁªÀiÁ£Àå ¨ÁºÀÄ MAzÀÄ G¨sÀAiÀÄ ¸ÁªÀiÁ£Àå ±ÀÈAUÀ ©AzÀĪÀ£ÀÄß ºÉÆA¢zÀÝgÉ, CAvÀºÀ PÉÆãÀUÀ¼À£ÀÄß ‘¥Á±Àéð PÉÆãÀUÀ¼ÀÄ’ (adjacent) J£ÀÄßvÉÛêÉ. ¥ÀPÀÌzÀ avÀæ 1 gÀ°è ABC ªÀÄvÀÄÛ CBD UÀ¼ÀÄ ¥Á±Àéð PÉÆãÀUÀ¼ÀÄ E°è BAiÀÄÄ ¸ÁªÀiÁ£Àå ©AzÀÄ. BCAiÀÄÄ ¸ÁªÀiÁ£Àå ¨ÁºÀÄ
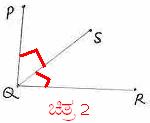
2. JgÀqÀÄ PÉÆãÀUÀ¼À ªÉÆvÀÛ 90^0EzÀÝgÉ, D JgÀqÀÄ PÉÆãÀUÀ¼À£ÀÄß “¥ÀÇgÀPÀ PÉÆãÀUÀ¼ÀÄ”(complimentary) J£ÀÄßvÉÛêÉ. ¥ÀPÀÌzÀ avÀæ 2 gÀ°è PQS +SQR = PQR ªÀÄvÀÄÛ PQR=90^0 DzÀÝjAzÀ PQS ªÀÄvÀÄÛ SQR UÀ¼ÀÄ ¥ÀÇgÀPÀPÉÆãÀUÀ¼ÀÄ
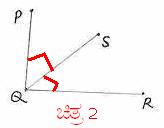
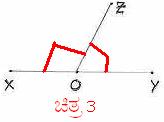
3. JgÀqÀÄ PÉÆãÀUÀ¼À ªÉÆvÀÛ 180^0EzÀÝgÉ, D JgÀqÀÄ PÉÆãÀUÀ¼À£ÀÄß “¥Àj¥ÀÇgÀPÀ PÉÆãÀUÀ¼ÀÄ” (CxÀªÁ ¸ÀA¥ÀÇgÀPÀ PÉÆãÀUÀ¼ÀÄ)(supplementary) J£ÀÄßvÉÛêÉ. ¥ÀPÀÌzÀ avÀæ 3 gÀ°è XOZ ªÀÄvÀÄÛ ZOY UÀ¼ÀÄ ¥Àj¥ÀÇgÀPÀ PÉÆãÀUÀ¼ÀÄ. KPÉAzÀgÉ XOZ+XOY = 180^0)

¸ÀA	PÉÆãÀUÀ¼À «AUÀqÀuÉ	GzÁºÀgÀuÉ
1	¥Á±Àéð PÉÆãÀUÀ¼ÀÄ	ABC ªÀÄvÀÄÛ CBD
2	¥ÀÇgÀPÀ PÉÆãÀUÀ¼ÀÄ	PQS ªÀÄvÀÄÛ SQR PQS +SQR=90^0
3	¥Àj¥ÀÇgÀPÀ PÉÆãÀUÀ¼ÀÄ	XOZ ªÀÄvÀÄÛ XOY XOZ +XOY=180^0

4

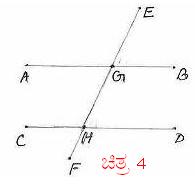
MAzÉà ¸ÀªÀÄvÀ®zÀ°ègÀĪÀ JgÀqÀÄ ¸ÀgÀ¼À gÉÃSÉUÀ¼À£ÀÄß ¨ÉÃgÉ ¨ÉÃgÉ ©AzÀÄUÀ¼À°è bÉâ¸ÀĪÀ gÉÃSÉAiÀÄ£ÀÄß ‘bÉÃzÀPÀ gÉÃSÉ’(transversal) J£ÀÄߪÀgÀÄ. ¥ÀPÀÌzÀ avÀæ 4 gÀ°è  AB ªÀÄvÀÄÛ CD UÀ¼ÀÄ MAzÉà ¸ÀªÀÄvÀ®zÀ°è£À JgÀqÀÄ ¸ÀgÀ¼À gÉÃSÉUÀ¼ÀÄ. EF gÉÃSÉAiÀÄÄ ABAiÀÄ£ÀÄß GAiÀÄ°èAiÀÄÆ CDAiÀÄ£ÀÄß H AiÀÄ°èAiÀÄÆ bÉâ¸ÀÄvÀÛªÉ. DzÀÝjAzÀ EF MAzÀÄ bÉÃzÀPÀgÉÃSÉ.

JgÀqÀÄ ¸ÀgÀ¼À gÉÃSÉUÀ¼À£ÀÄß MAzÀÄ bÉÃzÀPÀ gÉÃSÉAiÀÄÄ bÉâ¹zÁUÀ GAmÁUÀĪÀ ««zsÀ PÉÆãÀUÀ¼ÀÄ:

¥Á±Àéð PÉÆãÀUÀ¼ÀÄ	±ÀÈAUÁ©üªÀÄÄR PÉÆãÀUÀ¼ÀÄ (4 eÉÆvÉ)	¥ÀAiÀiÁðAiÀÄ PÉÆãÀUÀ¼ÀÄ (2 eÉÆvÉ)	C£ÀÄgÀÆ¥À PÉÆãÀUÀ¼ÀÄ (4 eÉÆvÉ)	CAvÀgï PÉÆãÀUÀ¼ÀÄ (2 eÉÆvÉ)
AGE & EGB	AGE & HGB	AGH & GHD	EGB & GHD	AGH and GHC
CHF &FHD	CHF & GHD	BGH & CHG	AGE & CHG	BGH and GHD
…….	AGH &EGB		AGH & CHF
	CHG &FHD		BGH & DHF

¥ÀPÀÌzÀ avÀæzÀ°è  AB ªÀÄvÀÄÛ CD UÀ¼ÀÄ ¸ÀªÀiÁAvÀgÀ ¸ÀgÀ¼ÀgÉÃSÉUÀ¼ÀÄ. EF bÉÃzÀPÀ gÉÃSÉ. DUÀ, EGB = GHD AGH = CHF AGE =CHG ªÀÄvÀÄÛ BGH = DHF.
ªÉÄð£À ¸ÀvÁåA±ÀªÀ£ÀÄß PɼÀV£À ºÉýPÉ gÀÆ¥ÀzÀ°è §gÉAiÀħºÀÄzÀÄ. 6.2.3 ºÉýPÉ 3: MAzÀÄ bÉÃzÀPÀ gÉÃSÉAiÀÄÄ JgÀqÀÄ ¸ÀªÀiÁAvÀgÀ ¸ÀgÀ¼ÀgÉÃSÉUÀ¼À£ÀÄß bÉâ¹zÁUÀ GAmÁUÀĪÀ C£ÀÄgÀÆ¥ÀPÉÆãÀUÀ¼ÀÄ ¸ÀªÀĪÁVgÀÄvÀÛzÉ.

6.2.3 ºÉýPÉ 4: MAzÀÄ eÉÆvÉ C£ÀÄgÀÆ¥ÀPÉÆãÀUÀ¼ÀÄ ¸ÀªÀĪÁVgÀĪÀAvÉ MAzÀÄ bÉÃzÀPÀ gÉÃSÉAiÀÄÄ JgÀqÀÄ ¸ÀgÀ¼ÀgÉÃSÉUÀ¼À£ÀÄß PÀvÀÛj¹zÀgÉ, D JgÀqÀÄ gÉÃSÉUÀ¼ÀÄ ¸ÀªÀiÁAvÀgÀ gÉÃSÉUÀ¼ÁVgÀÄvÀÛªÉ. (EzÀÄ ºÉýPÉ 6.2.3.3 gÀ «¯ÉÆêÀÄ)

6.2 ¸ÀªÀĸÉå  1 : avÀæzÀ°è O JA§ÄzÀÄ AB ¸ÀgÀ¼À gÉÃSÉAiÀÄ ªÉÄð£À MAzÀÄ ©AzÀÄ. OP gÉÃSÁQgÀtªÀÅABAiÀÄ ªÉÄÃ¯É O©AzÀÄ«£À°è ¤AwzÉ.

OQ gÉÃSÉAiÀÄÄ POB AiÀÄ£ÀÄß, OR gÉÃSÉAiÀÄÄ AOPAiÀÄ£ÀÄß C¢üð¸ÀÄvÀÛªÉ. DUÀ ROQ = 90⁰ JAzÀÄ ¸Á¢ü¹.

¥ÀjºÁgÀ:

¸ÀA.	¤gÀÆ¥ÀuÉ	PÁgÀtUÀ¼ÀÄ
1	POQ = QOB	OQ ªÀÅ POBAiÀÄ PÉÆãÁzsÀð gÉÃSÉ.
2	POB  = 2* POQ	ºÀAvÀ 1jAzÀ
3	AOP = 2*ROP	OR ªÀÅ AOP AiÀÄ PÉÆãÁzsÀð gÉÃSÉ.
4	AOP + POB = 180^0	ºÉýPÉ 1: AB gÉÃSÉAiÀÄ ªÉÄÃ¯É QgÀt OP ¤AwzÉ.
5	2* ROP +2*POQ =180^0	ºÀAvÀ  4,2,3 jAzÀ
6	2(ROP +POQ) =180^0	¸ÀÄ®©üÃPÀj¹
7	ROP +POQ =90^0
8	ROQ=90^0	ROP +POQ=ROQ

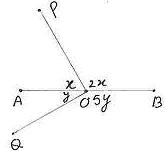
6.2 ¸ÀªÀĸÉå 2: avÀæzÀ°è O JA§ÄzÀÄ AB AiÀÄ ªÉÄð£À MAzÀÄ ©AzÀÄ. OP ªÀÄvÀÄÛ OQ QgÀtUÀ¼ÀÄ AB AiÀÄ ªÉÄÃ¯É O©AzÀÄ«£À°è ¤AwªÉ. C°è GAmÁzÀ PÉÆãÀUÀ¼À£ÀÄß

PÀAqÀÄ»rzÀÄ QOPAiÀÄÄ MAzÀÄ ®A§PÉÆãÀ JAzÀÄ vÉÆÃj¹.

¥ÀjºÁgÀ:

¸ÀA.	¤gÀÆ¥ÀuÉ	PÁgÀtUÀ¼ÀÄ
1	AOP+POB=180^0	ºÉýPÉ1:  ABAiÀÄ ªÉÄÃ¯É OP ¤AwzÉ.
2	x+2x = 180^0 i.e.3x =180^0 i.e.  x =60^0
3	AOQ+QOB=180^0	ºÉýPÉ 1: ABAiÀÄ ªÉÄÃ¯É OQ ¤AwzÉ.
4	y+5y = 180^0 i.e.  6y = 180^0 i.e.  y =30^0
5	AOP = x = 60^0POB = 2x = 120^0
6	AOQ = y =  30^0,QOB = 5y =150^0
7	QOP = QOA +AOP= y+x =30^0+ 60^0= 90^0

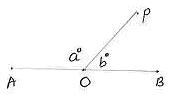
6.2 ¸ÀªÀĸÉå  3: avÀæzÀ°è AB gÉÃSÉAiÀÄ ªÉÄð£À ©AzÀÄ ‘O’. a-b=80⁰ DzÀgÉ a ªÀÄvÀÄÛ b UÀ¼À£ÀÄß PÀAqÀÄ»r.

¥ÀjºÁgÀ:

¸ÀA.	¤gÀÆ¥ÀuÉ	PÁgÀtUÀ¼ÀÄ
1	AOP+POB=180^0	ºÉýPÉ  1: ABAiÀÄ ªÉÄÃ¯É OP ¤AwzÉ.
2	a+b= 180^0	DzÉò¹zÉ.
3	b = 180^0-a
4	a-b = 80^0
5	a-b= a – (180^0 -a) = 2a -180^0
6	2a -180^0=80^0	a-b =80 zÀvÀÛ
7	2a =80^0+180^0= 260^0: 2a =260^0
8	a= 130^0:b =50^0

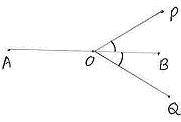
6.2 ¸ÀªÀĸÉå  4: avÀæzÀ°è OBAiÀÄÄ POQªÀ£ÀÄß C¢üð¸ÀÄvÀÛzÉ. OA ªÀÄvÀÄÛ OBUÀ¼ÀÄ «gÀÄzÀÞ ¢QÌ£À°ègÀĪÀ QgÀtUÀ¼ÀÄ

AOP = AOQ JAzÀÄ ¸Á¢ü¹.

¥ÀjºÁgÀ:

¸ÀA.	¤gÀÆ¥ÀuÉ	PÁgÀtUÀ¼ÀÄ
1	AOP+POB=180^0	¸ÀgÀ¼ÀAiÀÄÄUÀä PÉÆãÀUÀ¼ÀÄ
2	AOP = 180^0-POB
3	POB = BOQ	OBAiÀÄÄ POQªÀ£ÀÄß C¢üð¸ÀÄvÀÛzÉ.
4	AOP = 180^0-BOQ	3£Àß 2gÀ°è DzÉò¹zÉ.
5	AOQ+QOB=180^0	ºÉýPÉ 1: ¸ÀgÀ¼ÀAiÀÄÄUÀä PÉÆãÀUÀ¼ÀÄ
6	AOQ = 180^0-BOQ
7	AOP = 180^0-BOQ=  AOQ	4 ªÀÄvÀÄÛ  6jAzÀ

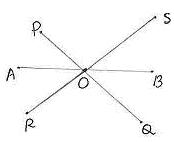
6.2 ¸ÀªÀĸÉå  5: avÀæzÀ°è PQ ªÀÄvÀÄÛ RS gÉÃSÉUÀ¼ÀÄ O£À °è bÉâ¸ÀÄwÛªÉ. OAAiÀÄÄ POR£Àß C¢üð¸ÀÄvÀÛzÉ. OBAiÀÄÄ SOQ£Àß C¢üð¸ÀÄvÀÛzÉ.

AB ¸ÀgÀ¼À gÉÃSÉ JAzÀÄ vÉÆÃj¹.

¥ÀjºÁgÀ:

¸ÀA.	¤gÀÆ¥ÀuÉ	PÁgÀtUÀ¼ÀÄ
1	POR = 2AOP	OAAiÀÄÄ POR£Àß C¢üð¸ÀÄvÀÛzÉ.
2	SOQ = 2BOQ	OBAiÀÄÄ SOQ£Àß C¢üð¸ÀÄvÀÛzÉ.
3	POR = SOQ	±ÀÈAUÁ©üªÀÄÄR PÉÆãÀUÀ¼ÀÄ ¥ÀgÀ¸ÀàgÀ ¸ÀªÀÄ.
4	2AOP = 2BOQ: AOP =BOQ
5	AOB = AOP+POS+SOB
6	= BOQ+POS+SOB	AOPUÉBOQªÀ£ÀÄß DzÉò¹zÉ.
7	=POS+SOB+BOQ
8	= 180^0	PQ MAzÀÄ ¸ÀgÀ¼ÀgÉÃSÉ. OS JA§ÄzÀÄ CzÀgÀ ªÉÄð£À QgÀt SOQ =SOB+BOQ. AB AiÀÄÄ MAzÀÄ ¸ÀgÀ¼ÀgÉÃSÉ.

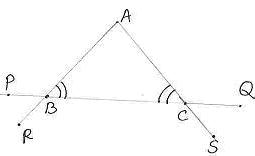
6.2  ¸ÀªÀĸÉå  6: avÀæzÀ°è ABC = ACB DzÀgÉ ACQ =ABP ªÀÄvÀÄÛCBR =BCS JAzÀÄ vÉÆÃj¹.

¥ÀjºÁgÀ:

¸ÀA.	¤gÀÆ¥ÀuÉ	PÁgÀtUÀ¼ÀÄ
1	ACB+ACQ = 180^0	BCAiÀÄÄ MAzÀÄ ¸ÀgÀ¼ÀgÉÃSÉ.
2	ACB = 180^0 – ACQ
3	PBA+ABC = 180^0	BCAiÀÄÄ MAzÀÄ ¸ÀgÀ¼ÀgÉÃSÉ.
4	PBA = 180^0 – ABC
5	= 180^0 – ACB
6	= 180^0 – (180^0 –ACQ)	2gÀ°è ACB =180^0-ACQ
7	= ACQ
8	PBR=ABC	±ÀÈAUÁ©üªÀÄÄR PÉÆãÀUÀ¼ÀÄ
9	QCS=ACB	±ÀÈAUÁ©üªÀÄÄR PÉÆãÀUÀ¼ÀÄ
10	PBR = QCS	8,9  ªÀÄvÀÄÛ  zÀvÀÛ ABC=ACB
11	CBR = 180^0 – PBR	CBR +PBR = 180^0
12	= 180^0 – QCS	10
13	=180^0 – (180^0 – BCS)	QCS+BCS = 180^0
14	= BCS

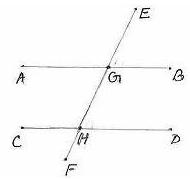
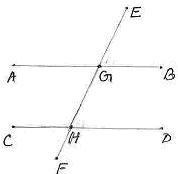
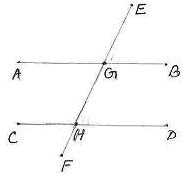
6.2  ¸ÀªÀĸÉå  7: avÀæzÀ°è AGE=120⁰. CHF = 60⁰. AB ªÀÄvÀÄÛ CD UÀ¼ÀÄ ¸ÀªÀiÁ£ÁAvÀgÀªÁVªÉAiÉÄà JAzÀÄ ¥ÀjÃQë¹

¥ÀjºÁgÀ:

¸ÀA.	¤gÀÆ¥ÀuÉ	PÁgÀtUÀ¼ÀÄ
1	CHF = GHD = 60^0	CHF ªÀÄvÀÄÛ GHD UÀ¼ÀÄ ±ÀÈAUÁ©üªÀÄÄR PÉÆãÀUÀ¼ÀÄ CHF = 60^0(zÀvÀÛ)
2	EGB = 60^0.	AGE = 120^0, AGE + EGB =180^0 ¸ÀgÀ¼ÀAiÀÄÄUÀäUÀ¼ÀÄ.
3	EGB = GHD	1 ªÀÄvÀÄÛ 2jAzÀ.

EGB ªÀÄvÀÄÛ GHD UÀ¼ÀÄ C£ÀÄgÀÆ¥À PÉÆãÀUÀ¼ÀÄ. ºÉýPÉ 4gÀAvÉ, C£ÀÄgÀÆ¥À PÉÆãÀUÀ¼ÀÄ ¸ÀªÀĪÁzÀÝjAzÀ, AB ªÀÄvÀÄÛ CDUÀ¼ÀÄ ¸ÀªÀiÁ£ÁAvÀgÀ.

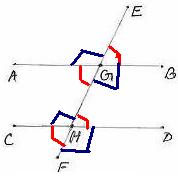
6.2 ¸ÀªÀĸÉå  8: avÀæzÀ°è  AB||CD, EF bÉÃzÀPÀªÀÅ CªÀÅUÀ¼À£ÀÄß PÀæªÀĪÁV G ªÀÄvÀÄÛ HUÀ¼À°è bÉâ¹zÉ. AGE ªÀÄvÀÄÛ EGBUÀ¼ÀÄ 3:2 C£ÀÄ¥ÁvÀzÀ°èzÀÝgÉ,

avÀæzÀ°è J¯Áè PÉÆãÀUÀ¼À£ÀÄß PÀAqÀÄ»r¬Äj.

¥ÀjºÁgÀ:

ABAiÀÄÄ MAzÀÄ ¸ÀgÀ¼ÀgÉÃSÉ. DzÀÝjAzÀ AGE + EGB =180⁰.

F PÉÆãÀUÀ¼À C£ÀÄ¥ÁvÀ 3:2. DzÀÝjAzÀ  180⁰AiÀÄ£Àß F C£ÀÄ¥ÁvÀPÀÌ£ÀÄUÀÄtªÁV «¨sÁV¸À¨ÉÃPÀÄ.

C£ÀÄ¥ÁvÀzÀ ¥ÀjªÀiÁtUÀ¼À ªÉÆvÀÛ = 3+2 =5:

5 ¥ÀjªÀiÁtzÀ ¨É¯É = 180⁰

1 ¥ÀjªÀiÁtzÀ ¨É¯É = 180⁰÷5 = 36⁰

AGE = 3 ¥ÀjªÀiÁt = 3*36⁰ = 108⁰

EGB = 2 ¥ÀjªÀiÁt = 2*36⁰ = 72⁰

¤gÀÆ¥ÀuÉ	PÁgÀtUÀ¼ÀÄ
AGE = HGB =108^0	±ÀÈAUÁ©üªÀÄÄR PÉÆãÀUÀ¼ÀÄ
EGB = AGH = 72^0	±ÀÈAUÁ©üªÀÄÄR PÉÆãÀUÀ¼ÀÄ
EGB = GHD = 72^0	C£ÀÄgÀÆ¥À PÉÆãÀUÀ¼ÀÄ
AGE = CHG =108^0	C£ÀÄgÀÆ¥À PÉÆãÀUÀ¼ÀÄ
DHF = CHG =108^0	±ÀÈAUÁ©üªÀÄÄR PÉÆãÀUÀ¼ÀÄ
CHF = GHD = 72^0	±ÀÈAUÁ©üªÀÄÄR PÉÆãÀUÀ¼ÀÄ

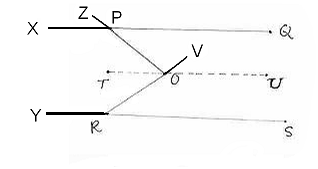
6.2 ¸ÀªÀĸÉå  9: avÀæzÀ°è  PQ||RS. DzÀgÉ QPO + ORS = POR JAzÀÄ ¸Á¢ü¹.

gÀZÀ£É: PQ UÉ ¸ÀªÀiÁAvÀgÀªÁV O ©AzÀÄ«£À ªÀÄÆ®PÀ TU ¸ÀgÀ¼ÀgÉÃSÉ J¼É¬Äj.

SR£Àß YªÀgÉUÉ, QPAiÀÄ£ÀÄß XªÀgÉUÉ, ROªÀ£ÀÄß VªÀgÉUÉ, OPAiÀÄ£ÀÄß ZªÀgÉUÉ ªÀÈ¢Þ¹.

¸ÀA.	¤gÀÆ¥ÀuÉ	PÁgÀtUÀ¼ÀÄ
1	TOP= XPZ	(XQ||TU) C£ÀÄgÀÆ¥À PÉÆãÀUÀ¼ÀÄ
2	XPZ=QPO	±ÀÈAUÁ©üªÀÄÄR PÉÆãÀUÀ¼ÀÄ
3	QPO= TOP	1 ªÀÄvÀÄÛ 2jAzÀ.
4	ROT = VOU	±ÀÈAUÁ©üªÀÄÄR PÉÆãÀUÀ¼ÀÄ
5	VOU = 180^0-TOV	TOU MAzÀÄ ¸ÀgÀ¼ÀgÉÃSÉ
6	TOV = YRV	(TU||YS) C£ÀÄgÀÆ¥À PÉÆãÀUÀ¼ÀÄ
7	VOU = 180^0-YRV	5 ªÀÄvÀÄÛ 6jAzÀ.
8	180^0-YRV = ORS	YS MAzÀÄ ¸ÀgÀ¼ÀgÉÃSÉ
9	VOU =ORS	7 ªÀÄvÀÄÛ 8jAzÀ.
10	ROT = ORS	4 ªÀÄvÀÄÛ 9jAzÀ.
11	POR = POT +TOR = QPO+ORS	3 ªÀÄvÀÄÛ 10jAzÀ.

6.2 PÀ°vÀ ªÀÄÄSÁåA±ÀUÀ¼ÀÄ

¸ÀASÉå	PÀ°vÀ CA±ÀUÀ¼ÀÄ
1	¸ÀéAiÀÄA¹zÀÞUÀ¼ÀÄ, DzsÁgÀ ¥ÀæweÉÕUÀ¼ÀÄ ªÀÄvÀÄÛ ºÉýPÉUÀ¼ÀÄ.