6.7 ZÀvÀĨsÀÄðdUÀ¼ÀÄ    (Quadrilateral):

6.7.1 Properties of Quadrilaterals

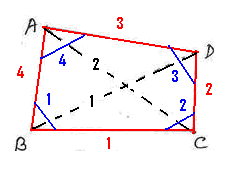
ªÁåSÉå: MAzÀÄ ¸ÀªÀÄvÀ®zÀ°è £Á®ÄÌ gÉÃSÁ RAqÀUÀ½AzÀ ¸ÀÄvÀÄÛªÀjAiÀÄ®àlÖ DPÀÈwAiÉÄà ‘ZÀvÀĨsÀÄðd’ (quadrilateral).

®PÀëëtUÀ¼ÀÄ:

4 ±ÀÈAUÀUÀ¼ÀÄ	4 ¨ÁºÀÄUÀ¼ÀÄ	4 PÉÆãÀUÀ¼ÀÄ	2 PÀtðUÀ¼ÀÄ
A, B, C, D	BC, CD,DA,AB	ABC, BCD, CDA, DAB	BD,AC

¥Àæwà PÀtðªÀÇ ZÀvÀĨsÀÄðdªÀ£ÀÄß 2 wæPÉÆãÀUÀ¼ÁV «¨sÁV¸ÀÄvÀÛzÉ.

(BAC ªÀÄvÀÄÛ ADC UÀ¼À°è AC ¸ÁªÀiÁ£Àå ¥ÁzÀ).

(BAD ªÀÄvÀÄÛ BDC UÀ¼À°è BD ¸ÁªÀiÁ£Àå ¥ÁzÀ).

EvÀgÀ ¥ÀzÀUÀ¼ÀÄ	®PÀëëtUÀ¼ÀÄ:
¥Á±Àðé (adjacent) ¨ÁºÀÄUÀ¼ÀÄ	MAzÀÄ ¸ÁªÀiÁ£Àå ±ÀÈAUÀ ©AzÀĪÀ£ÀÄß ºÉÆA¢gÀĪÀ JgÀqÀÄ ¨ÁºÀÄUÀ¼ÀÄ
C©üªÀÄÄR (opposite) ¨ÁºÀÄUÀ¼ÀÄ	MAzÀÄ ¸ÁªÀiÁ£Àå ±ÀÈAUÀ ©AzÀĪÀ£ÀÄß ºÉÆA¢®èzÀ JgÀqÀÄ ¨ÁºÀÄUÀ¼ÀÄ
C£ÀÄPÀæªÀÄ (adjacent) PÉÆãÀUÀ¼ÀÄ.	MAzÀÄ ¸ÁªÀiÁ£Àå ¨ÁºÀĪÀ£ÀÄß ºÉÆA¢gÀĪÀ JgÀqÀÄ PÉÆãÀUÀ¼ÀÄ
C©üªÀÄÄR (opposite) PÉÆãÀUÀ¼ÀÄ	MAzÀÄ ¸ÁªÀiÁ£Àå ¨ÁºÀĪÀ£ÀÄß ºÉÆA¢®èzÀ JgÀqÀÄ PÉÆãÀUÀ¼ÀÄ

¥Á±Àéð ¨ÁºÀÄUÀ¼ÀÄ ( ¸ÁªÀiÁ£Àå ±ÀÈAUÀ EzÉ)	C©üªÀÄÄR ¨ÁºÀÄUÀ¼ÀÄ ( ¸ÁªÀiÁ£Àå ±ÀÈAUÀ E®è)	C£ÀÄPÀæªÀÄ PÉÆãÀUÀ¼ÀÄ (¸ÁªÀiÁ£Àå ¨ÁºÀÄ EzÉ)	C©üªÀÄÄR PÉÆãÀUÀ¼ÀÄ (¸ÁªÀiÁ£Àå ¨ÁºÀÄ E®è)
(AB,BC) : B ¸ÁªÀiÁ£Àå ±ÀÈAUÀ (BC,CD) : C ¸ÁªÀiÁ£Àå ±ÀÈAUÀ (CD,DA) : D ¸ÁªÀiÁ£Àå ±ÀÈAUÀ (DA,AB) : A ¸ÁªÀiÁ£Àå ±ÀÈAUÀ	(AB,CD) (AD,BC)	( ABC, BCD) : BC ¸ÁªÀiÁ£Àå ¨ÁºÀÄ ( BCD, CDA) : CD ¸ÁªÀiÁ£Àå ¨ÁºÀÄ ( CDA, DAB) : DA ¸ÁªÀiÁ£Àå ¨ÁºÀÄ ( DAB, ABC) : AB ¸ÁªÀiÁ£Àå ¨ÁºÀÄ	(ABC, ADC) (BAD , BCD)

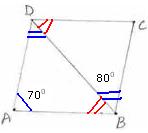
MAzÀÄ ZÀvÀĨsÀÄðdzÀ £Á®ÄÌ M¼ÀPÉÆãÀUÀ¼À ªÉÆvÀÛ 360⁰  EgÀÄvÀÛzÉ. EzÀ£Àß UÀtÂvÀ ±Á¸ÀÛçzÀ ¥ÀæPÁgÀ ¸Á¢ü¸À§ºÀÄzÉ?

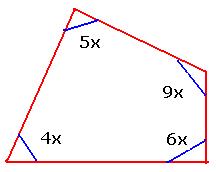
6.7.1 ¸ÀªÀĸÉå1: MAzÀÄ ZÀvÀĨsÀÄðdzÀ £Á®ÄÌ PÉÆãÀUÀ¼ÀÄ 4:5:6:9. C£ÀÄ¥ÁvÀzÀ°èªÉ. D PÉÆãÀUÀ¼ÀÄ£ÀÄß PÀAqÀÄ»r¬Äj.

¥ÀjºÁgÀ:

MAzÀÄ ZÀvÀĨsÀÄðdzÀ £Á®ÄÌ PÉÆãÀUÀ¼À ªÉÆvÀÛ = 360^0 PÉÆãÀUÀ¼À C£ÀÄ¥ÁvÀ = 4:5:6:9 D PÉÆãÀUÀ¼À ¥ÀjªÀiÁt = 4x, 5x, 6x, 9xDVgÀ°. £Á®ÄÌ PÉÆãÀUÀ¼À ªÉÆvÀÛ = 4x+5x+6x+9x = 360^0: 24x = 360^0: x = 360/24 = 15^0 1£Éà PÉÆãÀ = 4x = 4*15 = 60^0,2£Éà PÉÆãÀ = 5x = 5*15 =75^0 3£Éà PÉÆãÀ = 6x = 6*15 =90^0,4£Éà PÉÆãÀ = 9x= 9*15 = 135^0 ZÀvÀĨsÀÄðdzÀ £Á®ÄÌ PÉÆãÀUÀ¼ÀÄ = 60^0, 75^0, 90^0 ªÀÄvÀÄÛ 135^0.

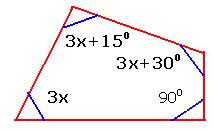
6.7.1 ¸ÀªÀĸÉå 2: MAzÀÄ ZÀvÀĨsÀÄðdzÀ PÉÆãÀUÀ¼ÀÄ: 3x, 3x+15⁰, 3x+30⁰ ªÀÄvÀÄ 90⁰ DzÀgÉ J¯Áè PÉÆãÀUÀ¼À£ÀÄß PÀAqÀÄ»r.

¥ÀjºÁgÀ:

ZÀvÀĨsÀÄðdzÀ £Á®ÄÌ PÉÆãÀUÀ¼À ªÉÆvÀÛ = 360^0 3x+3x+15^0+3x+30^0+90^0 = 360^0 9x+135^0=360^0 9x=225^0 x= 25^0 1£Éà PÉÆãÀ 3x = 75^0, ,2£Éà PÉÆãÀ 3x+15^0 =75^0+15^0=90^0 3£Éà PÉÆãÀ, 3x+30^0 = 105^0,£Á®Ì£Éà PÉÆãÀ = 90^0(zÀvÀÛ) F £Á®ÄÌ PÉÆãÀUÀ¼À ªÉÆvÀÛ 360^0DVzÉAiÉÄà JAzÀÄ ¥ÀjÃQë¹.

£Á«ÃUÁUÀ¯Éà w½¢gÀĪÀAvÉ MAzÀÄ wæ¨sÀÄdzÀ°è DgÀÄ CA±ÀUÀ½ªÉ. (3 ¨ÁºÀÄUÀ¼ÀÄ ªÀÄvÀÄÛ 3 PÉÆãÀUÀ¼ÀÄ). MAzÀÄ wæ¨sÀÄdªÀ£ÀÄß ¤TgÀªÁV gÀa¸À®Ä

(3 ¨ÁºÀÄUÀ¼ÀÄ CxÀªÁ 2 ¨ÁºÀÄUÀ¼ÀÄ ªÀÄvÀÄÛ 1 PÉÆãÀ CxÀªÁ 1 ¨ÁºÀÄ ªÀÄvÀÄÛ 2 PÉÆãÀUÀ¼ÀÄ) EªÀÅUÀ¼À C¼ÀvÉUÀ¼ÀÄ ¸ÁPÀÄ JA§ÄzÀ£ÀÄß w½¢zÉÝêÉ(¥ÁoÀ 6.4.3)

[3 PÉÆãÀUÀ¼À£ÀÄß ªÀiÁvÀæ ¤ÃrzÁUÀ MAzÀÄ ¤¢ðµÀÖ wæ¨sÀÄd gÀa¸À®Ä ¸ÁzsÀå«®èè.]

wæ¨sÀÄdUÀ½UÉ ºÉÆð¹zÁUÀ MAzÀÄ ZÀvÀĨsÀÄðdzÀ°è 10 CA±ÀUÀ½ªÉ(4 ¨ÁºÀÄUÀ¼ÀÄ, 4 PÉÆãÀUÀ¼ÀÄ, 2 PÀtðUÀ¼ÀÄ). ºÁUÁzÀgÉ MAzÀÄ ZÀvÀĨsÀÄðd gÀa¸À®Ä J¯Áè 10 CA±ÀUÀ¼ÀÄ ¨ÉÃPÉÃ? §gÉà 4 CA±ÀUÀ½AzÀ MAzÀÄ ¤¢ðµÀÖ ZÀvÀĨsÀÄðdªÀ£Àß gÀa¸À®Ä ¸ÁzsÀå«®è. MAzÀÄ ZÀvÀĨsÀÄðdªÀ£Àß ¤TgÀªÁV gÀa¸À®Ä PÀ¤µÀ× 5 CA±ÀUÀ¼ÀÄ ¨ÉÃPÀÄ. (CªÀÅUÀ¼À°è PÀ¤µÀ× JgÀqÀÄ ¨ÁºÀÄUÀ¼ÀÄ EgÀ¯Éà ¨ÉÃPÀÄ)

6.7.1 vÀBSÉÛ1:

¸ÀA.	zÀvÀÛ ¨ÁºÀÄUÀ¼ÀÄ	zÀvÀÛ PÀtðUÀ¼ÀÄ	zÀvÀÛ PÉÆãÀUÀ¼ÀÄ	MlÄÖ ¨ÉÃPÁzÀ CA±ÀUÀ¼ÀÄ
1	2	2	1	5
2	2	1	2	5
3	4	1	-	5
4	4	-	1	5
5	3	-	2(CAvÀUÀðvÀ)	5
6	3	2	-	5
7	2(¥Á±Àéð)	-	3	5

ZÀvÀĨsÀÄðdªÀ£ÀÄß gÀa¸ÀĪÀ PÀæªÀÄ(General method for construction of quadrilateral):

(ªÉÄð£À vÀBSÉÛAiÀÄ°è PÉÆlÖAvÉ AiÀiÁªÀÅzÉà CA±ÀzÀ C¼ÀvÉ PÉÆmÁÖUÀ®Æ, ZÀvÀĨsÀÄðdUÀ¼À gÀZÀ£ÉAiÀÄ ¸ÁªÀiÁ£Àå PÀæªÀÄ MAzÉà DVgÀÄvÀÛzÉ.)

UÀªÀĤ¹:

a) MAzÀÄ ¨ÁºÀĪÀ£ÀÄß J¼ÉAiÀÄĪÀ PÀæªÀÄ:

ªÉÆzÀ®Ä MAzÀÄ ¸ÀgÀ¼À gÉÃSÉAiÀÄ£É߼ɬÄj. CzÀgÀ°è MAzÀÄ ©AzÀĪÀ£ÀÄß UÀÄgÀÄw¹. F ©AzÀĪÀ£ÀÄß PÉÃAzÀæªÁVlÄÖPÉÆAqÀÄ, zÀvÀÛ ¨ÁºÀÄ«£À C¼ÀvÉAiÀÄ wædå¢AzÀ F gÉÃSÉAiÀÄ£Àß PÀrzÀÄ, D ¨ÁºÀĪÀ£Àß ¥ÀqɬÄj.

b) PÉÆãÀUÀ¼À£Àß gÀa¸ÀĪÁUÀ PÉÆãÀ ªÀiÁ¥ÀðPÀªÀ£Àß G¥ÀAiÉÆÃV¹j.

c) AiÀiÁªÀÅzÉà DPÀÈwAiÀÄ£ÀÄß gÀa¸ÀĪÁUÀ C£ÀĸÀj¸À¨ÉÃPÁzÀ PÀæªÀÄ.

ºÀAvÀ1: ªÉÆzÀ® zÀvÁÛA±ÀUÀ¼À£ÀÄß ¸ÀÆa¸ÀĪÀ PÀgÀqÀÄ avÀæªÀ£ÀÄß §gɬÄj.

ºÀAvÀ 2: ¨ÉÃPÁzÀ ¨ÁºÀÄUÀ¼ÀÄ ªÀÄvÀÄÛ PÉÆãÀUÀ¼À£Àß ¥ÀqÉAiÀÄ®Ä ªÉÄÃ¯É w½¹zÀ(a,b) PÀæªÀĪÀ£ÀÄß C£ÀĸÀj¹.

1. JgÀqÀÄ ¨ÁºÀÄUÀ¼ÀÄ, JgÀqÀÄ PÀtðUÀ¼ÀÄ ªÀÄvÀÄÛ MAzÀÄ PÉÆãÀªÀ£ÀÄß PÉÆmÁÖUÀ ZÀvÀĨsÀÄðdzÀ gÀZÀ£É:-

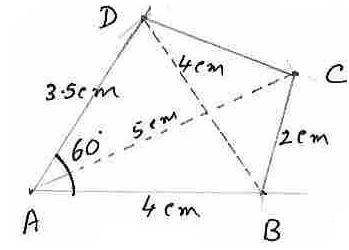
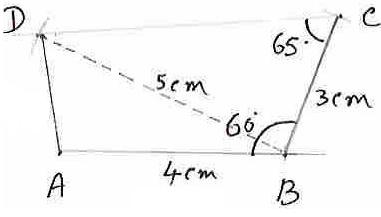
6.7.1 ¸ÀªÀĸÉå 3: AB=4¸ÉA.«Ä., BC=2¸ÉA.«Ä., AC=5¸ÉA.«Ä., BD=4¸ÉA.«Ä., DAB= 60⁰ EgÀĪÀAvÉ ABCD ZÀvÀĨsÀÄðdªÀ£ÀÄß gÀa¹.

ªÉÆzÀ®Ä MAzÀÄ PÀgÀqÀÄ avÀæªÀ£ÀÄß gÀa¹j.

1. A ©AzÀĪÀ£Àß UÀÄgÀÄw¹, EzÀgÀªÀÄÆ®PÀ MAzÀÄ ¸ÀgÀ¼ÀgÉÃSÉAiÀÄ£É߼ɬÄj. 2. AAiÀÄ£Àß PÉÃAzÀæªÁVlÄÖPÉÆAqÀÄ 4 ¸ÉA.«Ä. wædå¢AzÀ F gÉÃSÉAiÀÄ£Àß bÉâ¹.F ©AzÀĪÉà B (AB=4¸ÉA.«Ä.) 3. BAiÀÄ£Àß PÉÃAzÀæªÁVlÄÖPÉÆAqÀÄ 2 ¸ÉA.«Ä.wædå¢AzÀ MAzÀÄ PÀA¸ÀªÀ£É߼ɬÄj. 4. AAiÀÄ£Àß PÉÃAzÀæªÁVlÄÖPÉÆAqÀÄ 5 ¸ÉA.«Ä. wædå¢AzÀ ªÉÄð£À PÀA¸ÀªÀ£Àß C AiÀÄ°è bÉâ¸ÀĪÀAvÉ MAzÀÄ PÀA¸ÀªÀ£É߼ɬÄj. (AC=5¸ÉA.«Ä.,BC=2¸ÉA.«Ä.) 5. AAiÀÄ°è AB AiÀÄ eÉÆvÉ 60^0 PÉÆãÀªÁUÀĪÀAvÉ MAzÀÄ gÉÃSÉAiÀÄ£É߼ɬÄj. 6. B ¬ÄAzÀ, 4¸ÉA.«Ä. wædå¢AzÀ ªÉÄð£À gÉÃSÉAiÀÄ£Àß D AiÀÄ°è PÀrAiÀÄĪÀAvÉ MAzÀÄ PÀA¸ÀªÀ£É߼ɬÄj. (DAB= 60^0, BD=4¸ÉA.«Ä.) DC eÉÆÃr¹. ABCDAiÀÄÄ £ÀªÀÄUÉ ¨ÉÃPÁzÀ ZÀvÀĨsÀÄðd

2. JgÀqÀÄ ¨ÁºÀÄUÀ¼ÀÄ, MAzÀÄ PÀtð ªÀÄvÀÄÛ JgÀqÀÄ PÉÆãÀUÀ¼À£Àß PÉÆmÁÖUÀ ZÀvÀĨsÀÄðdzÀ gÀZÀ£É:

6.7.1 ¸ÀªÀĸÉå 4: AB=4¸ÉA.«Ä., BC=3¸ÉA.«Ä., BD=5¸ÉA.«Ä. ABC= 60⁰, BCD= 65⁰ EgÀĪÀAvÉ ABCD ZÀvÀĨsÀÄðdªÀ£Àß gÀa¹.

ªÉÆzÀ®Ä MAzÀÄ PÀgÀqÀÄ avÀæªÀ£ÀÄß gÀa¹j.

1. A ©AzÀĪÀ£Àß UÀÄgÀÄw¹, EzÀgÀªÀÄÆ®PÀ MAzÀÄ ¸ÀgÀ¼ÀgÉÃSÉAiÀÄ£É߼ɬÄj. 2. AAiÀÄ£Àß PÉÃAzÀæªÁVlÄÖPÉÆAqÀÄ 4 ¸ÉA.«Ä. wædå¢AzÀ F gÉÃSÉAiÀÄ£Àß B AiÀÄ°è PÀrAiÀÄĪÀAvÉ MAzÀÄ PÀA¸ÀªÀ£É߼ɬÄj (AB=4¸ÉA.«Ä.) 3. BAiÀÄ°è ABAiÀÄ eÉÆvÉ 60^0 PÉÆãÀ DUÀĪÀAvÉ MAzÀÄ gÉÃSÉAiÀÄ£É߼ɬÄj. 4. BAiÀÄ£Àß PÉÃAzÀæªÁVlÄÖPÉÆAqÀÄ, 3 ¸ÉA.«Ä. wædå¢AzÀ ªÉÄð£À gÉÃSÉAiÀÄ£Àß  CAiÀÄ°è PÀrAiÀÄĪÀAvÉ MAzÀÄ PÀA¸ÀªÀ£É߼ɬÄj. (BC=3¸ÉA.«Ä., ABC=60^0) 5. C ©AzÀÄ«£À°è BCAiÀÄ eÉÆvÉ 65^0 PÉÆãÀ DUÀĪÀAvÉ MAzÀÄ gÉÃSÉAiÀÄ£É߼ɬÄj. 6. BAiÀÄ£Àß PÉÃAzÀæªÁVlÄÖPÉÆAqÀÄ, 5 ¸ÉA.«Ä. wædå¢AzÀ ªÉÄð£À gÉÃSÉAiÀÄ£Àß D AiÀÄ°è PÀrAiÀÄĪÀAvÉ MAzÀÄ PÀA¸ÀªÀ£É߼ɬÄj. (BD=5¸ÉA.«Ä. (DAB= 60^0, BD=4¸ÉA.«Ä.) DC eÉÆÃr¹ ABCDAiÀÄÄ £ÀªÀÄUÉ ¨ÉÃPÁzÀ ZÀvÀĨsÀÄðd.

3. £Á®ÄÌ ¨ÁºÀÄUÀ¼ÀÄ, MAzÀÄ PÉÆãÀªÀ£Àß PÉÆmÁÖUÀ ZÀvÀĨsÀÄðdzÀ gÀZÀ£É:-

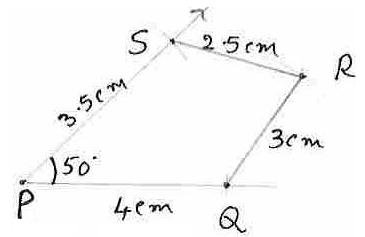
6.7.1 ¸ÀªÀĸÉå5: PQ=4 ¸ÉA.«Ä., QR=3 ¸ÉA.«Ä., RS=2.5 ¸ÉA.«Ä., PS=3.5 ¸ÉA.«Ä., SPQ= 50⁰ EgÀĪÀAvÉ PQRS ZÀvÀĨsÀÄðdªÀ£Àß gÀa¹.

ªÉÆzÀ®Ä MAzÀÄ PÀgÀqÀÄ avÀæªÀ£Àß gÀa¹.

1. P ©AzÀĪÀ£Àß UÀÄgÀÄw¹ MAzÀÄ ¸ÀgÀ¼À gÉÃSÉAiÀÄ£Àß J¼É¬Äj. 2. P ¬ÄAzÀ, 4 ¸ÉA.«Ä. wædå¢AzÀ ªÉÄð£À gÉÃSÉAiÀÄ£Àß Q zÀ°è PÀrAiÀÄĪÀAvÉ MAzÀÄ PÀA¸ÀªÀ£É߼ɬÄj (PQ=4¸ÉA.«Ä.) 3. P ©AzÀÄ«£À°è PQ eÉÆvÉ 50^0PÉÆãÀ DUÀĪÀAvÉ MAzÀÄ gÉÃSÉAiÀÄ£É߼ɬÄj. 4. PAiÀÄ£Àß PÉÃAzÀæªÁVlÄÖPÉÆAqÀÄ, 3.5 ¸ÉA.«Ä. wædå¢AzÀ ªÉÄð£À gÉÃSÉAiÀÄ£Àß  S £À°è PÀrAiÀÄĪÀAvÉ MAzÀÄ PÀA¸ÀªÀ£É߼ɬÄj. (PS=3.5¸ÉA.«Ä., SPQ= 50^0) 5. S £Àß PÉÃAzÀæªÁVlÄÖPÉÆAqÀÄ, 2.5 ¸ÉA.«Ä. wædå¢AzÀ MAzÀÄ PÀA¸ÀªÀ£É߼ɬÄj. 6. QªÀ£Àß PÉÃAzÀæªÁVlÄÖPÉÆAqÀÄ 3 ¸ÉA.«Ä. wædå¢AzÀ ªÉÄð£À PÀA¸ÀªÀ£Àß R £À°è PÀrAiÀÄĪÀAvÉ MAzÀÄ PÀA¸ÀªÀ£É߼ɬÄj. (SR=2.5¸ÉA.«Ä.,QR=3¸ÉA.«Ä.) SR ªÀÄvÀÄÛ QRUÀ¼À£Àß eÉÆÃr¹. PQRS £ÀªÀÄUÉ ¨ÉÃPÁzÀ ZÀvÀĨsÀÄðd.

6.7. 1 C¨sÁå¸À: vÀBSÉÛ 6.7.1 gÀ°è 7 jÃwUÀ¼À°è(««zsÀ C¼ÀvÉUÀ¼À£ÀÄß PÉÆmÁÖUÀ) ZÀvÀĨsÀÄðdªÀ£Àß ¤RgÀªÁV gÀa¸À§ºÀÄzÉAzÀÄ ¥ÀnÖ ªÀiÁrzÉÝêÉ. EªÀÅUÀ¼À°è 3 «zsÀªÁV (ºÀ¹gÀÄ §tÚ) gÀa¸ÀĪÀÅzÀÄ ªÉÄð£ÀAwªÉ. E£ÀÄß G½zÀ 4 «zsÀUÀ¼À° è(ºÀ¼À¢ §tÚ) C¼ÀvÉUÀ½UÀ£ÀĸÁgÀªÁV ZÀvÀĨsÀÄðdUÀ¼À£Àß gÀa¹.

6.7.2 wæ¨sÀÄdzÀ «¹ÛÃtð(Area of a Triangle)

¥ÀPÀÌzÀ ABCAiÀÄ avÀæzÀ°è AD, BF, CEUÀ¼ÀÄ BC, AC ªÀÄvÀÄÛ ABUÀ½UÉ C©üªÀÄÄR ±ÀÈAUÀ ©AzÀÄUÀ¼ÁzÀ A,B, CUÀ½AzÀ J¼ÉzÀ ®A§UÀ¼ÀÄ. wææ¨sÀÄdzÀ «¹ÛÃtð =(1/2) ¥ÁzÀ * JvÀÛgÀ (®A¨ÉÆãÀßvÉ) ABCAiÀÄ «¹ÛÃtð = (1/2)BC*AD = (1/2)AC*BF =(1/2)AB*CE F ¸ÀÆvÀæªÀ£Àß 6.8.7gÀ°è ¸Á¢ü¸À°zÉÝêÉ.

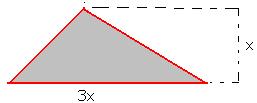
6.7.2 ¸ÀªÀĸÉå 1: MAzÀÄ wæ¨sÀÄeÁPÁgÀzÀ ºÉÆ®zÀ ¥ÁzÀªÀÅ JvÀÛgÀzÀ ªÀÄÆgÀgÀ¶ÖzÉ. C°è ªÀåªÀ¸ÁAiÀÄ ªÀiÁqÀ®Ä 100 ZÀ.«ÄÃmïjUÉ gÀÆ. 36.72 gÀAvÉ

49,572 gÀÆ. RZÁðzÀgÉ, ºÉÆ®zÀ ¥ÁzÀ ªÀÄvÀÄÛ JvÀÛgÀ JµÀÄÖ?

¥ÀjºÁgÀ:

ºÉÆ®zÀ ªÀåªÀ¸ÁAiÀÄ ªÀiÁqÀ®Ä vÀUÀ®ÄªÀ RZÀÄð = gÀÆ.49,572 = ºÉÆ®zÀ «¹ÛÃtð* RZÀÄð(ZÀ.«Ä £À°è) = ºÉÆ®zÀ «¹ÛÃtð*(36.72/100). ºÉÆ®zÀ «¹ÛÃtð = 49572*(100/36.72) = 135000 ZÀ.«Ä. ºÉÆ®zÀ JvÀÛgÀ = x DVgÀ° ¥ÁzÀ= 3x ºÉÆ®zÀ «¹ÛÃtð = (1/2)*¥ÁzÀ*JvÀÛgÀ = (1/2)*3x*x = 3x^2/2 =13500  x^2  =135000*2/3 =90000  x  =300«Ä. ºÉÆ®zÀ JvÀÛgÀ = 300«Ä. : ¥ÁzÀ  = 900«Ä

vÁ¼É £ÉÆÃqÀĪÀÅzÀÄ:

wæ¨sÀÄdzÀ «¹ÛÃtð = (1/2)*900*300 = 900*150 = 135000

ªÀåªÀ¸ÁAiÀÄ RZÀÄð= 135000*(36.72/100) = 49572 zÀvÁÛA±ÀªÉà DVzÉ.

6.7.3 ZÀvÀÄð¨sÀÄðdzÀ «¹ÛÃtð(Area of a quadrilateral)

MAzÀÄ ZÀvÀĨsÀÄðdzÀ PÀtð CzÀ£Àß JgÀqÀÄ wæPÉÆãÀUÀ¼ÁV «¨sÁV¸ÀÄvÀÛzÉ JAzÀÄ £ÀªÀÄUÉ UÉÆwÛzÉ. F ®PÀëtªÀ£Éßà £ÁªÀÅ ZÀvÀĨsÀÄðdzÀ «¹ÛÃtð PÀAqÀÄ»rAiÀÄ®Ä G¥ÀAiÉÆÃV¸ÀÄvÉÛêÉ.

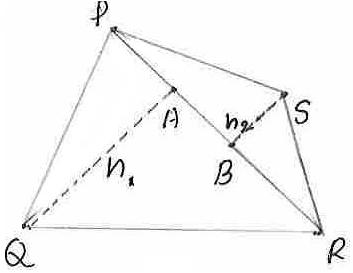
PQRS MAzÀÄ ZÀvÀĨsÀÄðdzÀ PR PÀtðªÀ£É߼ɬÄj. Q¢AzÀ PR UÉ MAzÀÄ ®A§ªÀ£É߼ɬÄj (QA= h1). S¤AzÀ PR UÉ MAzÀÄ ®A§ªÀ£É߼ɬÄj (SB=h2) h1 ªÀÄvÀÄÛ h2 UÀ¼ÀÄ PQR ªÀÄvÀÄÛ PRSUÀ¼À JvÀÛgÀUÀ¼ÀÄ. PQR£À «¹ÛÃtð = ½(¥ÁzÀ *JvÀÛgÀ) =1/2(PR* h1) PRS£À «¹ÛÃtð = ½(¥ÁzÀ *JvÀÛgÀ) = 1/2(PR* h2) ZÀvÀĨsÀÄðd PQRS£À «¹ÛÃtð = PQR£À «¹ÛÃtð + PRS£À «¹ÛÃtð = ½(PR* h1)+ ½(PR* h1) = 1/2*PR* (h1+h2) ZÀzÀgÀ ªÀiÁ£ÀUÀ¼ÀÄ ZÀvÀĨsÀÄðdzÀ «¹ÛÃtð= 1/2 * PÀtð* ¥ÁzÀPÀtðPÉ̼ÉzÀ ®A¨ÉÆãÀßwUÀ¼À ªÉÆvÀÛ

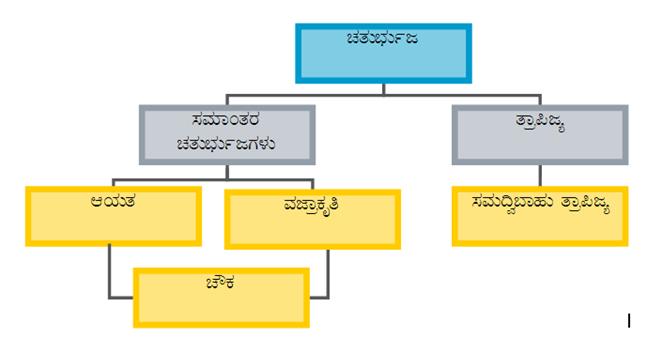
6.7.4 ZÀvÀĨsÀÄðdUÀ¼À «zsÀUÀ¼ÀÄ(Types of quadrilaterals)

«zsÀUÀ¼ÀÄ	ªÀÄÄSå ®PàëtUÀ¼ÀÄ	avÀæ	¨ÁºÀÄUÀ¼ÉƼÀUÉ ¸ÀA§AzsÀ	PÉÆãÀUÀ¼À ¸ÀA§AzsÀ	PÀtðUÀ¼À ¸ÀA§AzsÀ
¸ÀªÀiÁAvÀgÀ ZÀvÀĨsÀÄðd	JgÀqÀÆ dvÉ C©üªÀÄÄR ¨ÁºÀÄUÀ¼ÀÄ ¸ÀªÀiÁAvÀgÀ		1.JgÀqÀÆ dvÉ C©üªÀÄÄR ¨ÁºÀÄUÀ¼ÀÄ ¸ÀªÀiÁAvÀgÀ 2.JgÀqÀÆ dvÉ C©üªÀÄÄR ¨ÁºÀÄUÀ¼ÀÄ ¸ÀªÀÄ.	1.C¨sÀĪÀÄÄR PÉÆãÀUÀ¼ÀÄ ¸ÀªÀÄ. 2. AiÀiÁªÀÅzÉà 2 C£ÀÄPÀæªÀÄ PÉÆãÀUÀ¼À ªÉÆvÀÛ180^0	1.PÀtðªÀÅ ¸ÀªÀiÁAvÀgÀ ZÀvÀĨsÀÄðdªÀ£ÀÄß JgÀqÀÄ ¸ÀªÀð ¸ÀªÀÄ wæPÉÆãÀUÀ¼ÁV «¨sÁV¸ÀÄvÀÛzÉ 2. PÀtðUÀ¼ÀÄ ¥ÀgÀ¸ÀàgÀ C¢üð¸ÀÄvÀÛªÉ.
vÁæ¦då	PÉêÀ® MAzÀÄ eÉÆvÉ C©üªÀÄÄR ¨ÁºÀÄUÀ¼ÀÄ ¸ÀªÀiÁAvÀgÀ		MAzÀÄ eÉÆvÉ C©üªÀÄÄR ¨ÁºÀÄUÀ¼ÀÄ ¸ÀªÀiÁAvÀgÀ	¸ÀªÀiÁAvÀgÀªÀ®èzÀ ¨ÁºÀÄUÀ¼À CAvÀå ©AzÀÄUÀ¼À°è C£ÀÄPÀæªÀĪÁVgÀĪÀ PÉÆãÀUÀ¼ÀÄ ¥Àj¥ÀÇtð
¸ÀªÀÄ¢é¨ÁºÀÄ vÁæ¦då	MAzÀÄ eÉÆvÉ C©üªÀÄÄR ¨ÁºÀÄUÀ¼ÀÄ ¸ÀªÀiÁAvÀgÀ. ¸ÀªÀiÁAvÀgÀ ªÀ®èzÀ ¨ÁºÀÄUÀ¼ÀÄ ¸ÀªÀÄ.		1.MAzÀÄ eÉÆvÉ C©üªÀÄÄR ¨ÁºÀÄUÀ¼ÀÄ ¸ÀªÀiÁAvÀgÀ. 2. ¸ÀªÀiÁAvÀgÀ C®èzÀ ¨ÁºÀÄUÀ¼ÀÄ ¸ÀªÀÄ.	¸ÀªÀiÁAvÀgÀªÀ®èzÀ ¨ÁºÀÄUÀ¼À CAvÀå ©AzÀÄUÀ¼À°è C£ÀÄPÀæªÀĪÁVgÀĪÀ PÉÆãÀUÀ¼ÀÄ ¥Àj¥ÀÇtð. ¸ÀªÀiÁAvÀgÀ ¨ÁºÀÄUÀ¼À CAvÀå ©AzÀÄUÀ¼À°è C£ÀÄPÀæªÀĪÁVgÀĪÀ PÉÆãÀUÀ¼ÀÄ ¸ÀªÀÄ.	PÀtðUÀ¼ÀÄ ¸ÀªÀð¸ÀªÀÄ.
DAiÀÄvÀ	JgÀqÀÆ eÉÆvÉ C©üªÀÄÄR ¨ÁºÀÄUÀ¼ÀÄ ¸ÀªÀiÁAvÀgÀ J¯Áè PÉÆãÀUÀ¼ÀÄ ®A§ PÉÆãÀUÀ¼ÀÄ		1. C©üªÀÄÄR ¨ÁºÀÄUÀ¼ÀÄ ¸ÀªÀÄ. 2. C©üªÀÄÄR ¨ÁºÀÄUÀ¼ÀÄ ¸ÀªÀiÁAvÀgÀ.	J¯Áè PÉÆãÀUÀ¼ÀÄ ¸ÀªÀĪÁVzÀÄÝ ®A§ PÉÆãÀUÀ¼ÁVgÀÄvÀÛªÉ.	1.PÀtðªÀÅ DAiÀÄvÀªÀ£ÀÄß JgÀqÀÄ ¸ÀªÀð ¸ÀªÀð¸ÀªÀÄ wæPÉÆãÀUÀ¼ÁV «¨sÁV¸ÀÄvÀÛªÉ. 2. PÀtðUÀ¼ÀÄ ¸ÀªÀÄ. 3. PÀtðUÀ¼ÀÄ ¥ÀgÀ¸ÀàgÀ C¢üð¸ÀÄvÀÛªÉ.
ªÀeÁæPÀÈw	J¯Áè ¨ÁºÀÄUÀ¼ÀÄ ¸ÀªÀÄ. JgÀqÀÆ eÉÆvÉ C©üªÀÄÄR ¨ÁºÀÄUÀ¼ÀÄ ¸ÀªÀiÁAvÀgÀ		1.J¯Áè ¨ÁºÀÄUÀ¼ÀÄ ¸ÀªÀÄ. 2.  JgÀqÀÆ eÉÆvÉ C©üªÀÄÄR ¨ÁºÀÄUÀ¼ÀÄ ¸ÀªÀiÁAvÀgÀ.	1. C©üªÀÄÄR PÉÆãÀUÀ¼ÀÄ ¸ÀªÀð¸ÀªÀÄ. 2. AiÀiÁªÀÅzÉà 2 C£ÀÄPÀæªÀÄ PÉÆãÀUÀ¼À ªÉÆvÀÛ 180^0	1.PÀtðUÀ¼ÀÄ ªÀeÁæPÀÈwAiÀÄ£ÀÄß 2 ¸ÀªÀð¸ÀªÀÄ wæPÉÆãÀUÀ¼ÁV «¨sÁV¸ÀÄvÀÛªÉ. 3. PÀtðUÀ¼ÀÄ ¥ÀgÀ¸ÀàgÀ ®A§ªÁV C¢üð¸ÀÄvÀÛªÉ.
ZËPÀ	J¯Áè ¨ÁºÀÄUÀ¼ÀÄ ¸ÀªÀÄ ªÀÄvÀÄÛ J¯Áè PÉÆãÀUÀ¼ÀÄ ®A§PÉÆãÀUÀ¼ÀÄ		1.J¯Áè ¨ÁºÀÄUÀ¼ÀÄ ¸ÀªÀÄ. 2.  JgÀqÀÆ eÉÆvÉ C©üªÀÄÄR ¨ÁºÀÄUÀ¼ÀÄ ¸ÀªÀiÁAvÀgÀ.	J¯Áè PÉÆãÀUÀ¼ÀÄ ¸ÀªÀĪÁVzÀÄÝ ®A§PÉÆãÀUÀ¼ÁVgÀÄvÀÛªÉ.	1.PÀtðUÀ¼ÀÄ ZËPÀªÀ£Àß JgÀqÀÄ ¸ÀªÀð¸ÀªÀÄ wæPÉÆãÀUÀ¼ÁV «¨ÁV¸ÀÄvÀÛªÉ. 2. PÀtðUÀ¼ÀÄ ¸ÀªÀÄ. 3. PÀtðUÀ¼ÀÄ ¥ÀgÀ¸ÀàgÀ ®A§ªÁV C¢üð¸ÀÄvÀÛªÉ.

ZÀvÀĨsÀÄðdUÀ¼À ¥ÀjªÁgÀ £ÀPÉëAiÀÄ£ÀÄß F PɼÀV£ÀAvÉ ¸ÀÆa¸À§ºÀÄzÀÄ:

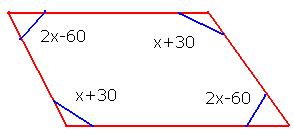
6.7.4 ¸ÀªÀĸÉå 1: MAzÀÄ ¸ÀªÀiÁAvÀgÀ ZÀvÀĨsÀÄðdzÀ C£ÀÄPÀæªÀÄ JgÀqÀÄ PÉÆãÀUÀ¼ÀÄ, (x+30) ªÀÄvÀÄÛ (2x-60) DVªÉ. ºÁUÁzÀgÉ D ¸ÀªÀiÁAvÀgÀ ZÀvÀĨsÀÄðdzÀ J¯Áè PÉÆãÀUÀ¼À£ÀÄß PÀAqÀÄ»r¬Äj.

¥ÀjºÁgÀ:

¸ÀªÀiÁAvÀgÀ ZÀvÀĨsÀÄðdzÀ AiÀiÁªÀÅzÉà JgÀqÀÄ C£ÀÄPÀæªÀÄ PÉÆãÀUÀ¼À ªÉÆvÀÛ =180^0 (x+30)+(2x-60) = 180^0 {(x+30) ªÀÄvÀÄÛ (2x-60) JgÀqÀÄ C£ÀÄPÀæªÀÄ PÉÆãÀUÀ¼ÀÄ} 3x-30 = 180^0 x =70^0 D PÉÆãÀUÀ¼ÀÄ: x+30 = 100^0 ªÀÄvÀÄÛ 2x-60 = 80^0 ¸ÀªÀiÁAvÀgÀ ZÀvÀĨsÀÄðdzÀ°è C©üªÀÄÄR PÉÆãÀUÀ¼ÀÄ ¸ÀªÀð¸ÀªÀÄ. G½zÉgÀqÀÄ PÉÆãÀUÀ¼ÀÄ100^0 ªÀÄvÀÄÛ 80^0. £Á®ÄÌ PÉÆãÀUÀ¼ÀÄ:- 100^0, 80^0, 100^0 ªÀÄvÀÄÛ 80^0

6.7.4 ¸ÀªÀĸÉå 2:   ABCD ¸ÀªÀiÁAvÀgÀ ZÀvÀĨsÀÄðdzÀ°è, DAB= 70⁰, DBC = 80⁰ DzÀgÉCDB ªÀÄvÀÄÛ ABD UÀ¼À£Àß PÀAqÀÄ»r¬Äj.

¥ÀjºÁgÀ:

MAzÀÄ ¸ÀªÀiÁAvÀgÀ ZÀvÀĨsÀÄðdzÀ°è AiÀiÁªÀÅzÉà JgÀqÀÄ C£ÀÄPÀæªÀÄ PÉÆãÀUÀ¼À ªÉÆvÀÛ 180^0. BAD + ABD+DBC = 180^0:70^0+ABD+80^0 = 180^0 ABD = 180^0-70^0-80^0 =30^0 BA || CD, ¥ÀAiÀiÁðAiÀÄ PÉÆãÀUÀ¼ÀÄ ¸ÀªÀÄ.                             CDB = ABD ªÀÄvÀÄÛ ADB =DBC CDB = 30^0, ADB = 80^0 ABC = ABD+DBC = 30^0+80^0 =110^0 ¸ÀªÀiÁAvÀgÀ ZÀvÀĨsÀÄðdzÀ°è C¨sÀĪÀÄÄR PÉÆãÀUÀ¼ÀÄ ¸ÀªÀð¸ÀªÀÄ. BCD = 70^0. £Á®ÄÌ PÉÆãÀUÀ¼ÀÄ:- 70^0, 110^0, 70^0ªÀÄvÀÄÛ 110^0

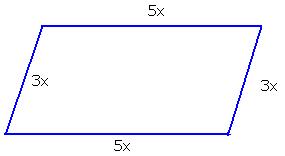
6.7.4 ¸ÀªÀĸÉå 3: MAzÀÄ ¸ÀªÀiÁAvÀgÀ ZÀvÀĨsÀÄðdzÀ JgÀqÀÄ ¨ÁºÀÄUÀ¼ÀÄ 3:5 C£ÀÄ¥ÁvÀzÀ°èªÉ ªÀÄvÀÄÛ ¸ÀÄvÀÛ¼ÀvÉ 48 ¸ÉA.«Ä. DzÀgÉ D ¸ÀªÀiÁAvÀgÀ ZÀvÀĨsÀÄðdzÀ ¨ÁºÀÄUÀ¼À£ÀÄß PÀAqÀÄ»r.

¥ÀjºÁgÀ:

MAzÀÄ ¸ÀªÀiÁAvÀgÀ ZÀvÀĨsÀÄðdzÀ°è,¸ÀÄvÀÛ¼ÀvÉ =  £Á®ÄÌ ¨ÁºÀÄUÀ¼À ªÉÆvÀÛ C£ÀÄPÀæªÀÄ ¨ÁºÀÄUÀ¼À C£ÀÄ¥ÁvÀ = 3:5: D ¨ÁºÀÄUÀ¼ÀÄ 3x ªÀÄvÀÄÛ 5x DVgÀ°   3x+5x+3x+5x = 48: 16x =48  x = 48/16 = 3 3x = 3*3 = 9¸ÉA.«Ä., 5x = 5*3 = 15¸ÉA.«Ä. C£ÀÄPÀæªÀÄ ¨ÁºÀÄUÀ¼ÀÄ : 9¸ÉA.«Ä. ªÀÄvÀÄÛ 15 ¸ÉA.«Ä. ¸ÀªÀiÁAvÀgÀ ZÀvÀĨsÀÄðdzÀ ¨ÁºÀÄUÀ¼ÀÄ 9¸ÉA.«Ä., 15¸ÉA.«Ä., 9 ¸ÉA.«Ä. ªÀÄvÀÄÛ 15¸ÉA.«Ä vÁ¼É: ¸ÀÄvÀÛ¼ÀvÉ = £Á®ÄÌ ¨ÁºÀÄUÀ¼À ªÉÆvÀÛ= 9+15+9+15 = 48 ¸ÉA.«Ä(zÀvÁÛA±À)

6.7 PÀ°vÀ ªÀÄÄSÁåA±ÀUÀ¼ÀÄ

PÀæ.¸ÀA.	£É£À¦qÀ¨ÉÃPÁzÀ CA±ÀUÀ¼ÀÄ
1	ZÀvÀĨsÀÄðdzÀ «¹ÛÃtð= 1/2 * PÀtð * ¥ÁzÀ PÀtðPÉ̼ÉzÀ ®A¨ÉÆãÀßwUÀ¼À ªÉÆvÀÛ.